基于改進ACO與PSO算法的結構可靠度分析
李彥蒼,恒北北,彭雙紅,程秋月,伴晨光
(河北工程大學土木工程學院,河北邯鄲056038)
可靠度在結構設計中的應用始于20世紀40年代,其核心內容是結構可靠指標的計算。工程中常用的可靠指標計算方法主要有一次二階矩法、JC法、梯度優化法以及響應面法、蒙特卡羅法及隨機有限元等[1-7]。使用這些方法常會遇到很多復雜問題難以解決,如極限狀態曲面難以解析描述,仿真計算量大,難以做到有效搜索解空間來找到標準正態空間原點至極限狀態曲面的最短距離[8]以及最弱失效路徑[9]等問題。近幾年來,計算群體智能算法[10]迅猛發展,其中粒子群算法(Particle Swarm Optimization PSO)和蟻群算法(Ant Colony Optimization ACO)可用在系統設計、多目標優化、模式識別、信號處理、決策制定、工件排序、車輛調度、建設工程等領域[11-17],并表現出在求解組合優化問題上所具有的獨特優勢。
本文通過引入信息熵,優化參數τ,對ACO算法進行改進,進而確定結構失效路徑;再使用PSO算法對結構進行可靠指標的求解。并以十桿桁架為例,分別采用響應面法、改進遺傳算法與本算法對其可靠度指標進行對比分析。
1 基于改進后的ACO的失效路徑的尋找
1.1 ACO 簡介
ACO由一系列模擬現實中蟻群覓食過程的算法組成。以TSP問題為例,設m是蟻群中螞蟻的個數,n為城市數,τij表示t時刻在 i j連線上的信息量,ηij為螞蟻由城市i轉移到城市j的期望信息。初始時刻,各條路徑上的信息量相等。Pkij(t)表示在t時刻螞蟻由位置i轉移到位置j的概率,則
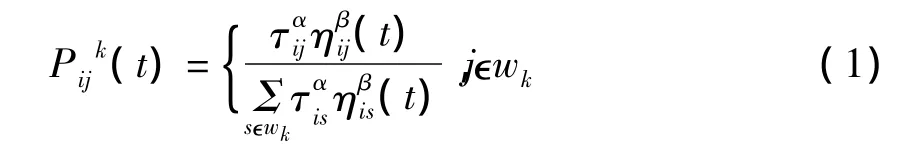
信息素的更新公式為
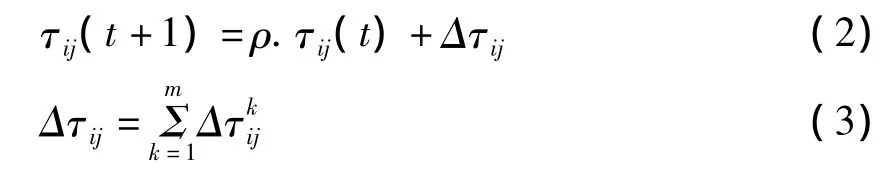
1.2 ACO 改進
為了解決基本蟻群算法的過早收斂問題,采用文獻[18] 方法,即通過引入信息熵H,控制信息熵的值,來改進參數τ,進而對蟻群算法進行改進。開始時每條路徑都會有等量的信息素,信息熵取最大值,隨著信息素的增加,信息熵值逐漸變小,繼續進行容易出現早熟以使算法出現停滯現象,所以此時通過控制與信息熵有關的α(t)和β'(t)的值來控制此時最優路徑出現的區域和信息素更新的范圍,進而避免了早熟和停滯現象的發生,找到最優路徑。
1.3 改進后的ACO尋找最短失效路徑
所謂失效路徑就是由初始結構所處的狀態到結構失效狀態之間的任一條路徑。對于一個結構來說會有多條失效路徑,每條失效路徑又包括多個結構單元。其中最弱失效路徑就是結構單元依次按可靠指標最小失效,直至整個結構體系失效的一條路徑[9]。
對于ACO求解 TSP問題[19],啟發式信息 ηij(d為城市i到城市j的距離),所以當通過改ij進后的蟻群算法尋找結構失效路徑時,可以假設啟發式信息(β為結構單元的可靠指標),螞蟻數為m,結構單元數為n
使用ACO尋找失效路徑的操作步驟如下:
1.初始化參數,τij(0)=0。
2.將m只螞蟻放在n個結構單元上。
3.按公式(1)計算每只螞蟻移動到下一個結構單元的概率,根據概率選擇螞蟻的移動方向。
4.m只螞蟻遍歷n個結構單元后,路徑上的信息素增加。
5.所有路徑信息素按公式(2)(3)更新,進行局部尋優。
6.多次重復(3)-(5)步,進行全局尋優,找出最優路徑。
2 基于PSO的可靠指標計算模型
2.1 PSO 簡介
PSO將每個個體看成搜索空間中的一個沒有體積的粒子,在空間中以一定的速度飛行。對于第i個粒子,它經歷的最好位置為Pbest,記為Pi,在群體中所有粒子經歷過的最好位置為gbest,記為Pg。粒子根據如下公式來更新自己的位置和速度
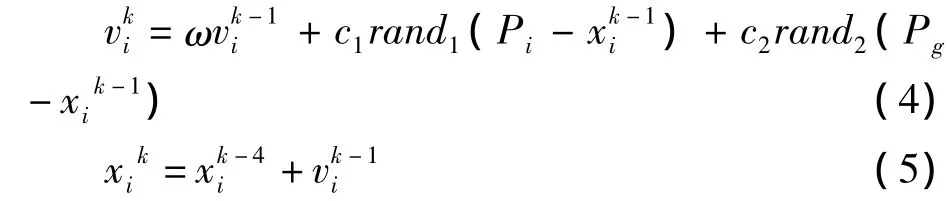
式中,ω-慣性權重;c1和c2-加速度常數;rand1和rand2-兩個在[0,1] 范圍內的隨機函數;-第k次迭代粒子i的飛行速度-第k次迭代粒子i的位置。
2.2 模型建立
在結構可靠度分析中,結構可靠指標β的幾何意義是標準正態空間內,坐標原點到極限狀態曲面的最短距離。
x1,x2,…,xn是結構中的隨機變量,由這些隨機變量組成的極限狀態方為z=g(x1,x2,…,xn)=0。
把β看成極限狀態曲面上點P(x1,x2,…,xn)的函數,通過優化求解,找到β最小值。
約束優化模型:
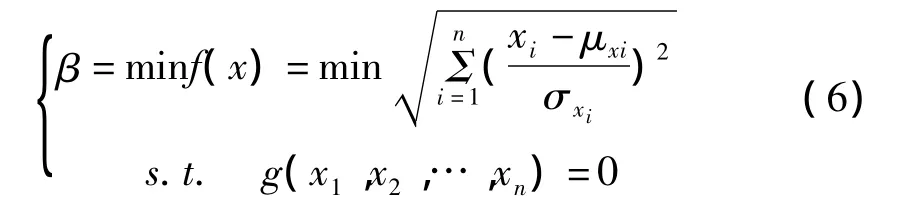
式中,μxi,σxi-隨機變量 xi的均值、標準差。
采用罰函數法將式(6)變成相應的無約束優化問題:
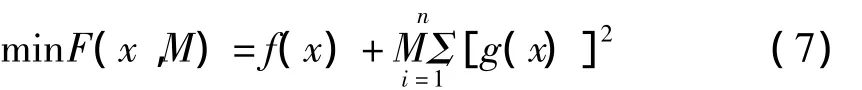
式中,M-相應的罰因子(足夠大的正數),相應的項為罰項。
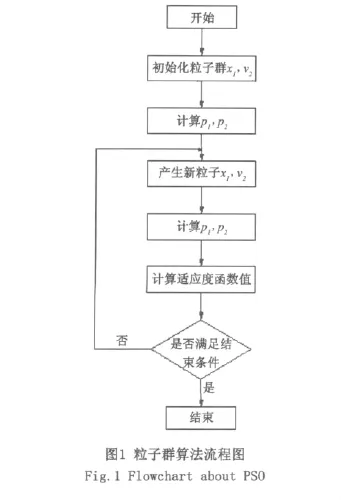
粒子群算法的流程如圖1所示。
3 實例分析
10桿桁架結構如圖2所示,各桿的橫截面積為正態分布的基本變量,均值為6.452×10-3m2,變異系數為 0.05,楊氏模量為 6.895 ×1010pa,施加的荷載為p1=p2=4.45×105N,結構極限狀態函數取為桁架的最大位移不超過最大允許位移為0.101 6m,求此時的可靠度。
首先采用改進的ACO確定結構的失效路徑,進而通過PSO算法對可靠指標進行求解。在求解過程中,每代產生20個粒子數。粒子群算法的迭代收斂過程如圖3所示。圖中表示最優粒子的迭代收斂過程圖,可以看出在第十次迭代過程中最優粒子已經收斂達到最好的精度,隨著進一步迭代全部粒子收斂到最優值。此算法經過十次迭代,得到的可靠指標為0.682 37,相應的設計點坐標為(6.311 0,6.436 6,6.315 0,6.443 6,6.452 6,6.443 6,6.384 5,6.389 0,6.428 4,6.409 5),從文獻[21] 中可以得到響應面法與遺傳算法在計算本結構時的可靠指標及相應的設計點坐標。三種算法計算結果比較見表1。
與響應面法[20]的迭代過程相比,PSO采用較少的粒子數,就能達到較好的計算精度。與遺傳算法[21]相比,PSO算法由于具有強大的全局尋優能力,迭代收斂速度快,對于處理復雜的極限狀態方程問題,具有良好的適用性。
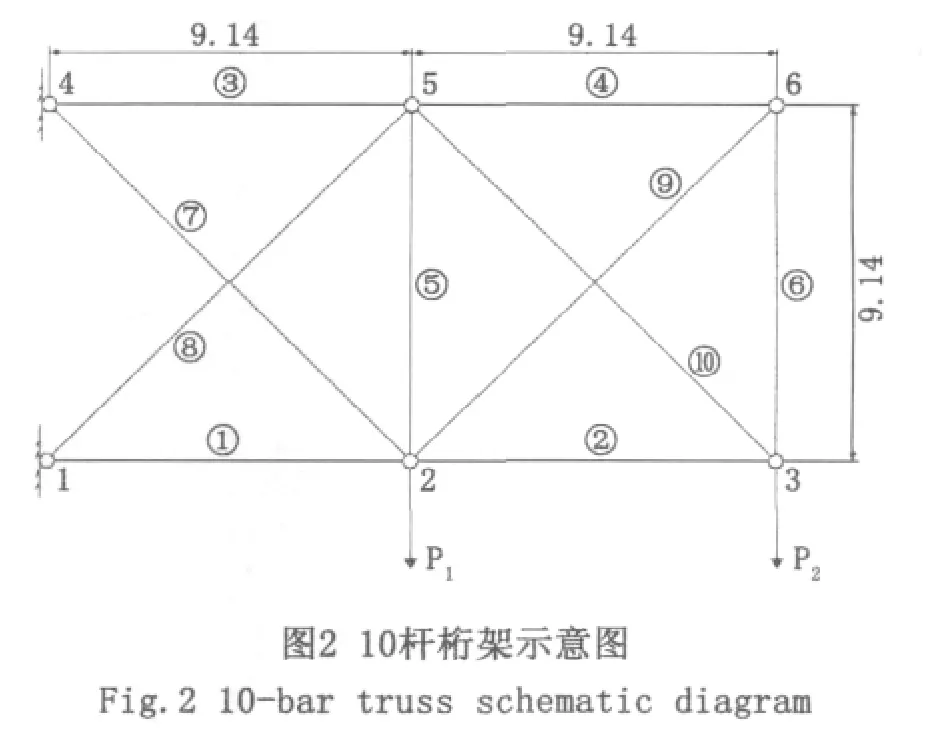
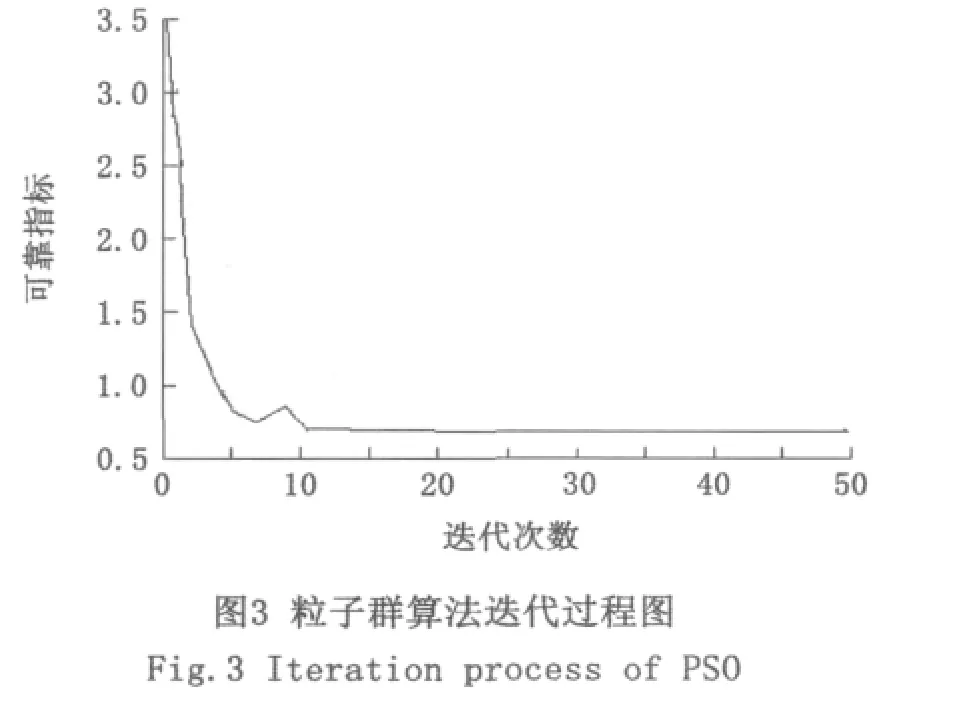

表1 三種算法計算結果比較Tab1.Three algorithms comparison of results
4 結論
1)引入信息熵,對參數 進行調整,避免了ACO的早熟和停滯現象發生,快速的找到最優路徑。
2)在ACO找到最優路徑的情況下,PSO能夠通過較少的粒子數,快速收斂,求出更準確的目標函數值。
[1] MOSES F.System reliability developments in structural engineering[J] .Structural Safety,1982,1(1):3 -13.
[2] 張 明.結構可靠度分析-方法與程序[M] .北京:科學出版社,2009.
[3] 譚海濤,徐定海,王善.一種計算結構可靠度的一元分解法[J] .哈爾濱工程大學學報,2009,30(8):883-886.
[4] 張建仁,許福友.計算結構可靠指標的子域抽樣法[J] .土木工程學報,2003,36(12):39-43.
[5] 周彬彬,顧祥林,張偉平,等.海洋大氣環境下鋼筋混凝土梁受彎時變可靠度分析[J] .土木工程學報,2010:15-21.
[6] 呂大剛,賈明明,李剛.結構可靠度分析的均勻設計響應面法[J] .工程力學,2011,28(7):109-116..
[7] 武清璽.結構可靠性分析及隨機有限元法[M] .北京:機械工業出版社,2005.
[8] 閻宏生,胡云昌,李向京.結構可靠性分析的一種新方法[J] .天津大學學報,2000,33(6):32-35.
[9] 蔡文學,程耿東.災害荷載下彈塑性結構體系可靠度的近似計算[J] .大連理工大學學報,1996,36(1):6-12.
[10] 梁艷春,吳春國,時小虎,等.群智能優化算法理論與應用[M] .北京:科學出版社,2009.
[11] LIU Q,WANG C G.A discrete particles swarm optimization algorithm for rectilinear branch pipe routing[J] .Assembly Automation,2011,31(4):363-368.
[12] 周書敬,潘靖.基于改進蟻群算法的鋼管混凝土構件的優化[J] .河北工程大學學報:自然科學版,2011,28(4):10-13.
[13] MOUSA F M.Particle swarm optimization algorithm for smart antenna system[J] .Journal of Mobile Communication,2011,5(1):6-10.
[14] 趙文紅,張紅斌.一種改進的粒子群優化算法[J] .河北科技大學學報,2006,27(4):317-320.
[15] 李正濤,趙環宇,馬獻果.應用粒子群算法從已知數據中確定置信測度和似然測度[J] .河北科技大學學報,2011,32(2):128-132.
[16] 周書敬,薄 濤,史三元.混合算法在輕鋼結構優化設計中的應用[J] .河北工程大學學報:自然科學版,2011,28(2):71-74.
[17] 張浩,彭曉華,孟宇.基于連續域蟻群改進算法的T-S模型辨識[J] .黑龍江科技學院學報,2007,17(1):74-78.
[18] LI Y C,LI W Q.Adaptive ant colony optimization algorithm based on information entropy:foundation and application[J] .Fundam Inform,2007,77(3):229-242.
[19] YANG J H,SHI X H,MARCHESE M,et al.An ant colony optimization method for generalized TSP problem[J] .Progress in Natural Science,2008,18(11):1417-1422.
[20] 張銀龍,常大民.響應面法用于桁架體系可靠度分析[J] .工程設計CAD與智能建筑,2002(11):57-60.
[21] 魏錦輝,董笑慧,魏保立.遺傳算法及其在結構可靠度計算中的應用[J] .河南科學,2009,27(10):1261-1263.

