AHP-模糊綜合評價法在高職高專學生成績考核指標體系的應用

安 然

（黑龍江建筑職業技術學院，黑龍江 哈爾濱 150025）

AHP-模糊綜合評價法在高職高專學生成績考核指標體系的應用

安 然

（黑龍江建筑職業技術學院，黑龍江 哈爾濱 150025）

鑒于學生成績考核在學生管理中的核心地位，建立系統科學的高職高專學生成績綜合評定方法，綜合考慮定量和定性因素，提高學生成績考核的科學性和準確性具有非常現實的意義.本文建立一個模糊綜合評價體系，對學生成績考核的常見問題進行分析的基礎上，利用層次分析法，運用AHP確定權重，確定考核系數，運用該體系針對學生學習效果發展過程的不同時期設置相關參數對學生學習質量進行測評，構建了一套合理的高職高專學生成績綜合判定的考核指標體系.

遞階層次；層次分析法；考試評價體系

AHP是由著名數學家Thomasl.Satty第一次提出來的，這是一種數學模型矩陣定量與向量定性相結合的評價綜合方法，雖然能保證模型的整體性和合理的表達性，但是AHP在進行綜合評價時，缺乏相對統一的、詳細的指標定向量化方法，然而對于模糊綜合評價法恰恰能夠合理的解決此類難以解答的問題.我們在判斷目標的復雜結構時并且在缺少一定的數據情況下，應該把其他合理的方法把難以定量化的評價影響因素通過兩兩比較，可以將這些影響因素組建為層次結構的數學模型，更加有效地定多因素指標的相對重要程度，進一步進行評價和分析問題模型.

在應用AHP-模糊綜合分析法在分析和解決生活中難以解答的問題時，首先要把問題進行條理化、層次化，然后進行綜合化，構造出一個有層次、有綜合性的數學矩陣模型，在這種模型下，復雜難以解答的問題也會變得簡單化、迎刃而解，所以我們就可以把它們分解成由多元素所組成的模型部分.然后再把這些多元素按不同的數學屬性以及它們之間相互的關系在形成若干的層次.所以問題就變得更加簡單化.

AHP-模糊綜合分析評價法主要包括兩方面內容：（1）每個層次指標權重的確定，（2）根據最低層次各指標的權重和各方案的屬性值對方案作出綜合評價.

1 建立判斷矩陣

1.1（1）根據模糊綜合分析法確定評價方案的指標權重論域： E={e1,e2,…,en}

（2）將AHP-模糊綜合分析法應用在成績中，得出評語等級論域為：U={u1,u2,…,um}

（3）若n≥9就采用遞階結構，為了讓結果更精確我們要一層一層地進行遞進.一般情況下，m取3、5、7、9.這樣就可以得到模糊的綜合的指標,要想使結果達到權向量有公式：

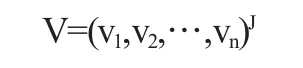
先確定單一準則情況下各指標的相對權重：如下表所示：

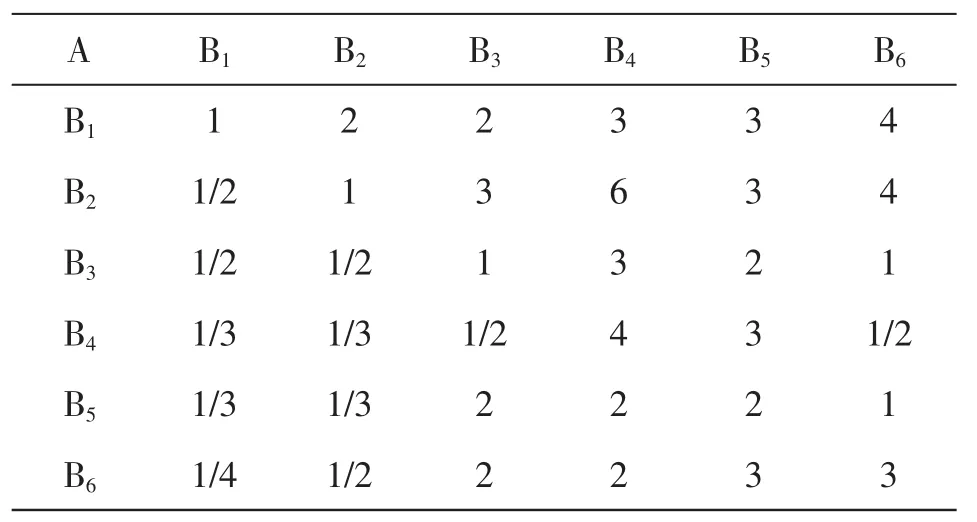
表1

1.2（1）根據計算判斷表格的最大特征λmax=6.139

特征向量:w1=[0.3384,0.2347,0.1295,0.0808,0.1008,0.1158]

對于判斷的表格，統一性數據為：

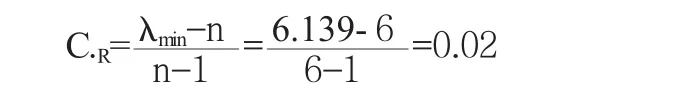
即可得出平均隨機統一性數據RI=1.24統一性比例為：

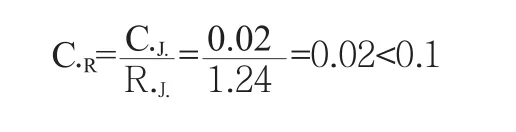
（2）若采用同樣的方法可以得到相對數據w2

（3）建立學生考試考核評價的遞階層次結構——考試評價體系表2

表2 考試評價體系表

（4）合成權重的分析如下表3所示：

同樣對于數據的合成分量也需要進行統一性的檢驗，是否滿足整體統一性的要求.對于特征向量是否能作為向量權重，需要通過整體性檢驗來進行進一步的確定.

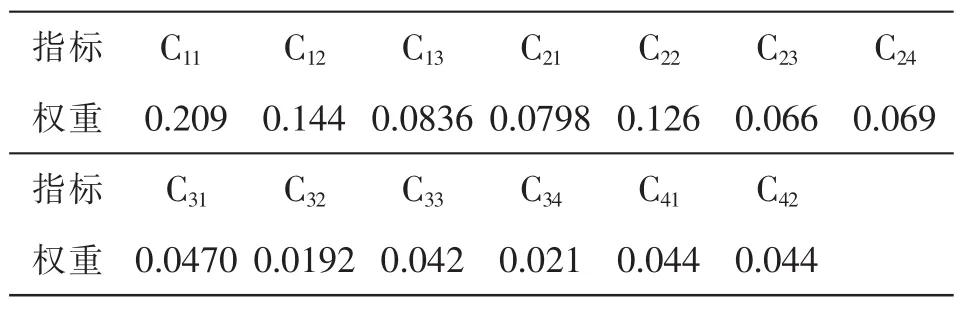
表3

1.3 根據學生的學習成績進行分類時，可以得出一級指標學習的態度、交流的能力以及各種資料應用的能力，還可以得出它們的分類級別，這樣就可以得出模糊綜合評價矩陣分別為：

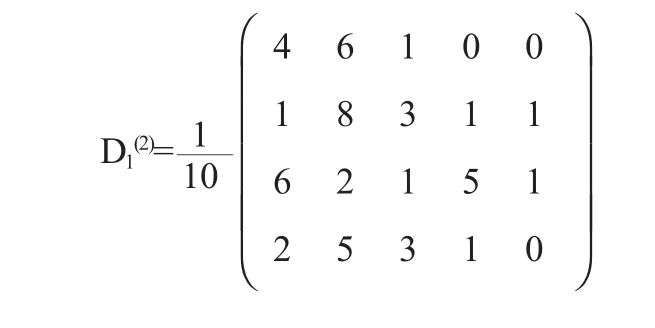
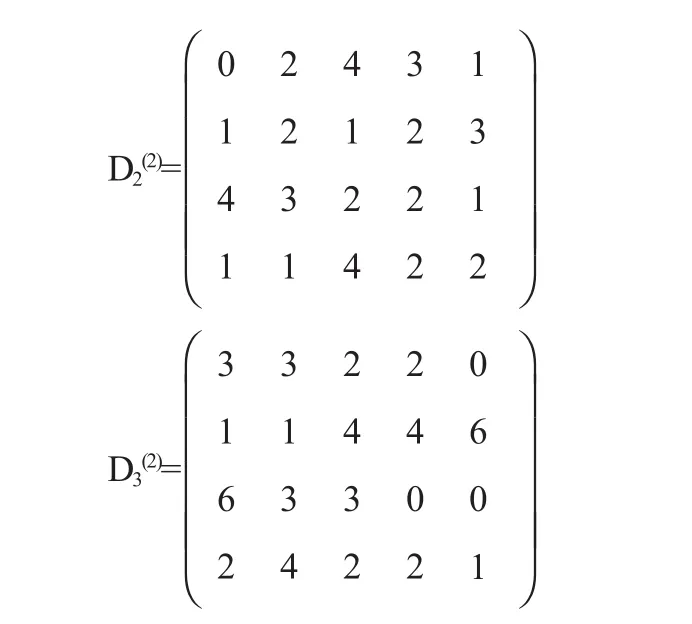
(1)如果我們選用模糊矩陣模型合成運算模型，就應該考慮所有的影響因素，考慮所有的因素必須依據權重的大小.這樣得到的運算模型為：

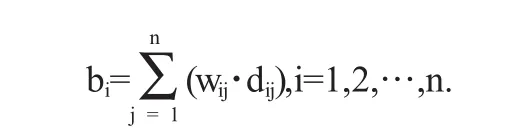
（2）為了更加使學生的各項成績等級有明顯的分類，下面進行舉例：

其中一位學生在“學習態度”方面的模糊綜合評價成績結果集是：

同樣的合成的數學模型也可以寫出它們的權重集，并計算出學生在“學生交流”以及“資源利用”方面的評價結果集分別是:

如果將層次評價得到的單因素評價結果集組合成評價指標的模糊評價矩陣C(1)，即

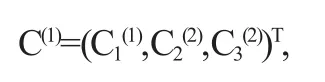
那么評價指標的模糊綜合評價矩陣為：

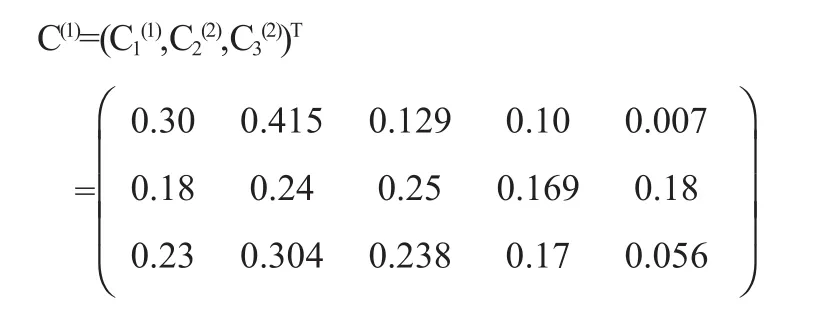
再根據指標的模型權重集W(1)，再采用合成的模糊的運算模型，計算學生學習成績綜合評價的結果權重集為：

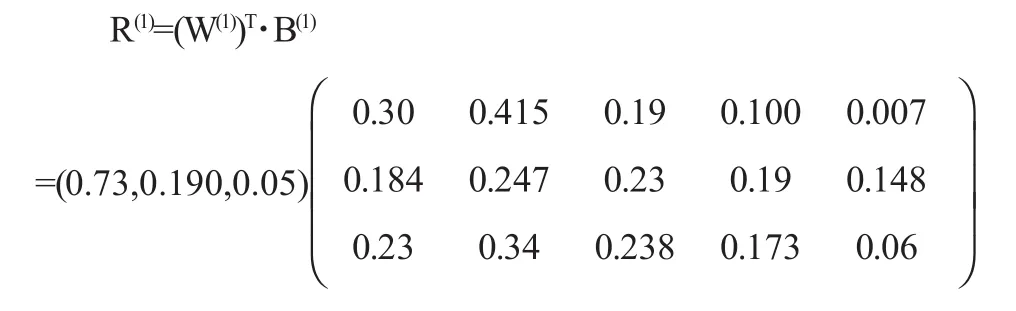
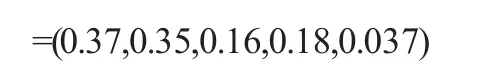
R(1)是指學生成績的綜合模糊模型分析評價的權重結果集，對于評價結果權重集使用的平均法就可以得到學生的綜合評價結果集為：

這就說明了學生所得的成績總分值為82.82分，根據等級的評分級別標準，我們就可以把82.82分的成績的學生在80≤82.82≤90的組值中，那么就屬于“良好”這一個等級.

2 確定判斷矩陣及各層權重

2.1 對于模糊綜合分析法，按照AHP構造判斷矩陣，并計算出其相應的權重值.

如下表4所示：

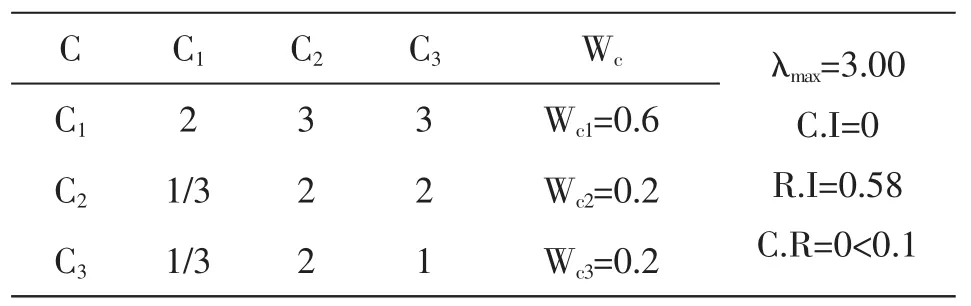
表4

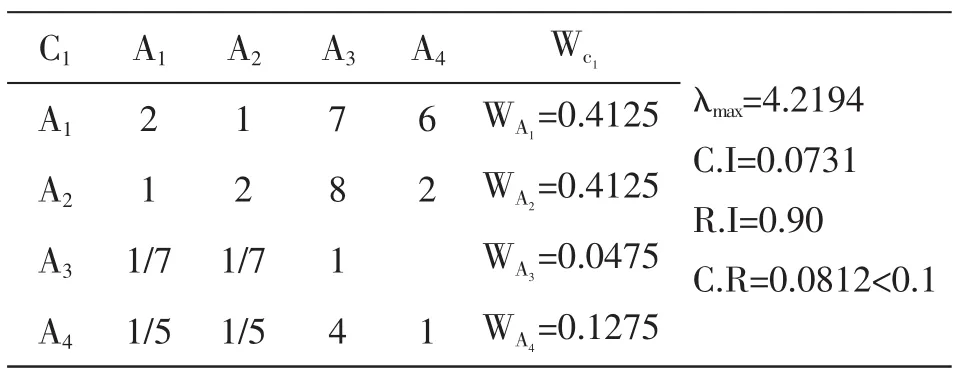
表5

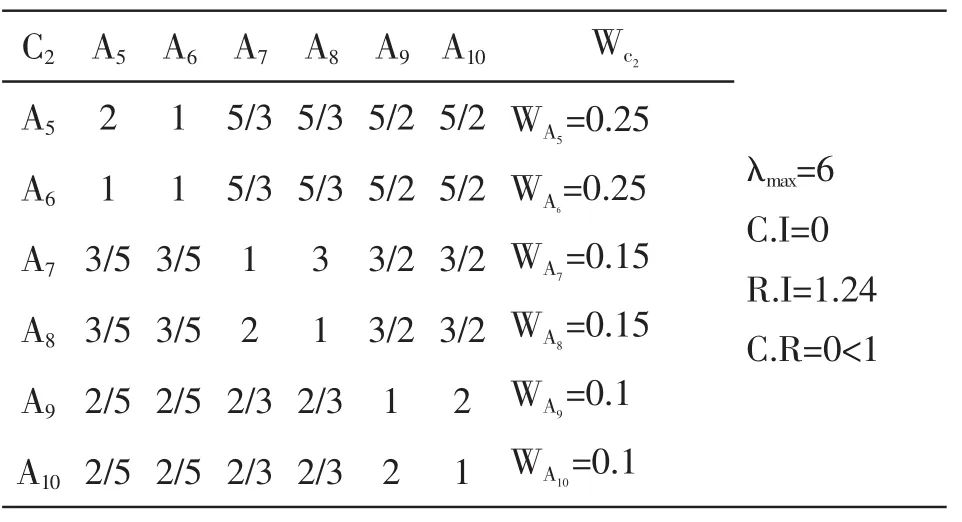
表6

2.2 檢驗一致性及合理的權重

（1）首先檢驗每一層的一致性.

根據以上的各種構造的模糊綜合方法的判斷矩陣，就可以利用積分法和模糊綜合評價法、分析法、計算出各種模糊判斷矩陣的最大特征根值和序權重向量值，與此同時，計算出一致性指標，是否都滿足一致性.

(2)對于總一致性的檢驗和合成權重向量，我們應該需要進一步詳細進行檢驗.

例如：我們以c1作準則的判斷矩陣為：

利用以上的公式可以計算所提出的判斷矩陣，這樣就可以使結果具有綜合的評價的效果，利用模糊綜合評價分析法，使計算過程更加簡便.

3 求解特征值和特征向量

（1）常用的計算方法有：方根、積分.

對于方根度主要步驟如下：

①因為階數低，所以就可以求出最大的特征根，由于檢驗結果是一致性的，這樣就可以得出其他的特征根為0，這樣我們就可以利用兩種方法都可以驗證這一點.

對于不滿足的一致性模型組合的也需要檢驗，檢驗仍應該遵循遞階式的方法，由高層到低層逐層遞階進行，這是因為雖然每層次都得進行一致性檢驗，但是各層對比較判斷矩陣都具有較為滿意的一致性，如果我們考慮模糊綜合分析法在成績中的的影響時，我們就應該把各層的非一致性累積起來，在一起分析和檢驗非一致性.下面我們就一一進行分析.

設B層與Aj相關的影響因素成對比，檢驗判斷在單排序中經一致性，求得單排序一致性指標為CI(j)(j=1,…,m)，求得相應的平均隨機一致性指標RI(j)，(CI(j))RI(j)在層次單排序，這樣我們就可以求B層總排序隨機一致性的比例為：

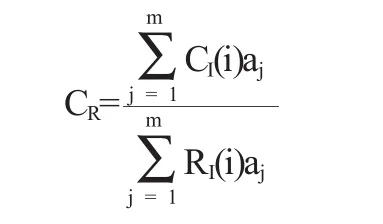
當CR<0.15時，層次總排序結果具有一致性.

當計算平均值時，也不會有太大的偏離.

再著講來，對于實際的構造判斷矩陣，有時也難以考慮到整體的排序的一致性.

對于大多數的實際模糊綜合評價分析方法來說也應該進行一致性的檢驗.

②對于特征根為0時，我們也可以利用模糊綜合分析評價法來驗證這一點：

即單排序一致性指標(CI(j))

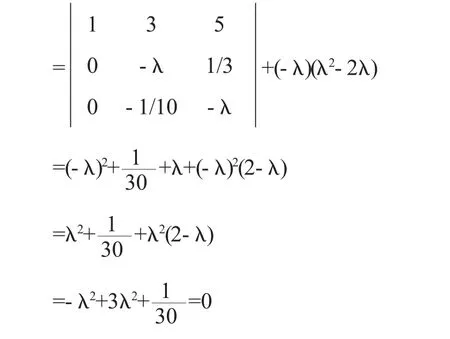
雖然這種判斷矩陣會造成對比較其他的判斷矩陣的辦法減少了其他的因素的影響.不過這一過程，對判斷矩陣的因子影響是很小的.

對于判斷矩陣對應于最大的特征值時的特征向量，經過歸一化為后即為同一層次的相應的因素對于上一層的因素對判斷矩陣的影響.

所以考慮到綜合的全部結果時就應該包含一定程度的非一致性，結果也是和前后結果一致的.

4 對于一致性正反舉證

對于不同的判斷矩陣的屬性，構造的判斷矩陣屬性的矩陣也是不相同的，所以我們應該以優先的權重的向量判斷矩陣為主，并進行一致性檢驗.

根據以上構造的判斷矩陣，利用綜合分析法和積法計算出了各判斷矩陣的最大特征量和單排序權重向量的一致性指標.

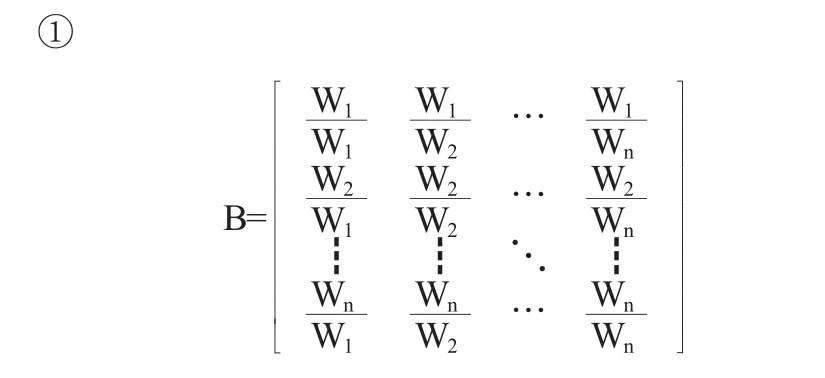
這樣我們就很容易看出，每一行都成比例，因此，判斷矩陣的解就為1，非零的特征值根只有1個.而且，我們還可以得到∑λr=∑aij所以這樣我們還可以得到

即 n=∑λj=λ

②任意兩個比較時，就可以得到相對判斷矩陣的權重精確測度為：

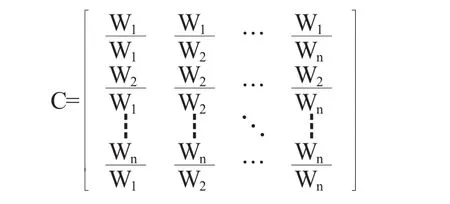
即可得到特征方程的特征根為：|A-KE|=0,其中有一個重實根為λ=n以及n-1重0根.

5 模糊綜合評價法總排序及一致性檢驗

5.1 從上面我們可以得到是一組元素對每一層中的某元素的判斷矩陣權重的向量，由于我們到最后要得到的各元素的一致性檢驗.

尤其是對于那些最低層的方案目標的判斷矩陣的權重的排序向量，進而我們可以得到和進行選擇方案，對于總排序的判斷矩陣權重要從自上而下將權重合成.

設上一層的的層次為（A層），它包含了A1,…,Am一共有m個元素，對于它們的層次的總排序為a1,…,am，這樣還可以設其后的一層次（B層），它包含了n個元素B1,…,Bm.

對于它們關于Aj的層次的總排序單排序判斷矩陣權重的分別為b1j,…,bnj（當Bi與Aj沒有關系時，bij=0）如果想求B層的各元素關于總目標的判斷矩陣權重，即可以求B層的各元素的層次總排序的判斷矩陣的權重b1,…,bn，計算出按下面的方式進行即可得到的是：

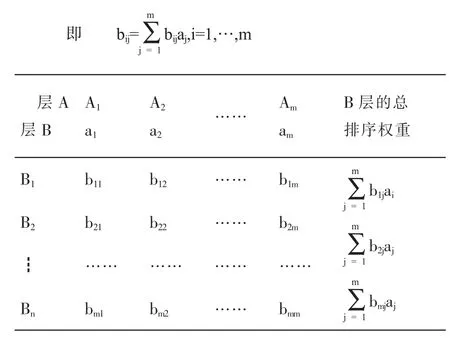
對于相關因素的影響，成對的判斷對于判斷矩陣來說在單排排序中的一致性檢驗.相應的平均判斷矩陣的隨即一致性指標也可以在單排序時求得.

某班60名學生對某學生進行指標評價，評價整理后得到隸屬度矩陣R.

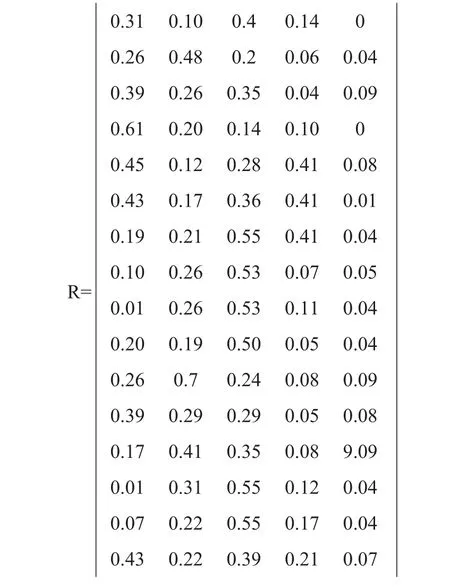
綜合隸屬度X=sR=[0.277,0.254,0.3097,0.0744,0.0323]，即被評價的學生的可能性為30.5%，較好學生的可能性為25.9%.

綜合得分u=DE×ST,DE為評語集E的數值結果，取DE=(100,85,60,55,30)得79.600，即該學生的綜合評價為79.600分.

按照同樣的模型分析法對該班級其余學生也進行相同的評價，所得的結果證明數學模型的有效性和合理性，依據學生的綜合評分就可以進行評選優秀學生.應用AHP-模糊綜合方法的分析方法，在考慮和確定某些因素的影響時，在解決生活中的數學問題時是很好的解決方法.這次我們將AHP和模糊綜合評價相結合，把難以用量化解決的定性判斷化為可操作的重要度的比較，進而建立了學生成績評價模型.

〔1〕吳祈宗.運籌學與最優化方法[M].北京：機械工業出版社，2003.

〔2〕王蓮芬，許樹柏.層次分析法引論[M].北京：中國人民大學出版社，1990.

〔3〕陳曦.大學生初次就業質量評價及影響因素研究[J].華中農業大學，2011（2）.

O29

A

1673-260X（2012）11-0011-05

省教育廳規劃課題（GZC1211035）