冷銣原子樣品中高效靜態(tài)光信號的生成與調(diào)制
張 巖 ,張曉航,張 宇,崔淬礪,國秀珍,2,吳金輝,2
(1.吉林大學(xué) 物理學(xué)院,吉林 長春130012;2.長春理工大學(xué) 光電信息學(xué)院,吉林 長春130012)
1 引 言
隨著全球信息量的爆炸式增長,傳統(tǒng)的以半導(dǎo)體電子學(xué)為基礎(chǔ)的信息技術(shù)已無法滿足人們?nèi)找嬖鲩L的信息需求。為了提高信息處理與傳輸系統(tǒng)的性能,人們開創(chuàng)了全新的光子學(xué)信息技術(shù)[1]。但是光子在非真空中傳輸容易被粒子散射或吸收,且隨著傳輸距離的增加,其損耗也會愈加明顯,對光進行控制和定位也頗有難度。雖然現(xiàn)在已經(jīng)可以通過光纖載波來實現(xiàn)信息的高速傳遞,但若要研制出功能強大的集成光子學(xué)元件還有很多難題。實現(xiàn)低損耗、高保真度的靜態(tài)光信號和光信息存儲,將大大提高量子信息處理的性能和效率,對量子計算、量子通訊、量子密碼、全光網(wǎng)絡(luò)等技術(shù)領(lǐng)域會起到巨大的推動作用[2-3]。
近年來,源于光與物質(zhì)相互作用的原子相干效應(yīng)已經(jīng)成為光信息領(lǐng)域的研究重點,尤其是電磁感應(yīng)光透明( Electromagnetically Induced Transparency,EIT) 現(xiàn)象,由于能夠抑制經(jīng)強耦合激光作用介質(zhì)傳播的弱光信號的吸收并增強透射,大大增加了光信號的傳輸距離,因此基于EIT 現(xiàn)象,利用行波耦合的原子介質(zhì)已被廣泛地應(yīng)用于光速減慢、光信息的相干存儲與反饋[4-6]的研究中。目前,研究人員對相干駐波制備的EIT 機制的研究已獲得了顯著的成果。譬如利用穩(wěn)定的駐波對介質(zhì)介電常數(shù)進行周期調(diào)制,實現(xiàn)了光子帶隙[7-9]和光柵結(jié)構(gòu)[10-11]。若對駐波的強度進行時間調(diào)制,可以使進入介質(zhì)的探測場激發(fā)出前后兩個分量,并耦合成一個群速度為零的靜態(tài)光信號[12-15]。這一機制為光信號處理或光比特控制提供了一個較長時間的非線性作用過程。但是,雙色駐波場耦合作用會導(dǎo)致光學(xué)原子相干和自旋原子相干的一系列高階空間傅里葉分量的激發(fā),使靜態(tài)光快速產(chǎn)生損耗和色散,這一性質(zhì)影響了它的實際應(yīng)用。
為了建立生成高效率、高保真度靜態(tài)光信號的機制,本文采用了一對反向傳播的行波激光場耦合的四能級雙Λ 型冷87Rb 原子樣品作為介質(zhì)進行研究。首先只開啟正向耦合場引導(dǎo)一個正向弱探測光脈沖信號緩慢進入介質(zhì),然后同時絕熱開啟兩個耦合激光場激發(fā)出反向光信號并與正向光信號耦合形成靜態(tài)光信號。在此機制中,因為采用的是單色行波場對原子能級進行耦合,不會激發(fā)出高階原子相干項,從而大大降低了光損耗,提高了靜態(tài)光信號的生成效率和持續(xù)時間。文中還討論了在生成靜態(tài)光信號時對耦合場調(diào)制所需的必要操作條件,最后通過相位調(diào)制法對靜態(tài)光信號進行了處理。
2 理論模型
圖1 表示樣品長度L=3.0 mm,原子密度N=2.0 ×1019m-3的一個冷87Rb 原子系綜的四能級雙Λ 能級結(jié)構(gòu)。本文選取了兩種不同的精細能級結(jié)構(gòu): 能級結(jié)構(gòu)Ⅰ為|5S1/2,F(xiàn)=1〉→|1〉,|5S1/2,F(xiàn)= 2〉→|2〉,|5P1/2,F(xiàn)= 1〉→|3〉和|5P1/2,F(xiàn)=2〉→|4〉; 能級結(jié)構(gòu)Ⅱ為|5S1/2,F(xiàn)=1〉→|1〉,|5S1/2,F(xiàn)=2〉→|2〉,|5P1/2,F(xiàn)=2〉→|3〉和|5P3/2,F(xiàn)=2〉→|4〉。如圖1 所示,ωc和Ec分別是耦合|2〉與|3〉躍遷通道的正向強相干激光場的頻率和振幅;ωd和Ed分別是耦合|2〉與|4〉躍遷通道的反向強相干激光場的頻率和振幅;ωp和Ep分別是探測|1〉與|3〉躍遷通道的正向弱光脈沖的頻率和振幅。通過四波混頻過程,在|1〉與|4〉躍遷通道上會激發(fā)出一個頻率為ωs、振幅為Es的反向感生探測脈沖場。
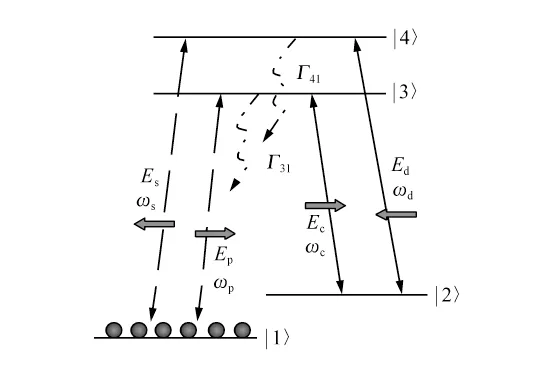
圖1 與兩個弱探測信號和兩個強耦合場相互作用的四能級雙Λ 型原子模型能級圖Fig.1 Energy level diagram of a four-level double-Λ atomic system interacting with two weak signal fields and two strong coupling fields
將此模型的相互作用哈密頓量帶入劉維爾方程,可以得到描述模型原子能級分布和相干性的密度矩陣方程組。在弱光近似與共振條件下,可以將密度矩陣方程組簡化為:
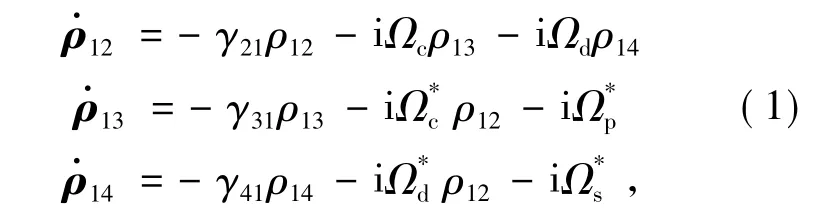
式中:Ωi(i=p,s,c,d) 為相應(yīng)激光場的Rabi 頻率,γa1(a=2,3,4) 為相應(yīng)能級間的相干弛豫速率。根據(jù)所選能級結(jié)構(gòu),γ21=0.2 kHz,在能級結(jié)構(gòu)Ⅰ中γ31= γ41=5.75 MHz,在能級結(jié)構(gòu)Ⅱ中γ31=5.75 MHz,γ41=6.07 MHz。
結(jié)合電磁場波動方程和極化強度關(guān)系P=Ndabρba,在慢變化近似條件下可得:
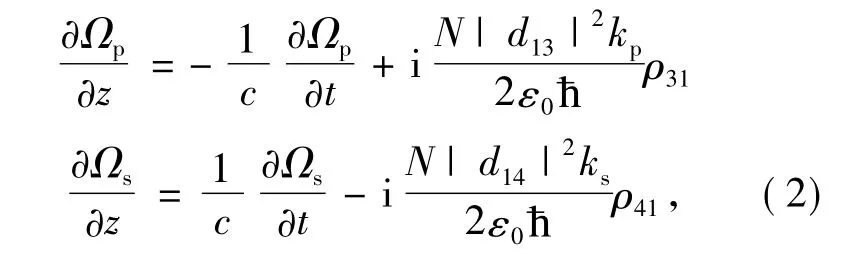
式中,d1a(a=3,4) 為相應(yīng)能級間的躍遷電偶極矩。
方程(1) 和(2) 組成了光信號的密度矩陣-麥克斯韋方程組,可以用來描述光信號在動態(tài)傳播過程中的光學(xué)特性。
3 結(jié)果分析
3.1 靜態(tài)光生成
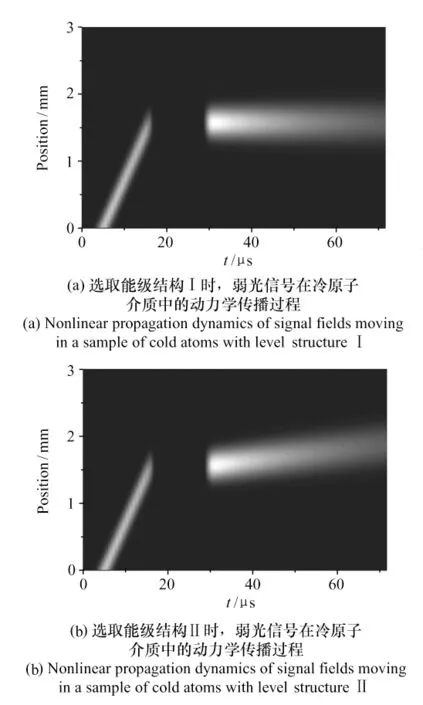
圖2 光信號存儲與靜態(tài)光信號制備過程Fig.2 Generation of optical signals for light storage and SLPs
圖2 ( a) 表示采用能級結(jié)構(gòu)I 時,光信號的動態(tài)傳播過程。激光場波長λp=λs=780.778 nm,λc= λd=780. 778 nm,偶極矩d13=d14=1. 0 ×10-29C·m,原子密度N=1.0 ×10-13cm-3。首先,在t= 0 時單獨開啟正向耦合激光Ωc=10 MHz直到t≈17 μs 時絕熱關(guān)閉。在此期間正向光脈沖信號會緩慢地進入介質(zhì)并轉(zhuǎn)化為自旋原子相干的空間波包,儲存在介質(zhì)中。當t≈29 μs時,同時開啟Rabi 頻率均為10 MHz 的正反兩個行波耦合激光,自旋原子相干的空間波包又絕熱轉(zhuǎn)化為正反向兩個光信號,但它們未向前移動,而是靜止耦合在介質(zhì)中,從而獲得靜態(tài)光信號。根據(jù)參考文獻[15]可知,傳統(tǒng)的利用駐波耦合介質(zhì)生成靜態(tài)光時,雙色駐波耦合激發(fā)了光學(xué)原子相干和自選原子相干的一系列高階空間傅里葉分量,使靜態(tài)光快速產(chǎn)生損耗和色散,即靜態(tài)光能量快速損失。相比之下,這里所選取的機制,靜態(tài)光能量損失就慢得多,能為許多光信號處理與量子比特控制提供充分的作用時間。
實驗時在能級結(jié)構(gòu)I 中,γ31=γ41,但是根據(jù)具體實驗或技術(shù)應(yīng)用的不同需求,會選擇不同的原子精細能級結(jié)構(gòu),這樣能級間弛豫速率會發(fā)生變化。圖2( b) 所示的光信號動態(tài)傳播,采用了能級結(jié)構(gòu)II 的87Rb 冷原子系綜,耦合場的時間調(diào)制則與前面完全相同。從圖2( b) 可見,由于γ31≠γ41,激發(fā)出的正反兩個光信號不平衡,故共同耦合出的光場非靜止而是發(fā)生緩慢的移動。
為了能夠重新獲取靜態(tài)光,作者通過比較Rabi 頻率的定義式Ω=dE/(2?) 與自發(fā)弛豫速率的關(guān)系式嘗試按比例:調(diào)節(jié)耦合激光場。
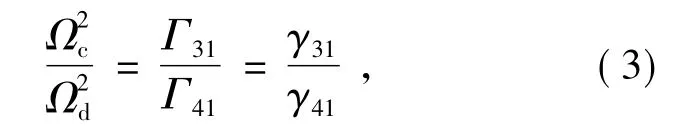
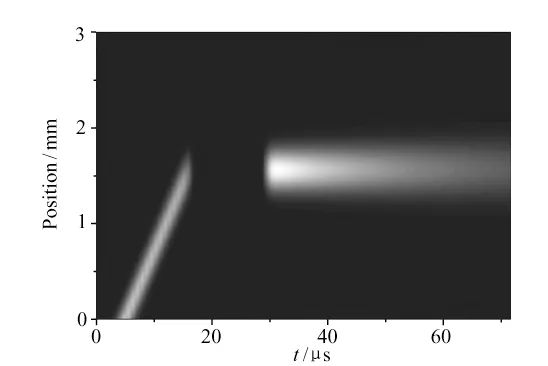
圖3 選取能級結(jié)構(gòu)Ⅱ時,弱光信號在超冷原子介質(zhì)中的動力學(xué)傳播過程Fig.3 Nonlinear propagation dynamics of signal fields moving in a sample of super cold atoms with level structure Ⅱ
圖3 表示采用能級結(jié)構(gòu)Ⅱ,在t≈29 μs 時同時絕熱開啟正反兩個耦合激光場制備靜態(tài)光,開啟Ωc=10 MHz,Ωd=10.27 MHz 條件下,光信號的動態(tài)傳播過程。如圖3 所示,通過按比例調(diào)節(jié)耦合激光場,在弛豫速率不相等時也能獲取令人滿意的靜態(tài)光信號,所以式( 3) 即為在形成靜態(tài)光信號時,調(diào)節(jié)耦合激光場所需滿足的必要條件。
3.2 相位調(diào)制
在此機制中,還可以對耦合激光場引入相位對靜止光信號進行調(diào)節(jié)。設(shè)φi(i=p,s,c,d) 為相應(yīng)激光場的相位。假如輸入的正向弱光信號的輸入相位為零,對兩個耦合場的相對相位( φd-φc)進行調(diào)節(jié)。圖4 表示當t≈31 μs 時,介質(zhì)中間位置的靜態(tài)光信號強度隨( φd-φc) 的變化。
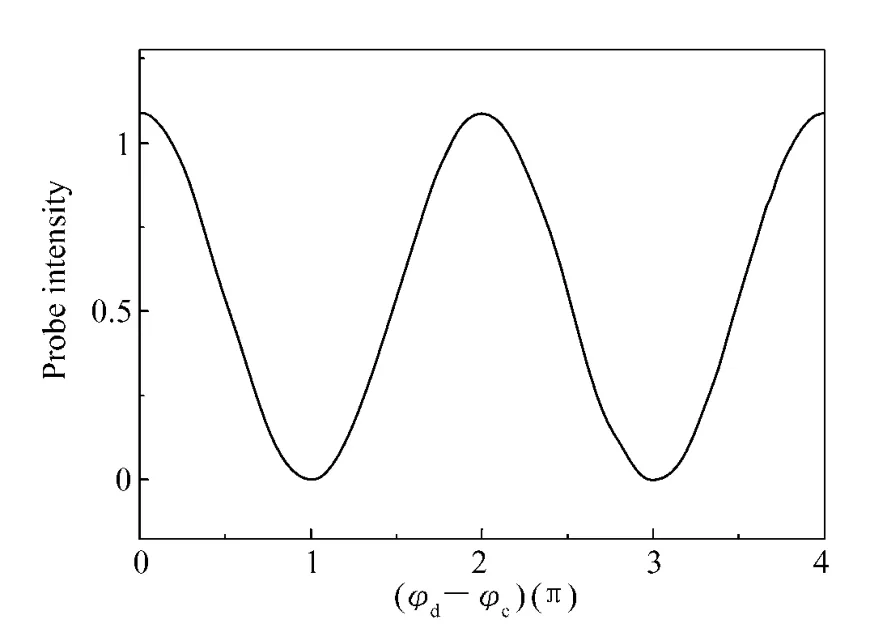
圖4 靜態(tài)光信號強度隨耦合場相對相位的變化Fig.4 Probe intensity as a function of relative phase of coupling fields
可見,隨著耦合場相對相位的變化,靜態(tài)光信號強度也隨之發(fā)生周期性的漲落。這是因為雙Λ型四能級經(jīng)4 個場耦合成一個閉合回路的形式[17-18]( 如圖1 所示) ,且反向弱光信號是經(jīng)過四波混頻過程激發(fā)出來的,滿足相位匹配條件,因此φp+φc-φd-φs=0,則φp-φs=φd-φc。所以,兩個弱光信號的相對相位( φp-φs) 會隨著( φd-φc) 發(fā)生變化,兩個弱光信號會發(fā)生周期性的相長或相消干涉,而它們疊加耦合成的靜態(tài)光信號強度就會周期性漲落。
4 結(jié) 論
本文根據(jù)獲取高效率、高保真度、長可持續(xù)時間存儲與靜態(tài)光信號的要求,建立了一個由正反雙向耦合場耦合冷87Rb 原子的四能級雙Λ 型能級的機制。利用這一機制,成功實現(xiàn)了一個易于全光調(diào)控、動態(tài)的系統(tǒng)過程,這個過程包含了光信號的導(dǎo)入、光信號的存儲、高保真度靜態(tài)光信號的生成,并可持續(xù)接近80 μs,能夠為光信號處理與量子比特控制提供充足的作用時間。研究了在生成靜態(tài)光時,調(diào)制耦合激光場所要滿足的條件,給出了利用相位對靜態(tài)光信號強度進行調(diào)制的方法。此機制為相關(guān)的光信息處理和量子計算技術(shù)提供了基本的、穩(wěn)定的操作環(huán)境支持,在制造量子計算器,全光元件、光子中繼器等器件時具有潛在的應(yīng)用價值。
[1] KIMBLE H J. The quantum internet[J].Nature,2008,453:1023-1030.
[2] HAMMERER K. Quantum interface between light and atomic ensembles[J].Rev. Mod. Phys.,2010,82:1041-1093.
[3] BAJCSY M,ZIBROV A S,LUKIN M D. Stationary pulses of light in an atomic medium[J].Nature,2003,426:638-641.
[4] CUI C L,JIA J K,WU J H,et al.. Ultraslow and superluminal light propagation in a four-level atomic system[J].Phys.Rev. A,2007,76:033815.
[5] PUGATCH R,SHUKER M,F(xiàn)IRSTENBERG O,et al.. Topological stability of stored optical vortices[J].Phys. Rev.Lett.,2007,98:203601.
[6] CHOI K S,DENG H,LAURAT J,et al.. Mapping photonic entanglement into and out of a quantum[J].Nature,2008,452:67-71.
[7] ANDRE A,LUKIN M D. Manipulating light pulses via dynamically controlled photonic band gap[J].Phys. Rev. Lett.,2002,89:143602.
[8] WU J H,LAROCCA G C,ARTONI M. Controlled light-pulse propagation in driven color centers in diamond[J].Phys.Rev. B,2008,77:113106.
[9] ZHANG Y,XUE Y,WANG G,et al.. Steady optical spectra and light propagation dynamics in cold atomic samples with homogeneous or inhomogeneous densities[J].Opt. Express,2011,19:2111-2119.
[10] ZHAO L,WANG T,YELIN S E. Two-dimensional all-optical spatial light modulation with speed in coherent media[J].Opt. Lett.,2009,34:1930-1932.
[11] de CARVALHO S A,de ARAUJO L E E. Electromagnetically-induced phase grating: A coupled-wave theory analysis[J].Opt. Express,2011,19:1936-1944.
[12] BAJCSY M,ZIBROV A S,LUKIN M D. Stationary pulses of light in an atomic medium[J].Nature,2003,426:638-641.
[13] WU J H,ARTONI M,LAROCCA G C. All-optical light confinement in dynamic cavities in cold atoms[J].Phys. Rev.Lett.,2009,103:133601.
[14] LIN Y W,LIAO W T,PETERS T,et al.. Stationary light pulses in cold atomic media and without bragg gratings[J].Phys. Rev. Lett.,2009,102:213601.
[15] WU J H,ARTONI,LAROCCA G C. Decay of stationary light pulses in ultracold atoms[J].Phys. Rev. A,2010,81:033822.
[16] WANG D W,LI Z H,ZHENG H,et al.. Time evolution,Lamb shift,and emission spectra of spontaneous emission of two identical atoms[J].Phys. Rev. A,2010,81:043819.
[17] WANG L G,QAMAR S,ZHU S Y,et al.. Manipulation of the Raman process via incoherent pump,tunable intensity,and phase control[J].Phys. Rev. A,2008,77:033833.
[18] HAO X Y,LI L H,Lü X Y,et al. Controllable amplification and absorption properties in coupled-double-quantum-wells with tunneling-induced interference[J].Eur. Phys. J. D,2010,56:239-246.

