論科學證據的兩種概率解釋

方輕

(廈門市委黨校哲學教研室，福建廈門361008)

用概率的理念與方法研究科學證據和確證問題在卡爾納普之后受到許多學者的重視。可以把下面這個句子看作關于證據的最本質的一種概率陳述，它為證據研究引進了概率概念:

(a)在已知e的情況下，h的概率為r，即p(h/e)=r。

概率的計算規則是概率觀念的核心部分。幾乎所有的概率論者都認為在使用概率概念或方法時必須服從一些基本的概率計算規則。這些規則包括:

①0≦p(h/e)≦1;

②如果h和h’邏輯等值，并且e和e’邏輯等值，那么 p(h/e)=p(h’/e’);

③p(～h/e)=1－p(h/e);

④ p(h∨h’/e)=p(h/e)+p(h’/e)－p(h∧h’/e);

⑤ p(h∧h’/e)=p(h/e) ×p(h’/h∧e).

規則①規定了概率值必須在0－1之間浮動;規則②要求邏輯等值的假說在邏輯等值的證據的支持下獲得同樣的概率;規則③規定一個假說的矛盾假說的概率等于1減去這個假說的概率;規則④和規則⑤分別是關于兩個假說的析取與合取的概率計算規則。這五條規則被認為是概率計算的基礎，所有從p(h/e)=r的形式發展而來的概率計算及其解釋都應該滿足以上這些計算規則。

一、科學證據的兩種概率定義

(一)“正相關”定義

證據的“正相關”定義是基于概率的證據定義或證據與假說概率之間關系的最常見的形式，幾乎所有在研究證據問題時涉及到概率分析的哲學家都會采用或贊同這一定義。所謂正相關，是指證據與假說的概率之間的正相關。這種以正相關為核心的證據定義可以表述為:

(b)e是h的證據當且僅當在已知e的情況下的h的概率大于未知e的情況下的h的概率，即p(h/e)＞p(h)。

具體而言，在證據與假說的概率之間，如果e改變了h的概率，那么e與h是相關的;如果e提高了h的概率，那么e與h之間的相關是正相關，e是確證h的證據;如果e降低了h的概率，那么e與h之間的相關是負相關，e是否證h的證據。由于通常人們在說“e是h的證據”時，都是指“e是確證h的證據”。因此，我們可以直接把第一種證據概率觀中的證據定義稱作證據的“正相關”定義。

我們可以把e與h之間的負相關轉變為e與～h之間的正相關，因此，把(b)中的h用～h代替，該定義同樣適用:

(b1)e是～h的證據當且僅當在已知e的情況下的～h的概率大于未知e的情況下的～h的概率，即p(～h/e)＞p(～h)。

由于證據和假說之間的關系通常都會受到理論背景或附加信息的影響，因此有些概率論的證據分析會把這一因素考慮進去，從而把證據的第一種概率定義作如下變化:

(b2)相對于特定的b，e是h的證據，當且僅當p(h/e∧b)＞p(h/b)。(b泛指理論背景)(b2)是(b)的延伸，它表明相對于特定的理論背景，如果e的存在提高了h的概率，那么e是h的證據。

同樣，我們可以把(b2)中的h用～h代替，得到:

(b3)相對于特定的b，e是～h的證據，當且僅當p(～h/e∧b)＞p(～h/b)。

由于p(～h/e∧b)＞p(～h/b)當且僅當p(h/e∧b)﹤p(h/b)，因此(b3)表明相對于特定的理論背景，e是～h(即否證h)的證據，當且僅當e的存在提高了～h的概率(即降低了h的概率)。

(二)“高概率”定義

除了“正相關”之外，還有第二種證據的概率定義，即所謂的證據的“高概率”定義。雖然由于在規定高概率的起點時會產生分歧，導致這種定義的普遍性不及“正相關”定義，但是它仍然具有相當的合理性，并且受到卡爾納普的青睞。

我們可以把證據的“高概率”定義表述如下:

(c)e是h的證據，當且僅當p(h/e)＞k。(k是高概率的起點)。

一般來說，作為高概率的起點是一個固定不變的數值。雖然卡爾納普提倡從“高概率”的角度定義證據，并且在他看來應該有一個固定的、單一的k的值存在，但是，他并沒有為高概率的起點規定一個明確的值。后來的一些哲學家，如阿欽斯坎，提議根據0≦p≦1的概率規則，把高概率的起點定為1/2，并且設定這個k值對于所有涉及證據評估的語境都適用。因此，第二種證據的“高概率”定義可以表述為:

(c1)e是h的證據，當且僅當p(h/e)＞1/2。一般的概率論認為一個假說非真即假(本文最后一部分將表明這種觀點是有問題的)即p(h)+p(～h)=1，也就是說，如果選擇k=1/2，那么p(h/e)＞1/2當且僅當p(～h/e)＜1/2。因此，第二種證據的“高概率”定義也可以表述為:

(c2)e是h的證據，當且僅當e使h的概率超過～h的概率，即p(h/e)＞p(～h/e)。

以上提及的兩種證據的概率定義體現出兩種不同的證據概率解釋，正如卡爾納普所說:第一種定義側重于證據效用的相對意義，即證據使假說“更穩固”或“更可接受”;第二種定義側重于證據效用的絕對意義，即證據使假說“穩固”或“可接受”。在實際研究中采用哪一種定義或概率觀更合適?這個問題對于不同的研究者有不同的回答。一般來說，主要對證據或確證問題進行定性研究的學者更多地采用“正相關”解釋，而熱衷于對證據或確證問題進行定量研究的學者則會在同時采納兩種觀點的基礎上對其中一種更加偏愛。

二、“正相關”與“高概率”的運用

(一)科學證據中的“比較級”

所謂科學證據中的“比較級”問題即具有以下形式的證據陳述:

(1)e對于h而言比對于h’而言是更強的證據。

(2)對于h而言，e比e’是更強的證據。

首先，以證據的“正相關”定義為基礎，即以“e是h的證據當且僅當e提高了h的概率”的概率觀為基礎，可以認為，如果e對于h而言比對于h’而言是更強的證據，那么e使h提高的概率必須超過e使h’提高的概率。形式化表述為:

(1’)e對于h而言比對于h’而言是更強的證據，當且僅當p(h/e)－p(h)＞p(h’/e)－p(h’)。同理，如果e比e’是h的更強的證據，那么e使h提高的概率必須超過e’使h提高的概率。形式化地表述為:

(2’)對于h而言，e比e’是更強的證據，當且僅當p(h/e)－p(h)＞p(h/e’)－p(h)。

其次，以證據的“高概率”定義為基礎，即以“e是h的證據當且僅當e使h的概率超過1/2(或其他較高的概率值)”的概率觀為基礎，可以認為，如果e對于h而言比對于h’而言是更強的證據，那么就要求e使h達到的概率超過e使h’達到的概率。這種解釋可以形式化表述為:

(1”)e對于h而言比對于h’而言是更強的證據，當且僅當p(h/e)＞p(h’/e)＞1/2。

同理，如果對于h而言，e比e’是更強的證據，那么就要求e使h達到的概率超過e’使h達到的概率。同樣，e或e’必須首先滿足各自是h的證據，即滿足p(h/e)＞1/2和p(h/e’)＞1/2，并可形式化表述如下:

(2”)對于h而言，e比e’是更強的證據當且僅當p(h/e)＞p(h/e’)＞1/2。

只需通過簡單的數學計算，上述兩種證據定義的概率觀對“比較(級)的”證據陳述的解釋實際上存在著(1’)=(1”)和(2’)=(2”)的關系。這說明，雖然兩種概率觀對證據的定義有所不同，但是將它們的思想用于解釋同一證據與不同假說或不同證據與同一假說之間的關系時，所得到的結果是一致的。兩種證據的概率解釋在本質上是不矛盾的。

(二)科學證據的“可接受性”

當“可接受性”作為一個描述某種特征或屬性的詞語被用于形容一個假說時，人們通常認為會有兩種結果出現:假說具有或不具有可接受性。這種定性的描述受到高概率論者的歡迎。因為，對假說進行“非是即否”的可接受性判斷，暗示了一個概率的分界點(即高概率的起點)的存在。“高概率”的支持者會這樣解釋:如果證據使假說具有高概率，或者說使假說的概率超過了某個高概率的起點，那么假說即具有了可接受性;反之，如果證據沒有使假說具有高概率，或者說沒有使假說的概率超過某個高概率的起點，那么假說不具有可接受性。

“正相關”理論的支持者不喜歡“可接受性”的說法，因為他們不愿意或認為不可能在假說所具有的概率中找出一個明確的分界點。這些概率論者更歡迎一種相對模糊的說法——“可接受性程度”。他們認為:如果證據使假說的概率比沒有該證據存在時更高，那么證據就使假說具有了更高的可接受性程度;如果證據無法使假說的概率比沒有該證據存在時更高，那么該證據就沒有使假說具有更高的可接受性程度。

其實兩種證據的概率觀解釋證據的“可接受性”也是不矛盾的。

首先，概率論對“可接受性”(或“可接受性程度”)的解釋通常可以從概率與可接受性(或可接受性程度)之間的關系上來把握。這一關系可以通過圖1直觀地表現出來。

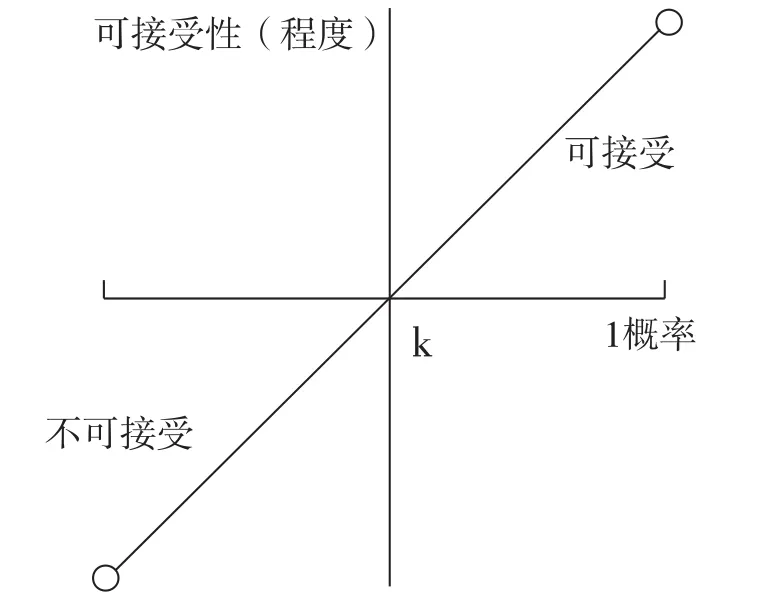
圖1 “可接受性”與概率的關系

在圖1中，橫軸表示概率，并且0≦p≦1;縱軸表示可接受性(程度);k表示可接受性要求達到的概率起點(即高概率起點)。從圖1中至少可以看出概率論對可接受性(程度)的以下幾個解釋要點:

(d)存在一個高概率的起點k。

雖然(d)看上去似乎是“高概率”一派所主張的，但是，即使“正相關”概率觀沒有明確提出需要一個高概率起點，甚至反對設立這樣一個高概率起點，但是實際上，這個作為界限的起點還是存在的或必需的。“正相關”的支持者可能會把可接受性理解為與假說的概率值從0到1變化正相關的假說可接受程度的變化，但事實上沒有任何一個“正相關”概率論者會贊同某個假說只要具有非0的概率或可接受程度，它就是可接受的;他們也不會認為一個信息只要能夠使假說的概率非0，它就是這個假說的證據。如果按照嚴格意義的“正相關”概率觀，科學就將成為“無門檻”或“低門檻”的:證據之為證據，只需使假說從極度荒謬上升為一般荒謬;假說之所以更穩固或更可接受，也只需找一個比自己更不穩固或更不可接受的假說作為陪襯。因此，高概率的起點是可接受性概率解釋的必要前提。

(e)假說h可接受當且僅當它的概率高于k。對于概率論者而言，高概率不僅是證據之為證據、假說“(更)穩固”或“(更)可接受”的必要條件，也是充分條件。(e)除了表明“當且僅當h的概率高于k時，h是可接受的”，還暗示了“當且僅當h的概率低于k時，h是不可接受的”。概率論者認為，為假說設立一個高概率的“門檻”能夠避免一些太弱的或不相干的證據對假說產生虛幻的、干擾性的影響。如果沒有k作為分界點，那么證據與假說的關系將只能通過“正相關”原則來解釋:e是h的證據當且僅當h依靠e(與b的合取)時比不依靠e(僅依靠b)時更可接受;也可以解釋為:e是h的證據當且僅當h依靠e(與b的合取)時比不依靠e(僅依靠b)時更非不可接受。這兩種“正相關”的概率解釋可以理解為把圖1中的曲線分割開來加以描述:前者描述了橫軸以上的屬于“可接受”部分的曲線，后者描述了橫軸以下屬于“不可接受”部分的曲線。這就為弱的或不相干的證據提供了存在的依據:e可以不用使h達到“可接受”，甚至不用使h變得“更可接受”，而只需簡單地使h“更非不可接受”。可以通過一個例子看出這種確認證據的原則會產生怎樣的結果。作為熱力學第二定律的一個著名宇宙學推論，“熱寂說”(h)預言了:“宇宙在遙遠的將來有一個不可避免的靜止和死亡狀態。”假設有兩種情況，情況e1:“宇宙現在處于一種活動和非死亡的狀態;”情況e2:“宇宙現在已經處于靜止和死亡狀態。”由于e2和h顯然是矛盾的，也就是說 p(h/e2)≡0，因此p(h/e1)＞p(h/e2)必然成立。根據“正相關”概率觀，這個恒成立的不等式表明e1比e2提供了更多的理由相信h。也就是說，由于e1比e2提供了更少的理由不相信h，因此，e1是h的證據;由于“宇宙現在處于一種活動和非死亡的狀態”是“宇宙在遙遠的將來有一個不可避免的靜止和死亡狀態”的證據，這顯然是很荒謬的。

(f)當假說h的概率等于k時，假說既非可接受，也非不可接受。

由于無論是傾向于“正相關”還是傾向于“高概率”的概率觀，很少有學者為k賦以一個明確的值(k=1/2的觀點只是少數情況下的權宜之計)，因此，在概率論者那里，幾乎不存在p(h/e)=k的情況，因此，對于“當p(h/e)=k時h的可接受性如何”的概率解釋是懸而未決的。

(g)假說的可接受性原則上不會達到絕對可接受或絕對不可接受。

即使有少數概率論者認為存在證實性證據或毀滅性證據，它們可以使假說的概率達到極限值，即p(h/e)=0或p(h/e)=1，但是，更普遍的觀點是:由于假說的概率難以達到極限值，因此假說在可接受性上難以達到相應的極限，即絕對可接受或絕對不可接受。

其次，“可接受性”(或“可接受性程度”)的概率解釋還可以從根據假說的概率對假說的可接受性進行的等級劃分上來理解(如圖2)。

圖2 “可接受性”的分級表示

圖2中的橫軸表示概率，并且0≦p≦1;縱軸表示可接受性等級;k表示高概率起點。在圖2中，可以看出以下幾點:

(h)假說的概率在0－1之間被劃分為不同的等級(區間)。

有些概率論者會把假說的可接受性劃分為不同的等級，劃分等級的依據就是假說的概率的高低。因此，這里實際上存在兩次等級的劃分:第一次是為假說的概率劃分等級，形成連續的等級區間，第二次是依據假說概率的等級為假說的可接受性劃分等級。例如，圖2 中以0、k’、k、k”、1 為界限把假說按概率高低分為四個連續的區間:(0，k’)、(k’，k)、(k，k”)、(k”，1)。k’、k”的作用與 k 基本相同——都是作為概率級別的某個分界點，但由于重要性上的不同——k可為假說定性，k’、k”只能對假說進行程度說明，因此，如果我們可以認為k是一級的高概率起點，那么k’、k”則是二級的高概率起點。與k的賦值情況相同，概率論者幾乎都回避了給k’、k”這樣的二級高概率起點一個明確的值，為了便宜行事，有時會效仿k的賦值為k’、k”取一些折中的數值，如1/4、3/4等。

(i)根據假說h的概率所屬的不同區間，假說的可接受性被劃分為不同的等級。

表示假說概率的橫軸被劃分出幾個連續的區間之后，就可以在縱軸上相應的位置劃分出幾個不同的可接受性等級。如圖2所示，可接受性等級包括可接受的等級和不可接受的等級。我們可以說:概率在(k，k”)區間內的假說，屬于較低的可接受等級(或級別1);概率在(k”，1)區間內的假說，屬于較高的可接受等級(或級別2);概率在(k’，k)區間內的假說，屬于較低的不可接受等級(或級別－1);概率在(0，k’)區間內的假說，屬于較高的不可接受等級(或級別－2)。

(j)沒有規定假說h的概率等于分界點值時，即p(h)=0或k’或k或k”或1時，假說的可接受等級情況。

(j)實際上是(c)與(d)的綜合，原因也大致相同:一方面，k、k’、k”的值并不確定，另一方面，極限狀態幾乎不可能達到。

圖2是一個梯級函數曲線示意圖。雖然假說的概率覆蓋了從0到1所有可能出現的概率值，但是可接受性等級卻只有4個(級別1、級別2、級別－1和級別－2)，即使加上概率論沒有做出解釋的幾個分界點和極限值的可接受性等級歸屬，可接受性級別的個數還是有限的。這就可能造成這樣的結果:兩個不同的假說，雖然擁有不同的概率，但被歸入同一個可接受級別。這種情況就如同兩個學生的考試成績分別為86分和99分，如果根據“85分以上為優秀”的等級劃分，則這兩個差距明顯的成績仍然被歸入同一級別。為了實現對可接受性的等級劃分，以犧牲較小概率差別為代價，是概率解釋難以兩全的必然選擇。因此，只有綜合圖1和圖2所包含的所有概率解釋要點，才能夠比較全面地把握對假說可接受性的概率解釋。不難發現，實際上圖1和圖2是相通的:只需將圖2中的級別數量無限增加，就可以使圖示從圖2中的那個梯級函數曲線變成圖1中的那條平滑連續的函數曲線(如圖3所示)。

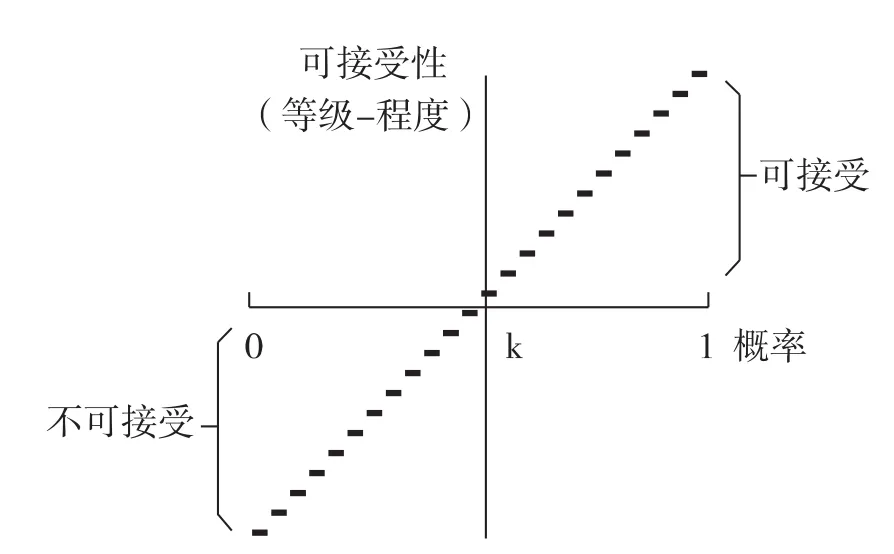
圖3 “可接受性”等級無限增加的過程

三、“正相關”與“高概率”的局限性

“正相關”與“高概率”不僅給科學證據做出了兩種直觀明確的定義，并且能夠清晰簡潔地揭示科學證據研究中的許多具體問題。然而，“正相關”和“高概率”對科學證據的定義本身卻存在著不可彌補的缺陷。

(一)“正相關”不是證據的充要條件

即使在概率解釋上正相關概率論者不得不默認有必要在證據與假說的關系中設立一個特定的高概率起點，但是，他們的核心觀點仍然是:證據之為證據，必須能夠使假說的概率在出現證據之后有所提高，即證據必須與假說的概率正相關。對于正相關概率觀，人們很容易就會提出這樣的疑問:是否提高了假說的概率，就可以成為假說的證據?此外，是否要成為假說的證據，必須提高假說的概率?

設想這樣一種情況:湯姆生在1897年前后做了1 000次“陰極射線通過磁場”的實驗，其中999次的實驗結果是“陰極射線通過磁場時不發生偏轉”，1次的實驗結果是“發生偏轉”。后來，湯姆生發現，在之前的999次實驗中，有900次存在諸如“玻璃瓶中真空指標嚴重不達標”等技術失誤，因此，他否定了這900次實驗結果的有效性。因此，現在的情況是:100次有效的實驗結果中，99次“陰極射線通過磁場時不發生偏轉”，1次“發生偏轉”。如果(根據邏輯等值原則)直接以“陰極射線通過磁場時發生偏轉”的實驗結果預期代替“陰極射線帶電”作為湯姆生的假說，則有如下關系:

b:在第一時間段里，湯姆生一共做了1 000次“陰極射線通過磁場”的實驗，其中999次“陰極射線不發生偏轉”，1次“發生偏轉”。

e:在第二時間段里，湯姆生否定了999次“不發生偏轉”的實驗結果中的900次實驗結果的有效性，剩余的99次“不發生偏轉”和1次“發生偏轉”的實驗結果繼續維持有效性。

h1:陰極射線通過磁場時發生偏轉。

h2:陰極射線通過磁場時不發生偏轉。

在這個例子中，假說的概率分配、以及在證據基礎上的概率變化是這樣的:

p(h1/b)=1/1000

p(h2/b)=999/1000

p(h1/b∧e)=1/100

p(h2/b∧e)=99/100

從概率上看，e的出現使h1的概率從1/1000變為1/100，整整提高了10倍。根據“正相關”概率觀，由于p(h/b∧e)＞p(h/e)，所以，e完全有資格成為h1的證據。但是，我們是否就可以因此認為e是h1的證據呢?在面對1/1000或1/100這樣實在不可謂高的概率值時，如果沒有對“真理往往掌握在少數人手里”的堅強信念，恐怕很少人會選擇肯定的答案。因此，e提高了h1的概率并不是e是h1的證據的充分條件。

如果從e與h2的關系上看，我們甚至發現，e提高了h2的概率不是e是h2的證據的必要條件。與h1相比，e的出現對h2的影響相對小一些，它使h2的概率從999/1000變為99/100，也就是說p(h2/e∧b)﹤p(h2/b)。如果根據“正相關”原則，e降低了h2的概率，那么e不僅不是h2的(確證)證據，而且應該成為h2為假的證據，即反對h2的證據，或者在該例中直接成為支持h1的證據。但是，實際的情況是，e即使使h2的概率有所減小，可從絕對值上看，h2的概率(無論是999/1000還是99/100)始終對h1的概率有著壓倒性的絕對優勢。以p(h2/b∧e)和p(h1/b∧e)之間的懸殊來看，真理的天平依然是傾斜向h2一方的，e仍然被大多數人看作是支持h2的。于是，e提高h2的概率不再是e是h2的證據的必要條件。

上面這個例子表明:有可能存在某個事實或陳述提高了假說的概率，但卻沒有成為假說的證據，而某個事實或陳述減小了假說的概率，但它卻仍然被認為是這個假說的證據。

(二)“高概率”不足以使證據之為證據

那么，“高概率”是否是證據之為證據的必要條件或充分條件呢?本文認為，“高概率”是一個事件或信息成為假說的證據的必要條件，但不是充分條件。如果沒有高概率的起點設置，那么煉金術士的信念將因其比柏拉圖的哲學理念更像科學而堂而皇之地成為科學;如果沒有高概率的起點設置，那么宇宙現在沒有熱寂將僅僅因為它沒有與將來的熱寂發生矛盾而成為熱寂說的證據。因此，證據是假說達到高概率是證據之為證據的必要條件。那么，問題就被集中到了:高概率是證據之為證據的充分條件嗎?

眾所周知，1919年5月29日，愛丁頓拍攝到了日全食時由于太陽重力使光線彎曲而導致太陽附近行星的位置發生了改變。這一觀測事實被作為愛因斯坦相對論的重要證據載入史冊。假設:

e1:1919年5月29日發生日全食。

e2:1919年5月29日，愛丁頓觀測隊在發生日全食時拍攝到了太陽附近的星光發生了1.7秒的偏轉。

h:引力場會使光線發生偏轉。

在這個例子中，我們把那種普遍被科學家接受的觀點當作已知的，即e2使h達到了高概率，或p(h/e2)＞1/2。根據“高概率”概率觀，e2是h的證據。這是沒有問題的。在前一個式子的基礎上，我們可以得到p(h/e1∧e2)＞1/2。根據“高概率”觀點，我們將會得到“e1∧e2，即e1和e2的合取是h的證據”。這就有問題了。因此，即使p(h/e1∧e2)＞1/2，也不可以說“e1是h的證據”或“e1和e2的合取是h的證據。因為e1雖然是一個事實，并且看上去和e2的發生有著直接的關系，但是e1不僅與h沒有直接的因果關系，也與e2中對h起確證作用的實質成分“太陽附近的星光發生了1.7秒的偏轉”沒有因果關系。因此，e1只是一個與h不相干的事實，即使p(h/e1∧e2)＞1/2，也不能夠說e1是h的證據，或e1∧e2是h的證據。也就是說，只有在p(h/e1∧e2)＞1/2并且e1和e2都各自對確證h做出了貢獻時，才可以說e1或e2、或e1和e2的合取是h的證據。通過這個例子，本文想表明的是:即使p(h/e1∧e2)＞1/2時，“e1∧e2是h的證據”也可能不是成立的，因此，“高概率”不是證據之為證據的充分條件。

［1］Peter Achinstein.The book of evidence［M］.New York:Oxford University Press，2001.

［2］PAUL K.Moser.Knowledge and Evidence［M］.New York:Cambridge University Press，1989.

［3］R.Carnap.Logical Foundations of Probability［M］.Chicago University press，1950.

［4］GLYMOUR C.Theory and Evidence［M］.Princeton university Press，1980:64.