黏彈性邊界條件在ANSYS有限元波場模擬中的實現*
王朝令 劉爭平
(西南交通大學,成都 610031)
黏彈性邊界條件在ANSYS有限元波場模擬中的實現*
王朝令 劉爭平
(西南交通大學,成都 610031)
在ANSYS軟件中應用黏彈性邊界單元,用Combin14單元完成了黏彈性邊界的施加。算例表明其可以很好地吸收邊界反射波,且當切向剛度參數不變,法向剛度參數變化時,吸收效果不受影響,反之亦然,驗證了其有效性和穩定性。
黏彈性邊界;彈性波場;有限元;ANSYS;地震波
1 引言
在波場數值模擬中,必須選用合理的有邊界限制的有限空間域,以使實際模擬是可行的,并保證計算量在計算機可承受的范圍內。但引入假定的邊界會導致虛假的邊界反射波。
采用有限元模擬時,通常采用時間域的透射邊界處理虛假的邊界反射波,這種邊界由一維或二維的條件導出,并使得沒有能量從邊界反射;其中應用最廣泛的是 Lysmer和 Kuhlmeyer引入的黏性邊界[1],它采用黏性阻尼代替遠場邊界;Novak提出了平面應變邊界[2],這種邊界主要應用于嵌入基礎和樁基;Deek在柱面波理論基礎上建立了二維時域人工邊界[3],但是平面應變邊界包含依賴于頻率的項,這對于在加載瞬態載荷的瞬態響應分析中會變的比較復雜。相比之下黏彈性邊界應用更廣泛,本文研究黏彈性邊界在商用有限元軟件ANSYS的地震波場模擬中的實現及其應用效果。
2 彈性波場中的黏彈性邊界條件
黏彈性人工邊界模擬的是人工邊界上的應力條件,因此是一種連續分布的邊界。根據劉晶波等[4]的研究結果,歸納的二維人工邊界等效物理系統的彈簧系數k和阻尼系數c在針對不同的邊界時分別為:
切向邊界
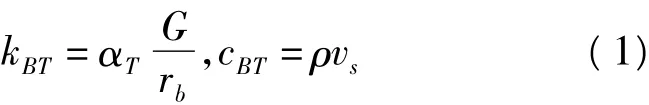
法向邊界
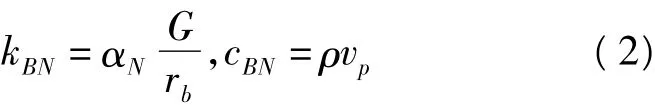
式中kBN、kBT分別是彈簧的法向與切向剛度,cBN、cBT分別是彈簧的法向與切向阻尼系數,rb為波源至人工邊界點的距離,vs和vp分別為S波和P波波速,G為介質剪切模量,ρ為介質質量密度,αT和αN分別為切向與法向黏彈性人工邊界參數,人工邊界比較合適的參數αT取值范圍為[0.35,0.65],αN的取值范圍為[0.8,1.2]。
3 黏彈性邊界條件在ANSYS中的實現
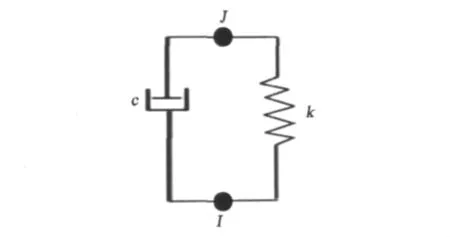
圖1 Combin14單元示意圖Fig.1 Sketch of Combin14 element
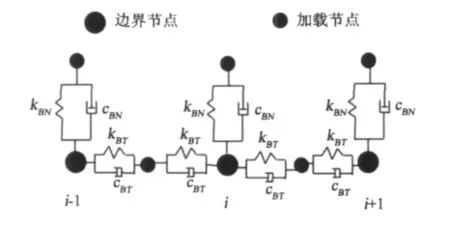
圖2 加載方式Fig.2 Loading mode
在ANSYS軟件中,適合用來做黏彈性邊界的單元選用Combin14,它在一維、二維或三維應用中具有軸向或扭轉性能,縱向阻尼彈簧為單軸壓縮張力單元,在每個節點有3個自由度:x、y和z軸,不考慮扭轉和彎曲。另外彈簧阻尼單元沒有質量矩陣,圖1為Combin14單元的示意圖,I、J為節點,k為剛度系數,c為阻尼系數。圖2是彈簧在ANSYS數值模擬計算中的加載方式,i-1、i、i+1為邊界的3個節點,切向加載是在兩個節點之間生成一個新的節點,在新的節點與邊界節點之間加載彈簧,切向剛度系數和阻尼系數由式(1)得到,法向加載是在邊界節點外側產生新的節點,加載方式與切向加載相同,法向剛度系數和阻尼系數由式(2)得到。
為驗證黏彈性邊界在通用有限元軟件ANSYS中的加載效果,構建如圖3所示的2D模型示意圖,尺寸為200 m×150 m,網格尺寸劃分為0.5 m,觀測系統為中間激發,兩邊接收,道間距為2 m,道數是48道,震源為100 Hz的Ricker子波,加載方向豎直向下,得到如圖4的時間記錄,左邊為直接將位移歸零的Dirichlet邊界在同樣的模型中所得到時間記錄,右邊為施加黏彈性邊界后的時間記錄。
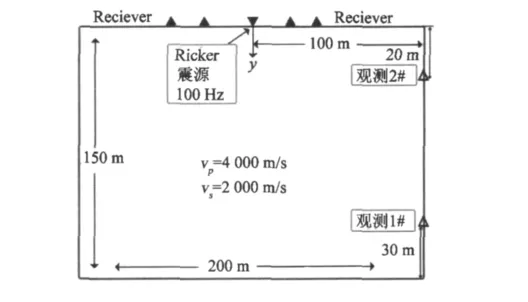
圖3 模型Fig.3 Model
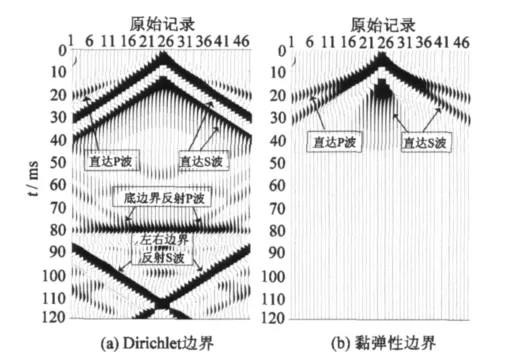
圖4 時間記錄Fig.4 Records of time
在模型四周施加黏彈性邊界后,圖4(b)中的P、S波都受到了抑制,且相較之下,S波受影響更大。除了直達P、S波之外,沒有別的邊界反射到接收排列上,證明了黏彈性邊界可以有效地吸收反射波,圖4(a)是在默認位移為零的Dirichlet邊界所得到的記錄,各邊界均有反射波返回到接收排列,使得對波的辨識和同相軸的判別都變得比較困難。圖5為Dirichlet邊界模型和加載黏彈性邊界模型的波場快照,對比相同時刻的快照可以看出,Dirichlet邊界的波場快照中各種反射波夾雜在一起,使得波場變得非常復雜,不易辨識,增加了資料處理的難度。
4 邊界條件的穩定性分析
為驗證加載黏彈性邊界和Dirichlet邊界的精確性,在模型圖3中標識出了觀測點1#、2#點的時間-位移記錄。圖6為黏彈性邊界點與Dirichlet邊界點的時間-位移曲線,其中實線表示施加了黏彈性邊界的1#、2#取樣點的時間-位移曲線,它的振幅很小;虛線表示默認初始位移為零的Dirichlet邊界的取樣點曲線的時間-位移曲線,它的震蕩很劇烈。
為驗證參數取值范圍的有效性,設置不同參數并進行模擬計算,提取觀測點1#、2#的時間-位移曲線。圖7(a)表示在施加的黏彈性邊界彈簧在切向剛度參數(αT)保持為0.5時,法向剛度參數(αN)分別為0.8、1、1.2時的時間-位移曲線。從圖中可以看到,在取不同法向剛度參數時,1#、2#取樣點的時間-位移曲線保持一致。圖7(b)是取樣點1#、2#的在法向剛度參數保持為1,切向剛度參數分別為0.35、0.5、0.65時的時間-位移變化曲線,1#、2#觀測點的時間-位移曲線也基本一致,從中可以得出黏彈性邊界具有很好的魯棒性。
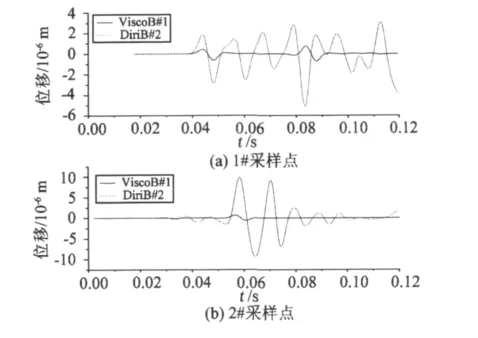
圖6 采樣點的位移比較Fig.6 Comparison of displacement at sampling point
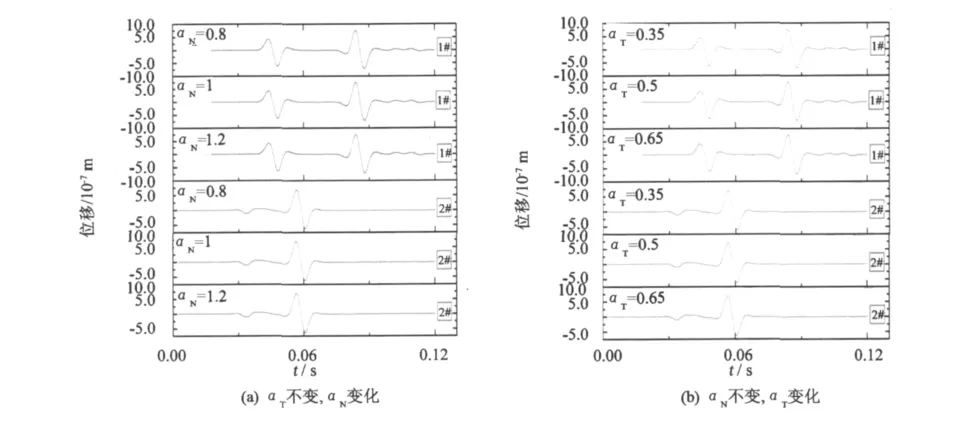
圖7 參數的對比Fig.7 Comparison of parameters
5 結論
本文引入黏彈性邊界的剛度系數和阻尼系數,將其應用到ANSYS軟件中,用Combin14單元完成了黏彈性邊界的施加,算例表明采用這種方法可以很好地吸收邊界反射波,且當切向剛度參數(αT)不變,法向剛度參數(αN)變化時,對邊界的吸收影響很小,反之亦然,證明了其具有良好的魯棒性。究其原因,黏彈性人工邊界單元本質上是一種真正的有限元[5],它的收斂性和精度等變化規律與普通有限單元相同,因此只要滿足有限元的基本要求,則加載邊界時的模擬計算結果就不會受太大影響。
1 Lysmer and Kuhlemeyer.Finite dynamic model for infinite media[J].Journal of Engineering Mechanics-Asce,1969,95 (4):91-100.
2 Novak and Hindy.Seismic analysis of underground tubular structures[A].Proceedings of the 7th World Conference on Earthquake Engineering[C].Istanbul Turk:Turk Natl Comm on Earthquake Eng.,1980.
3 Deeks,Randolph.Axisymmetrical time-domain transmitting boundaries[J].Journal of Engineering Mechanics-Asce,1994,120(1):25-42.
4 劉晶波,谷音,杜義欣.一致粘彈性人工邊界及粘彈性邊界單元[J].巖土工程學報,2006,28(09):1 070-1 076.(Liu Jingbo,Gu Yin and Du Yixin.Consistent viscous-spring artificial boundaries and viscous-springboundary elements[J].Chinese Journal of Geotechnical Engineering,2006,28 (09):1 070-1 076)
5 劉晶波,等.波動問題中的三維時域粘彈性人工邊界[J].工程力學,2005,22(06):46-51.(Liu Jingbo,et al.Three dimensional viscoelastic artificial aoundaries in time domain for wave motion problems[J].Engineering Mechanics,2005,22(06):46-51)
REALIZATION OF VISCOELASTIC BOUNDARY CONDITION IN WAVE FIELD SIMULATION WITH ANSYS FINITE ELEMENT SOFTWARE
Wang Chaoling and Liu Zhengping
(The Southwest Comunication University,Chengdu 610031)
We present a method to realize viscoelastic boundary condition in ANSYS finite element software by using the Combin 14 element.The numerical results show that the method can well absorb the boundary reflection wave,and is insensitive to change of boundary normal stiffness parameters while the tangential stiffness parameters keep constant,and vice versa.The results also verify the effectiveness and stability of the method.
viscoelastic boundary;elastic wave field;FEM;ANSYS;seismic wave
1671-5942(2012)02-0028-04
2011-11-09
國家自然科學基金(40874051)
王朝令,1980年生,博士研究生,主要研究方向為地震波場數值模擬研究.E-mail:wong8010@gmail.com
P315.8
A

