基于正交最小二乘多面函數構建局域海洋地磁場模型研究*

常宜峰 柴洪洲 王 敏

(解放軍信息工程大學測繪學院，鄭州 450052)

基于正交最小二乘多面函數構建局域海洋地磁場模型研究*

常宜峰 柴洪洲 王 敏

(解放軍信息工程大學測繪學院，鄭州 450052)

針對多面函數擬合局域海洋地磁場模型中質量控制和節點選擇問題，提出使用抗差估計與正交最小二乘原理相結合的方法。在質量控制過程中，將局部有顯著起伏的采樣點視為異常觀測值，采用抗差估計減弱異常值點的不利影響。在節點選擇中，使用基于正交最小二乘原則判斷節點的貢獻效力大小，按照此原則自適應地選擇節點。結果表明，基于正交最小二乘原理的多面函數法的精度和穩定性更好，更適于構建局域海洋地磁場模型。

局域海洋地磁場模型;抗差估計;正交最小二乘原理;多面函數;節點

1 引言

地磁場在了解地球內部的物質分布和輔助導航中有重要用途，其中，地磁場模型起著非常重要的作用。常用的是泰勒多項式模型，優點是計算簡單，但地磁數據存在較大跳變性，難以取得較高的精度。1971年Hardy給出了多面函數擬合法，1976年用于重力異常和大地水準面差距計算，1978年用于地殼形變計算，2009年趙建虎將此方法引入局域海洋地磁場建模中，并提出分區建模來提高精度［1］。多面函數是利用一些規則的數學曲面來逼近實際曲面，從而獲得較高的精度。本文提出將抗差估計與正交最小二乘相結合來擬合局域海洋地磁場模型。

對于多面函數模型，核函數的選擇和節點的確定至關重要。對于核函數，已有學者進行過深入研究。正雙曲面函數構建的模型在檢查點上的誤差分布和精度統計參數均優于倒雙曲面函數，并且正雙曲面核函數構造的模型精度隨平滑因子的變化平緩而相對穩定，倒雙曲面函數構造的模型精度變化劇烈且最優平滑因子相對較大，而過大的平滑因子可能造成局部模型失真，尤其對于地磁變化相對較大的數據的擬合，在此取正雙曲面函數，平滑因子取0.1［1］。對于節點的選擇，通常是直接取采樣點，可是選擇節點不同產生的結果也不同，具有一定的隨意性。由于每個節點對擬合結果貢獻是不同的，有學者采用t檢驗或逐步回歸的方法來選擇節點，得到的效果較好［2］。本文利用正交最小二乘原理的基本思想，首先將誤差方程系數正交化，并計算觀測向量與正交化向量之間的夾角，節點對曲面擬合的貢獻就用夾角的大小來表示。按照這種原則方法依次選擇合適的節點，完成自主選擇節點的目的［3］。此方法的優點是既保證了擬合的精度又兼顧了擬合的穩定性。

2 基于抗差估計的質量控制

在測量過程中受到各種因素的影響，可能出現異常觀測數據，一般的質量控制是采用判斷測量值與對應趨勢面擬合值之間差值大小的趨勢面法來進行的。趨勢面分析方法是將短尺度的、局部的變化看作隨機的和非結構的噪聲，因此當局部區域變化比較劇烈時，可將其視作異常觀測。但是單純的趨勢面擬合并不具備抗差的能力，故本文引入抗差估計理論［4，5］，采用抗差趨勢面法進行質量控制。

趨勢面函數如下式所示

其中，αij(i=0，…，n，j=0，…，n)為待求系數，(x，y)為觀測點坐標為對應的磁力觀測值。如果有m個觀測點，應用最小二乘準則即可解得多項式系數。

設有誤差方程

根據抗差估計理論，以及等價權理論可得

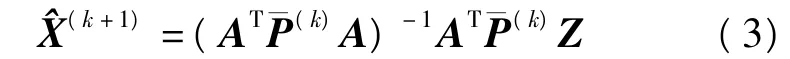
3 基于正交最小二乘法節點選擇

經過質量控制后，再對剩下的殘差進行擬合。根據多面函數原理有，

在已知有限測量數據的情況下求解方程，重要的是節點的選擇，一般情況下直接取均勻分布在研究區域內的觀測點，如果選擇所有的采樣點作為節點，可能會出現內符合精度虛高，推估和內插精度無法保證的情況。特別在采樣點受異常誤差污染時，擬合精度會更低。為解決以上問題，本文在此引入基于正交最小二乘原理的思想來建立一種自主選擇節點的方法。

在m個磁力數據中選擇n個數據建模，即

其中，X為模型系數，A為核函數矩陣，由最小二乘原理得，

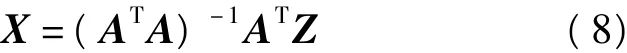
模型精度評價指標為［6］

其中，n為節點個數，(xi，yi)為節點坐標，βi為模型系數，Q(x，y，xi，yi)為二次核函數，一般取正雙曲函數(如下式)，δ2為模型的平滑因子(本文取0.1)。

先假設選取所有的采樣點為節點，即m=n，此時構建的誤差方程系數陣為

其中，

從式(11)可以看出，每個ai對求系數β的決定效力是有差別的，即每一節點對函數擬合的影響是不同的，故提供了一種評價準則，便于依照節點貢獻效力的大小來選擇節點。

下面就引入一種表示節點貢獻大小的原則，將式(5)表示成向量形式，

假設ak之間是相互正交的，則左乘βk有，

兩邊求和并移項得

定義η為選擇t(t≤m)個節點的列向量時的總貢獻

η的值在0到1之間。并且當t越大，η就越大，表明逼近程度越高;當t=m時，η=1，此時選擇了所有的采樣點，擬合誤差為零，逼近精度最高。但由于沒有多余觀測，可靠性較差，為此應根據每個基矢量的貢獻大小來選擇若干節點，使η足夠大且有多余觀測。

要想使η最大，即需使βk取最大值，在式(12)兩邊同時左乘，可得

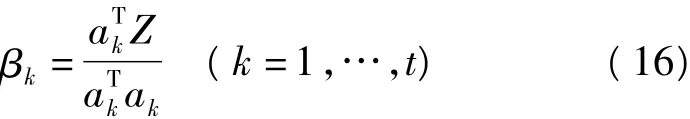
顯然，要使βk取得最大值，需向量ak與觀測向量Z之間的夾角θakZ最大，即

其具體計算步驟為:

1)將所有的采樣點視為剩余節點，計算系數陣A，m個列向量可記為a1，a2，…，am;

2)計算Z與ak之間的夾角，求得最大值

式(18)表明aj對Z的貢獻最大，于是可將與aj相對應的坐標(xj，yj)選為節點。

3)按照最小二乘原理解算系數β

4 實驗分析

為驗證以上所述方法在局域海洋地磁場模型建立中的有效性，采用某測區海洋磁力測量的數據進行計算和分析。該測區定位系統采用NGD-60型差分GPS定位系統，船載磁力儀采用美國Geometrics公司的G-881型海洋磁力儀，共有1 681個測量數據。經過了各項的改正，測區的等值線如圖1所示。均勻選取其中的441個數據作為已知的測量點，將剩余的測量數據作為外部的檢核點，分別使用多面函數法、正交最小二乘多面函數法、基于抗差趨勢面的多面函數法和基于抗差趨勢面的正交最小二乘多面函數法，4種方法進行計算(表1，其中最大值和最小值是指模型計算結果與實測值的偏離的最大和最小值，平均值是所有偏離量的算數平均值，均方誤差是對外部檢核點的綜合評價指標)。

圖1 某測區磁力異常分布Fig.1 Distribution of magnetic abnormity in the studied area

表1 不同擬合方法的結果比較(單位：nT)Tab.1 Comparison among results with different methods (unit：nT)

從表1可以看出，直接使用多面函數和正交多面函數進行擬合，均方誤差分別可達17nT和15nT，平均值都在0.6 nT左右，說明模型的集中程度較好，兩者所得到的精度基本相當，但正交多面函數法略好于多面函數法，并且都有所偏大。加上抗差估計趨勢面進行質量控制之后，同樣比較兩種方法的計算結果，均方誤差分別為12 nT和7 nT，精度提高了41%，平均值分別為-8.4 nT和0.2 nT，基于抗差趨勢面的多面函數出現了明顯的系統偏差，分析原因是多面函數法對節點沒有選擇性，不是選擇一些特征節點進行建模，而是將所有的節點作為建模節點，從而引入了一些系統誤差，進而產生了系統性偏差。比較多面函數和基于抗差趨勢面的多面函數，增加了抗差以后，精度由17 nT變為12 nT;同樣，對正交多面函數增加了抗差以后，精度由15 nT變為7 nT，說明基于抗差趨勢面的質量控制可以減小一部分不良影響。綜合表明基于抗差趨勢面的正交多面函數法總體上要優于以上其他3種方法。

圖2和圖3分別是使用基于抗差趨勢面的正交多面函數法和基于抗差趨勢面的多面函數法擬合的檢驗點的殘差分布圖，從圖中可以看出，圖2的殘差分布相對更為集中，且普遍都靠近零點。

為進一步驗證按照正交多面函數法選擇節點的多少與所得模型擬合精度之間的關系，依次計算了選擇個檢驗點時的均方誤差，并將用正交多面函數選擇的節點個數與擬合的均方誤差的關系繪制成圖4。

圖2 基于抗差趨勢面的正交多面函數法擬合殘差Fig.2 Fitting residual with orthogonal multi-function method based on robust trend-surface

從圖4可以看出，隨著選擇的節點個數的增加，均方誤差逐漸減少。在采用250個節點時，精度已經達到了17 nT，基本上相當于選擇所有節點進行多面函數法建模時的精度。隨著選擇節點個數的繼續增加，精度基本保持穩定并有所提高。同時應該指出，針對地磁變化比較復雜和比較平緩的兩種區域，數據的代表性對于模型的精度有著重要的影響。因此，在變化比較復雜的區域可以適當的放寬迭代停止的判斷條件，盡可能多的自主選擇特征點進行建模。

圖3 基于抗差趨勢面的多面函數法擬合殘差Fig.3 Fitting residual with multi-function method based on robust trend-surface

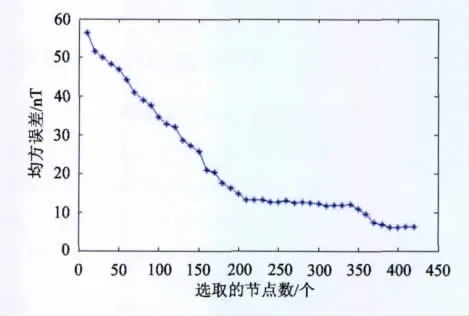
圖4 節點選擇與擬合誤差關系Fig.4 Relation between node collecting and error fitting

圖5 兩種方法擬合效果比較Fig.5 Comparion between fitting results with two methods

為了使計算結果更直觀，用正交多面函數法和一般多面函數法分別計算了整個區域的網格點地磁場總強度值，并利用計算所得數據分別繪制正交多面函數法和普通多面函數法磁力異常圖，與該區域實際磁力異常場圖進行比較。圖5(a)是原始的磁力異常分布圖，(b)是使用基于抗差趨勢面的正交多面函數法得到的擬合圖，(c)是使用基于抗差趨勢面的多面函數法得到的結果。從圖中可以看出，圖5(b)與(a)等高線的分布較為接近，顯現出了較為細節的分布信息，保持了較高的一致性;(c)與(a)的一致性較差。從而顯示圖5(b)的建模方法是穩定可靠的。

5 結論

1)進一步驗證了多面函數法比較適用于局域海洋地磁場建模，在地磁變化復雜的海域，先進行趨勢面擬合，再對剩余的誤差進行多面函數擬合，可以突出局部變化，擬合效果要優于直接使用多面函數進行擬合。

2)趨勢面擬合主要反映整體變化趨勢，當局部磁力異常觀測值變化顯著時，采用抗差趨勢面法可以減小對趨勢面擬合的不良影響。在多面函數擬合前，采用抗差估計理論進行質量控制，可以更有效剔除異常觀測值對趨勢面擬合的影響。

3)使用正交最小二乘多面函數法得到的擬合精度優于多面函數法，可以按照規則自適應地選擇特征點，提高了人工選擇特征點的效率。對系數矩陣進行正交化，不會影響最終的結果，因為正交化后并沒有參與多面函數系數的求解，僅是用于節點的選擇，因此可以作為一種自動選擇節點的參考方法。

1 趙建虎，等.基于多面函數的局域地磁場建模方法研究［J］.海洋通報，2009，28(4):89-97.(Zhao Jianhu，et al.Study on construction of local marine geomagnetic field model based on multi-surface function［J］.Marine Science Bulletin，2009，28(4):89-97)

2 劉兆平，楊進，武煒.地球物理數據網格化方法的選取［J］.物探與化探，2010，34(1):93-98.(Liu Zhaoping，Yang Jin and Wu Wei.The choice of gridding methods for geophysical data［J］.Geophysicalamp;Eochemical Exploration，2010，34(1):93-98)

3 張菊清，劉平芝.抗差趨勢面與正交多面函數結合擬合DEM數據［J］.測繪學報，2008，37(4):526-531.(Zhang Juqing and Liu Pingzhi.Combining fitting based on robust trend surface and orthogonal multiquadrics with application in DEM fitting［J］.Acta Geodaetica et Cartographica Sinica，2008，37(4):526-531)

4 楊元喜.抗差估計理論及其應用［M］.北京:八一出版社，1993.(Yang Yuanxi.The theory and application of robust estimation［M］.Beijing:Bayi Publishing House，1993)

5 楊元喜.自適應抗差最小二乘估計［J］.測繪學報，1996，25(3):206-211.(Yang Yuanxi.A daptively robust least squares estimation［J］.Acta Geodaetica et Cartographica Sinica，1996，25(3):206-211)

6 黃學功，等.地磁圖制備方法及其有效性評估［J］.北京航空航天大學學報，2009，35(7):891-895.(Huang Xuegong，et al.Geomagnetic mapping and validity estimation［J］.Journal of Beijing University of Aeronautics And Stronautics，2009，35(7):891-895)

STUDY ON CONSTRUCTION OF LOCAL MARINE GEOMAGNETIC FIELD MODEL BASED ON ORTHOGONAL LEAST SQUARE MULTI-SURFACE FUNCTION

Chang Yifeng，Chai Hongzhou and Wang Min
(Institute of Surveying and Mapping，Information Engineering University，Zhengzhou 450052)

Aim at the problem of quality control and node choice in modeling local marine geomagnetic field based on multi-surface function，a fitting method with combining robust trend surface and orthogonal least squares is proposed.In order to control the influence of some outstanding points to surface fitting，a robust fitting of the trend surface by using an equivalent weight is adopted and the adaptive node choosing method is proposed based on the effect of every node on the curve fitting calculated by using the orthogonal least squares as well.The results show that this method is more effective in accuracy and stability than normal method.

local marine geomagnetic field;robust estimate;orthogonal least square;multi-surface function;node

1671-5942(2012)03-0086-05

2011-11-09

常宜峰，男，1986年生，碩士研究生，主要從事測量數據處理理論與方法研究.E-mail:changyifeng1986@163.com

P207

A