注入法研究滲流特征

劉 冰，陳志明，蔡雨桐

（長江大學石油工程學院油氣鉆采工程湖北省重點實驗室，湖北武漢 430100）

注入法研究滲流特征

劉 冰，陳志明，蔡雨桐

（長江大學石油工程學院油氣鉆采工程湖北省重點實驗室，湖北武漢 430100）

流體在孔隙介質中以不同速度滲流時，分別遵循達西定律和福希海默定律。通過對注入法的研究，在等溫、不同壓力條件下測量滲流速度，引進了慣性系數，它的有效性也通過研究流體在燒結金屬孔隙介質中的滲流特征被證實。注入法這種新方法比常規的測量方法更優越，因為這個實驗只需兩分鐘就可以完成。并且消耗更少的氣體。根據速度的不同，將滲流過程分為兩個階段，其滲流規律分別滿足達西定律和福希海默定律。先用實驗數據計算達西定律范圍內滲流的滲透率，然后測定福希海默定律范圍內滲流的慣性系數，此方法測定的滲透率與真實值只有3%的誤差。并且它能確切的計算出滲流速度，而且很接近真實值。最后這個實驗需要挑選出一個特定的容器來保證實驗數據準確性。

孔隙介質；滲流速度特征；注入法；滲透率；慣性

大量的研究[1－4]表明當滲流流速足夠小時，流體通過多孔介質的滲流，遵循達西定律。當流速變得足夠的大。考慮到慣性的影響，福希海默定律可以描述流體流動狀態。達西基本定律可以成功的應用于可壓縮和不可壓縮流體滲流特征的描述。

Antohe[5]以及其他人，通過一個實驗可以用來計算被壓縮鋁制樣品的滲透率和慣性系數。這個實驗結果表明：考慮每一組數據來選配曲線可以得到更精確的結果。最近Belforte[6]等人通過實驗總結出：燒結的青銅孔隙介質的滲流參數，可以將測得的滲透率和慣性系數帶入福希海默方程來描述。然而，用目前存在的方法來做上述研究，需要在穩定流速的條件下來模擬，這會消耗大量的時間和能量；并且測試壓強和流速的實驗儀器必須調至合適范圍內來滿足測量需求，這樣會使實驗過程更加復雜。因此，盡管很多學者致力于多孔介質滲透率的測定，然而仍然需要找到一種方便有效的測定滲透率的新方法。

先前的研究[7]是用壓強回應法，即通過測定等溫容器[8]里的壓強變化，來間接地計算滲流速度。不過這種方法對于滲透率的測定并不適應。因為滲透率的測定必須在微小壓力梯度下才能進行。由于壓強傳感器分辨率的限制，通過壓強傳感器來獲得不同的精確壓強值就變得很困難。此外，流體滲流規律由服從達西定律變為服從福希海默定律逐漸過渡[9－10]，這個階段不像其他的部分只用一個壓力來區別兩種滲流狀態[11]。這個實驗中用一種可以準確測量壓強的壓強傳感器[12]（即后面提及的P.D.），使得測量過程更加方便，并且還減小了能量消耗。在這個研究中，用注入等溫容器的不同壓力值來計算滲透率、慣性系數和描述流速—壓力曲線圖。

1 理論模塊

由于通過多孔介質的流動很復雜（見圖1），以下面的假定作為理論基礎。（1）孔隙內部對于滲流的橫切面來說，孔隙所占各橫截面的比例與在空間內孔隙所占總體積比例是相同的；（2）在同一橫截面上流體的壓力、速度是相同的；（3）空氣通過孔隙介質流動過程中的溫度與室溫保持一致，在空氣和內部顆粒之間存在很大的空間，因此熱量交換很快，并且各個孔道相互連通，致使在沿著孔道延伸的方向，微小的滲流速度伴隨著空氣的密度改變，寫成如下形式：

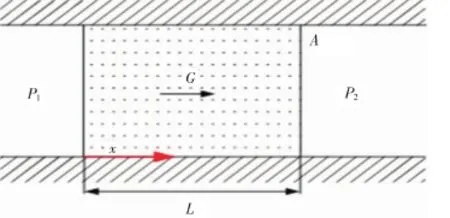
圖1 流體通過阻力元件的滲流簡圖

假設空氣是理想氣體，則密度可被表達為：

當滲流速度足夠小時，流體滲流阻力以粘滯力為主，并且與壓力梯度成正比，服從達西定律：

這個公式指出了流體在多孔介質中的基本滲流規律。當滲流速度較大時，流體的慣性成為了主導因素，福希海默定律考慮了慣性因素的影響，在達西定律的基礎上增加了一個二次因式。來描述滲流規律：

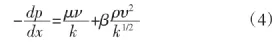
將（1）、（2）兩式帶入（3）式和（4）式，在臨界速度下，壓強對于位移長度進行積分:

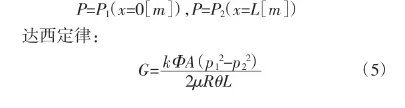
福希海默定律：

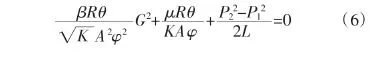
2 實驗儀器和流程

2.1 測量滲透阻力

選取一系列不同規格的多孔阻力元件（見圖2），標號為1#，2#，3#，和 4#。他們都是用SUS316L粉末在大約1000℃燒結而成的圓柱體。在燒結過程中，形成了結構復雜、相互連通的滲流孔道。

圖2 測量阻力元件

關于理論部分提到的孔隙度φ是由公式：

得出。γ＝8.03×103kg/m3是鋼鐵合金的密度，阻力元件的規模、質量和孔隙度（見表1）。

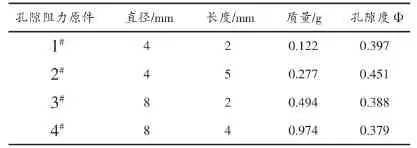
表1 所測阻力元件的尺寸、質量和孔隙度

2.2 穩態法

實驗流程（見圖3）。

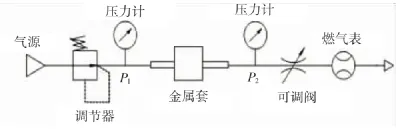
圖3 穩態法實驗裝置圖

將多孔阻力元件用一個環形合成橡膠密封在金屬圓柱桶里。壓縮的氣體從上游端注入，并且這個實驗裝置可調節注入壓力。兩個標有刻度的測壓儀器分別放置在實驗氣體流動的上游和下游，調節連通閥來改變下游氣體壓力。所有通過多孔阻力元件的氣體流量通過氣體測量儀測得，實驗過程中要停下來觀察時間和計算滲流速度。在壓力梯度變化很小的情況下還有一個額外用來測量壓強變化的傳感器KL17，其單位變化范圍是2 kPa。在實驗過程中實驗步驟如下：（1）保持氣體流速和注入壓力恒定；（2）調節閥連通閥來改變的值，并記錄相應的壓力和滲流速度值。

2.3 注入法

如圖4所示，是注入法的實驗儀器，是由供氣裝置，壓強調節器，平衡壓強的緩沖罐，一個螺旋閥門，一個等溫容器和一個P.D.組成。這個平衡壓強的緩沖罐的容積為30 L，安裝在壓強調節器之后，來穩定注入氣體的壓強，螺旋閥門作為注入氣體的開關。在等溫容器里填充銅絲，來為這個實驗提供等溫條件。當氣體流過P.D.傳感器時，不同的壓力值被直接測量出來。P.D.傳感器的分辨率是100 Pa/s。實驗儀器有三個容積不同的等溫容器（0.2 L，0.5 L和1.4 L）0.2 L的容器乘放1#和2#阻力元件，0.5 L的乘放4#阻力元件，1.4 L的乘放3#阻力元件。注入壓強被調節至584.9 kPa至488.2 kPa范圍內來進行實驗。這個注入的法比穩態法簡便，因為這個實驗不用逐點記錄實驗數據。首先，在等溫容器內大氣壓被設置為初始壓強，然后，打開螺旋閥讓氣體流過，通過一個16位的A/D板來獲得實驗數據，每10 s記錄一次實驗數據直至壓強恢復至初始設置的壓強。

在恒溫容器內的可壓縮流體的方程式可以寫為：

下述的方程式是由（8）式演化而來：

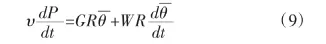
通過等溫容器測得壓強值，相應的滲流速度可以被計算出：

此注入法實驗加入一個P.D.，代替壓強傳感器來進行實驗，并且等溫容器內的壓強可以通過測量不同時間內dP/dt的值來獲得。

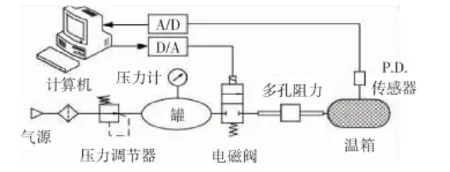
圖4 注入法實驗裝置圖

圖5 壓力—流速曲線圖（微小壓力梯度下）

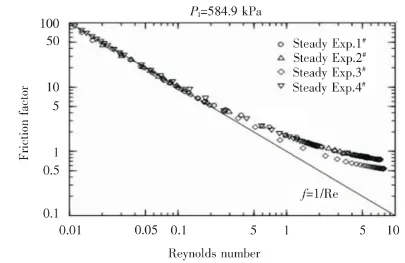
圖6 摩擦系數與雷諾數的聯系

3 結果與討論

3.1 實驗結果

在穩定狀態下，如圖5所示：當壓強每降低1P（1P=P1-P2），滲透率便相應地與壓降成比例的減小。并且在這個階段氣體滲流是適應達西定律的。

因此根據公式（5）通過幾組數據可以求得滲透率，將結果得出的滲透率帶入（6）來計算慣性系數。

滲透率的平方是多孔介質的度量：

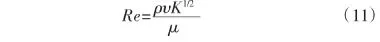
無量綱的摩擦因數被定義如下：

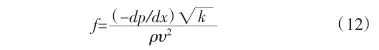
將（11）、（12）式帶入公式（4）得出如下公式：

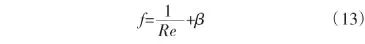
實驗的數據點顯示在圖6中。它表明，針對于此類標準的孔隙阻力元件，當雷諾數大于0.1時，滲流規律已經不遵循達西定律，此外摩擦因數會隨著雷諾數的增加而降低。當雷諾數足夠大時，滲流曲線趨于穩定，曲線的變化率，首先由滲透率決定，其次是慣性，而不是同時起作用。為了確保所測滲透率能很好地與達西定律相吻合，在很低的情況下，選擇出最優的慣性系數是合理的，就像Belforte等人的實驗[6]選擇出最優的壓強比。然而，即使這樣，忽略很多數據點也會導致很大的誤差。因此高斯-牛頓法求積公式，用于在考慮到所有數據的情況下，能得到精確的結果。對于注入法，用1#來做實驗，圖7根據注入氣體的時間將滲流速度劃分為兩部分，實驗表明，滲流速度會隨著時間不斷減小，直至氣體停止注入。

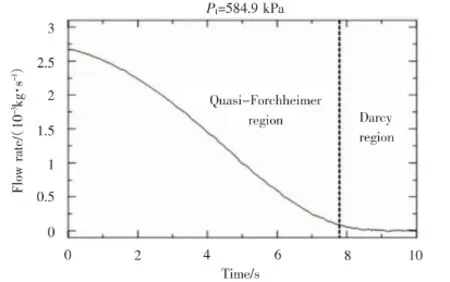
圖7 注入過程隨時間的變化圖（1#）

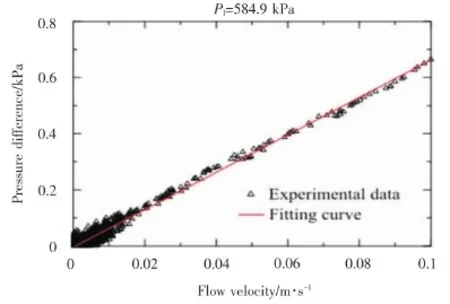
圖8 速度隨壓力變化曲線圖（1#）

多孔介質的滲流，流體本身的粘滯力對滲流速度起到了一定程度的限制作用。在注入氣體的過程中，氣體滲流從遵循福希海默定律逐漸向遵循達西定律過渡，當584.9 kPa時，實驗滲流速度為0.1 m/s，1#,2#,3#和 4#阻力元件對應雷諾數為 0.09，0.10，0.08，0.05，在圖7的曲線中，滲流速度被精確地分為兩部分，一個是適應達西定律的流速帶，其所對應流體的滲流速度是小于0.1 m/s，另一部分對應遵循福希海默定律的流速帶，其所對應的流體滲流速度是v>0.1 m/s，為了分別弄清楚滲透率k和慣性系數β，圖8所示滲流速度與壓強數據所擬合的曲線服從達西定律。當滲流速度趨近于零時，實驗數據點嚴重偏離擬合曲線。由圖來看，達西定律和福希海默定律所對應的合理流速界限是0.02 m/s。最優的慣性系數β是通過相同實驗步驟來設置相同滲流速度而得出來的。其實驗過程與穩態法一致。

實驗表明，滲透率在供給壓強不同時其值也會有所差異，慣性系數β隨著滲透率的變化，沒有呈現規律性的單調增長或減小的趨勢，因此，實驗結果表明，在滲透率和慣性系數之間不存在必要的聯系，兩者都是由多孔介質決定的。注入法的結果和傅常方程都是通過計算得出來的。注入法的實驗數據是通過放在等溫容器內的P.D.獲得的，這使得實驗結果能更好的與穩態法得到的數據資料相一致。注入法測量滲透率的效果更好，盡管所有的系數與穩態法所測得的值稍微有些偏差，但是計算的結果與穩態法的實驗結果大致相同，慣性系數β在高速度滲流過程中起主導作用，其微小的變化會引起滲流速度較大的改變。因此，慣性系數β被認為影響滲透率精確度的第三因素，表3提供了注入法和穩態法實驗的測量時間，氣體消耗量的比較情況。

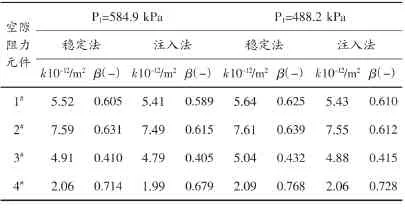
表2 通過穩態法和注入法給出的實驗數據

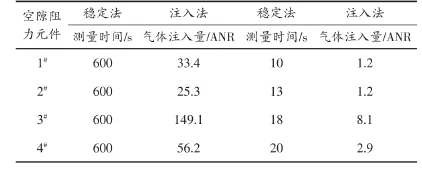
表3 兩種實驗方法所需時間和空氣消耗量的比較（P1=584.9 kPa）

分別取遵循達西定律和福希海默定律滲流范圍內的10組數據來評價穩態法的消耗。為了降低實驗的不確定性，使恒定流速維持30 s來獲得每組數據，另一方面，注入法的氣體消耗量等于流進等溫容器氣體的量。而且注入時間與測量時間看作相同。數據表明：注入法可明顯的減少測量時間和空氣消耗量。

3.2 流體可壓縮性的影響

當氣體通過多孔介質時，氣體的膨脹，使得滲流加速，因此空氣壓力、密度隨著滲流方向逐漸減小。氣體的可壓縮性，很大程度上影響了壓強和滲流速度之間的聯系。這可以從圖9得出，當壓力梯度小于5 kPa，氣體不能被壓縮的時候，所得出的實驗數據與達西定律很好地吻合，尤其藍色線是不可壓縮氣體所對應的實驗曲線，并且沿著滲流方向壓強是呈線性規律分布的。當壓力降較大時，紅色曲線是壓縮流體的實驗曲線，由于空氣的可壓縮性，使得滲流曲線是非線性的，并且因為不可忽略慣性的影響，導致曲線明顯偏離了可壓縮流體的理論數據。這個實驗的滲流規律遵循福希海默定律，而不是達西定律。通過觀察表明，考慮氣體可壓縮性，其滲流規律與不可壓縮流體所遵循的福希海默定律曲線相吻合。此外，這個實驗的注入過程是相對緩慢的。因此，它可以看作準穩態的過程。所以，可壓縮氣體在穩態和非穩態實驗中的結果是一樣的。

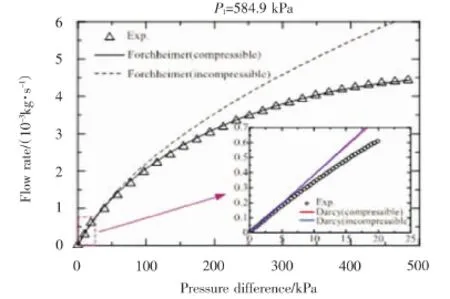
圖9 流速—壓力曲線圖（4#）

3.3 注入法容器的選擇

溫度在注入過程中會發生變化，它與注入的速度有關，而速度取決于容器的體積。所以在等溫條件下為了保證實驗測量的準確性，一定要控制好溫度的變化，因此適當的容器體積是必要的。這是通過在注入過程中觀察溫度的變化而證實的。圖4中所示的是實驗儀器裝置，3#阻力元件分別裝置在三個等溫容器內，壓強傳感器用來測量壓力，滲流過程中的溫度測量步驟如下：打開螺旋閥開始注入氣體，當測量容器溫度時停止注入，測量不同時間段的壓強和實驗停止時的壓強。當壓強穩定的時候，在容器內的溫度也恢復到了室溫，因此可以用下面的公式來計算某段時間段內的平均溫度：

在圖10中，顯示了壓強隨時間的變化關系，下圖顯示了溫度隨時間的變化情況。用0.2 L的等溫容器進行實驗時溫度波動最大值為3K，這會使測量滲流速度時產生較大的誤差，對于1.4 L的容器進行實驗時，溫度幾乎保持不變，經驗[15]得出結論Tp=VP1/（GmaxRθa），由公式可以看出：為使注入壓力恒定，注入時間應該保持3.5 s以上。如果等溫容器太大了單位時間內的壓強變化就不明顯了（在達西滲流定律范圍內）。實驗滲流速度從0.02 m/s變化到0.1 m/s來測量滲透率k，為了確保測量值足夠的準確，在速度0.02 m/s已經超出了P.D.分辨率情況下選擇最大容積來適應變化的壓強。

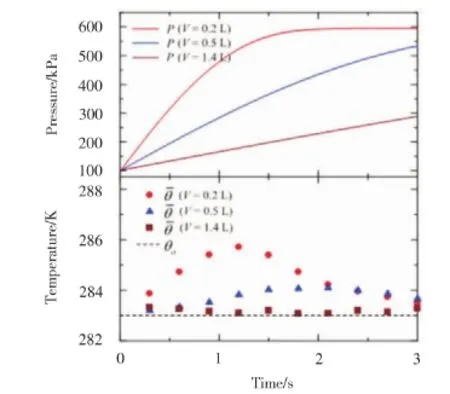
圖10 等溫容器內的溫度變化狀況

4 結論

在這篇文章中，當氣體注入到等溫容器時，通過P.D.傳感器得出的dP/dt，來計算滲流速度。達西、福希海默定律可以用來描述多孔介質的特征，包括粘性和慣性的影響。在注入的過程中滲流模式從適應福希海默定律逐漸過渡為遵循達西定律。達西定律和福希海默定律適應范圍的臨界滲流速度v=0.1 m/s。對于滲透率和慣性系數，要首先測定滲透率，然后是慣性系數，而不是同時測定。注入法比穩定法有更多優點，例如：測量時間短，消耗氣體少，這個被提出的實驗方法，滲透率測量的誤差為3%，這對于實際應用是足夠了。此外，對于等溫容器滲流的測量需要一個合理的注入速度，因此等溫容器的選擇要遵循不大不小的原則。

符號說明：

F：摩擦因數；P1：注入端壓力（Pa）；P2：流出端壓力（Pa）；R：氣體常（J/（kg·K））；V：等溫空間的體積（m3）；W：容器內空氣質量（kg）；G：滲流速度（m/s）；Gmax：最大滲流速（m/s）；P：絕對壓力（Pa）；β：慣性系數；μ：空氣粘度，（Pa·s）；ρ：空氣密度（kg/m3）；θ：溫度（K）；φ：孔隙度；θa：室溫（K）。

[1] Nield DA,Bejan A.Convection in porous media[J] .3rd ed.New York:Springer;2006.

[2] Liu JF,Wu WT,Chiu WC,Hsieh WH.Measurement and correlation of friction characte ristic of flow throug h foam matrixes [J] .ExperimentalThermaland Fluid Science 2006，30：329.

[3] Kim T,Lu TJ.Pressure drop through anisotropic porous medium like cylinder bundles in turbulent flow regime[J] .Journal of Fluids Engineering，ASME 2008，130：104501-1-5.

[4] Boomsma K，Poulikakos D.The effects of compression and pore size variations on the liquid flow characteristics inmetall foams[J] .Journal of Fluids Engineering，ASME 2002，124：263.

[5] Antohe BV,Lage JL,Price DC,Weber RM.Experimental determination of permeability and inertia coefficients of mechanically compressed aluminum porous matrices[J] .Journal of Fluids Engineering,ASME 1997，119：404.

[6] Belforte G,Raparelli T,Viktorov V,Trivella A.Permeability and inertial coefficients of porous media for air bearing feeding systems[J] .Journal of Teratology,ASME 2007，129：705.

[7] Kawashima K,Ishii Y,Funaki T,Kagawa T.Determination of flow rate characteristics of pneumatic solenoid valves using an isothermal chamber [J] .Journal of Fluids Engineering,ASME 2004，126：273.

[8] Kawashima K,Kagawa T,Fujita T.Instantaneous flow rate measurement of ideal gases[J] .Journal of Dynamic Systems，Measurement,and Control,ASME 2000，122：174.

[9] Andrade JS,Costa UMS,Almeida MP,Makes HA,Stanley HE.Inertial effects on fluid flow through disordered porous media[J] .Physical Review Letters 1999，82（26）：5249.

[10] Lage JL,Antohe BV,Nield DA.Two types of nonlinear pressure-drop versus flow-rate relation observed for saturated porous media[J] .Journal of Fluids Engineering,ASME 1997，119：700.

[11] ISO/CD 6358-3:determination of flow-rate characteristics of components using compressible fluid-part 3.2005.

[12] Kawashima K,Kato T,Yamazaki Y,Yanagisawa M,Kagawa T.Development of slit-type pressure differentiator using an isothermal chambe[rJ] .Measurement Science and Technology 2005，16：1150.

[13] Beavers GS,Sparrow EM.Non-darcy flow through fibrous porous media [J] .Journal of Applied Mechanics,ASME 1969，36：711.

[14] Beavers GS,Sparrow EM,Rodenz DE.Influence of bed size on the flow characteristics and porosity of randomly packed beds of spheres[J] .Journal of Applied Mechanics,ASME 1973，40:655.

[15] Kawashima K,Fujita T,Kagawa T.Flow rate measurement of compressible fluid using pressure change in the chamber[J] .Transactions of the Society of Instrument and Control Engineers 2001，E-1（1）：1－7.

Determination of flow rate characteristics of porous media using charge method

LIU Bing，CHEN Zhiming，CAI Yutong
（The Key Laboratory of Oil and Gas Drilling Extraction Project，College of Petroleum Engineering，Yangtze University，Wuhan Hubei 430100，China）

When liquid flow through porous media at different speeds,respectively follow the Darcy's law and Forchheimer’s law.Measuring seepage velocity under isothermal and different pressure through the research of injection,inertia coefficient being introduced,its effectiveness is confirmed through the study of fluids in sinter metal porous media seepage characteristics.This new injection method is more advantageousthan conventional measurement method,because this experiment takes only two minutes to complete.And it uses less gas.According to the different speeds,flow process is divided into two phases,respectively meet Darcy's law and the law of seepage Forchheimer’s law.Using experimental data flow within the calculation of Darcy's law of permeability and determination of Forchheimer’s law of inertia coefficient of flow in the context,this method for determination of permeability with real value only 3%error.And it can exactly calculate flow velocity,and is very close to the true value.Finally the experiment needs to pick out a specific container to ensure the accuracy of experimental data.

porous media；flow rate characteristics；charge method；permeability；Inertia

10.3969/j.issn.1673-5285.2012.11.002

TE312

A

1673－5285（2012）11－0005－07

2012-06-19

國家大學生創新實驗計劃項目（長江大學校發[2011] 55號）

劉冰，男（1989－），山東濰坊人，本科，現參與低滲透滲流規律方面的研究，郵箱：779836569@qq.com。