基于灰色關聯支持向量機的地表沉降預測

譚鵬，曹平

(中南大學 資源與安全工程學院，湖南 長沙，410083)

隧道的地表沉降量與眾多隨機性、不確定性因素存在著復雜的非線性關系，很難用一種確定的關系進行確定表達。如何用已經監測到的工程參數進行建模，并對沉降的未來演化規律、發展趨勢等進行預測，在工程上具有十分重要的意義[1]。目前主要方法是傳統分析方法、智能巖石力學的神經網絡方法和灰色理論。傳統分析方法是利用觀測的歷史沉降位移建立預測的統計模型，但是，這種統計模型一般當因變量和自變量之間是線性關系或一些簡單的函數關系時才使用，同時，當數據太少時不具有統計意義。智能巖石力學的神經網絡方法也是基于大樣本的一種學習方法。灰色理論在部分信息未知的小樣本、貧信息的系統預測中是一種非常有效的方法[2]，但近年來的研究表明[3?5]，該方法由于本身存在一些理論缺陷，使得預測結果出現較大誤差。在此，本文作者基于對巖石力學的研究思路[3?10]，將灰色關聯理論與基于統計學習理論發展的新學習方法支持向量機結合起來，將灰色理論中的灰色關聯分析應用到支持向量機模型中，充分應用支持向量機對復雜的非線性數據的預測能力[11]，建立灰色關聯支持向量機預測模型，以便為隧道地表沉降提供一種預測新途徑。

1 灰色關聯SVM預測模型

1.1 灰色關聯分析

灰色關聯分析[2](Grey relational analysis，GRA)的目的是定量地反映出系統與各影響因素的關聯度，進而從一個系統的眾多子因子中挑選出主因子。其方法是將系統中的因變因子所對應的統計數據轉化為幾何曲線，灰色關聯分析認為曲線幾何形狀越接近，則關聯程度就越大，該曲線所對應的因子即為主導此工程系統發展態勢的主要因子。灰色關聯計算步驟如下。

(1) 設系統的特征序列為：

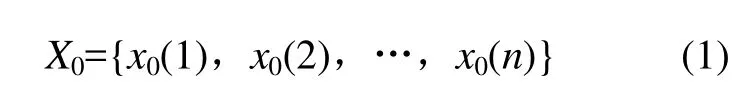
被比較序列為：

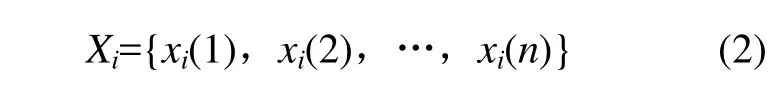
(2) 由于系統的眾多影響因子具有不同的量綱，在數量級上存在較大的差異，因此，為了盡量減少計算和分析過程中的誤差，對原始數據列采用均值化法或初值化法加以處理。

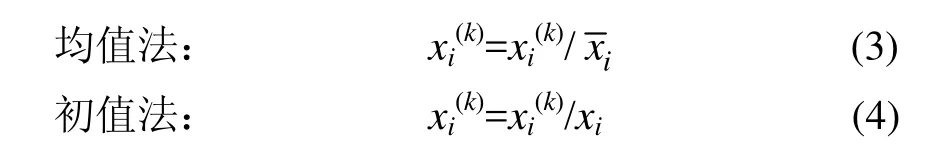
(3) 求解參考數列與被比較數列絕對差的最大值和最小值。灰色關聯度系數ε(k)按如下公式計算：

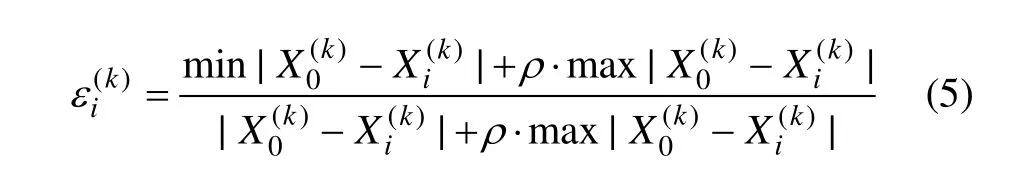
(4) 求解關聯度，并按照從大到小的順序依次排列關聯度，關聯度最大的為主要因子。

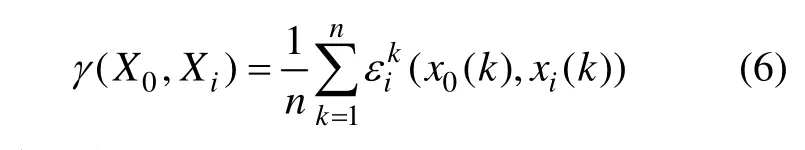
1.2 支持向量機理論

支持向量機[11](Support vector machine，SVM)是Vapink等根據統計學習理論中結構風險最小化原則提出的，具有很好的泛化性能。SVM既有嚴格的理論基礎，又能較好地解決小樣本非線性高維數和局部極小點等實際問題。用它建模不必知道因變量和自變量之間的關系，利用支持向量機空間中構造的最優決策函數，通過事先選擇的非線性映射將輸入樣本向量因子映射到高維特征空間，并在這個高維空間中，尋求獲得因變量和自變量之間非常復雜的非線性映射關系[4?5]，其核心思想就是學習機器要與有限的訓練樣本相適應。基本過程如圖1所示。

對于支持向量機函數擬合問題就是用函數f(x)=w·x+b 擬合數據{Xi，Yi}(i=1，2，…，n)，Xi∈Rn，Y∈R。數據樣本為n維向量的問題，按照支持向量機理論擬合函數為：

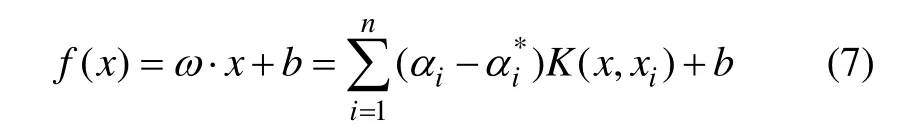
式中αi，αi*和b通過解下面的二次優化問題獲得：

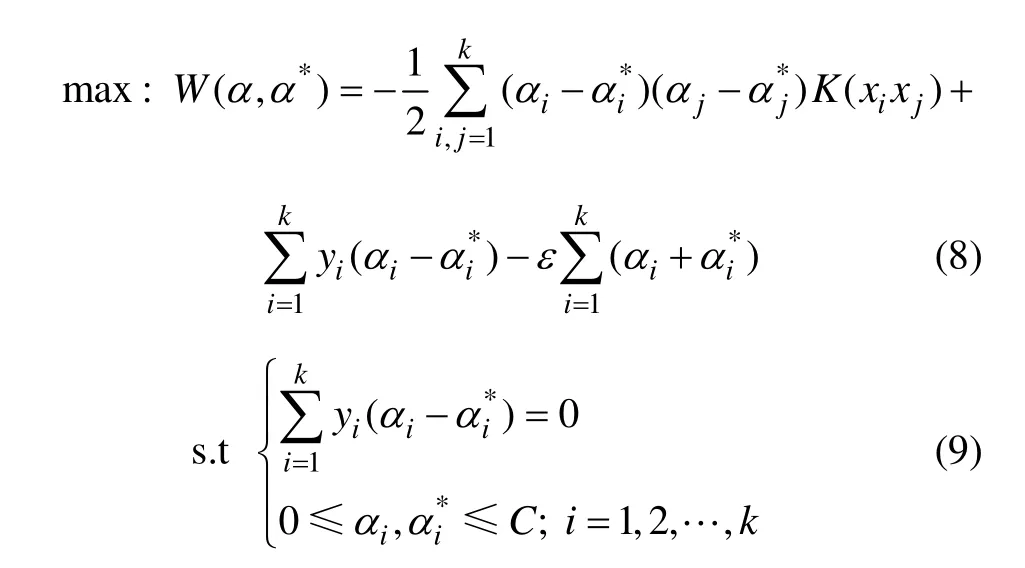
此時，通常αi和只有一小部分不為0，即為模型中的支持向量。式中：C為1個正常數；ε為懲罰因子，表示對超出誤差ε的樣本的懲罰程度；K(xi，xj)為核函數；對于非線性問題，若在原始空間中的得不到滿意的結果，則可以通過非線性變換轉化為某個高維空間中的線性問題。變換可能比較復雜，SVM通過引入核函數進行變換從而巧妙地解決了這一問題。核函數是通過非線性變換Φ把輸入空間Rn中的數據矢量x映射到1個高維特征空間F中。

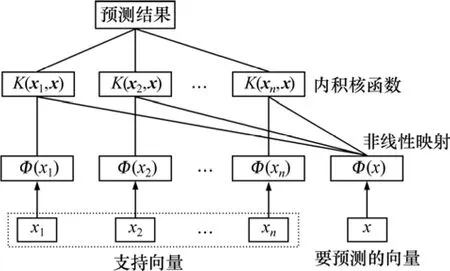
圖1 支持向量機結構示意圖Fig.1 Sketch of support vector mechine

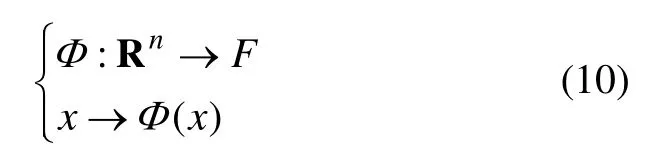
高維計算問題目前常用的核函數主要有以下幾種。

(1) 多項式函數：

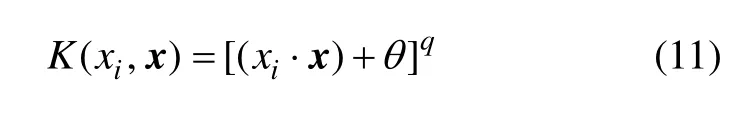
(2) RBF核函數：

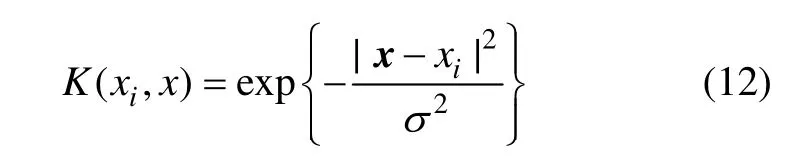
(3) Sigmoid核函數：

關于式(13)，(14)和(15)對應的二次優化問題，目前已有多種方法求解，在支持向量機問題中常用的方法有內點算法、SMO方法、分解方法等。

1.3 建模結構及參數的選擇

隧道的地表沉降受眾多復雜因素的影響，尤其是對樣本量和樣本有無規律都同樣適用的特點，為解決系統問題提供了可能性。掘進隧道引起的地表沉降系統是1個典型的灰色系統，影響最大沉降量H和沉降槽系數i的因子眾多，因此，可以根據灰色關聯分析原理，確定影響沉降的主要因子，消除無關因子的干擾，以此作為對支持向量機(SVM)輸入數據的前期處理，從而提高模型的預測能力。

本文是用模擬退火算法[10?11]來搜索 SVM 的最優的核函數 K(xi，xj)和參數 c。GR-SVM 預測模型結構圖見圖2。首先，初始化參數設置，隨機產生一組初始SVM參數，用給定的樣本訓練這一組由SVM參數所對應的模型；然后，用獲得的 SVM 模型對給定的檢驗樣本進行預測，以檢驗樣本中最大預測誤差作為適應值。通過模擬退火算法搜索迭代直到找到滿意的SVM 參數為止[10?11]。

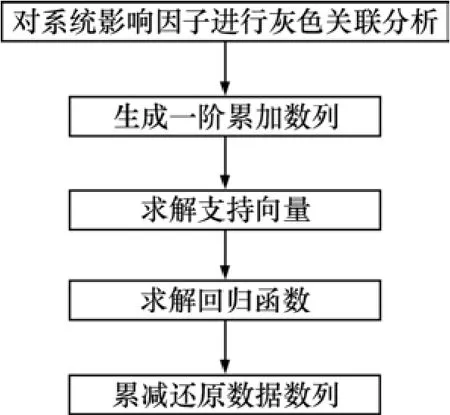
圖2 GR-SVM預測模型結構圖Fig.2 Sketch of GR-SVM’s prediction model

灰色關聯支持向量機模型首先用灰色關聯方法獲取主因子，然后，利用灰色預測方法對原始序列進行一次累加，生成一階累加序列。并利用支持向量機擬合非線性數據能力的優勢對生成序列建立預測模型，最后將預測結果進行累減還原得到預測值。

2 實例分析

本文依據文獻[12]中的實測資料建立GR-SVM預測模型。主要以3個場地的盾構工程為對象進行分析，包括上海地鐵二號線龍東路到中央公園盾構工程、廣州地鐵二號線越秀公園道三元里盾構工程、南京地鐵盾構工程。采用GR-SVM所得smax和i的預測值與實測值對比分別見表1和表2。地表沉降的GR-SVM訓樣品參數見表3和表4，其中：c為土層黏結力；H為隧道埋深；n為土的固結度；φ為內摩擦角；D為隧道直徑；F為盾構推力壓力；Es為割線彈模；P為注漿壓力值；v為盾構機推進速度。

選取26個施工監測點的實例，對地面最大沉降量Smax和沉降槽寬度系數i分別建立GR-SVM預測模型。隨機地選取20個監測點作為預測模型的學習樣本(見表3)，其余的6個樣本實例(表4)用于測試模型的預測能力。用學習樣本完成對GR-SVM模型的訓練，建立預測模型對剩余的6個樣本進行預測。

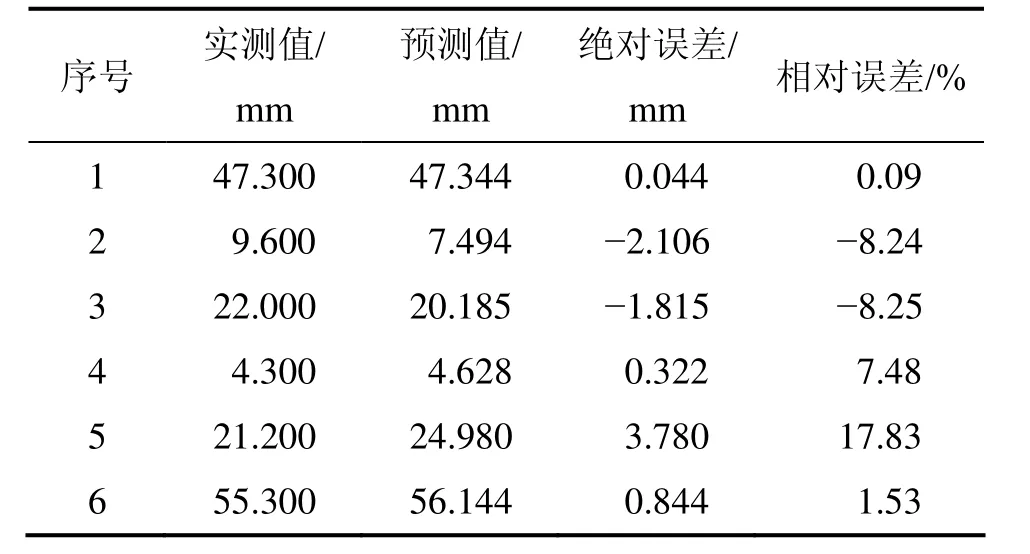
表1 smax預測值與實際值對比(GR-SVM)Table 1 Comparison between predicted and measured data of smax

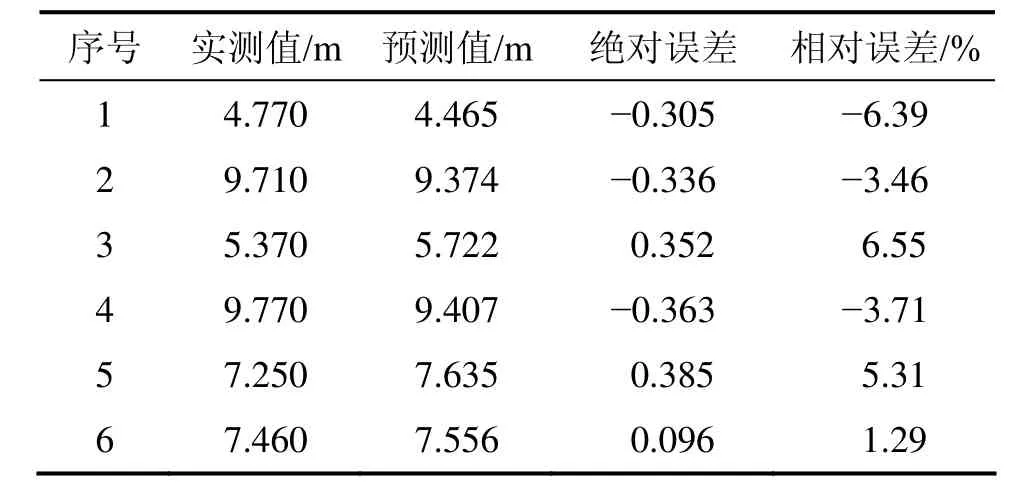
表2 i預測值與實際值對比(GR-SVM)Table 2 Comparison between predicted and measured data of i

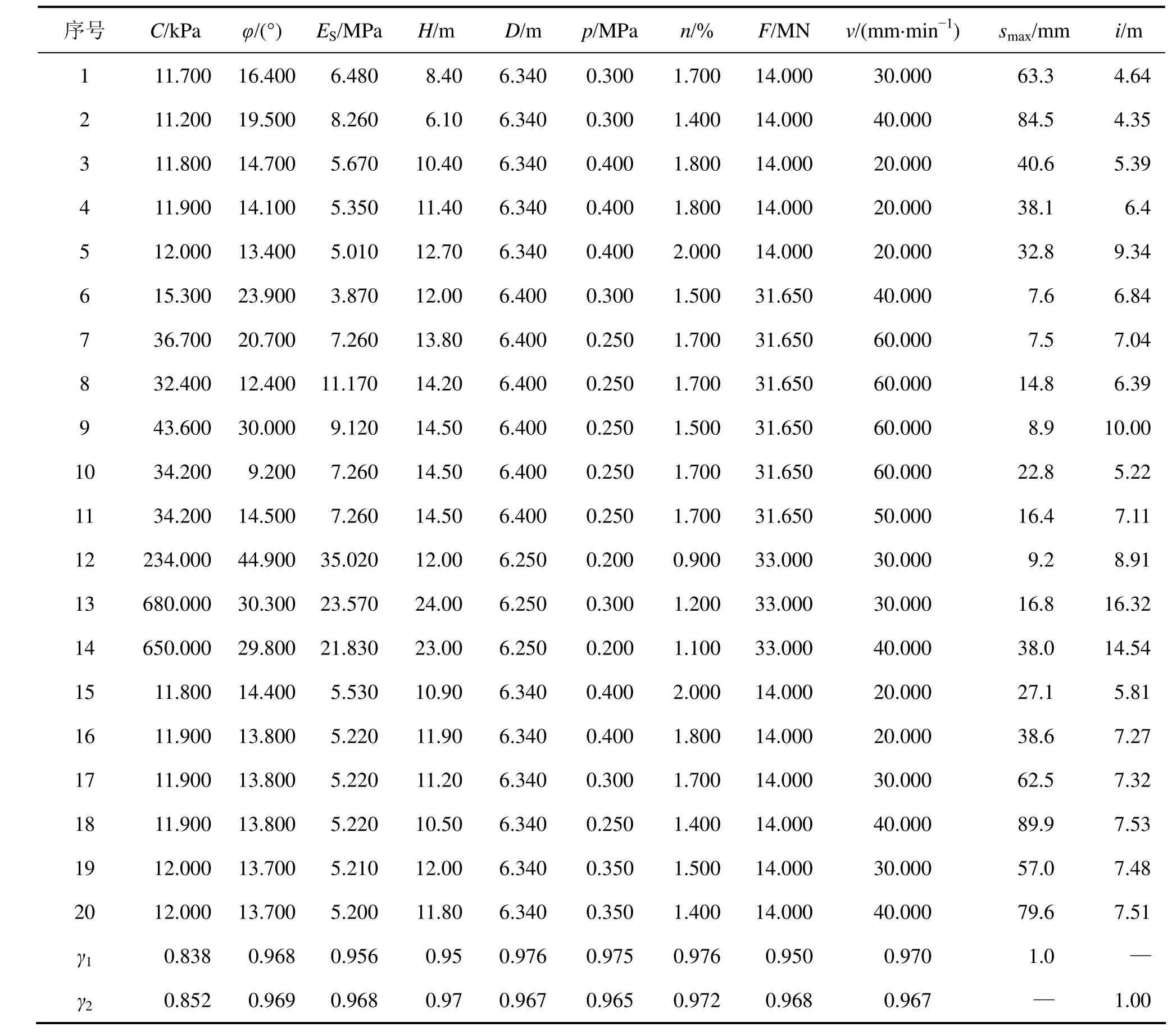
表3 地表沉降的GR-SVM訓練樣本參數Table 3 Learning samples for surface settlement

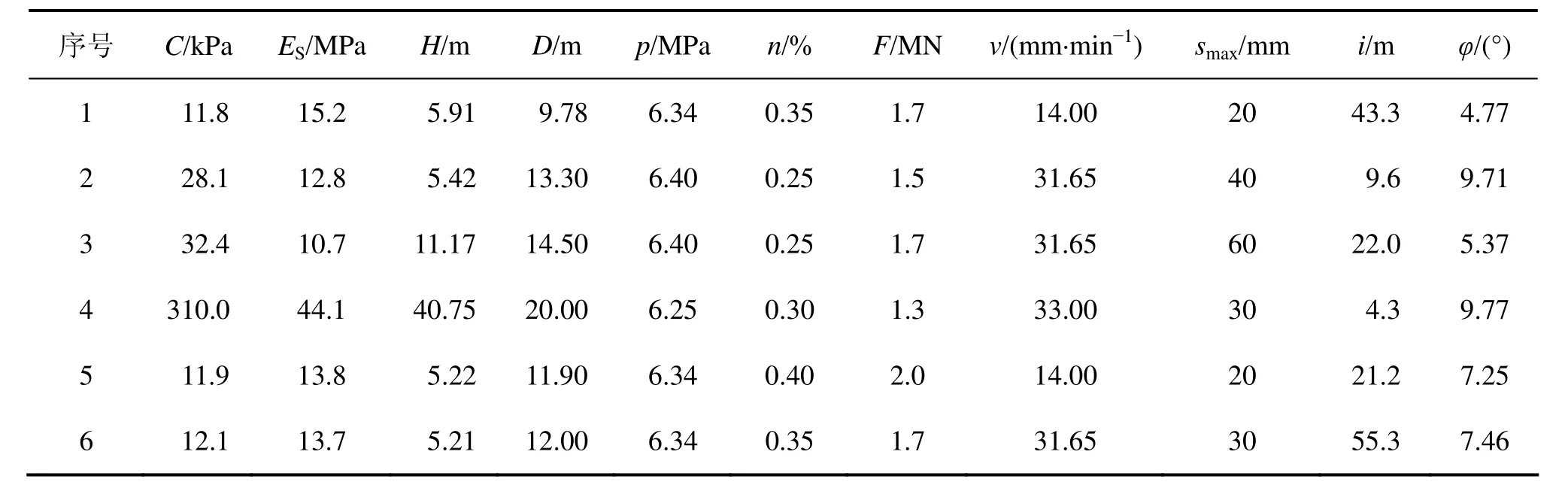
表4 地表沉降的GR-SVM訓練樣本Table 4 Prediction samples for surface settlement

建立灰色關聯分析模型選取主要影響因子。對特征序列和比較序列進行歸一化處理，并根據式(1)～(6)進行系統的特征序列和系統影響因素灰色關聯度分析，結果如表3所示。

3 結果分析

從表1和表2可知：smax預測值的最大絕對誤差的絕對值為3.780 mm，最大相對誤差為17.8%；i預測值最大絕對誤差的絕對值為 0.385 mm，最大相對誤差是6.55%；總體上具有較高的精度。

為了比較GR-SVM方法的預測精度，本文利用表3中的學習樣本選取 SVM 方法建立隧道地表沉降的預測模型。預測樣本通過GR-SVM和SVM 2種模型所得的預測誤差對比結果如表5所示。算法模型的精確度在很大程度上取決于所采用算法性能。為了便于采用量化的方法表示計算模型的性能，本文引入指標判識率(True accept rate，TAR)，即與實測值相符的預測值加以接收的正確概率。根據預測結果發現GR-SVM 的判識率達到 95%，SVM 的判識率只達70%，2種模型均能表達地表沉降的非線性關系。但由表 5比較 2種模型的預測誤差可以看出：基于GR-SVM 的隧道地表沉降的非線性組合預測精度更高，優于單一的 SVM 預測模型預測精度。表明灰色關聯支持向量機模型在合適的核函數等支持向量機參數下具有較高的預測精度。

在以上 2種模型的建立過程中均發現核函數K(xi，xj)和參數c對預測結果的影較大，因此，尋找一種合適的算法來搜索SVM的最優的核函數K(xi,xj)和參數 c，可以克服試算的低效率和盲目性。將模擬退火算法和支持向量機相結合，用模擬退火算法來搜索支持向量機參數[10?11]。smax和i的預測值與實測值對比結果分別見圖3和圖4。

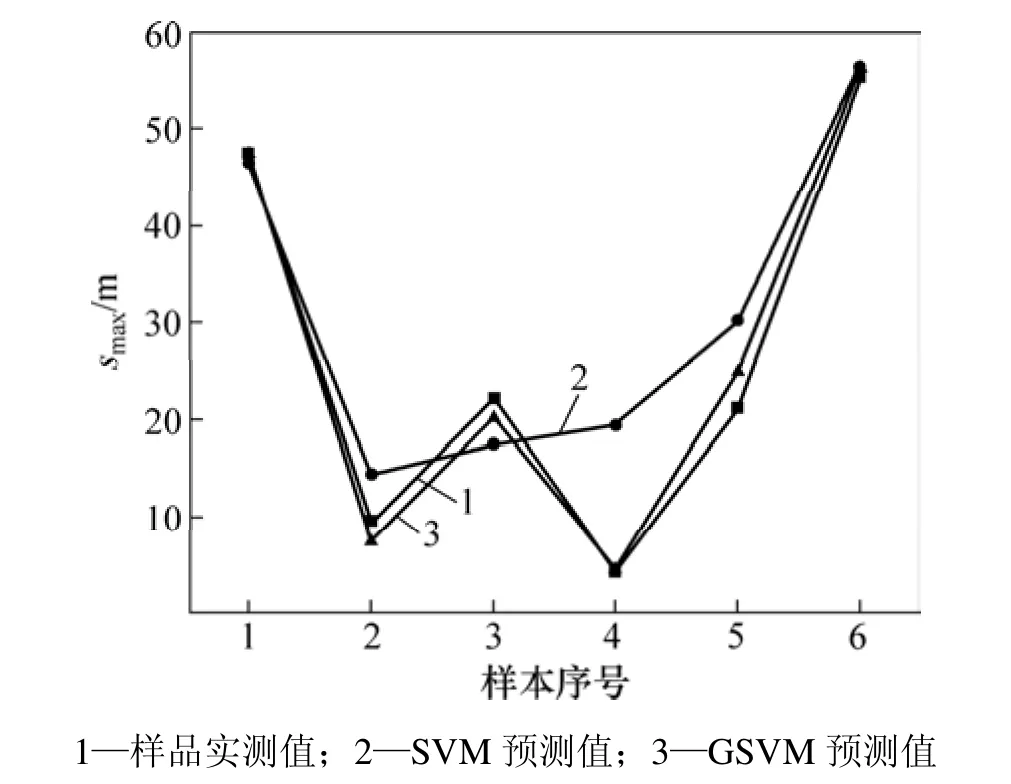
圖3 smax預測值與實際值對比Fig.3 Comparison between predicted and measured data of smax

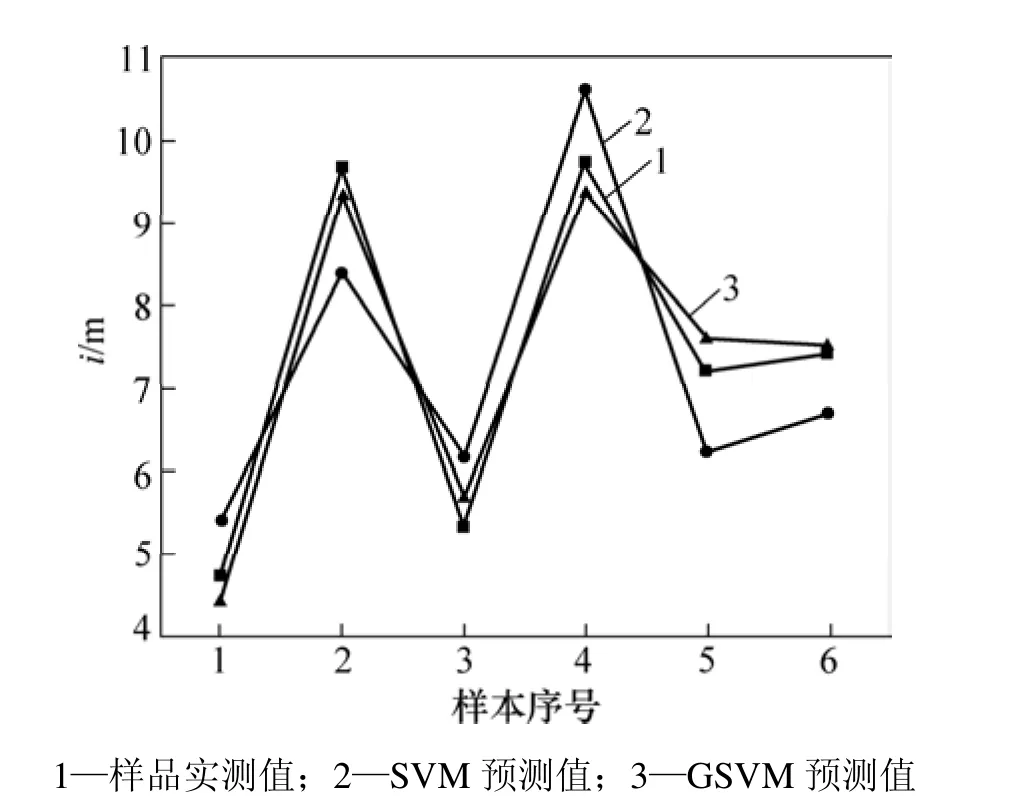
圖4 i預測值與實際值對比Fig.4 Comparison between predicted and measured data of i

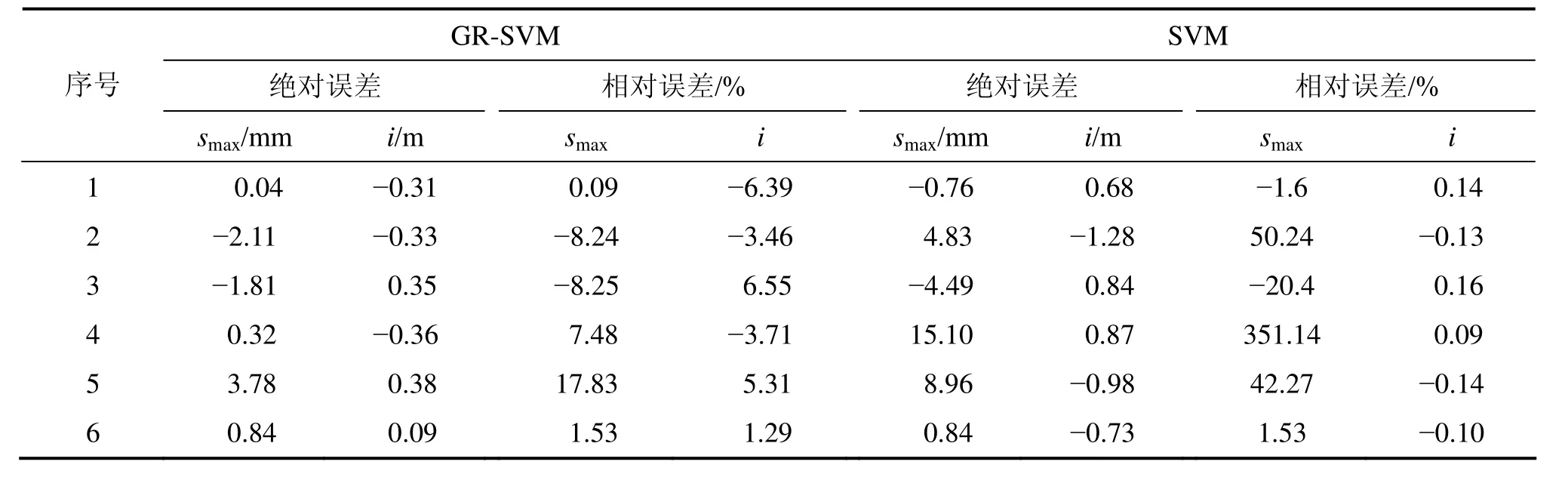
表5 測試樣本誤差Table 5 Error of test samples of surface settlement

4 結論

(1) 灰色關聯支持向量機的分析方法是對學習樣本數據和預測樣本數據進行關聯分析處理，并充分利用了SVM在處理高維數、非線性問題的優良特性。

(2) 用GR-SVM建立起巖土體力學參數與變形之間復雜的非線性映射關系，能夠較好地擬合預測復雜的地表沉降系統。該模型比較全面地反映了系統的變化特征，提高了對未來狀態分析的效率和預測精度。

[1]馮夏庭. 智能巖石力學導論[M].北京: 科學出版社, 2000:111?116.FENG Xia-ting. Introduce of intelligent rock mechanics[M].Beijing: Science Press, 2000: 111?116.

[2]陳新民, 羅國煜. 基于經驗的邊坡穩定性灰色系統分析與評價[J]. 巖土工程學報, 1999, 21(5): 638?641.CHEN Xin-min, LUO Guo-yu. Grey system analysis and evaluation of slop stability based on experience[J]. Chinese Journal of Rock Mechanics an Engineering, 1999, 21(5):638?641.

[3]林耀進, 周忠眉, 吳順祥. 集成灰色支持向量機預測模型研究與應用[J]. 計算機應用, 2009, 29(12): 3287?3289.LIN Yao-jin, ZHOU Zhong-mei, WU Shun-xiang. Research and application of integrated grey support vector machine model[J].Journal of Computer Applications, 2009, 29(12): 3287?3289.

[4]趙洪波, 馮夏庭. 非線性位移時間序列預測的進化?支持向量機方法及應用[J]. 巖土工程學報, 2003, 25(4): 468?471.ZHAO Hong-bo, FENG Xia-ting. Study and application of genetic-support vector machine for nonlinear displacement time series forecasting[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(4): 468?471.

[5]趙洪波, 馮夏庭. 位移反分析的進化支持向量機研究[J]. 巖石力學與工程學報, 2003, 22(10): 631?633.ZHAO Hong-bo, FENG Xia-ting. Study of geneticsupport vector machine in displacement back analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10): 631?633.

[6]景海河, 葉欣. 基于支持向量機的礦區開采沉降的預測[J].黑龍江科技學院學報, 2008, 18(4): 250?252.JING Hai-he, YE Xin. Subsidence prediction of diggings based on support vector machine[J]. Journal of Heilongjiang Institute of Science & Technology, 2008, 18(4): 250?252.

[7]徐傳華, 任青文, 周慶華. 基于支持向量機和模擬退火算法的位移反分析[J]. 巖石力學與工程學報, 2005, 24(22):4134?4138.XUN Chuan-hua, REN Qing-wen, ZHOU Qing-hua.Displacement back analysis based on support vector machine and simulated annealing[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22): 4134?4138.

[8]Kirkpatrick S, Gelatt C D, Veccki M R. Optimization by simulated annealing[J]. Science, 1983, 220: 67l?680.

[9]趙洪波, 馮夏庭. 支持向量機函數擬合的邊坡穩定性估計[J].巖石力學與工程學報, 2003, 22(2): 241?245.ZHAO Hong-bo, FENG Xia-ting. Application of support vector machines function regression in the evolution stability of slope[J]. Chinese Journal of Rock Mechanics and Engineering,2003, 22(2): 241?245.

[10]趙洪波. 支持向量機在隧道圍巖變形預測中的應用[J]. 巖石力學與工程學報, 2005, 24(4): 649?652.ZHAO Hong-bo. Predict the surrounding deformations of tunnel using support vector machine[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(4): 649?652.

[11]Cristianini N, Taylor S T. 支持向量機導論[M]. 李國正, 王猛,譯. 北京: 電子工業出版社, 2004: 81?129.Cristianini N, Taylor S T. An introduction to support vector machines and other kernel-based learning methods[M]. LI Guo-zheng, WANG Meng, transl. Beijing: Electronics Industry Press, 2004: 81?129.

[12]李守巨, 劉應曦, 孫偉. 智能計算與參數反演[M]. 北京:科學出版社, 2008: 145?274.LI Shou-ju, LIU Ying-xi, SUN Wei. Intelligence computation and parameter identification[M]. Beijing: Science Press, 2008:145?274.