高階橢圓錐齒輪齒形設計與加工

林 超 龔 海 侯玉杰,2 聶 玲

1.重慶大學機械傳動國家重點實驗室，重慶，4000442.中國人民解放軍96263部隊，洛陽，471500

0 引言

非圓錐齒輪是用來傳遞兩相交軸之間非勻速比運動的，它結合了非圓齒輪與圓錐齒輪的特點，具有體積小、運動平穩、傳動效率高等優點[1]。非圓錐齒輪現在主要用在一些特殊的傳動場合，如非圓錐齒輪限滑差速器、非圓錐齒輪變量泵等。隨著對非圓錐齒輪研究的深入，這一新型的傳動形式必然會應用到更多的場合，這就對非圓錐齒輪的設計、加工制造提出了進一步的要求。

齒形的設計是齒輪傳動設計中一個重要的方面，齒形設計的優劣，關系到齒輪副是否可以按照預定的傳動比進行傳動，以及齒輪副嚙合情況的好壞。非圓錐齒輪齒形設計尤為復雜，其中趙玉民等[2]、Xia等[3]根據不同的理論各自提出了非圓錐齒輪齒形設計的方法。本文基于傳統的齒輪范成法原理來設計非圓錐齒輪的齒形。

非圓錐齒輪加工是限制其應用的主要瓶頸，目前在國內外，針對非圓錐齒輪的加工尚未提出很好的解決方法，相關研究還處于探索階段[4-5]。CNC技術的日趨成熟和普及，特別是五軸聯動數控機床的出現，很好地解決了復雜曲面的加工問題，且五軸聯動數控機床加工精度高，這為非圓錐齒輪的加工制造提供了新的途徑。

1 基本原理

橢圓錐齒輪副是一種典型的非圓錐齒輪傳動形式，當將橢圓錐齒輪的極角縮小整數倍，就可演變出相應的高階橢圓錐齒輪副，即對應演變成二階橢圓錐齒輪副、三階橢圓錐齒輪副、…、n階橢圓錐齒輪副[6]。高階橢圓錐齒輪的節錐面方程如下：

(1)

式中，n為主動輪的階數；k為主動輪的偏心率；θ為高階橢圓錐齒輪的周轉角。

高階橢圓錐齒輪實現的傳動比為

(2)

1.1 高階橢圓錐齒輪齒廓形成原理

由齒輪空間嚙合原理可知，當高階橢圓錐齒輪副傳動時，兩高階橢圓錐齒輪的節錐面做相切純滾動，若把其中一個高階橢圓錐齒輪換成刀具(標準的圓錐齒輪)，此時兩者的傳動表現為高階橢圓錐齒輪的節錐面與圓錐齒輪刀具的節錐面做相切純滾動。在嚙合過程中，刀具的齒廓將會包絡出與其具有相同漸開線形狀的齒廓，這樣即可獲得高階橢圓錐齒輪的齒形。

由上述原理可得到高階橢圓錐齒輪在采用范成法進行加工的過程中，各運動參數之間的關系以及高階橢圓錐齒輪齒形的生成過程。建立范成加工的坐標系，如圖1所示，三維笛卡兒坐標系OXYZ的原點位于O點，Z軸豎直向上，Y軸水平向右；高階橢圓錐齒輪的錐頂與原點O重合，高階橢圓錐齒輪的回轉中心軸與Z軸重合；刀具的自回轉中心軸為OO1，在初始位置時，刀具的節曲線與高階橢圓錐齒輪的節曲線相切于點M，OM與Z軸正方向夾角為ρ0；刀具節曲線相切于高階橢圓錐齒輪的節曲線并做純滾動，刀具繞Z軸轉過角度θ1時，如圖1所示，此時刀具節曲線與高階橢圓錐齒輪的節曲相切于點M′,刀具的回轉中心軸為OO′1，切線OM′與Z軸正方向夾角為ρ1。

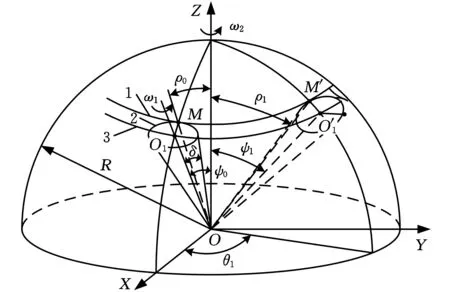
1.高階橢圓錐齒輪的節曲線 2.刀具節曲線3.刀具移動軌跡圖1 范成加工的坐標系

圖1中，δ為圓錐刀具的節錐角。

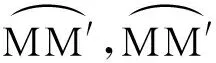
(3)

式中，R為高階橢圓錐齒輪的球面半徑。

刀具繞自身旋轉軸轉過的角度：

(4)

由圖1知，ψ0=ρ0+δ，ψ1=ρ1+δ，刀具繞Y軸旋轉的角度θy為

θy=ψ1-ψ0=ρ1-ρ0

(5)

綜合式(4)、式(5)，可以確定范成加工過程中，高階橢圓錐齒輪與刀具范成運動時的運動變化關系如下：

(6)

根據以上齒廓成形原理，在Solidworks中利用其應用程序接口(API)，開發高階橢圓錐齒輪參數化仿真范成加工程序，運行結果如圖2所示。

(a)二階 (b)三階(c)四階圖2 高階橢圓錐齒輪包絡齒廓

1.2 高階橢圓錐齒輪齒面方程

根據上述高階橢圓錐齒輪齒廓生成原理，由空間幾何關系，利用解析法可以推導得到高階橢圓錐齒輪的齒面方程。

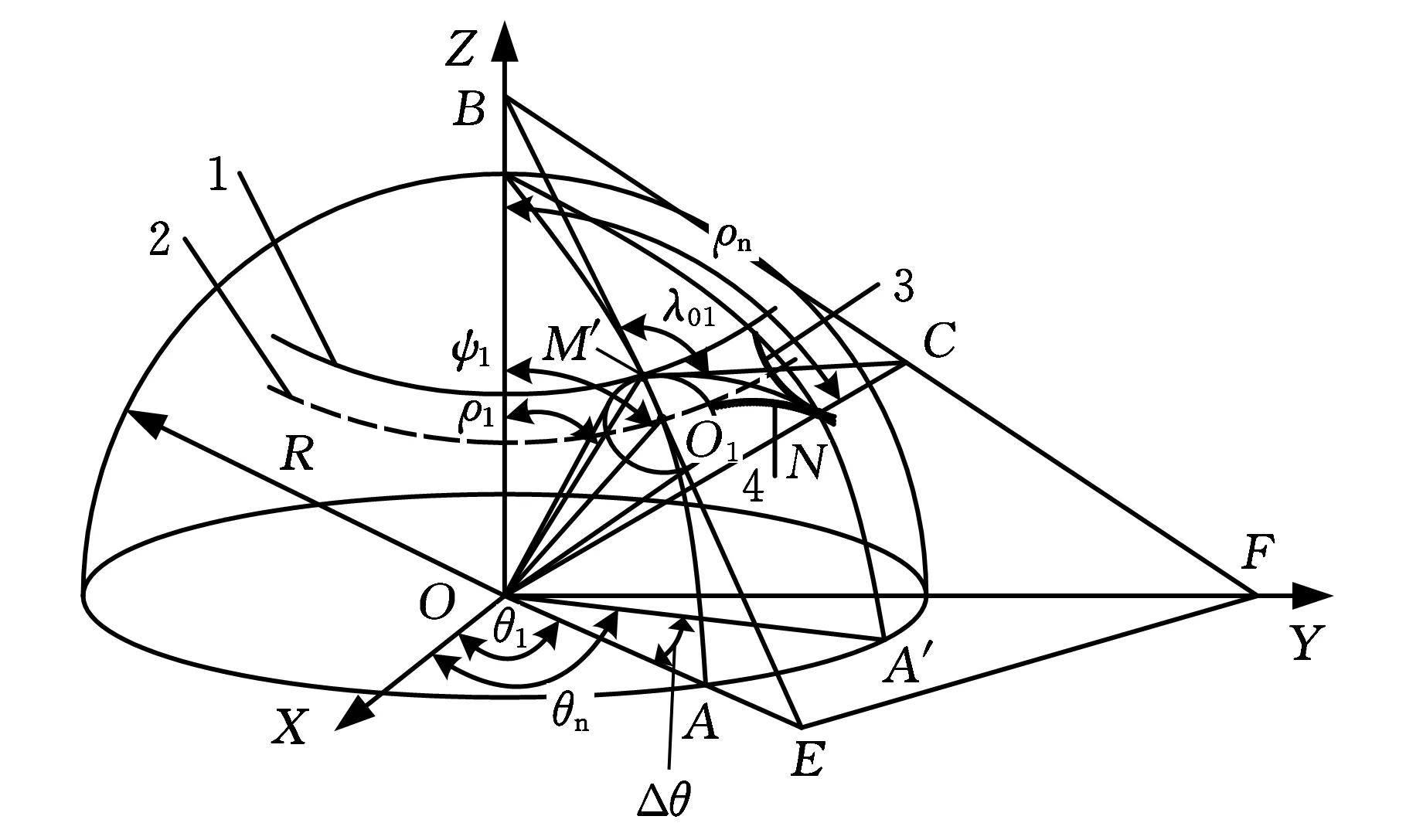
1.高階橢圓錐齒輪的節曲線 2.刀具移動軌跡3.高階橢圓錐齒輪齒廓 4.刀具齒廓圖3 齒面的形成

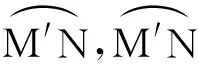
在圖3所示的位置，刀具節曲線在高階橢圓錐齒輪節曲線滾過的弧長所對應的圓心角ψ為[7]

(7)

α=arcsin(sinψcosαn)

(8)

M′B與M′C的夾角λ01為

(9)

刀具齒廓與高階橢圓錐齒輪的齒廓相切于點N,ON與Z軸的夾角ρn為

ρn=arccos(cosρ(θ1)cosα+sinρ(θ1)sinαcosλ01)

(10)

ON在XY平面的投影OA′與OO′1在XY平面的投影OA的夾角Δθ為

(11)

則綜合式(10)、式(11)，可得到高階橢圓錐齒輪左上齒廓方程為

(12)

其中，θn為OA′與X軸正向的夾角。

根據齒廓點所在的位置，將高階橢圓錐齒輪的齒廓分為：左邊位于齒頂曲線與節曲線之間的左上齒廓；左邊位于齒根曲線與節曲線之間的左下齒廓；右邊位于齒頂曲線與節曲線之間的右上齒廓；右邊位于齒根曲線與節曲線之間的右下齒廓。M′B與M′C的夾角因齒廓點所在的位置不同取值會有所不同，當齒廓點分別在左上齒廓、左下齒廓、右上齒廓、右下齒廓時，對應M′B與M′C的夾角分別為λ01、λ02、λ11、λ12，且λij(i=0,1；j=1,2)對應取值分別為

(13)

ζ2=arctan(tanαnsecψ)

同理可得高階橢圓錐齒輪的左下齒廓、右上齒廓、右下齒廓方程，綜合得高階橢圓錐齒輪的齒廓方程

(14)

1.3 高階橢圓錐齒輪的幾何設計

1.3.1高階橢圓錐齒輪的齒數Z1

在高階橢圓錐齒輪傳動過程中，輪齒的布局通常是將長軸端布置成齒槽，短軸端布置成輪齒。此時一對共軛齒輪的輪齒是對稱分布的，輪齒嚙合過程的受力狀態可得到改善，且方便于設計及加工制造。此時高階橢圓錐齒輪的齒數Z1須滿足如下方程：

Z1=(2ε+1)n

(15)

式中，ε為正整數。

在設計過程中可根據實際的受力情況，確定正整數ε，從而確定高階橢圓錐齒輪的齒數Z1。

1.4統計學方法采用SPSS21.0統計學軟件對數據進行統計分析。計量資料以均數±標準差(±s)表示,采用t檢驗;計數資料以率(%)表示,采用X2檢驗。P<0.05表示差異具有統計學意義。

1.3.2高階橢圓錐齒輪的球面半徑R

由上述高階橢圓錐齒輪的齒廓生成過程可知，高階橢圓錐齒輪的球面半徑R與圓錐刀具的球面半徑R′相等，則可由圓錐刀具的基本參數確定高階橢圓錐齒輪的球面半徑R。

由齒輪嚙合原理可知，圓錐刀具與高階橢圓錐齒輪范成時，它們一個齒在節錐面上展開所對應的弧長必須相等，即可以得到方程：

(16)

式中，Z0為圓錐刀具的齒數。

由于式(16)中有Z0、δ兩個未知數，則可以取定齒數Z0來求出節錐角δ，也可以取定節錐角δ來求出齒數Z0。同時，由于刀具其自身也要滿足不發生根切的條件，其齒數Z0>17cosδ。

確定圓錐刀具的齒數和分錐角后，可由圓錐齒輪的尺寸計算公式得到圓錐刀具的球面半徑R′：

(17)

從而可得高階橢圓錐齒輪的球面半徑R：

(18)

1.3.3高階橢圓錐齒輪的齒寬B

由于高階橢圓錐齒輪是一種新的錐齒輪傳動形式，該種齒輪的齒寬B尚沒有通用的計算公式，在此可借鑒圓錐齒輪的齒寬B的計算公式：

(19)

在設計和實際加工過程中，由式(19)求得齒寬B后，進行圓整，再根據實際受力情況進行調整。

1.4 高階橢圓錐齒輪實體模型建立

在Solidworks中，利用其三維造型功能以及應用程序接口(API)，根據上述所提出的高階橢圓錐齒輪齒形的設計方法，開發出高階橢圓錐齒輪實體建模的程序，建立高階橢圓錐齒輪副的虛擬實體及其裝配模型，如圖4所示。

(a)二階

(b)三階

(c)四階圖4 高階橢圓錐齒輪實體模型及裝配體

2 五軸聯動數控銑床加工過程

2.1 五軸聯動數控銑床

高階橢圓錐齒輪的加工，選用的是五軸聯動數控銑床，銑床型號為SmartCNC500，其工作部分結構如圖5所示，基本參數見表1。在銑床上共有5個數控軸實現復雜曲面的加工，可以把其運動軸分為刀具的運動軸和工件的運動軸。刀具運動軸包括沿X軸方向的平移運動Xt、沿Y軸方向的平移運動Yt及沿Z軸方向的平移運動Zt等三個平動軸；工件的運動軸由沿Z軸方向的旋轉運動Zr和沿Y軸方向的旋轉運動Yr兩個旋轉軸組成。

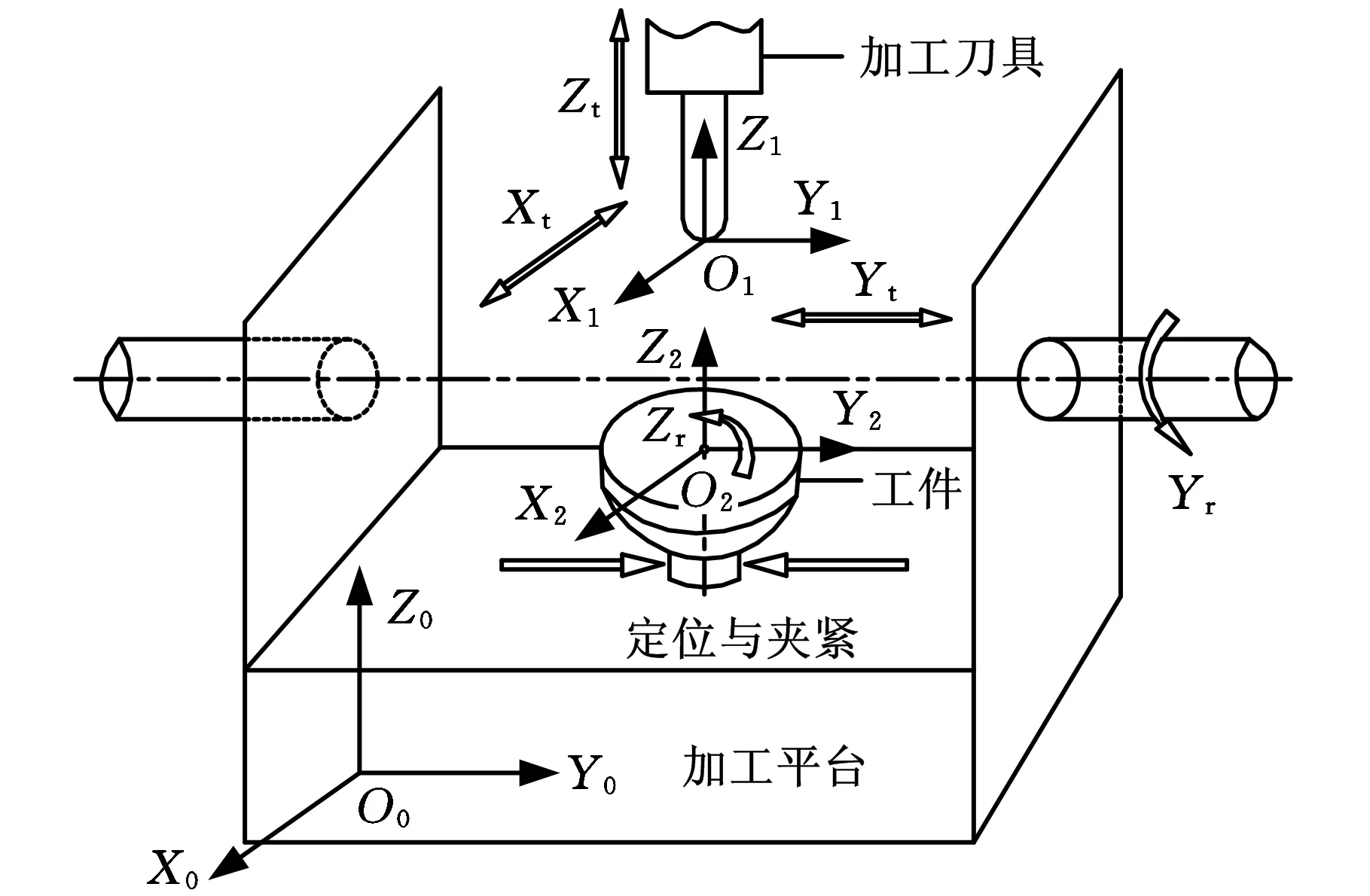
圖5 五軸聯動銑床結構與加工坐標系

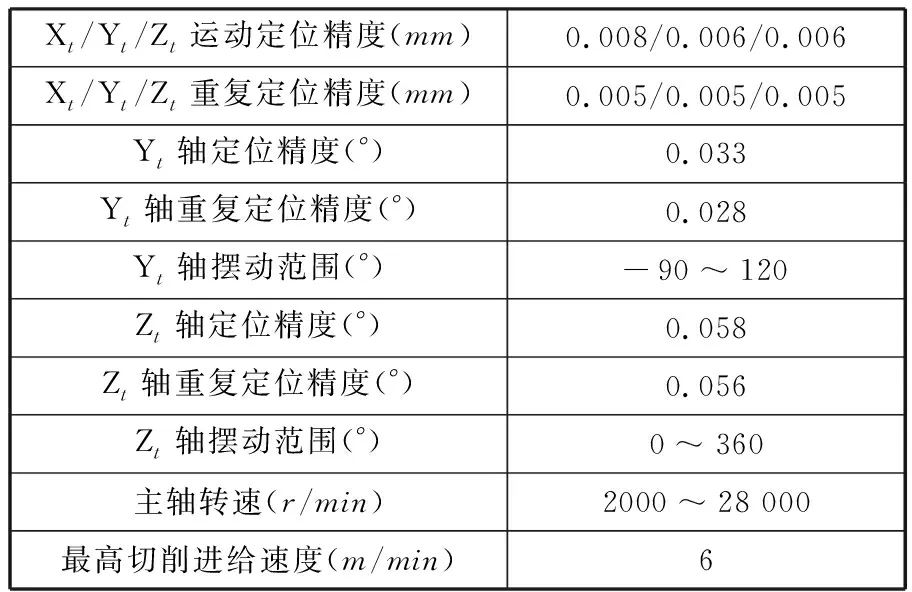
表1 五軸聯動數控銑床基本參數表

2.2 五軸聯動數控銑床的坐標系

如圖5所示，建立銑床的固定全局坐標系O0X0Y0Z0、刀具坐標系O1X1Y1Z1(與刀具固連)、工件坐標系O2X2Y2Z2(與工件固連)。設初始位置時，三坐標系完全重合在銑床坐標系O0X0Y0Z0上。開始加工后，刀具坐標系O1X1Y1Z1在全局坐標系O0X0Y0Z0中沿X軸、Y軸及Z軸移動的距離分別為x、y、z，即刀具在銑床坐標系O0X0Y0Z0中平移的坐標為(x,y,z)。同時，由于工件的旋轉，工件坐標系O2X2Y2Z2先繞其Z2軸旋轉角度γ，再繞其Y2軸旋轉角度η，由于工件坐標系O2X2Y2Z2只做旋轉運動，全局坐標系原點O0X0Y0Z0和工件坐標系原點O2X2Y2Z2是完全重合的。

2.3 加工過程

由以上分析可得，刀具坐標系變換到銑床坐標系的變換矩陣為

(20)

即刀具在全局坐標系O0X0Y0Z0下的坐標為

(21)

工件坐標系變換到全局坐標系O0X0Y0Z0的變換矩陣為

(22)

即工件在全局坐標系O0X0Y0Z0下的坐標為

(23)

由式(21)～式(23)可得，刀具坐標系變換到工件坐標系的變換矩陣為

(24)

由以上的坐標變換關系，即可建立起數控加工時刀具與工件之間的位置變化關系。

毛坯加工完成后，依據以上提出的加工銑床及其坐標變換分析，編制加工所需的數控程序，即可進行高階橢圓錐齒輪的加工。本次加工包括粗加工、半精加工和精加工三個程序。圖6所示為各個齒輪加工過程圖及獲得的二階、三階、四階橢圓錐齒輪樣件，粗加工只需三軸聯動即可完成，所以加工過程中只有刀具坐標系相對于機床坐標系的平移運動坐標變換。半精加工和精加工則必須采用五軸聯動加工，此時除了刀具坐標系相對于銑床坐標系有平移坐標變換外 ，還包括工件坐標系相對于銑床坐標系的旋轉坐標變換。

(a)二階

(b)三階

(c)四階圖6 加工過程與高階橢圓錐齒輪

2.4 對滾檢查

高階橢圓錐齒輪運動檢查，是將加工所得到的二階、三階、四階橢圓錐齒輪，在對滾檢查機上進行對滾檢查試驗，如圖7所示。檢查試驗結果表明，采用本文方法加工出來的高階橢圓錐齒輪副的嚙合接觸線軌跡接觸良好，能夠在全齒厚方向上全接觸滾動。驗證了范成法生成高階橢圓錐齒輪齒廓模型的正確性，以及五軸數控精銑加工方法的可行性。

圖7 對滾試驗

2.5 嚙合試驗

高階橢圓錐齒輪傳動的試驗臺由一臺變頻直流電動機、變頻控制器、轉速扭矩傳感器、位移傳感器、聯軸器、高階橢圓錐齒輪傳動箱、試驗臺架、計算機及數據采集處理軟件等儀器及設備組成。二階橢圓錐齒輪傳動試驗臺如圖8所示。

圖8 二階橢圓錐齒輪傳動試驗臺

為測試轉速，在輸入/輸出軸上分別安裝了轉速扭矩傳感器。通過轉速扭矩傳感器測出輸入/輸出軸的轉速，其比值即為所測傳動比。依據搭建好的試驗平臺和制訂的試驗方案進行試驗數據的測量和采集。將采集得到的數據經數據處理，即可獲得二階橢圓錐齒輪的試驗傳動比與理論傳動比的對比結果，如圖9所示。

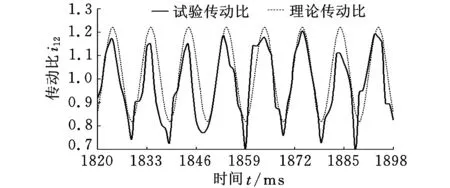
圖9 傳動比試驗值與理論值對比

由圖9可知，忽略加工制造誤差、試驗臺的安裝誤差以及測量環境中一些不確定因素的影響，試驗傳動比曲線與理論傳動比曲線相當吻合，表明了本文建立的高階橢圓錐齒輪副的設計計算方法、齒廓生成方法及加工制造方法的正確性。

3 結論

本文基于齒輪空間嚙合原理，分析了范成法生成高階橢圓錐齒輪齒廓時，范成刀具的空間走刀位置，推導出了高階橢圓錐齒輪的齒面方程；結合三維軟件的二次開發，得到了高階橢圓錐齒輪實體模型及虛擬裝配體；建立了五軸聯動數控銑床的坐標系，分別加工出了二階、三階、四階橢圓錐齒輪，并通過對滾檢查試驗及嚙合傳動試驗，驗證了范成法生成高階橢圓錐齒輪齒廓模型的正確性，以及五軸聯動數控加工高階橢圓錐齒輪制造方法的可行性。

[1] 譚偉明，梁燕飛，安軍，等．漸開線非圓齒輪的齒廓曲線數學模型[J]．機械工程學報，2002，38(5)：75-79.

[2] 趙玉民，馬延會，華林，等．非圓錐齒輪節曲線的平面展開算法研究[J]．中國機械工程，2008，19(17)：2046-2049.

[3] Xia Jiqiang, Liu Yuanyuan, Geng Chunming, et al. Noncircular Bevel Gear Transmission with Intersecting Axes[J]. Journal of Mechanical Design, Transactions of the ASME, 2008, 130(5): 1-6.

[4] 姜虹，王小椿．三周節變傳動比限滑差速器設計與試驗[J]．農業機械學報，2007，38(4)：31-34.

[5] 劉繼勝, 羅姜．非圓齒輪的滾齒加工數控技術研究[J]. 機床與液壓,2009,37(9): 62-65.

[6] 吳序堂，王海貴．非圓齒輪及非勻速比傳動[M]．北京：機械工業出版社，1997.

[7] 夏繼強,耿春明,宋江濱,等.變傳動比相交軸直齒錐齒輪副幾何設計方法：中國，200410009582.6[P]. 2006-03-29.