城際公交車高峰時段發車間隔時間優化

曲思源 徐行方 洪 玲

（同濟大學交通運輸工程學院1） 上海 201804） （上海鐵路局調度所2） 上海 200071）

公交車輛發車時刻表是公共交通管理系統中重要的計劃表，是調度員工作以及車輛正常運行的最基本依據．編制車輛發車時刻表最關鍵的問題就是確定發車間隔．伴隨著我國城際鐵路的發展，“大運量、小編組、高密度、公交化”的運營模式營模式使得城際鐵路在城際客運通道中客流分擔率逐漸上升．為確保城際公交車客流分擔率保持平穩或上升，同時滿足旅客出行需要，城際公交車發車間隔應當按照“以人為本”的原則，以較高的行車密度、較少的旅客候車時間，實現旅客方便、便捷、快速地出行，即旅客在一定的時間范圍內，幾乎不受車輛到發時刻限制，可隨到隨走，并以較短的旅行時間到達目的地．一般說來，城際公交車發車間隔要根據不同時間內乘客需求的變化來制定不同時段的發車間隔時間，可將時段劃分為早高峰、平峰和晚高峰3個不同時段，特別是高峰時段，其開行車次的間隔時間優化是衡量城際公交運營質量重要的參數．在研究發車間隔方面，已有文獻多是在發車間隔均等的前提下展開研究的，如文獻［1］將車輛出行費用描述為計劃延誤費用和車內費用兩部分，以旅客出行費用和鐵路成本費用最小化為目標建立了優化模型并進行了分析求解．文獻［2］建立了理想狀態下的城際軌道交通旅客候車時間總和數學期望最小的多目標規劃模型．本文將旅客到達城際公交站發站的過程視為隨機過程，模擬旅客提前到站候車時，根據公交車不同停站類型有多輛車選擇乘坐的實際，建立起不均等的公交車開行間隔時間優化模型和相應旅客候車等待時間的數學模型，以便為城際公交運營組織的優化提供借鑒．

1 泊松過程

定義1 若｛N（t），t∈［0，＋∞）］為一計數過程，當滿足如下條件：N（0）＝0；對于任意的s≥t≥0，Δt＞0，增量N（s＋Δt）－N（t＋Δt）與 N（s）－N（t）具有相同的分布函數；對于任意的正整數n，任意的非負實數0≤t0≤t1≤…≤tn，增量N（t1）－N（t0），N （t2）－N （t1），…，N （tn）－N（tn－1）相互獨立；對于足夠小的 Δt，有

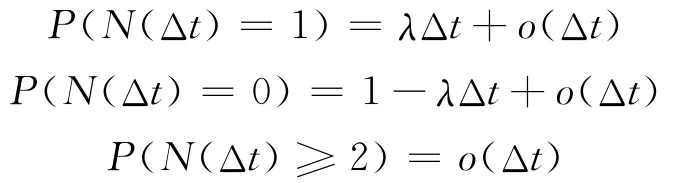
則稱｛N（t），t∈［0，＋∞）］是強度為λ的泊松過程，其數學期望

引理1 設｛N（t），t≥0｝是一泊松過程，N（t）表示［0，t）內質點出現的個數，以τn表示第n 個質點的到達時刻，n＝1，2，…，其累計分布函數和概率密度分別為［3］

引理2 設｛N（t），t≥0｝在［0，t）時段內進入含有n個子系統L的隨機質點個數，每個質點獨立地以概率Pj，（j＝1，2，…，m； ＝1）進入L的第j個子系統，用Nj（t）表示在［0，t）時段內進入第j個子系統的隨機質點個數，若N（t）服從強度為λ的泊松過程，則N（t）＝ （t），｛Nj（t）相 互 獨 立；j ＝ 1，2，…，m｝，且 固 定t，｛Nj（t）｝是強度為λPj的泊松過程．

引理3 設｛N（t），t≥0｝是強度為λ的泊松過程，對于任意的實數t＞0，若N（t）＝n＞0，則該過程的前n個質點發生的時刻（τ1，τ2，…，τn）和n個在［0，t］上均勻分布的相互獨立的隨機變量（U1，U2，…，Un）的次序統計量有相同的n維聯合分布［4］．

2 模型建立

2．1 公交車開行間隔時間模型

根據大量的數據調查可知，有60%的旅客愿意提前30～60 min到達始發站．定義旅客候車時間是指旅客到公交始發站候車時起至乘坐某一輛車次出發時止的整個過程．某同一方向，旅客一般按照車次時刻表提前到站候車，且有不同停站方案的多輛車次可供選擇．針對旅客候車的實際，模擬同一去向的旅客在［0，t］內陸續到達始發站，該始發站安排Aj（1≤j≤m）輛供旅客選擇，設到達該始發站的旅客數N（t）是一服從強度λ的泊松過程，每個旅客進入Aj輛車的概率分別為pj（j＝1，2，…，m ＝1），用 Nj（t）表示在［0，t）時段內進入第Aj輛的隨機旅客數，根據引理2可知N（t）＝ （t），｛Nj（t）相互獨立；j＝1，2，…，m｝，并且｛Nj（t）｝是強度為λPj的泊松過程．以τn，j表示Aj輛車第n個旅客的到達時刻，n＝1，2，…，則累計分布函數和概率密度分別為

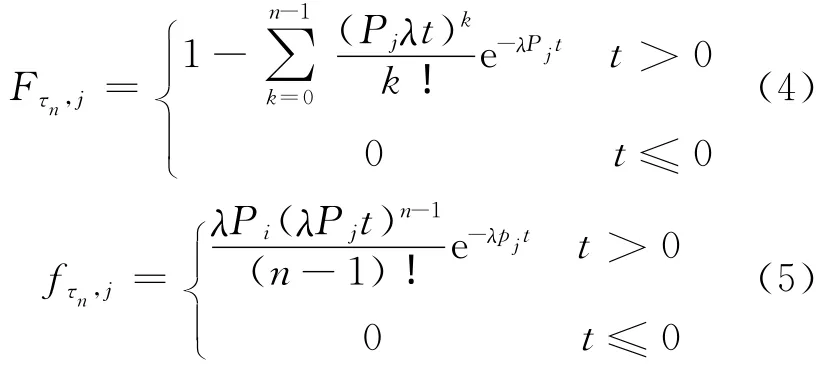
假設當旅客到達數為n時，該輛便發車，即第n位旅客到達的數學期望為該次車輛等待時間的數學期望

令Aj輛發車的時間為tj，有

則合理的車輛間隔為

根據分布函數的定義，有Fτn，j（t）＝P（τn，j≤t），注意到｛τn，j≤t｝表示第n個旅客在時刻t之前出現，這就意味著在［0，t）內至少到達了n個旅客，于是有

若令n表示定員時，理論上可用Fτn，j表示Aj輛的上座率，根據式（4）、（7）可分別求得每輛的上座率ρj．

2．2 旅客等候時間模型

設［0，t）時段內進入 Aj輛車旅客數Nj（t），設第i個旅客到達車站的時刻為Wji，則在［o，t］到達車站的旅客等待Aj時間總和為［5－7］

因為

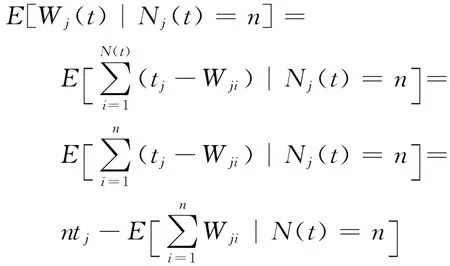
記｛Yi，1≤i≤n｝為［0，t］上獨立同均勻分布的隨機變量，Y（1）≤Y（2）≤…≤Y（3）為相應的順序統計量．由引理3，存在

因此

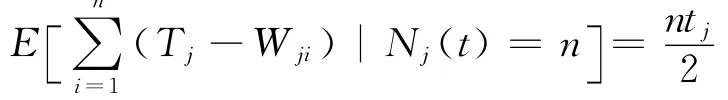
所以

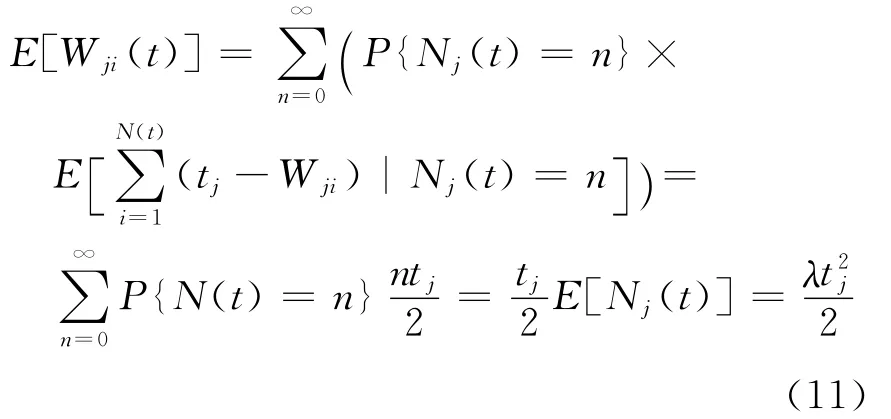
3 算例分析

某一城際公交站早高峰時段內，允許最小開行間隔時間為5 min，采用同一型號車，每車定員為50人，在某一高峰時段內，擬安排4種類型，以沿線所設站為衡量標準，即一站直達A、跨線運行（三站起停）B、快車（二站起停）C和慢車（站站停）D四種類型，同一去向的旅客到達車站服從泊松過程，其到達強度λ＝50人／min，準備安排9輛車該時段始發，始發順序為1～9（車次代號），通過客流調查，旅客進入每輛車的概率分別為

求合理的始發間隔時間和旅客候車等待每次輛車的平均等待時間總和．

根據式（1）、（8）、（11），可計算各車次間隔時間計算表，見表1．

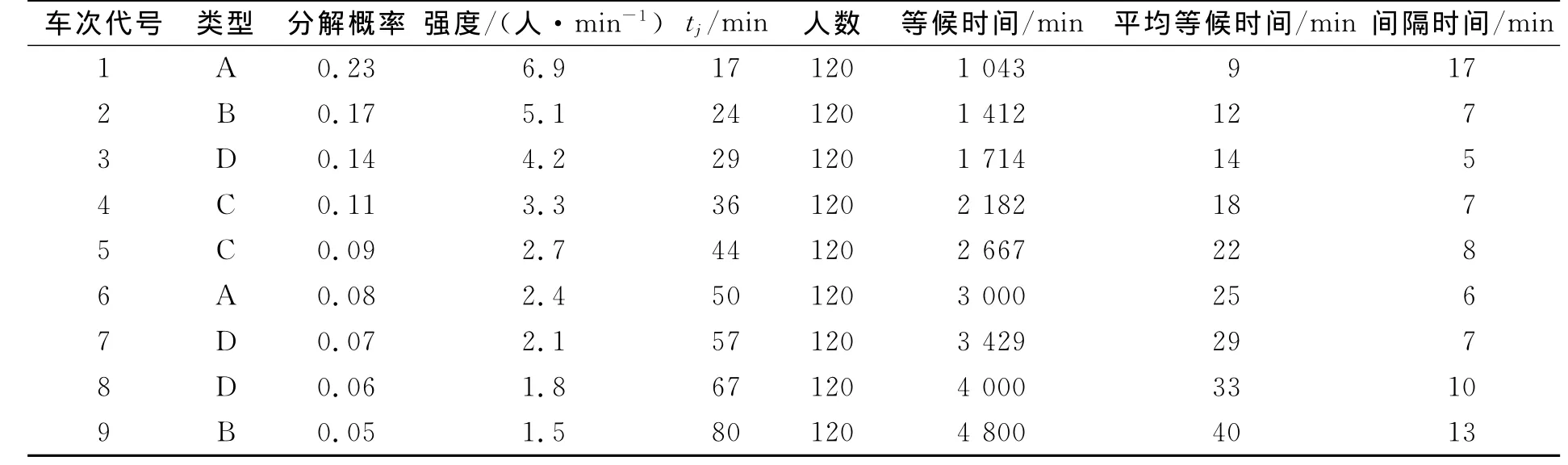
表1 各車次間隔時間計算表

顯見，在［0，80］的時間時段內，可分別求得各車輛在該始發站發車不均等的間隔時間，其中第4輛和第3輛采取追蹤運行模式，即兩輛車間隔時間僅為5 min，該模型能為采取公交車輛追蹤開行方式的原因提供理論依據．同時，也能驗證，若分解概率越低，各車次發車間隔時間將越長．

4 結束語

城際公交始發站發車間隔時間是基于公交化運營模式，據旅客到達強度，采用隨理論求得的不確定模型．考慮到每一時段旅客到達車站強度分配各次輛車的強度值是模型優化的必要條件，因此需要深入進行客流調查，以便取得準確的數值．輛車開行不均等間隔時間模型同時能為輛車開行方案的優化提供了新的思路．城際公交車發車間隔除根據乘客需求、車型定員、滿載率外，還要依據行駛速度、停站安排和時間、線路通行能力、交通流量等因素綜合確定，其車輛間隔時間優化有待進一步分析．

［1］秦 進，史 峰．公交化城際輛車的最優時刻表研究［EB／OL］．［2011－10－11］中國科技論文在線．http：／／www．paper．edu．cn．

［2］廖 勇．公交化城際列車開行間隔優化［J］．鐵道學報，2010，32（1）：8－12．

［3］李裕奇．隨機過程［M］．北京：國防工業出版社，2003．

［4］王志剛．應用隨機過程［M］．合肥：中國科學技術大學出版社，2009．

［5］肖龍文，史 峰．鐵路公交化旅客列車開行方案優化［J］．湖南大學學報：自然科學版，2009（1）：55－58．

［6］謝如鶴，宗 巖，王榮華，等．城際鐵路客運公交化的綜合評價［J］．廣州大學學報：自然科學版，2005（1）：78－82．

［7］許煥衛，黃洪鐘，張 旭．基于模糊折中規劃的穩健多目標優化設計［J］．大連理工大學學報，2007（3）：56－60．