基于不確定性準則的薄壁管耐撞可靠性設計

張 勇 徐西鵬 楊永柏 張 成

華僑大學，廈門，361021

0 引言

薄壁結構的耐撞性是現代汽車安全性設計研究的熱點。碰撞事故發生時，薄壁構件受到劇烈沖擊產生塑性變形，吸收大量的碰撞能量，從而提高車內乘員的安全指數［1-2］。薄壁管的變形吸能模式對車體碰撞時的加速度與碰撞力具有重要影響，與車內乘員的安全性息息相關。但是，傳統薄壁結構的耐撞性設計仍局限于確定性優化設計的研究，忽略了產品設計、制造過程中的諸多不確定因素，如幾何尺寸、材料屬性、載荷和邊界條件等［3-5］。同時，車身的運行工況常具有一定的不確定性，這些不確定因素將導致設計區間的波動，使得設計響應超出設計約束，導致設計在全生命周期管理過程中的可靠性大大降低。

同時，影響薄壁圓管耐撞性能的因素也較多，一些研究人員已針對薄壁圓管的截面半徑及厚度開展了確定性耐撞性設計。但是，薄壁圓管的長度對其耐撞性也有重要影響，長度過大，碰撞過程中易出現彎曲變形而喪失吸能性，長度過小則碰撞吸能性大大降低。因此，本文以薄壁圓形件的厚度、半徑及長度為設計變量，更加全面地評價其在多種影響因素下的耐撞性。國內外關于薄壁構件抗撞性的研究仍主要集中于薄壁構件的實驗與仿真對比、薄壁構件的截面形狀的敏感性確定性［6-10］，而對薄壁構件在不確定性因素下的可靠性卻研究較少。因此，筆者以顯示有限元技術為基礎，將響應面近似技術與可靠性優化方法相結合，將可靠性評價準則應用于薄壁圓管的耐撞性優化設計。優化結果不僅較好地達到了對薄壁管吸能性的目的，而且使其具有較高的使用可靠性。

1 響應面近似模型方法

響應面方法是處理多變量問題建模與分析的一套統計方法［11］。它主要通過對設計空間的數據采樣，探測設計變量與設計響應之間的敏感度，擬合設計變量和設計響應之間的函數關系，從而把工程優化問題轉變為數值優化設計問題，以此提高優化設計效率。

響應面模型表征了一組獨立設計變量與設計響應之間的近似函數關系［12-13］:

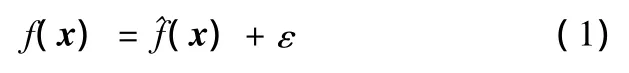
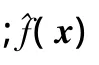
其中，xi為設計變量;M為設計變量的個數;β0、βi、βii、βij為多項式的待定系數，采用最小二乘方法可確定多項式系數的具體數值［12-13］。

試驗設計是探測設計空間的主要方法之一，它直接影響到設計空間樣本點選取的均勻性與合理性，以及后續響應面近似模型的精度。因此，文中采用最優拉丁方試驗設計方法并編寫了其采樣程序［11］。相比傳統的拉丁方實驗設計，它能更能均勻地分布設計采樣點，從而最大程度地獲取了設計空間的設計信息。

2 可靠性優化設計方法

確定性優化設計過程中，材料參數、幾何參數的不確定性常被忽略，使得確定性最優解只存在于一個狹窄的設計空間，導致確定性優化解的可靠度降低。此外，傳統的安全系數可靠性評價方法常具有一定的經驗性。因此，概率可靠性優化設計理論在工程結構的設計中得到了廣泛的應用，可靠性優化設計問題的數學模型為［15］

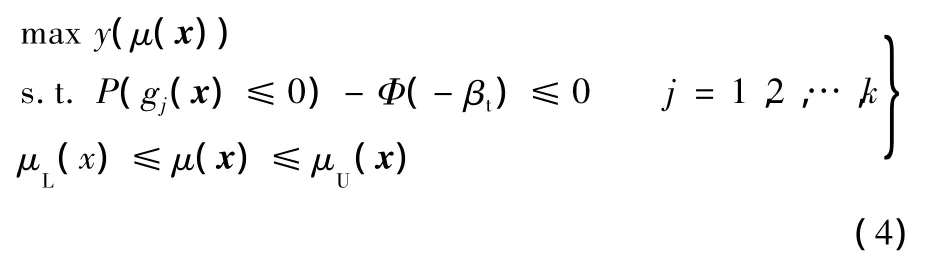
式中，y(μ(x))、gj(x)分別為目標函數與約束函數;μ(x)為隨機設計變量x的均值;k為概率約束的數目;Φ(·)為標準正態分布函數的累積分布函數;βt為期望的可靠度目標。

失效概率分布函數P(gj(x)≤0)能定義累積分布函數Fgj(0)，即為

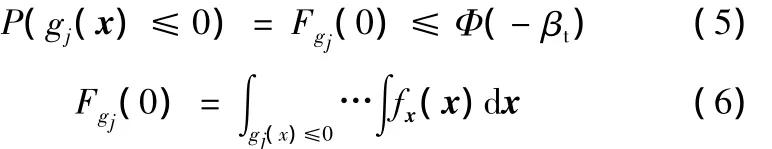
式中，fx(x)為隨機變量的聯合概率密度分布函數。

由式(6)可知，可靠性分析過程需要求解一系列的多重積分，因此，難于獲取可靠性分析的解析解，因此，文中采用一階可靠性分析方法來近似求解式(6)。

綜上可知，可靠性優化是一個雙循環優化迭代過程，外循環為優化過程，內循環為可靠性分析過程。由于可靠性分析處于內循環中，如果直接基于有限元模型來進行可靠性分析，那么，為了求解概率約束，每次優化過程都需要多次進行有限元計算，導致可靠性優化過程耗費大量的計算成本，從而陷入由計算復雜性引起的優化設計瓶頸。因此，基于多項式響應面近似技術與概率可靠性理論，文中提出一種新穎的薄壁管耐撞性優化設計方法，加快可靠性分析速度，降低耐撞性分析問題的計算復雜度。圖1為可靠性優化設計的簡單示意圖。

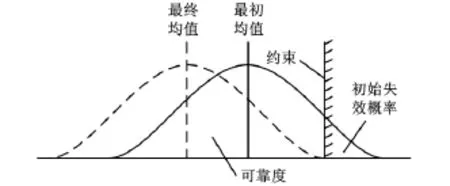
圖1 可靠性優化示意圖

3 薄壁管耐撞性與可靠性設計

3.1 薄壁管耐撞確定性優化模型的建立

碰撞事故發生時，車輛的一部分結構件主要用于承擔各種不規則載荷的作用，以保持整個車體的結構完整性。此外，作為車體另一重要組成部分的薄壁圓管在汽車碰撞過程中發生折疊變形而吸能，從而有效控制車體的碰撞減速度，提高車輛的安全性。因此，文中以薄壁圓管的最大吸能量與碰撞力為耐撞性設計指標，建立了薄壁圓管的耐撞性有限元優化模型。整個模型由4409個節點與4184個單元構成，其截面形狀及設計參數(圓管直徑R與長度L)如圖2所示。

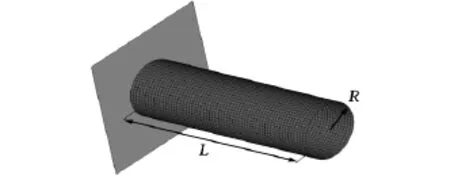
圖2 薄壁圓管耐撞性模型

優化設計過程中，圖2所示的薄壁圓管以13.8m/s的速度撞擊剛性墻，整個有限元碰撞仿真過程是在非線性有限元軟件LS－DYNA中進行的。優化設計以圓管半徑R(mm)、圓管厚度T(mm)、薄壁圓管的長度L(mm)為設計變量。考慮車體安全性設計為主要目標，故以薄壁圓管的吸能量E(J)為設計目標，為了減小碰撞過程中的加速度，以薄壁圓管的最大碰撞力Fmax(kN)為設計約束。此外，由于不可再生能源的日益枯竭，研究數據顯示，若汽車整車質量減小10%，燃油效率可提高6% ～8%，油耗將減少10%，排放量降低5% ～6%［16］，汽車輕量化設計也是當前車體設計主要考慮的因素之一。因此，本文也把薄壁吸能圓管的質量m(kg)作為設計約束，從而使薄壁圓管的設計滿足輕量化設計的要求。最后，薄壁圓管的耐撞性確定性優化問題的數學模型可以表示為

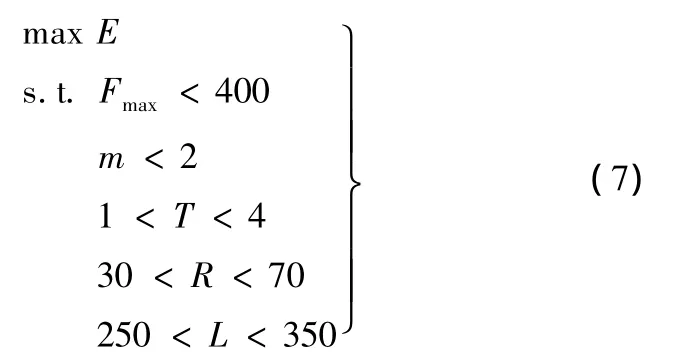
3.2 薄壁圓管耐撞性確定性優化過程

薄壁圓管的碰撞過程是一個高度非線性的動態過程，導致整個碰撞分析過程非常復雜。此外，由于整個優化過程與后續的可靠性分析過程相關，如果基于有限元模型直接進行優化設計，它調用正問題(薄壁管有限元分析)的次數將非常巨大，導致優化過程具有高昂的計算成本。因此，構建薄壁圓管耐撞性優化研究的設計約束、設計目標與設計變量之間的響應面近似模型成為解決該問題的關鍵。

本文結合試驗設計、近似模型與小種群遺傳算法對薄壁圓管的確定性優化問題進行尋優。優化設計流程如圖3所示。

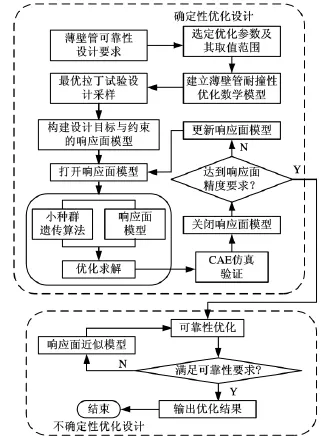
圖3 薄壁管耐撞性與可靠性優化流程圖

確定性優化中，初始設計變量R=50mm，L=300mm，T=2mm，Fmax=547kN，m=1.46kg，都不滿足式(7)的設計約束條件，因而需要進行優化計算。采用最優均勻拉丁方實驗設計技術，通過20個采樣點構建了薄壁圓管吸能量、最大碰撞力及薄壁圓管質量的二次響應面近似模型，并在優化過程不斷增加試驗設計點來更新近似模型，直到達到優化的收斂準則為止。設計變量的取值、目標和約束的初始值與最優值如表1所示。

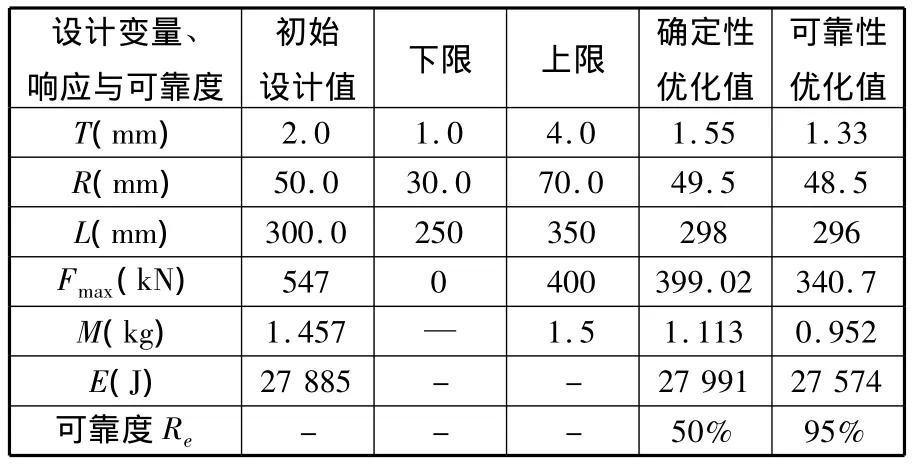
表1 設計變量和響應的初始值和優化值

由表1分析可知，確定性優化過程中，由于強加了薄壁吸能圓管的質量與最大碰撞力為設計約束，導致圓管的吸能量增加不明顯，但是，優化結果卻使薄壁管的最大碰撞力和質量都有了較大幅度的減小，其中最大碰撞力降低幅度達到27%，質量也減輕了約23%。但是，在確定性優化設計中，最大碰撞力的確定性最優值與設計上限之間已相當接近，如果薄壁圓管的設計變量值因不確定性因素的影響產生波動，那么確定性優化得到的最大碰撞力極有可能超出約束上限，導致確定性優化結果失效。由此可知，確定性最優解不是可靠性最優解。然而，在工程實際中，我們最關心的卻是可靠性最優解。因此，針對薄壁管的耐撞性優化設計，還需要在確定性優化設計的基礎上開展可靠性分析與優化。

3.3 薄壁圓管可靠性優化設計

針對薄壁圓管的可靠性優化問題實質上是一個不確定性優化設計的問題，文中運用概率不確定性建模方法。薄壁圓管可靠性優化的數值模型為

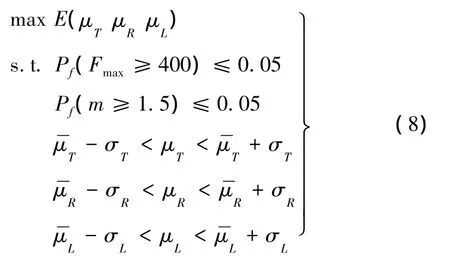
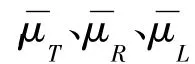
由表1可知，確定性優化結果使得薄壁圓管的最大碰撞力處于臨界狀態，且由可靠性分析可知，確定性優化結果僅有50%的可靠度，這完全不滿足產品的使用可靠性要求，而經過式(8)的可靠性優化設計后，最大碰撞力的可靠性最優值遠離設計約束上限，并具有95%的可靠度，較好滿足了可靠性設計要求，最大碰撞力較初始設計減小了約38%，較確定性最優點也降低了約15%，另外，薄壁圓管的質量約束較初始設計減小了約35%，較確定性最優點也降低了約14%，但是，可靠性最優吸能值E(J)相對于初始設計而言，犧牲了約1%的吸能量，對其碰撞吸能性幾乎沒有影響，由此可知，可靠性優化設計不僅較好地達到提高薄壁圓管耐撞性的目的，而且使薄壁圓管的使用可靠性得到了大幅度的提高，符合車輛安全性、輕量化與可靠性設計要求。圖4顯示了初始設計與可靠性優化設計后圓管的最大碰撞力曲線。

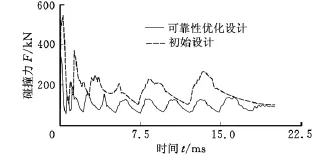
圖4 初始設計與可靠性優化設計碰撞力曲線對比圖

4 結語

本文將試驗設計、響應面近似模型與基于概率的可靠性評價方法相結合，構建了基于薄壁圓管質量工程的優化設計方法。在薄壁圓管設計之初就考慮了它的使用可靠性要求，避免了安全系數法設計余量過大的缺陷。同時，在確定性與不確定性優化過程中引入了響應面方法，用多項式數學模型替代薄壁圓管的物理有限元模型，提高了整個優化過程的計算效率。優化結果相對于初始設計而言，不僅較大幅度地提高了薄壁圓管的可靠度，而且使得它的設計更加安全與輕量化。研究結果表明:本文提出的可靠性優化設計方法具有較高的精度和較強的工程實用性。同時，可將該方法推廣應用到汽車其他薄壁構件及其整車的耐撞性分析中，為整車其他零部件的安全性設計提供一種新的解決方案。

［1］鐘志華，張維剛，曹立波，等.汽車碰撞安全技術［M］.北京:機械工業出版社，2003.

［2］McNay G H.Numerical Modeling of Tube Crush with Experimental Comparison［C］//SAE Passenger Car Meeting and Exposition，1988:880898.

［3］Choi K K，Youn B D，Yang R J.Moving Least Square Method for Reliability－based Design Optimization［C］//Proceedings of 4th World Congress of Structural and Multidisciplinary Optimization.Dalian，2001:1-6.

［4］Youn B D，Choi K K.A New Response Surface Methodology for Reliability Based Design Optimization［J］.Computers and Structures，2004，82(2/3):241-256.

［5］張義民，賀向東，劉巧伶，等。汽車零部件的可靠性穩健優化設計—理論部分［J］.中國工程科學，2004，6(3):75-79.

［6］Song H W，Fan Z J，Yu G，et al.Partition Energy Absorption of Axially Crushed Aluminum Foam－filled Hat Sections［J］.International Journal of Solids and Structures，2005，42(9/10):2575-2600.

［7］Chiandussi G，Avalle M.Maximization of the Crushing Performance of a Tubular Device by Shape Optimization［J］.Computers ＆ Structures，2002，80(27/30):2425-2432.

［8］White M D，Jones N.Experimental Quasi－static Axial Crushing of Top－hat and Double－hat Thin－walled Sections［J］.International Journal of Mechanical Sciences，1999，41(2):179-208.

［9］Abedrabbo N，Mayer R，Thompson A，et al.Crash Response of Advanced High－strength Steel Tubes Experiment and Model［J］.International Journal of Impact Engineering，2009，36(8):1044-1057.

［10］Zarei H R，Kroger M.Multi－ objective Crashworthiness Optimization of Circular Aluminum Tubes［J］.Thin － walled Structures，2006，44(3):301-308.

［11］張勇，李光耀.基于可靠性的多學科設計優化在薄壁梁輕量化設計中的應用研究［J］.中國機械工程，2009，20(15):1885-1889.

［12］Myers R H，Mongomery D C.Response Surface:Process and Product Optimization Using Designed Experiments［M］.New York:Wiley Publishers，1995.

［13］王海亮，林忠欽，金先龍.基于響應面模型的薄壁構件抗撞性優化設計［J］.應用力學學報，2003，20(3):61-66.

［14］張立新，隋允康，高學仕.基于響應面方法的結構碰撞優化［J］.力學與實踐，2005，27(3):35-39.

［15］Gu L，Yang R J.Recent Applications on Reliability －based Optimization of Automotive Structures［C］//SAE 2003 World Congress ＆ Exhibition.Detroit，MI，USA，2003:2003-01-0152.

［16］燕占秋，華潤蘭.論汽車輕量化［J］.汽車工程，1994，16(6):375-383.