基于多粒度語言的動態聯盟合作伙伴群決策

彭安華 肖興明

1.中國礦業大學，徐州，221116 2.淮海工學院，連云港，222005

0 引言

虛擬企業是一種嶄新的企業組織形式，是21世紀企業進行生產經營活動和參與市場競爭的主要模式。面對某一市場機遇時，最先抓住機遇并掌握一定核心能力的企業首先要對自身核心資源進行分析，判斷實現市場機遇所需的核心資源與自身資源是否匹配。如果兩者匹配，則核心企業通過自身努力來抓住市場機遇，反之，核心企業則根據具體情況通過組建虛擬企業或者并購外部資源來抓住市場機遇。如果選擇組建虛擬企業，則該核心企業稱為盟主。對盟主而言，在確定新產品開發目標后，首先進行項目分解，將總項目分解成若干個可由單獨企業承擔的子項目，為每個子項目設計招標書，然后通過公共信息網絡進行招標。在同一時間內有眾多的企業投標，如何從這些投標企業中選擇最佳的合作伙伴，是組建虛擬企業過程中最為關鍵的一步。文獻［1］提出了基于層次分析法的合作伙伴選擇方法，文獻［2］提出了基于層次分析法和數據包絡分析的合作伙伴選擇方法，文獻［3］提出了基于改進型灰色評價的虛擬企業合作伙伴選擇方法。這些文獻中的判斷矩陣或效用值及其評價指標的權重都是用一個精確數表示的。

然而在實際決策中，由于客觀事物的復雜性及人類認識的局限性，往往很難確定一個精確數，即使給定一個精確數，也是比較主觀的，不一定能反映實際情況。文獻［4－5］提出基于模糊層次分析法的合作伙伴選擇方法，首先給出語言判斷矩陣，然后給出語言偏好信息的隸屬函數，例如“高”、“很高”等語言的隸屬函數分別用三角模糊數［0.7，0.9，1.0］和［0.9，1.0，1.0］表示，而事實上隸屬函數在實踐中并不是總能獲得，因而該方法在實際應用中仍存在一定的困難。文獻［6］提出的基于證據推理的合作伙伴選擇方法，雖不需要將語言評價轉為精確數或模糊數，但需要事先給每個語言評價的確定置信度，這顯然也比較主觀。由Herrera等［7］提出的二元語義可直接對語言評價信息進行計算，但目前還沒見到基于二元語義信息的合作伙伴選擇方法。文獻［8］提出了一種基于二元語義信息處理的群體決策方法，該文中有兩個問題值得商榷：①由于對屬性的認識程度不同，故不同的決策者可能依據不同粒度語言評價集給出語言評價值；②屬性的權重一般很難精確得到，尤其當決策問題比較復雜時。虛擬企業合作伙伴選擇過程中，由于涉及因素多，且有很多抽象因素無法用數值精確描述，故用諸如“好”、“較好”來描述，更符合人們的思維習慣。本文提出一種在部分權重的情況下基于多粒度語言評價值的動態聯盟中的合作伙伴選擇方法。

1 不同粒度語言評價值的一致化

關于二元語義的基本概念可參考文獻［9－10］。

定義1 設β∈［0，T］為語言評價集S經某種集結方式得到的一個實數值，則β可由函數Δ表示為二元語義：

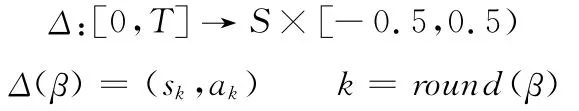
式中，sk為語言評價集S中第k＋1個語言評價值；ak為sk的符號平移，ak＝β－k；round（＊）為四舍五入取整算子。

定義2 設（sk，ak）是一個二元語義，則存在一個逆函數Δ－1，使其轉換成相應的數值β∈［0，T］：

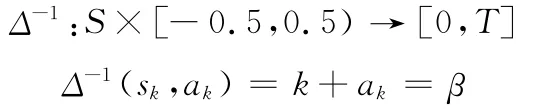
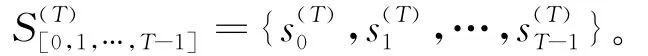
基于多粒度語言評價信息的群決策問題首先將不同語言評價集一致化為標準語言評價集。文獻［11］基于模糊理論中的擴展原理，采用最大最小隸屬度原則，將不同粒度語言評價信息轉化為定義在基本語言評價集上的模糊數。文獻［12］通過插值方法將不同粒度語言評價信息一致化為基本語言評價信息。文獻［11-12］使用三角模糊數來表達語言評價集中短語所對應的語義，計算過程比較繁瑣，而且只能從粒度低的評語集向粒度高的評語集轉化。

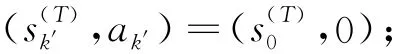
2 二元語義集結算子

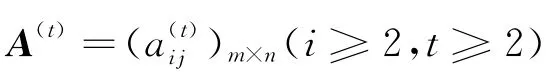
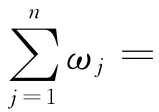
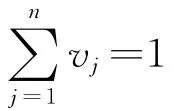
其中，π（j）（j＝1，2，…，n）是1，2，…，n中的一個置換。對任意j＝2，3，…，n 有（sπ（j－1），aπ（j－1））≥（sπ（j），aπ（j））。

ET－OWGA算子只考慮了數據位置的重要程度，即只根據某個數據在整個數據列當中的相對大小賦予不同的權重，而沒有考慮數據自身的重要程度，即在多屬性決策中沒有考慮不同的屬性具有不同的權重。參考文獻［14］，本文提出擴展的組合加權幾何平均算子（ET－COWGA）。

定義6 設｛（s1，a1），（s2，a2），…，（sn，an）｝為一組二元語義信息，由于每個數據自身的重要程度不同，且設數據自身的權重向量為ω，位置權重向量v是與擴展的二元語義有序組合加權幾何平均（ET－C OWGA）算子φ相關聯的加權向量，則φ定義為

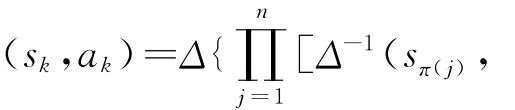
應用OWG算子的關鍵是確定位置權向量v，確定位置權向量的方法主要有模糊量化方法、最大熵規劃模型、最小方差規劃模型、極大極小離差規劃模型［15］，但這些方法要么是物理含義不夠清楚，要么是計算過程比較復雜。在數據列當中，出現在平均值附近的數據比較合理，應該賦予較大的位置權重，遠離平均值的數據則說明該數據不盡合理，應該賦予較小的權重，以弱化不合理數據對數據集結結果的影響。基于此，筆者提出基于正態分布的方法來確定OWG算子中的位置權向量：

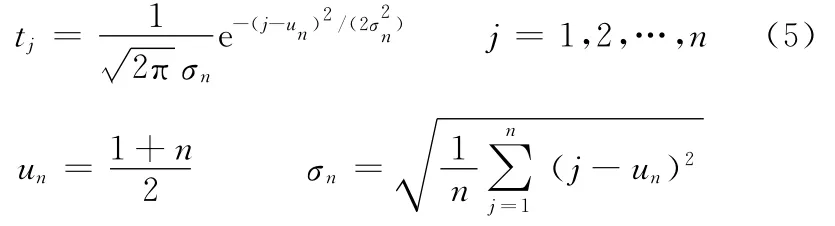
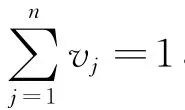
3 基于兩階段優化確定屬性權重向量

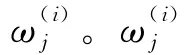
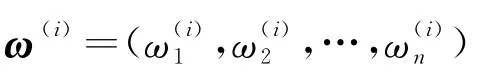
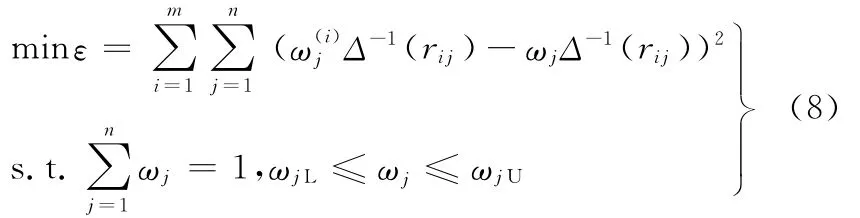
利用MATLAB軟件中的fmincon函數求解此模型，將得到最終精確權重向量ω。

4 虛擬企業合作伙伴決策

虛擬企業合作伙伴選擇的框架主要分為4個階段（圖1）［16-17］：第一個階段為市場機遇實現模式的選擇，即通過分析確定是采用并購模式還是組建虛擬企業或者放棄市場機遇。第二階段為評價指標的確定，評價指標的確定主要是在參考虛擬企業指標庫的基礎上，根據任務分解確定評價指標［18］。第三階段為篩選，確定必須要滿足要求的硬指標，若任何一項硬指標不滿足要求，則淘汰該方案。第四階段為合作伙伴綜合評價，即在滿足硬指標要求的有限個合作伙伴中選擇最佳的合作伙伴。一個產品的制造過程大體上可分為產品設計、零部件制造、總裝、銷售等4個業務過程，如果盟主主要具有產品設計能力，則盟主要為其他3個業務過程尋找最理想的合作伙伴。現假設盟主為產品的銷售尋找普通型的緊密型合作伙伴。評價指標確定為企業績效u1、企業先進程度u2、企業產品質量u3、企業環境u4，相應的權重分別為ω～1＝ ［0.3，0.5］，ω～2＝ ［0.2，0.3］，ω～3＝ ［0.1，0.2］，ω～4＝［0.15，0.35］，現假設請了3個專家d1、d2、d3進行評判，經過篩選后有3家合作伙伴x1、x2、x3，要經過綜合評價才能確定誰是最佳合作伙伴。假設3個專家給出的語言評價值如表1所示。一般地講，若專家對某種評價指標或者對某一候選企業比較熟悉，則給出的較大粒度的語言評價值，反之則給出較小粒度的語言評價值，圖1描述了其詳細的決策過程。

表1 評價指標及各專家語言評價值

4.1 語言評價值一致化

假設以7粒度語言評價集為標準語言評價集，按照定義3（式（1））將3粒度語言和5粒度語言都統一轉換為7粒度語言評價集中的語言評價：

4.2 集結專家語言評價值

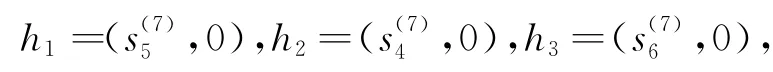
4.3 求出精確權重向量

4.3.1 求出局部優化權重向量

例如以合作伙伴x1的綜合屬性值為最優，根據式（7）建立如下最優化模型

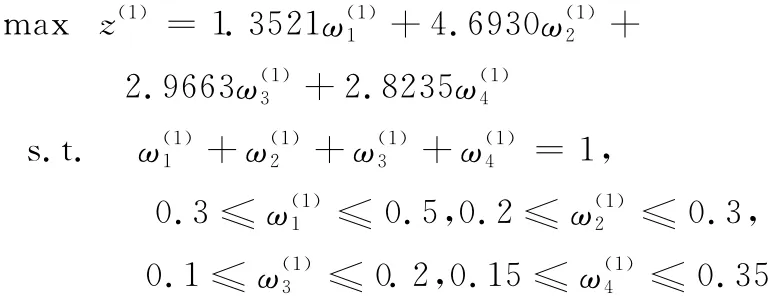
4.3.2 求出精確權重向量

根據式（8）建立如下最優化模型

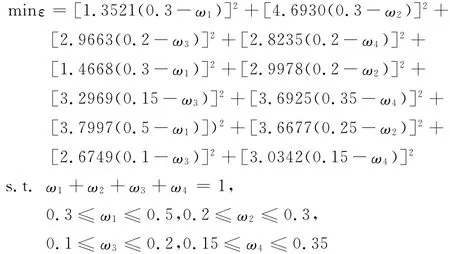
利用MATLAB軟件中的fmincon函數求解此模型，可得到精確權重向量ω＝（0.4101，0.2453，0.1210，0.2235）。

4.4 求合作伙伴綜合評價值

利用定義4（式（2））計算出x1的綜合評價值值。

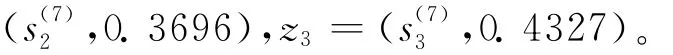
5 結論

（1）在專家語言評價值集成的過程中采用ET－COWGA算子，既考慮了數據自身的重要性，又考慮了數據位置的重要性，減小了過高或過低評價的不合理影響，提高了評價結果的準確性。

（2）采用基于正態分布的辦法求位置權重向量，該方法相對于目前常用的方法具有物理含義明確、易于理解、計算簡單等優點。

（3）直接利用語言評價，無需給出偏好信息的隸屬函數，方便了專家評價。根據評價矩陣采用二階段優化的辦法求出精確的屬性權重。模糊性與精確性結合，進一步提高了評判結果的準確性。

（4）為了提高評價數據的準確性，可構造層次結構的評價指標體系，例如可將企業績效細分為企業發展前景、企業信譽水平、產品市場占有率及新產品開發成功率等，這時就構成了一個多層次的模糊多屬性決策問題，求解方法與本文類似，只是在每一層次重復利用本文的方法。

［1］鄭文軍，張旭梅，劉飛，等.虛擬企業合作伙伴評價體系及優化決策［J］.計算機集成制造系統－CIMS，2000，6（5）：63－67.

［2］盧級華，李艷.基于DEA／AHP的虛擬企業合作伙伴選擇 ［J］.東 北 大 學 學 報，2008，29（11）：1661－1664.

［3］張成考，聶茂林，吳價寶.基于改進型灰色評價的虛擬企業合作伙伴選擇［J］.系統工程理論與實踐，2007，27（11）：54－60.

［4］馬永軍.網絡聯盟企業中設計伙伴選擇方法［J］.機械工程學報，2000，36（1）：15－19.

［5］李帥.基于模糊群決策的虛擬企業合作伙伴選擇［J］.東北大學學報（自然科學版），2004，25（3）：295－298.

［6］廖貅武，唐煥文.動態聯盟中伙伴選擇的證據推理方法［J］.計算機集成制造系統－CIMS，2003，9（1）：57－61.

［7］Herrera F，Martinez L.A 2－tuple Fuzzy Linguistic Representation Model for Computing with Words［J］.IEEE Transactions on Fuzzy Systems，2000，8（12）：746－752.

［8］鮑廣宇，付豐科，趙志敏.一種基于二元語義信息處理的群體決策方法［J］.解放軍理工大學學報，2009，10（5）：435－439.

［9］姜艷萍，樊治平.具有語言信息的多指標群體綜合評價［J］.東北大學學報（自然科學版），2005，26（7）：703－706.

［10］張園林，匡興華.一種基于多粒度語言偏好矩陣的多屬性群決策方法［J］.控制與決策，2008，23（11）：1296－1300.

［11］Chen Z F，Berrarieh D.On the Fusion of Multigranularity Linguistic Label Sets in Group Decision Making［J］.Computers ＆Industrial Engineering，2006，51（10）：526－541.

［12］Herrera F，Matinez L.A Model Based on Linguistic 2－tuples for Dealing with Multi－granularity Linguistic Contexts in Multi－expert Decision Making［J］.IEEE Transaction on Systems，Man and Cybernetics，Part B：Cybernetics，2001，31（2）：227－234.

［13］衛貴武，黃登仕，魏宇.基于ET－WG和ETOWG算子的二元語義群決策方法［J］.系統工程學報，2009，24（6）：744－748.

［14］徐澤水，達慶利.一種組合加權幾何平均算子及其應用［J］.東南大學學報，2002，32（3）：506－509.

［15］Xu Z S.An Overview of Methods for Determining OWA Weights［J］.International Journal of Intelligent Systems，2005，20（8）：843－865.

［16］葉飛，孫東川，張紅.面向虛擬企業合作伙伴的新過程框架研究［J］.系統工程理論與實踐，2003（11）：88－94.

［17］陳菊紅，汪應洛，孫林巖.虛擬企業伙伴選擇過程及方法研究［J］.系統工程理論與實踐，2001，21（7）：48－54.

［18］錢碧波，潘曉弘，程耀東.敏捷虛擬企業合作伙伴選擇評價體系研究［J］.中國機械工程，2000，11（4）：397－401.