基于機體翻轉的四足機器人翻越臺階過程的運動學分析

余聯慶 王玉金 王立平 汪紅波 唐焱明

1.武漢紡織大學，武漢，430073 2.清華大學，北京，100084

3.浙江師范大學，金華，321019 4.鄂東職業技術學院，黃岡，438000

0 引言

在自然界和人類社會中，存在人類無法到達的地方和可能危及人類生命的特殊場合，如行星表面、工地、礦井、防災救援的地方等。不規則和不平坦的地形是這些環境的共同特點，這使輪式機器人和履帶式機器人的應用受到限制。由于足式機器人可以利用孤立地面作為支撐，具有較強的地形適應性。在這種背景下，足式機器人的研究便蓬勃發展起來［1］。由于四足機器人具有較好的行走適應性和穩定性，所以國內外開發了多種各具特色的四足機器人［2－4］。

在非結構化環境中，平坦的地面十分有限，并且障礙物的形狀和大小不可預測。障礙物大體可以分為兩大類［5］：一類是體積遠大于機器人系統、機器人系統無法逾越的障礙物，如水池、懸崖等，這時機器人必須繞道行駛或者另外規劃目標路徑；另一類是體積與機器人相當、機器人通過改變自身的構形可以逾越的障礙物，包括坡型、臺階型和溝壑等障礙物。一般說來，機器人通過兩種基本方法改變自身構形［6］：一為“重構”，即模塊的重組；二為“變形”，即本身關節的運動。國外學者做了大量的研究工作，研制了各種各樣的可重構機器人［7－9］。四面體滾動機器人［10］及滾動三角形機器人［11］就是可變形重構的機器人，通過改變伸縮臂長度來實現機器人的變形與移動。但此類機器人的越障速度和能力較低，移動過程不連續，很難在實際中得到運用。

四足機器人傳統的越障方式是：采用三條腿作支撐，另一條腿跨越障礙，直至四條腿均越過障礙。四足機器人前后雙腿均含有髖關節、膝關節和踝關節，具備改變自身構形的能力。本文充分利用四足機器人的關節運動變形能力，提出一種基于機體翻轉的臺階翻越方式。首先對機器人翻轉式翻越臺階周期進行了運動規劃，然后對翻越過程進行了運動學建模與仿真分析，得到機器人各個關節角的變化曲線以及重心的移動軌跡。最后討論了機器人臺階翻越能力與幾何參數之間的關系。為了方便敘述，在下文中將翻越臺階簡稱為越障。

1 四足機器人結構模型

機器人的本體結構直接影響到機器人的性能和技術指標，本文采用類似哺乳動物的四足機器人結構模型，如圖1所示。四條腿采用同樣的結構，每條腿均含有三個主動關節，即髖關節、膝關節和踝關節。大腿與小腿的長度相等，且為機體長度的一半。由于臀關節軸心線和機器人機體平面平行，所以髖關節可以繞軸線旋轉360°。假設足底與地面的摩擦因數足夠大，在越障過程中不會發生足底打滑現象。

2 翻轉式越障運動規劃

四足機器人以翻轉方式越障時，前后雙腿分別執行相同的動作，在運動學分析時可將前后雙腿分別合并為一條腿。在越障時不考慮轉向問題，因此可將越障運動視為平面運動。從而將四足機器人越障運動分析轉化為平面連桿機構的運動分析。

受到背越式跳高的啟發，本文對四足機器人翻轉式越障進行了運動規劃，如圖2所示。一個完整的運動周期包括5個階段：①從站立到前雙腿膝關節著地（圖2a）；②后雙腿越障（圖2b）；③機體姿態的調整（圖2c）；④前雙腿越障（圖2d）；⑤機器人正常站立（圖2e）。每個階段中機器人的開始姿態用實線表示，結束時的姿態用虛線表示。

機器人從左往右運動，前肢的踝關節、膝關節和髖關節分別用A、B、C表示；D、E、F分別表示后肢的髖關節、膝關節和踝關節。

3 運動學分析模型

四足機器人在翻轉式越障周期中，姿態會隨著不同的階段而變化，其運動學模型也要發生相應的變化。在以下的運動學分析中為了方便描述，以L1和L2分別表示前肢小腿和大腿，其長度分別用l1和l2表示；機體用L3表示，其長度用l3表示，O表示質心；后肢大腿和小腿分別用L4和L5表示，其長度分別用l4和l5表示。以θij表示機體或腿Li到Lj的逆時針夾角，當i或j為0時，表示直角坐標系x軸正向。以θ0ij表示一個運動階段的關節初始角，θ′ij表示該運動階段末時刻的關節角。

3.1 前雙腿膝關節著地階段

機器人從站立到前雙腿膝關節著地的位姿變換過程中，足底始終與地面保持接觸，足與地面無相對滑動，可把足底與地面的約束看作固定約束。機器人由站立到前雙腿膝關節著地的位姿變換過程如圖3所示，虛線所示為位姿變換完成時的姿態，取關節點F為原點，建立直角坐標系Fxy。

大腿與小腿長度相等，且為機體長度的一半，則

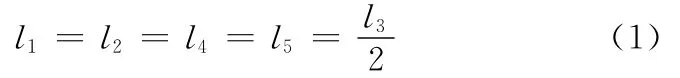
平面連桿機構的自由度計算公式：

式中，n為平面連桿機構的構件數目；pi為自由度為i的運動副數目。

由式（2）可得圖3中所示機構自由度f＝3，設定主動輸入為關節A、E和F。在圖3所示的前雙腿膝關節著地階段，各關節角的初始角度以及膝關節著地結束時的角度如表1所示。

表1 前雙腿膝關節著地階段的關節夾角 （°）

前雙腿膝關節著地的時間為0→ta，將輸入關節的速度均取勻速，則由表1中各個關節角的初始角以及末時刻夾角可得：

在圖3所示的位姿變換運動過程中，其運動回路矢量方程為

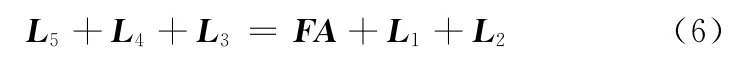
關節F到關節A的距離與l3相等，將式（6）寫成在直角坐標系Fxy中的標量形式為

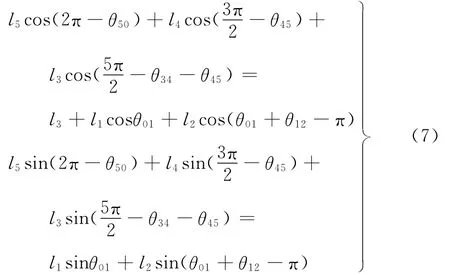
求解式（7）可得

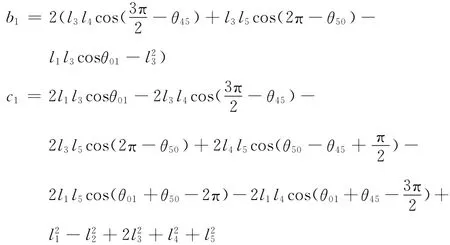
同理，求解式（7）可得：

另外，θ23的求解公式如下：

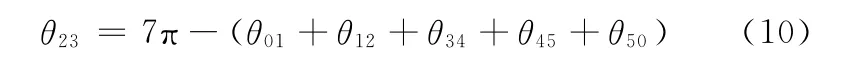
機器人由站立到前雙腿膝關節著地質心O的坐標公式如下：

3.2 后雙腿越障

在后雙腿越障階段，腿L1與腿L2固定，使其保持在前肢膝關節著地完成時的姿態，則后雙腿越障的運動學模型可簡化為一單開鏈平面四桿機構，取關節點B為原點，在其上建立坐標系Bxy，如圖4所示。

由圖4可以得出，在后雙腿越障過程中，各關節的初始角以及末時刻的角度如表2所示。

表2 后雙腿越障的關節夾角 （°）

由圖4所示的運動學模型以及式（2）可以得出腿L5的末端自由度f＝3。設定關節C、D、E為輸入關節，后雙腿越障的時間為ta→tb，且輸入均為勻速。為保證機器人的運動空間與障礙不發生干涉，使關節角θ45以及θ34先達到預定的值，再令關節C旋轉，則各關節的角度方程如下：

其中，tb1為關節C開始運動的時刻。關節角θ50分為兩個階段，θ50為270°→360°時為一個階段，θ50為360°→180°（即0→180°）時為一個階段，則

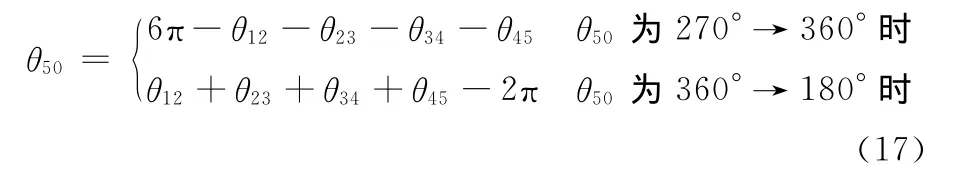
機器人在后雙腿越障過程中質心O的坐標為

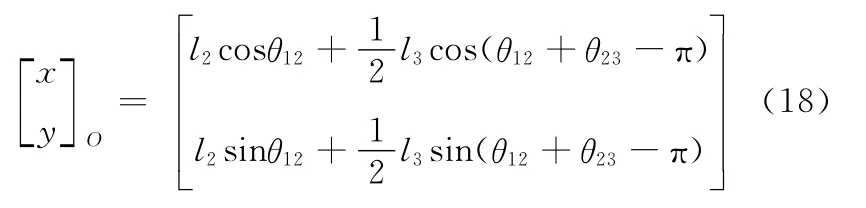
雙腿越障完成后，關節點B和E′之間的y軸方向距離即為機器人的越障高度h，其計算如下：

3.3 機體姿態調整

機體姿態調整階段，腿L5與地面平行接觸且無相對運動，腿L1的踝關節A與足僅有相對轉動，且足底與地面為固定約束。機器人運動簡圖可轉化為一單閉鏈平面五桿機構，取關節點A為原點，在其上建立直角坐標系Axy，如圖5所示。

由式（2）可知，機體姿態調整階段自由度f＝2，設定關節A、E為主動關節，其余關節為被動關節。機體姿態調整的時間為tb→tc。機體姿態調整的初始關節角及末時刻關節角見表3。

表3 機體姿態調整關節角 （°）

由機體姿態調整運動模型以及主動關節初始角和末時刻夾角，令

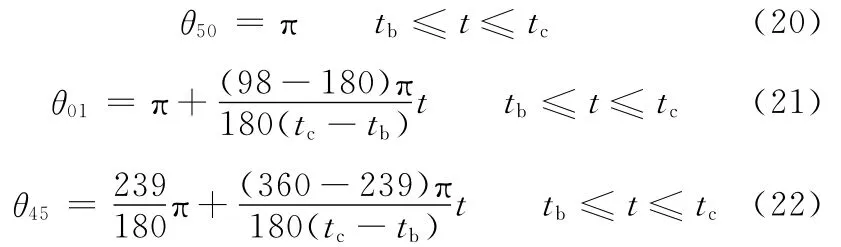
如圖5所示，機體姿態調整運動回路矢量方程為

將式（23）改寫為在坐標系Axy中的分量形式：

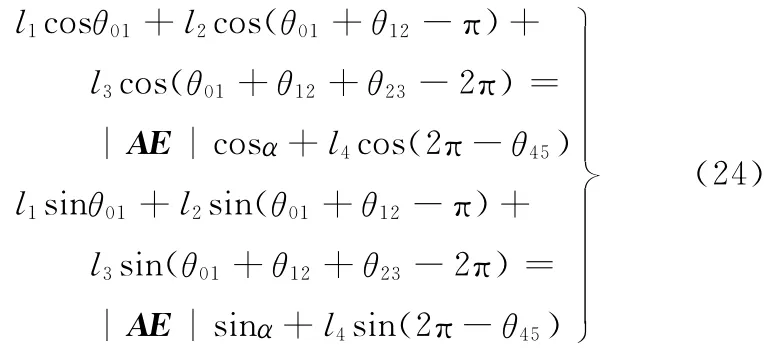
由式（24）可解得

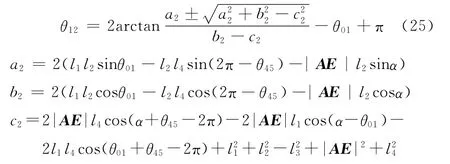
同理，可得

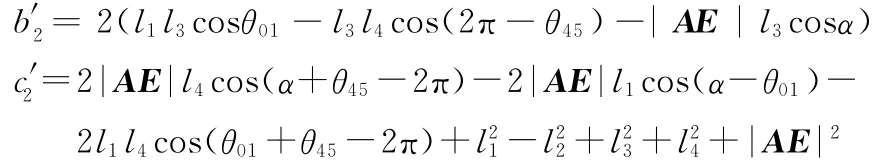
由圖5和圖4可知，在式（23）～式（26）中，有

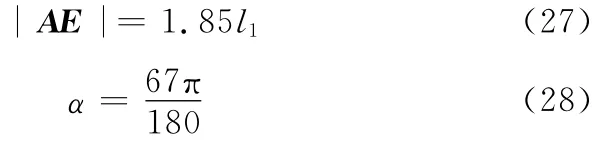
由圖5所示的運動關系，可得

θ34＝4π－（θ01＋θ12＋θ23＋θ45）（29）

機器人在機體調整階段質心O的坐標為

3.4 前雙腿越障

前雙腿越障階段，腿L5固定于地面，將腿L5取出，并令腿L1與腿L2之間的夾角θ12保持不變，則腿L4、機體L3以及腿L1與腿L2的組合是開鏈四桿機構，其自由度f＝3，取E關節點為原點，建立坐標系Exy，運動模型如圖6所示。

設定關節C、D、E為輸入關節，前雙腿越障作用時間為tc→td，其初始角以及末時刻的關節角見表4。

表4 前雙腿越障關節角 （°）

由初始角、末時刻角以及輸入關節運動關系，令

關節D和關節C同樣取勻速運動，可以保證工作過程中，質心O始終落在支撐范圍內，則

關節角θ01可分為兩個階段，當θ01為98°→0時為一階段，當θ01為0→142°（即360°→142°）時為一階段，則

前雙腿越障階段，機器人質心O的坐標為

3.5 機器人正常站立

機器人正常站立運動學模型如圖7所示，在關節點F建立坐標系Fxy。保持腿L1與腿L2的關節角θ12不變，則圖7所示機構的自由度f＝2，其運動學模型可看著單閉鏈平面五桿機構，設立關節A、F作為主動關節。正常站立時間為td→te，初始及末時刻關節角見表5。

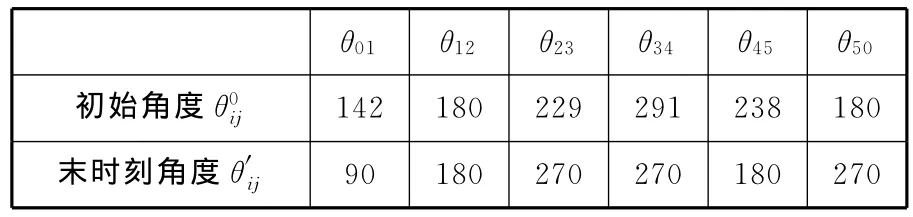
表5 正常站立關節角 （°）

正常站立過程中，腿L1與L2關節角θ12不變，并取關節A和關節F為勻速，則

如圖7所示，機器人正常站立運動回路矢量方程為

式（41）在坐標系Fxy中的標量形式為

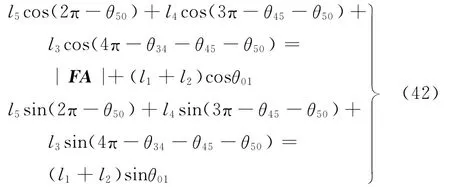
其中，關節F和關節A之間的距離：

｜FA｜＝l3（43）

由式（41）和式（42）可以解出：

同理，可得

而關節角θ23為

θ23＝6π－（θ01＋θ34＋θ45＋θ50）（46）

機器人質心O的坐標公式為

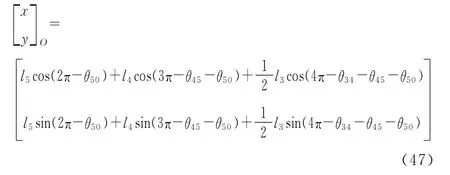
4 仿真分析

各關節角的角度方程建立后，根據式（1）取l1＝0.5m對機器人越障運動進行仿真。以翻轉式越障周期第一運動階段所建立的坐標系Fxy為基準，其余運動階段所設定的坐標系轉化到基準坐標系中。根據上文中的運動學分析模型，利用MATLAB編程計算可以得出機器人在翻轉式越障階段各關節角位移的變化曲線，如圖8所示，以及質心O的橫坐標和縱坐標變化曲線，如圖9所示。

5 越障能力分析

越障能力和機器人的幾何參數、運動方案以及越障時機器人與障礙物的距離有關，下面討論在現有的幾何參數并在規劃的運動方案下機器人的越障能力。

機器人在整個翻轉式越障周期中，機體翻轉階段有兩個：后雙腿越障和前雙腿越障階段。機體在兩次翻轉過程中需保證機體質心O在支撐面內。在后雙腿越障階段（圖4），質心O必須在支撐面內，即

在前雙腿越障階段（圖6），機器人質心O必須在支撐面內，即

由圖9所示的變化曲線可以看出該運動方案滿足翻轉條件。綜合關節角的運動空間、機械結構參數等可以得出機器人的最大越障高度為

則后雙腿翻轉越障完成時，機器人的機體L0、腿L3以及腿L4重合。

6 結束語

為了提高四足機器人的越障能力，本文提出一種基于機體翻轉的臺階翻越方式，并對其進行了運動規劃和運動學仿真分析。分析中將機器人的結構簡化為平面連桿機構，使得仿真分析變得簡單。在給定輸入規律的情況下，得出了翻越臺階過程中各關節的角位移變化曲線以及重心的移動軌跡，從運動學角度驗證了該越障方法的有效性和可行性。本文對足式機器人的越障方式進行了有益的探索，為進一步的研究提供了理論基礎。

［1］陳學東，孫翊，賈文川.多足步行機器人運動規劃與控制［M］.武漢：華中科技大學出版社，2006.

［2］黃博，王鵬飛，孫立寧.基于行為模式的復合運動方式四足機器人研究［J］.中國機械工程，2007，18（18）：2159－2162.

［3］劉靜，趙曉光，譚民.腿式機器人的研究綜述［J］.機器人，2006，28（1）：81－88.

［4］Takahashi M，Yoneda K，Hirose S.Rough Terrain Locomotion of a Leg－wheel Hybrid Quadruped Robot［C］／／IEEE Int.Conf.on Robotics and Automation.Orlando，USA，2006：1090－1095.

［5］張力平，馬書根，李斌，等.可重構模塊化機器人系統的翻越臺階能力研究［J］.中國機械工程，2009，20（12）：1407－1412.

［6］王婧，李斌，馬書根，等.模塊化可變形機器人控制系統設計與變形方法研究［J］.機器人，2006（9）：457－462.

［7］Phipps C C，Shores B E，Minor M A.Design and Quasi－static Locomotion Analysis of the Rolling Disk Biped Hybrid Robot［J］.IEEE Transactions on Robotics，2008，24（6）：1302－1314.

［8］Yim M，Zhang Y，Roufas K.Connecting and Disconnecting for Chain Self－reconfiguration with Polybot［J］.IEEE／ASME Transactions on Mechatronics，2002，7（4）：442－451.

［9］Murphy R，Casper J，Hyams J.Mobility and Sensing Demands in USAR［C］／／IEEE Industrial Electronics Conference.Piscatoway，USA，2000：138－142.

［10］畢樹生，張利格.具有并聯機構的四面體翻滾機器人：中國，200910093258.X［P］.2010－03－10

［11］孔德隆，劉偉，徐文勝，等.一種滾動三角形機器人：中國，200910076337.X［P］.2009－10－21.