用計量型AFM對一維納米基準(zhǔn)柵的標(biāo)定及不確定度估計

黃強先 袁 丹 尤煥杰

合肥工業(yè)大學(xué)，合肥，230009

0 引言

隨著微加工技術(shù)、MEMS技術(shù)和納米技術(shù)的發(fā)展及應(yīng)用，利用這些技術(shù)加工或制備的微器件、MEMS器件及納米材料等幾何尺寸越來越小，相應(yīng)地對測量精度要求越來越高，甚至要求達到納米量級及亞納米量級。目前，已具有納米量級甚或亞納米量級分辨率的儀器，如原子力顯微鏡（AFM）、掃描隧道顯微鏡（STM）和掃描電子顯微鏡（SEM）等各種納米量級測量儀器。上述測量儀器被廣泛應(yīng)用于各種器件需求的測量領(lǐng)域。盡管上述儀器具有極高的空間分辨率，甚或能夠分辨出表面原子的位置，但由于上述儀器的測量范圍小、測量分辨率高和測量不確定度要求極高，導(dǎo)致上述儀器的精確標(biāo)定成為目前的世界難題［1－3］。為了方便、可靠地標(biāo)定上述測量儀器，國際計量局（BIPM）在1998年把納米尺度線間隔、臺階高度、線寬等5個參數(shù)的計量確定為納米尺度基本特征國際關(guān)鍵比對項目之一［4］，并提出了相應(yīng)的5種基準(zhǔn)樣板，以便測量者基于基準(zhǔn)樣板特征參數(shù)確定儀器的測量不確定度。

一維納米基準(zhǔn)柵樣板是5個納米標(biāo)準(zhǔn)樣板之一［4］，其平均柵距是該基準(zhǔn)樣板的特征參數(shù)，目前的制作精度達到納米量級［3，5］。對于該基準(zhǔn)柵柵距的標(biāo)定，既要具有亞納米量級的測量不確定，又必須使其測量結(jié)果溯源到長度基準(zhǔn)，目前一般采用計量型原子力顯微鏡、光學(xué)衍射儀等儀器進行標(biāo)定［1，4，6］。不管采用何種方法和儀器［7］，由于測量儀器復(fù)雜、測量環(huán)境要求高、測量對象自身加工精度高，以及平均柵距不能直接與長度基準(zhǔn)比較，給測量工作帶來諸多不便。為了獲得可靠的測量結(jié)果，需要對測量過程中的各種測量不確定因素進行充分和可靠的分析，從而獲得精確的測量結(jié)果的測量不確定度。針對輕敲模式計量型AFM的結(jié)構(gòu)特點［8］，本文介紹公稱柵距為240nm的一維基準(zhǔn)柵的標(biāo)定，并對其結(jié)果進行不確定度分析和估計。

1 一維基準(zhǔn)柵與計量型原子力顯微鏡

1.1 一維基準(zhǔn)柵

國際計量局（BIPM）的納米計量工作組（WGDM7DG）在1998年決定把線寬（Nano 1）、臺階高度（Nano 2）、線刻度尺（Nano 3）、一維柵（Nano 4）和二維柵（Nano 5）作為納米尺度比對的5種基準(zhǔn)樣板。本文所采用的一維基準(zhǔn)柵是由Hitachi Ltd開發(fā)的 HJ－1000標(biāo)準(zhǔn)樣板［9］，主要用于納米測量儀器的標(biāo)定。該樣板是通過激光干涉全析法和各向異性化學(xué)刻蝕技術(shù)制備的硅樣板，樣板的實物圖及公稱尺寸如圖1所示。該標(biāo)準(zhǔn)柵的特征參數(shù)是平均柵距，公稱值為240nm，其制造精度為1nm（3σ）。樣板的有效面積約為4mm×4mm。為了便于使用，硅樣板被固定于鋁金屬基板上。

1.2 計量型原子力顯微鏡

圖2所示為AFM系統(tǒng)構(gòu)成框圖，圖中，LD為激光二極管，QPD為四象限光電二極管，TSM為三維反射鏡載物臺。AFM系統(tǒng)由機械系統(tǒng)、懸臂信號處理系統(tǒng)、控制系統(tǒng)、測量系統(tǒng)和控制、數(shù)據(jù)處理及顯示系統(tǒng)等五部分組成［8］。該測量系統(tǒng)與帶有閉環(huán)控制系統(tǒng)的AFM結(jié)構(gòu)基本相同。所不同的是，該計量型AFM的載物臺是由石英材料制作的，且其上方的開口為方槽，如圖3所示。該載物臺置于三維工作臺的上方。載物臺的下表面和兩相鄰側(cè)面正交，并鍍有反射膜，因此被稱為三維反射鏡（TSM）。三反射鏡正交性很好，其垂直度誤差在1″以內(nèi)。載物臺在x、y、z三維的運動分別用高精度的穩(wěn)頻氦氖激光邁克爾遜干涉儀測量，3個正交反射面分別作為3套干涉測量儀的測量反射鏡（圖3），因此，載物臺在x、y、z方向上的位移測量結(jié)果可以長度標(biāo)準(zhǔn)溯源。載物臺在x、y方向的位置通過激光干涉儀的位移信號反饋控制，從而完全克服了工作臺中壓電驅(qū)動器非線性、遲滯等的影響。三激光干涉儀的測量線分別與試樣的x、y、z運動方向一致，且三測量線正交于AFM探針的針尖處，因此基本消除了阿貝誤差。

在每一路激光干涉儀中，測量光路經(jīng)過4倍光學(xué)放大，光信號經(jīng)過光電轉(zhuǎn)換后又通過軟件進行了2048相位細分，即干涉儀的每一個干涉條紋的周期變化與八分之一激光波長的TSM移動量相對應(yīng)，每一個細分脈沖的變化與工作臺的λ／16 384位移量相對應(yīng)，因此，經(jīng)信號處理系統(tǒng)處理后的干涉測量系統(tǒng)的分辨率可達到0.04nm。經(jīng)實驗觀測，該激光測量系統(tǒng)的非線性誤差約為0.12nm，是影響精度的主要誤差源之一。

該計量型AFM的x、y、z測量范圍分別為17.5μm、17.5μm、2.5μm。該系統(tǒng)原來僅能工作于接觸模式，且測量效果不理想，改進后的系統(tǒng)可工作于測量時一般采用的輕敲模式［8］。

2 測量過程與數(shù)據(jù)預(yù)處理

2.1 測量方法與測量過程

一維柵的柵線在4mm×4mm上分布，分布面積較大，實驗發(fā)現(xiàn)，各處的柵距存在微小的差異。而AFM的掃描區(qū)域很小，一般僅為數(shù)微米至十微米。為了減小樣板均勻性的影響，測量時在樣板表面均勻選擇9處進行測量，如圖4所示。

為了減小阿貝誤差，在載物臺上安放樣板時，應(yīng)使被測量區(qū)域處于三激光干涉儀的測量延長線的交點處。該計量型AFM在掃描一維柵時，采用圖5所示的掃描方式，即硅懸臂與一維柵的柵線方向一致。因此，樣板還應(yīng)按照圖5所示的方向安放，并盡可能地使柵線方向與y方向平行。圖6所示為獲得的一個區(qū)域的三維圖。

測量時，AFM的環(huán)境溫度、濕度、大氣壓以及工件的溫度等環(huán)境參數(shù)被實時記錄，以用于對計算數(shù)據(jù)的補償和不確定度分量的估計。

2.2 數(shù)據(jù)處理

測量時，每一區(qū)域的掃描范圍是5μm×5μm，共進行30行掃描、每行獲取11 000個點。盡管測量時工作臺的x、y位移利用激光干涉儀信號進行閉環(huán)反饋控制，但并不能完全消除壓電陶瓷的遲滯、蠕變等非線性影響［8］，這種影響在每一掃描區(qū)域的開始數(shù)行和每行的起始端較大。為了減小對測量結(jié)果的影響，在進行數(shù)據(jù)處理時，每一掃描區(qū)域的前10行和每行的前后500個點不參與柵距的計算。

AFM探針在掃描樣板時，由于樣板的安放誤差，探針的掃描方向不可能完全與柵距的方向一致，存在垂直傾角θ和水平偏轉(zhuǎn)角α安裝誤差（圖6）。為了減小這兩項角度誤差的影響，必須對原始數(shù)據(jù)進行處理。

圖7a所示為樣板垂直傾角誤差的校正方法。首先，按照線輪廓的頂點確定線輪廓的中心線傾角，該角度被認為就是樣板在垂直方向上的安放誤差。然后，根據(jù)所確定的垂直傾角θ對原始數(shù)據(jù)進行校正，得到圖7a中的中間線輪廓，再根據(jù)校正后的線輪廓，按照重心法確定各個柵峰的重心點橫坐標(biāo)［10］。

當(dāng)每條掃描線上的每個柵峰重心被確定后，即可擬合出圖7b所示的柵線方向，該方向與y向的夾角，就是樣板在水平面內(nèi)安放時的偏轉(zhuǎn)誤差α，該角度誤差將帶給柵距計算誤差。為了縮小該誤差，需要將圖7b中左圖的重心線校正到中間圖的位置，再根據(jù)校正后的各重心點確定出各個柵距pi（圖7b）。在計算時，上述過程的殘余誤差將構(gòu)成兩項測量不確定度分量。

通過上述數(shù)據(jù)處理后的平均柵距為

式中，n為掃描區(qū)域內(nèi)柵距的個數(shù)。

表1所示為按照上述測量和數(shù)據(jù)處理方法，獲得的9個區(qū)域的算術(shù)平均值及相應(yīng)的單次測量不確定度。

表1 9個不同測量區(qū)域的平均柵距、單柵距標(biāo)準(zhǔn)差和平均柵距標(biāo)準(zhǔn)差

根據(jù)表1中的數(shù)據(jù)，9個區(qū)域內(nèi)所有柵距的平均值為240.078nm。

3 不確定度因素分析及估計

利用上述系統(tǒng)按照上述測量過程和數(shù)據(jù)處理方法，對一維基準(zhǔn)柵柵距進行測量、計算，測量結(jié)果主要受下面各項因素的影響并導(dǎo)致相應(yīng)的不確定度分量：

（1）激光頻率變化引起的測量不確定度分量u1。穩(wěn)頻氦氖激光器為Spectra－Physics，Model 117A，其Allan方差頻率是124kHz，當(dāng)該數(shù)值變化不大于5%時，導(dǎo)致的柵距測量不確定度分量u1為12.1pm，自由度為200.0。按照B類評定方法確定。

（2）溫度變化引起的激光死程變化導(dǎo)致的測量不確定度分量u2，該部分是由激光底座溫度變化導(dǎo)致底座在激光死程部分熱膨脹變化引起的。經(jīng)測定，溫度變化不超過3.2K時，底座可采用因瓦合金制作。經(jīng)估計，該部分引起的標(biāo)準(zhǔn)不確定分量為1.17fm，自由度為12.5。按照B類評定方法確定。

（3）阿貝誤差引起的測量不確定度分量u3。設(shè)計時，要求激光干涉儀的測量光路與探針的掃描方向在同一條直線上。但在安裝和使用時，由于探針長度不同及其安裝誤差，會導(dǎo)致兩者之間存在最大不超過0.5mm的偏差。經(jīng)測量，工作臺的隨機運動誤差為0.283×10－2″，近似符合均勻分布。按照B類評定方法估計，該部分引起的標(biāo)準(zhǔn)不確定分量為40.9pm，自由度為200.0。

（4）光路準(zhǔn)直誤差引起的測量不確定度分量u4。在AFM結(jié)構(gòu)中，激光干涉儀的測量光路應(yīng)該與干涉儀測量鏡反射面完全垂直，但在安裝時存在最大｜±0.085°｜的準(zhǔn)直誤差，該誤差將導(dǎo)致工作臺位移測量時的余弦誤差。該部分引起的測量結(jié)果標(biāo)準(zhǔn)不確定分量為16.9fm，自由度為200.0。

（5）光路變化引起的測量不確定度分量u5。在測量時，由于工作臺運動誤差的存在，除了引起阿貝誤差外，還會導(dǎo)致干涉儀反射鏡的角位移。而干涉儀反射鏡的角位移會使反射光路的變化不穩(wěn)定，從而導(dǎo)致長度測量誤差，該誤差為二次誤差。按照B類評定方法估計，該部分引起的測量結(jié)果標(biāo)準(zhǔn)不確定分量為2.06pm，自由度為200.0。

（6）干涉儀非線性誤差u6。干涉儀經(jīng)過8倍光學(xué)細分后，還經(jīng)過2048次相位細分，由于光路、電路等的不理想，由干涉儀輸出的正交電信號并不能構(gòu)成理想的Lissajow圖形，從而造成周期性的非線性誤差，如圖8所示。按照B類評定方法估計，該誤差引起的測量結(jié)果標(biāo)準(zhǔn)不確定分量為0.115nm，自由度為200.0。

（7）激光干涉儀分辨率引起的測量不確定度分量u7。根據(jù)技術(shù)資料，激光干涉儀經(jīng)過8倍光學(xué)細分和2048次電子細分后，按照B類評定方法估計，其導(dǎo)致的柵距測量不確定度分量u7為38.6pm，自由度為200.0。

（8）環(huán)境溫度、濕度和氣壓變化引起的測量不確定度分量u8、u9、u10。測量光路周圍大氣參數(shù)的變化將導(dǎo)致光路上大氣折射率的變化，從而導(dǎo)致激光頻率和波長的變化，引起測量誤差。通過實時監(jiān)測，當(dāng)環(huán)境的溫度、相對濕度和大氣壓的變化不超過1.20K、3.50%和1.50kPa時，由 Edlen公式估計的環(huán)境溫度、濕度和氣壓變化引起的測量不 確 定 度 分 量 分 別 為 0.157pm、5.18fm 和0.154pm，按照測試儀器說明，自由度取為12.5。

（9）樣板熱膨脹引起的測量不確定度分量u11。樣板安裝在工作臺上，由于壓電陶瓷管的發(fā)熱、硅探針振幅檢查光路熱源等因素的影響，導(dǎo)致了被測尺寸的變化。經(jīng)實際測量，樣板偏離標(biāo)準(zhǔn)室溫20℃的最大溫差不超過3.2℃，硅樣板材料的熱膨脹系數(shù)為2.6×10－6K－1，溫度變化符合均勻分布要求。根據(jù)測試儀器說明，按照B類評定方法估計，由樣板熱變形導(dǎo)致的測量不確定度分量為1.15pm，自由度為12.5。

（10）樣板安裝誤差引起的測量不確定度分量u12、u13。在圖7中，雖然通過數(shù)據(jù)處理可以校正樣板2個放置角度帶來的主要影響，但由于20行掃描數(shù)據(jù)的不一致，導(dǎo)致其修正結(jié)果分散。通過測量數(shù)據(jù)分析，按A類評定得到這兩項誤差帶來的不確定度分量分別為1.02pm和1.36pm，自由度為19.0。

（11）重復(fù)性引起的測量不確定度分量u14。通過對樣板同一測量區(qū)域的7次重復(fù)測量，得到的單次測量標(biāo)準(zhǔn)差為11.2pm，該標(biāo)準(zhǔn)差可視為重復(fù)性引起的測量不確定度分量（按A類評定），自由度取為6.0。

（12）樣板各處均勻性引起的測量不確定度分量u15。由于制備工藝原因，樣板表面各處的柵距值不一致。為避免不均勻性的影響，一般采用樣板內(nèi)多處均勻取點測量，本文采用了9處取點測量（圖4）。將各處不同點的平均值差值標(biāo)準(zhǔn)差作為樣板均勻性誤差引起的測量不確定度分量，本次測量結(jié)果為83.6pm（按A類評定），自由度取為8.0。

（13）區(qū)域平均柵距誤差引起的測量不確定度分量u16為0.102nm。在本次測量中，測量范圍約為5μm×5μm，用其中獲得的20行進行平均柵距計算，每行約有21個柵距，共約有420個柵距參與本區(qū)域內(nèi)的平均柵距計算。分析表明，本區(qū)域內(nèi)的柵距分布直方圖與圖9所示類似。圖9是一個測量區(qū)域柵距的分布情況，共有420個柵距，其平均柵距為240.13nm，單個柵距的標(biāo)準(zhǔn)差為2.096nm，平均柵距的標(biāo)準(zhǔn)差為0.102nm。該標(biāo)準(zhǔn)差是區(qū)域平均柵距的測量不確定度分量（按A類評定），自由度取為419.0。

表2所示為各個因素對測量結(jié)果的影響，以及各因素所導(dǎo)致的不確定度分量、評定類型和自由度。在上述各項影響因素中，一般來說，相關(guān)性很低或者不相關(guān)，且各因素都對平均柵距有直接影響，因此，可按照下述方法確定合成標(biāo)準(zhǔn)不確定度和自由度：

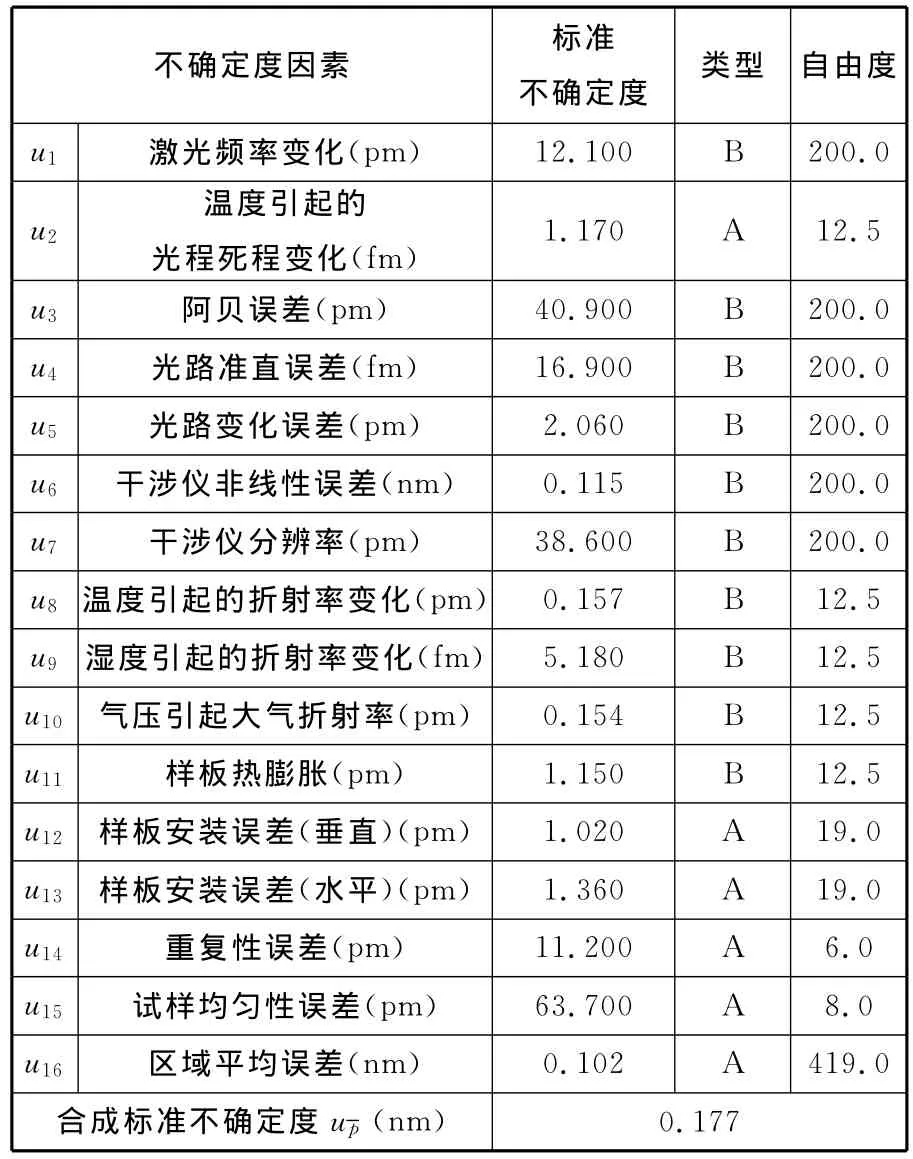
表2 測量結(jié)果不確定度分量表

若置信概率取為95%，則平均柵距的擴展不確定度約為0.347nm，其測量結(jié)果為（240.078±0.347）nm。

根據(jù)上述分析和計算結(jié)果，計量型AFM對一維標(biāo)準(zhǔn)柵的標(biāo)定達到了亞納米量級精度。同時通過分析發(fā)現(xiàn)，在影響測量結(jié)果的各個不確定度分量中，除了試樣均勻性誤差、區(qū)域平均誤差等一維樣板自身具有的誤差外，儀器結(jié)構(gòu)的阿貝誤差、自身的非線性誤差、穩(wěn)頻誤差和分辨率、測量過程中的安裝誤差和環(huán)境變化等，都是不可忽略的影響測量不確定度的因素。另外，在進行納米量級測量時，一些常規(guī)測量中可以忽略的誤差，如光路變化誤差、準(zhǔn)直誤差等二次誤差，也需要充分考慮。

4 結(jié)束語

在對輕敲模式計量型原子力顯微鏡及一維基準(zhǔn)柵結(jié)構(gòu)和特性充分了解的基礎(chǔ)上，用計量型AFM對一維基準(zhǔn)柵的特征參數(shù)平均柵距進行了測量。通過對AFM結(jié)構(gòu)和特性參數(shù)、一維基準(zhǔn)柵特性和參數(shù)、測量過程參數(shù)、數(shù)據(jù)處理方法的全面分析，給出了基準(zhǔn)柵的平均柵距及測量不確定度分析和估計，擴展不確定度達到0.347nm（擴展因子k＝1.96）。本文測量和分析表明，測量不確定度的確定，不僅需要充分了解測量儀器的結(jié)構(gòu)和參數(shù)，而且需要充分了解測量過程中各種參數(shù)對測量不確定度的影響；而對于納米量級測量，常規(guī)測量過程中一些可以忽略的二次誤差也需要考慮。

［1］Misumi I，Gonda S，Sato O，et al.Nanometric Lateral Scales as CRM Candidates for AFM，SEM and Optical Diffractometer［J］.J.Phy.：Conference Series，2005，13：206－215.

［2］Ritter M，Dziomba T，Kranzmann A，et al.A Landmark－based 3DCalibration Strategy for SPM［J］.Meas.Sci.Technol.，2007，18：404－414.

［3］Nakayama Y，Yamamoto J，Kawada H.Sub－50－nm Pitch Size Grating Reference for CD－SEM Magnification Calibration［C］／／Proceedings of Me－trology，Inspection，and Process Control for Microlithography XXIII.San Jose，USA，2009：727224.

［4］Meli F.WGDM－7：Preliminary Comparison on Nanometrology According to the Rules of CCL Key Comparisons，Nano4：1DGratings，F(xiàn)inal Report［R］.Wabern：Swiss Federal Office of Metrology（OFMET），2000.

［5］Nakayama Y，Kawada H，Yoneda S，et al.Novel CD－SEM Calibration Reference Consisting of 100－nm Pitch Grating and Positional Identification Mark［C］／／Proceedings of Metrology，Inspection，and Process Control for Microlithography XXV.San Jose，USA，2011：797119.

［6］Ito Y，Omote K，Okazaki Y，et al.Calibration of 25－nm Pitch Grating Reference by High－resolution Grazing Incidence x－ray Diffraction［C］／／Proceedings of Metrology，Inspection，and Process Control for Microlithography XXIV.San Jose，USA，2010：763810.

［7］Decker J E，Eves B J，Pekelsk J R，et al.Evaluation of Uncertainty in Grating Pitch Measurement by Optical Diffraction Using Monte Carlo Methods［J］.Meas.Sci.Technol.，2001，22（2）：027002

［8］Huang Qiangxian，Gonda S，Misumi I，et al.Nonlinear and Hysteretic Influence of Piezoelectric Actuators in AFMs on Lateral Dimension Measurement［J］.Sens.Actuat.A，2006，125：590－596.

［9］Nakayama Y，Toyoda K.New Submicron Dimension Reference for Electron－beam Metrology System［C］／／Proceedings of Metrology，Inspection，and Process Control for Microlithography III.San Jose，USA，2010：219674.

［10］Huang Qiangxian，Gonda S，Misumi I，et al.Research on Pitch Analysis Methods for Calibration of One－dimensional Grating Standard Based on Nanometrological AFM［C］／／Proceedings of SPIE 6280.Third International Symposium on Precision Mechanical Measurements.Urumiqi，China The International Society for Optical Engineering：2006：628007.