靜電微泵的3D流固耦合動態特性分析

董金新 林謝昭 應 濟 李 俊

1.溫州職業技術學院，溫州，325035 2.浙江大學，杭州，310027

0 引言

微流體系統中大都要求有微泵。其中，薄膜往復振動式無閥微泵是以擴散／收縮單元為閥門，通過泵膜的振動驅動流體，其制造簡單，可以驅動一些非均相的流體，是眾多研究的焦點。根據驅動原理不同，無閥微泵可劃分為電磁、靜電、壓電、形狀記憶合金等多種類型。其中，靜電無閥微泵具有較低功耗，易于與IC工藝集成兼容等優點，而得到廣泛關注。

由于微泵的尺度很小，薄膜往復振動式無閥微泵的絕大部分物理量難以通過實驗測量，特別是瞬態量。因此，在微泵的研制階段，利用數值方法對動態性能進行仿真、預測顯得很重要。它不僅可降低費用，而且能更好地了解微泵的工作原理以及可能的潛在缺陷。但因微泵中柔性泵膜、電驅動和流體相互耦合，加之流體在擴散／收縮單元中的不同流動方向表現出的不同壓力特性，增加了對整個泵的仿真難度和復雜性。早期的研究采用低階集總參數模型［1－2］和等效電網絡模型［3］等簡化方法，忽略了參數的空間分布特性。目前大部分的研究沒有考慮泵的流固耦合效應，也無法建立電驅動信號量與流體動力學量（比如流量）之間的關系。或是研究驅動器的動態特性［4－7］；或是簡化流體場，根據擴散／收縮單元的壓力損失系數，將泵膜的運動與泵腔內外壓力以及擴散／收縮單元流量聯系起來，研究泵膜的動態特性［8－11］；或是將驅動器的位移輸出，作為流體場的移動壁面問題來研究泵流體的動力學特性［12－14］。實際上，泵膜的動態特性與流體黏滯損失的非線性和不穩定性等是相互影響的。為了理解整個微泵的動態特性，模型必須能有效地描述這些耦合效應［15－16］。本文以靜電無閥微泵為對象，建立靜電－結構－流體全耦合的3維模型，利用數值方法，仿真并分析各個變量的非線性動態特性。

1 模型的建立

1.1 控制方程、邊界條件以及初始條件

圖1所示為靜電無閥微泵的結構示意圖。對于泵送流體，采用任意拉格朗日－歐拉（ALE）描述比較方便。某一時刻，在參考系中＾x位置流動的流體質點速度u的時間導數可以表示為

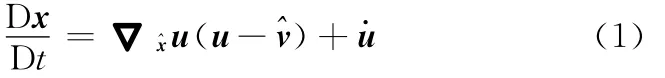
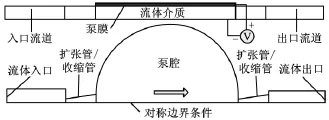
圖1 靜電無閥微泵的結構示意圖

流體域Ωf的不可壓縮流動動量守恒定律以及連續方程可以表示為

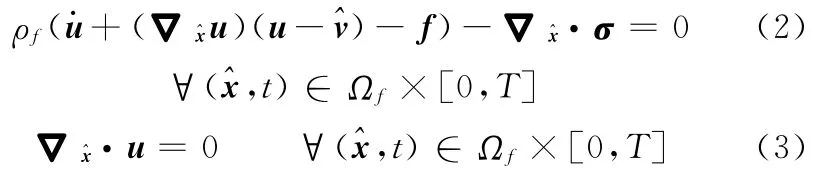
式中，ρf、f、σ分別為流體密度、體積力向量和Cauchy應力張量；［0，T］為所考察的時間間隔。

牛頓流體的本構方程為

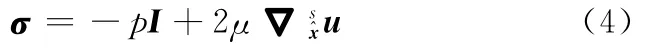
在泵膜流固耦合界面Γf－s處，邊界條件如下：

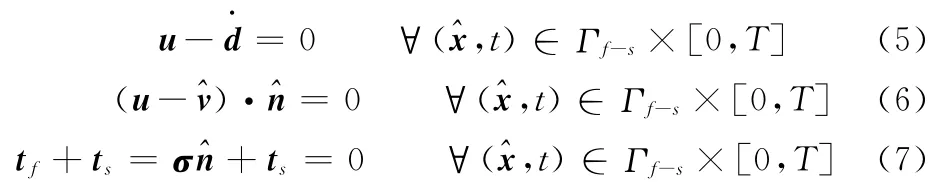
式（5）為流固界面Γf－s處的無滑移條件；在流固界面Γf－s上，參考系的速度＾v及其位置＾x需要滿足連續條件式（6），以保證參考系的邊界準確地表達結構的當前構型。沿著界面的應力平衡由式（7）表達。

對于泵膜，可以利用標準的Lagrangian描述建立其運動學方程，即

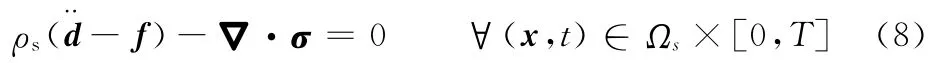
式中，ρs為固體的密度。

泵膜流固耦合邊界Γf－s滿足：

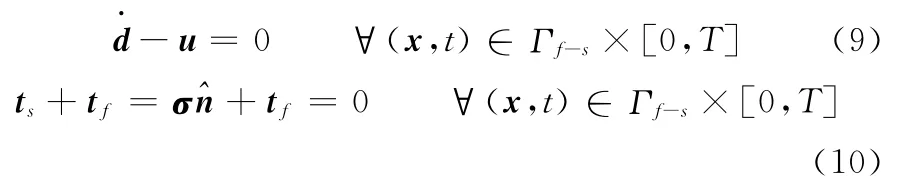
邊界條件式（9）、式（10）分別對應于式（5）和式（7）。

如果沒有包含自由電荷，則描述靜電場的Poisson方程可以表示為

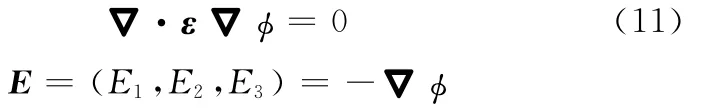
式中，φ為靜電勢；ε為介電常數張量；E為靜電場電場強度。

Maxwell靜電應力張量TE由下式計算：

式中，FE為靜電載荷。

各個場變量的初始條件都設置為零。為了計算易于收斂，將一個很小的初值輸入到模型中。

1.2 模型參數及材料屬性

圖1所示靜電微泵的泵膜厚度為10μm，泵腔深度為100μm，泵膜半徑為2000μm；擴散／收縮單元的幾何結構相同，長度為1000μm，最小端面寬度尺寸為80μm，擴張角為10°；連接的進出口管道長度皆為2000μm，寬度為200μm。流體介質為去離子水，物性參數如表1所示。

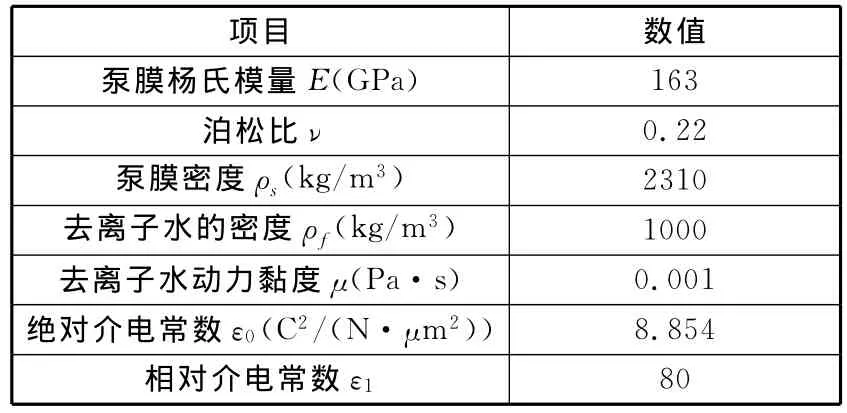
表1 與微泵仿真相關的材料屬性參數

假設層流流動，考慮對稱性，在CFD－ACE中建立微泵的一半模型。利用結構化網格劃分流體，單元數為52 880個，泵膜劃分為4974個殼單元。使用基于壓力修正的SIMPLE－C 算法對流動以及能量進行順序積分，獲得流場的解。流體域的對流和擴散采用一階迎風格式，時間積分采用了Crank－Nicolson格式。使用基于有限體積法的計算格式求解靜電場，這樣可以處理不同介質介電常數問題。利用一階殼單元來表達泵膜，并進行大變形和接觸等幾何非線性分析。考慮到靜電、結構以及流動耦合求解的需要，利用網格重劃分工具，使用預測－校正方法對局部變形進行連續修正，將流動速度和結構速度聯系起來，實現流固耦合分析。流體和結構求解器的耦合迭代頻率設置為fc＝1，使得流體場和結構場信息能及時得到交換和更新。當量綱一殘差小于10－4時，認為計算是收斂的。施加的周期性驅動電壓V＝200（1－cos（20πt））（泵腔底電壓為零），在Pentium－3.0GHz的PC機中，完成3.5個周期的求解，共350個子步數，求解時間約為59h。

2 結果及討論

2.1 泵膜的動力學特性

圖2所示為計算得到的泵膜中心點垂直方向上的位移隨時間變化曲線，圖中最大變形量為28.433μm。考慮流固耦合效應后，在流體阻尼作用下，泵膜無法回復至初始零位置，0.653μm為新的平衡位置。穩態情況下，泵膜位移的變化滯后于輸入電壓信號的變化，一個周期的滯后時間約為0.01s。

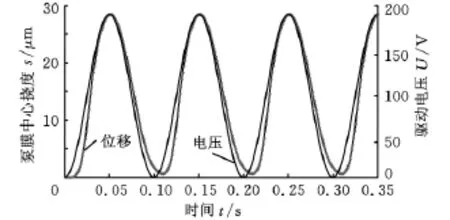
圖2 泵膜中心垂直方向上的位移隨時間變化曲線

2.2 流場的瞬態特性

實際上，泵流體動態特性更為設計者所關注，為了更好地詮釋泵膜振動與流體特性之間的耦合關系，用圖3所示的泵膜流固耦合界面上中心點處的垂直方向位移與泵腔內流體壓力來顯示其對應關系，從圖中可以明顯地看出，流體壓力的變化與泵膜的位移存在著密切關系。在靜電力的作用下，泵膜下拉變形的速度大于回彈的速度，所以在流體壓出泵腔的過程中其壓力變化較大，最高壓力為945.1Pa；而在流體吸入泵腔過程中，其壓力變化相對較小，最大負壓為－558.0Pa；整個泵送過程中，流體壓力呈現非對稱性變化。圖3還表明，泵初始工作點從零點開始，經過第一個周期的瞬態過程后，第二個周期的軌跡與第三個周期的軌跡已經重合，表明泵已經進入穩定工作狀態。流體壓力的波動周期同樣滯后于驅動電壓的變化（約0.01s）。

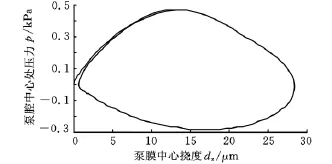
圖3 泵膜中心點處垂直方向上位移與流體壓力的關系

圖4所示為進出口單元處的瞬態體積流量變化曲線，從圖中可以看出，在泵膜下拉（往固定電極）運動階段（泵送階段），出口單元的瞬態流量大于進口單元的瞬態流量；而在泵膜回彈階段（泵吸入階段），進口單元的流量則大于出口單元的流量。最大的瞬態流量差發生在泵腔內壓力達到極大值時刻，而在泵腔內壓力與進出口壓力相差不大的時間段，進出口單元的流量相差不大。表明要使擴散／收縮單元發揮“整流”作用，其兩端的壓力差必須達到一定值，并且壓力差要盡可能地大。對穩態情況下的泵凈流量進行積分計算，得到的凈輸出流量為10.764nL／s。

圖4 進出口瞬態流量隨時間的變化

圖5所示為微泵橫截面方向上流體壓力的分布情況，由圖可知泵腔內的壓力幾乎分布一致，說明在平面布置的無閥微泵中，采用Reynolds方程來描述泵腔內流體的瞬態動力學特性具有一定的可行性。另外，微泵所連接的進出口管道對微泵的工作性能也有影響。

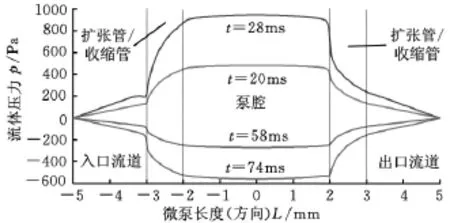
圖5 不同時刻下的微泵橫截面方向上的壓力分布情況

考慮了流固耦合特性后，模型不僅能夠仿真泵流場的動態特性，還能夠仿真泵膜的應力特性變化。圖6所示為t＝28ms時刻的泵腔內流體壓力分布與泵膜應力分布情況，以及這一時刻的擴散／收縮單元內流體的速度場分布。此時，泵腔內流體壓力達到最大值945.3Pa，泵膜中心撓度為13.20μm；泵 膜 邊 緣 處 VonMises 應 力 為28.39MPa。微泵腔內的流速較小，擴張管／收縮管頸部的平均流速達到最大，計算得到的平均流速為0.0867m／s，雷諾數為7.71，遠小于宏觀條件下通常認定的臨界雷諾數（2000左右），這也證實了前面假設層流流動模式的正確性。另外，圖6b和圖6c表明，收縮／擴散管內未出現流體與固體壁面分離流動現象。

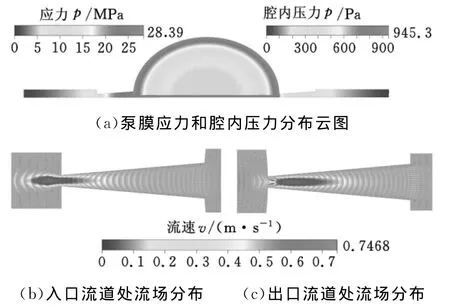
圖6 t＝28ms時刻的泵膜應力和微泵的流體場瞬態結果

3 結論

（1）擴散／收縮單元的最大流量差都發生在泵腔內壓力與進出口壓力相差最大的時刻，表明要使得擴散單元發揮“整流”作用，其單元兩端的壓力差必須達到一定值。

（2）在仿真的每個時刻，泵腔內流體壓力分布幾乎一致，表明用Reynolds方程來描述泵腔內流體動力學特性具有可行性。

（3）仿真得到的最大雷諾數遠小于通常認定的臨界雷諾數，表明微泵流體具有層流特性。

（4）泵腔內流體動態特性與泵膜的運動存在著密切關系，如果忽略了流固耦合效應，簡單地將微泵的驅動器與腔內的流場分離處理，必然歪曲了泵流體場的動態特性。泵膜變形、流體壓力和進出口流速等響應與輸入電壓信號之間存在著滯后現象。對微泵的3D全耦合仿真，能夠獲得驅動電信號與流體流量、泵送壓力等輸出變量之間的直接關系，有利于從整體意義上實現微泵的優化設計。

［1］Morris C J，Forster F K.Low－order Modeling of Resonance for Fixed－valve Micropumps Based on First Principles［J］.Journal Microelectromech.Syst.，2003，12：325－334.

［2］Olsson A，Stemme G，Stemme E.A Numerical Design Study of the Valveless Diffuser Pump Using a Lumped－mass Model［J］.Journal Micromech.Microeng.，1999，9：34－44.

［3］Bourouina T，Grandchamp J P.Modeling Micropumps with Electrical Equivalent Networks［J］.Journal Micromech.Microeng.，1996，6：398－404.

［4］Lin X Z，Ying J，Chen Zichen.Research on Terminal Behavior of Electrostatically Actuated Micropump Membrane Based on Modal Analysis［C］／／Wei Y L，Chong K T，Takahashi T，et al.ICMIT 2005：Mechatronics，MEMS and Smart Materials，SPIE.Bellingham，2005，6040：P60400U.

［5］Faris W F，Abdel－Rahman E M，Nayfeh A H.Mechanical Behavior of an Electrostatically Actuated Micropump［C］／／Agnes G，Chamis C，Noor A，et al.43rd AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference.Denver，2002：AIAA2002－1303.

［6］Morris C J，Forster F K .Optimization of a Circular Piezoelectric Bimorph for a Micropump Driver［J］.Journal Micromech.Microeng.，2000，10：65－459.

［7］王立文，高殿榮，楊林杰，等.壓電驅動微泵泵膜振動有限元分析［J］.機械工程學報，2006，42（4）：230－235.

［8］Ullman A，Fono I.The Piezoelectric Valve－less Pump—improved Dynamic Model［J］.Journal Microelectromech.Syst.，2002，11：655－664.

［9］Pan L S，Ng T Y，Wu X H，et al.Analysis of Valveless Micropumps with Inertial Effects［J］.Journal Micromech.Microeng.，2003，13：390－399.

［10］MacHauf A，Nemirovsky Y，Dinnar U.A Membrane Micropump Electrostatically Actuated Across the Working Fluid［J］.Journal Micromech.Microeng.，2005，15（12）：2309.

［11］白蘭，馮志慶，吳一輝.無閥微泵動態特性的固液耦合分析［J］.機械工程學報，2008，44（7）：69－74.

［12］謝海波，傅新，楊華勇.微型無閥泵流動特征仿真與試驗研究［J］.機械工程學報，2002，38（7）：54－57.

［13］楊愷祥.壓電無閥式微泵浦制造與測量分析［D］.臺灣云林縣：臺灣云林科技大學，2004.

［14］Tsui Y Y，Lu S L.Evaluation of the Performance of a Valveless Micropump by CFD and Lumpedsystem Analyses［J］.Sensors and Actuators A：Physical，2008，148（1）：138.

［15］Yao Q，Xu D，Pan L S，et al.CFD Simulation of Flows in Valveless Micropumps［J］.Eng.Appl.Comput.Fluid Mech.，2007，1（3）：181－188.

［16］林謝昭，應濟，陳子辰.靜電無閥微泵兩種仿真模型的比較研究［J］.哈爾濱工業大學學報，2010，42（12）：1943－1947.