區間不確定系統迭代學習控制的單調收斂性

李宏勝 劉 娣 滕福林 黃家才 張建華

南京工程學院，南京，211167

0 引言

許多運動控制系統需進行沿某軌跡的重復運動，例如數控機床沿一定的軌跡重復加工零件，機械手重復執行某一運動過程。通常的控制算法并未考慮此類運動的重復特性，每一次運行跟隨誤差都重復產生，跟蹤精度不高。而且由于控制對象存在非線性因素且模型具有不確定性，因而使得設計高性能的常規控制器較為困難。迭代學習控制是一種較新的智能控制方法，它首先由Arimoto［1］提出并應用于機械手的控制中。近年來迭代學習控制理論體系越來越成熟［2］，應用日益廣泛。

迭代學習控制的基本思想是，通過學習每次運動的誤差，對控制量進行前饋修正，從而在下次運動時提高運動的精度。它不需要精確的系統模型，對系統的未建模特性具有一定的魯棒性，實時計算量小，在一定的條件下可保證迭代收斂。迭代學習控制通常要求運動軌跡、初始條件和系統特性具有重復性，并要有足夠的存儲器來存儲上次運動控制的信息［3－4］。

概率方法、模糊方法和區間方法是目前不確定性建模的三種主要方法。概率方法和模糊方法均需要有足夠的數據來分別確定不確定結構參數的概率密度或隸屬度函數，區間方法是把這些不確定性結構參數視為未知變量，并在具有已知邊界的區間內取值。參數區間不確定性迭代學習控制系統收斂性的研究主要集中在穩定性（asymptotic stability）和單調收斂性（monotonic convergence）上。本文討論了參數區間不確定性迭代學習控制系統（IILC）的單調收斂性問題。

1 迭代學習控制的單調收斂性

z傳遞函數描述的離散線性時不變系統為

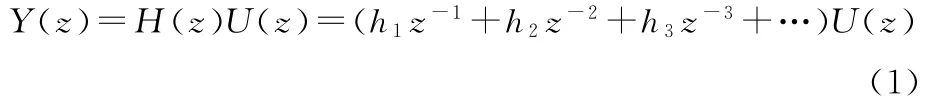
其中，hi為H（z）的Markov參數，理想輸出信號為yd（t），第k次迭代學習控制的輸入、輸出分別為uk（t）、yk（t），ek（t）＝yd（t）－yk（t），t為離散時間變量，t∈ ［0，N］。

定義超向量（Supervectors）［5-9］：

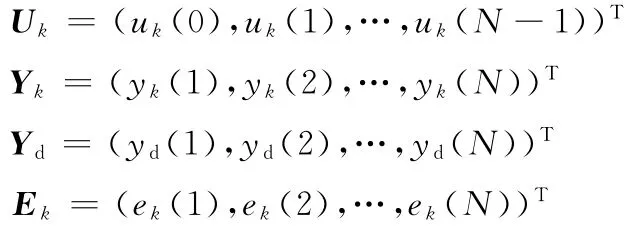
則Yk＝HpUk，其中Hp為由系統Markov參數組成的N×N矩陣：

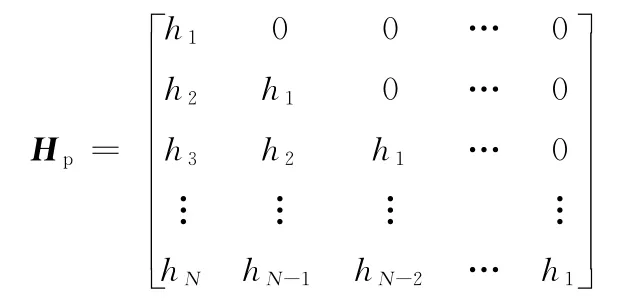
迭代ILC算法的目標是根據第k次及以前的信息計算出第k＋1次的控制輸入uk＋1，使其收斂至u＊（t），并使得ek（t）＝yd（t）－yk（t）收斂到零。超向量法（supervector）將二維（時間軸、迭代軸）問題轉換為一維多輸入多輸出問題。超向量表達的一般迭代學習控制為

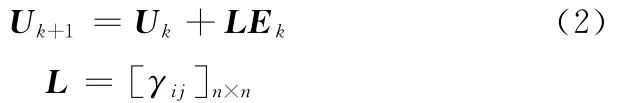
上述學習矩陣L的不同選擇方法對應不同的ILC學習算法，顯然，當γij＝0（i≠j）、γij＝γ（i＝j）時為Arimoto算法。

定義T為列向量h＝（h1，h2，…，hN）T到下三角陣Hp的Toeplitz變換，即Hp＝T（h）。

設l＝［k1，k2，…，km，0，0，…，0］T∈RN×1，m為ILC算法的階次，取L＝T（l）為ILC算法學習矩陣。

考慮離散高階ILC算法（式（2）），則

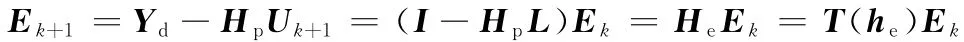
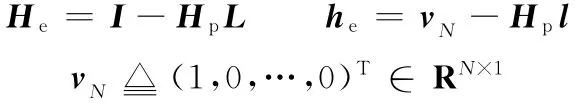
因此，ILC單調收斂的充分必要條件為相應的范數小于1，即

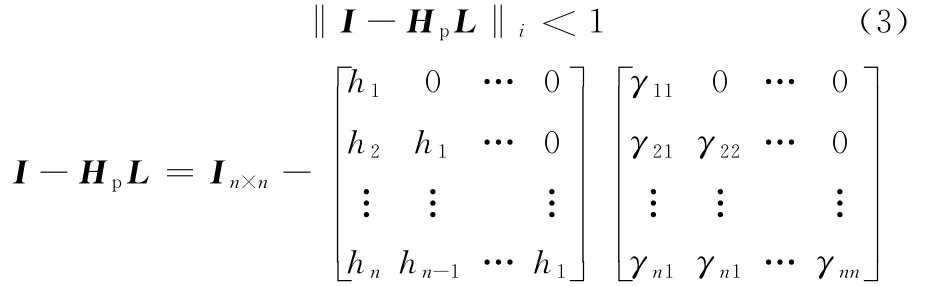
2 區間魯棒迭代學習控制的單調收斂性

對于區間矩陣集合：

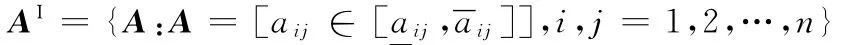
其頂點矩陣集合：

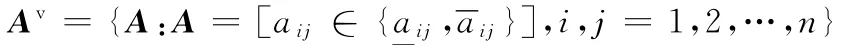
對區間魯棒迭代學習控制系統穩定性和單調收斂性的討論即為對給定的HIp進行討論。顯然，對Arimoto型迭代學習控制，穩定性的充要條件為

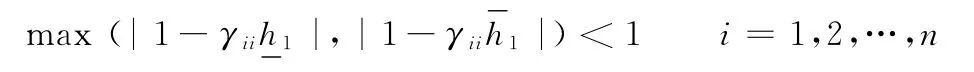
對一般區間魯棒迭代學習控制，設P＝I－Hp?L，則其穩定性的充要條件為PI＝I－HIp?L的譜半徑小于1。而區間矩陣PI＝I－HIp?L的譜半徑為P∈Pv的某個譜半徑。

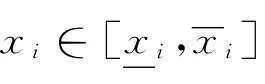
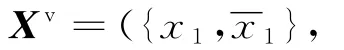
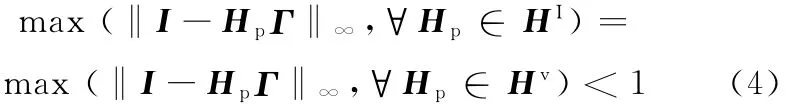
時區間魯棒迭代學習控制系統l∞范數意義單調收斂，其中，Hv為Markov頂點矩陣。對離散高階ILC算法（式（2）），PD型ILC算法（m＝2）為［6］

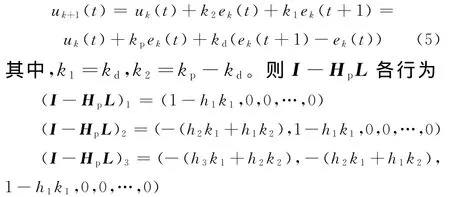
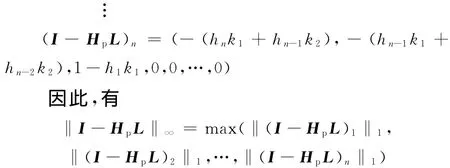
3 數字仿真研究

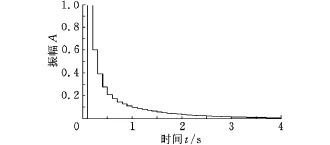
圖1 系統脈沖傳遞函數（a＝0.80）

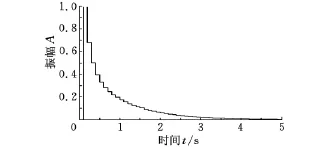
圖2 系統脈沖傳遞函數（a＝0.72）

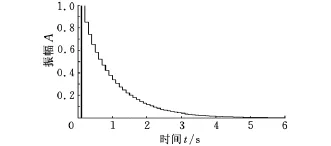
圖3 系統脈沖傳遞函數（a＝0.55）

對上述區間不確定系統a ∈ ［0.55，0.80］，采用式（5）離散二階ILC算法：

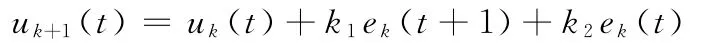
（1）選取控制參數k1＝0.90、k2＝－0.59［6］，當a＝0.80（上界）時，‖I－HpL‖∞＝0.28＜1，其輸出軌跡及軌跡誤差范數如圖4、圖5所示。可見，迭代學習控制取得了良好的單調收斂性能。當a＝0.72時，‖I－HpL‖∞＝0.46＜1，其軌跡誤差范數如圖6所示。 當a＝0.55（下界）時，‖I－HpL‖∞＝1.07＞1，其軌跡誤差范數如圖7所示。可見，當參數區間變化至下界時，不滿足式（4）條件，迭代學習控制不滿足單調收斂的要求。

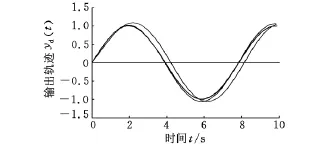
圖4 隨迭代次數增加，系統輸出曲線

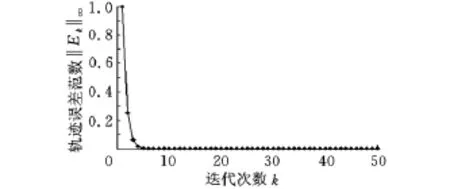
圖5 隨迭代次數增加，誤差范數的變化

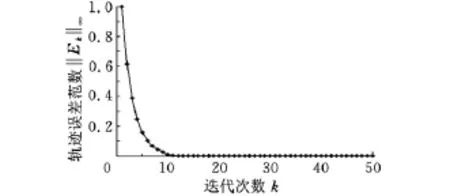
圖6 隨迭代次數增加，誤差范數的變化

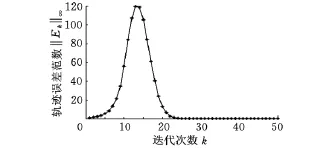
圖7 隨迭代次數增加，誤差范數的變化

（2）選 取k1＝0.80、k2＝－0.59，當a ＝0.80（上界）時，‖I－HpL‖∞＝0.41＜1，其輸出軌跡及軌跡誤差范數如圖8、圖9所示。當a＝0.72，‖I－HpL‖∞＝0.34＜1，其輸出軌跡及軌跡誤差范數如圖10所示。當a＝0.55（下界）時，‖I－HpL‖∞＝0.746＜1，其軌跡誤差范數如圖11所示。可見，當參數取上下界時，均滿足式（4）條件，迭代學習控制滿足區間單調收斂的要求。

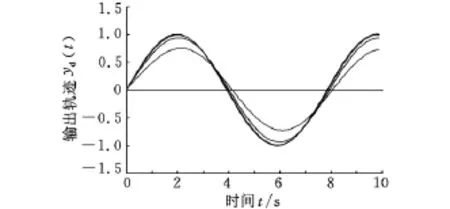
圖8 隨迭代次數增加，系統輸出曲線

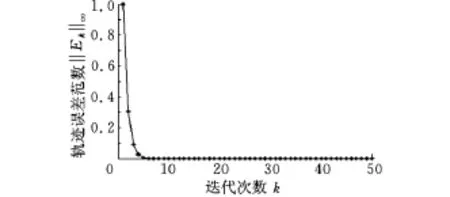
圖9 隨迭代次數增加，誤差范數的變化

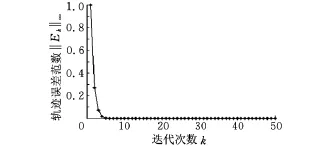
圖10 隨迭代次數增加，系統輸出曲線

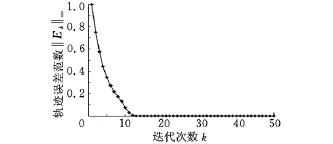
圖11 隨迭代次數增加，誤差范數的變化

4 結語

本文研究了區間不確定離散線性時不變系統的魯棒迭代學習控制（IILC）算法的單調收斂性，并針對常見的離散PD型ILC算法，給出了在l∞范數意義下區間不確定性迭代學習控制系統單調收斂性的判斷方法。仿真實例說明，當Markov參數組成的頂點矩陣滿足單調收斂性條件時，區間不確定系統的迭代學習控制具有魯棒單調收斂性。

［1］Arimoto S，Kawamura S，Miyazaki F.Bettering Operation of Robots by Learning［J］.Journal of Robotic Systems，1984，1（2）：123－140.

［2］Moore K L，Xu Jianxin.Special Issue on Iterative Learning Control［J］.Int.J.Control，2000，73（10）：819－823.

［3］Moore K L.An Observation about Monotonic Convergence in Discrete－time，P－type Iterative Learning Control［C］／／Proceedings of IEEE Int.Symposium on Intelligent Control（ISIC’01）.Mexico，2001：45－49.

［4］許順孝，揚富文.不確定線性系統迭代學習控制器的設計［J］.控制理論與應用，2002，19（4）：650－652.

［5］Chen Yangquan，Moore K L.An Optimal Design of PD－type Iterative Learning Control with Monotonic Convergence［C］／／Proceedings of the 2002IEEE International Symposium on Intelligent Control.Vancouver，Canada，2002：27－30.

［6］李宏勝.離散系統單調收斂高階迭代學習控制［J］.機械工程學報，2006，42（6）：72－76.

［7］Moore K L，Chen Yangquan.On Monotonic Convergence of High Order Iterative Learning Update Laws［C］／／2002IFAC 15th Triennial World Congress.Barcelona，Spain，2002：21－26.

［8］Moore K L，Chen Yangquan.A Separative Highorder Framework for Monotonic Convergent Iterative Learning Controller Design［C］／／Proceedings of the American Control Conference.Denver，Colorado，USA，2003：3644－3649.

［9］Moore K L.Multi－loop Control Approach to Designing Iterative Learning Controllers［C］／／Proceedings of the 37th IEEE Conference on Decision＆Control.Tampa，Florida，USA，1998：666－671.