基于連續潮流的靜態分岔點追蹤方法

李林劉玲

(德陽電業局變電檢修中心，四川德陽 618000)

電力市場化改革以后，經濟的快速增長，投入系統的設備增長迅猛，同時電力網絡的發展相對滯后，很多地方的電網都經常運行在極限狀態，可能遭受電壓穩定的威脅［1］。靜態電壓穩定分析能判斷電力系統有多大的靜態電壓穩定裕度并指出采取何種合適的控制措施使電力系統運行在安全裕度之內［2］。

在電力系統靜態電壓穩定性分析中，電壓崩潰點是與靜態分岔點相聯系的。電力系統中主要有兩種靜態分岔點:鞍結分岔點(saddle－node bifurcation point，SNBP)和極限誘導分岔點(limit－induced bifurcation point，LIBP)。前者對應潮流雅可比矩陣的奇異點;后者則是由于某發電機節點的無功出力達到極限而導致系統穩定平衡點忽然消失［3］。因此，只有準確搜索和識別這兩類分岔點，才能準確地計算系統的電壓穩定裕度，進而準確地計算在該分岔點處各種控制變量對于穩定裕度的靈敏度信息，從而進行預防控制［4］。求取電壓靜態分岔點的算法主要有連續潮流法［5－7］、崩潰點直接計算法［8－10］、最優潮流計算法［11－13］。

文獻［4］利用連續潮流法和崩潰點法的混合方法對極限誘導分岔點和鞍結分岔點進行了識別和計算。文獻［14］利用預測－校正方法快速穿越電壓崩潰臨界點的方法來搜索。文獻［15］采用觸發條件和兩個檢測條件的判斷準則，對結構變化點進行檢測，從而判斷極限誘導分岔點的存在。這3篇文獻中都提到利用最優步長的方法來計算，但是都沒有告訴具體的方法。這里采用發電機無功極限值引導變步長的連續潮流法來搜索靜態分岔點，繼而利用雅可比矩陣特征值的符號變化進行識別。該方法應用于IEEE 39節點測試系統，顯示了該方法的正確性和有效性。

1 連續潮流的數學模型

一般，在靜態輸電計算中，極坐標系統下的潮流方程可用式(1)表示為

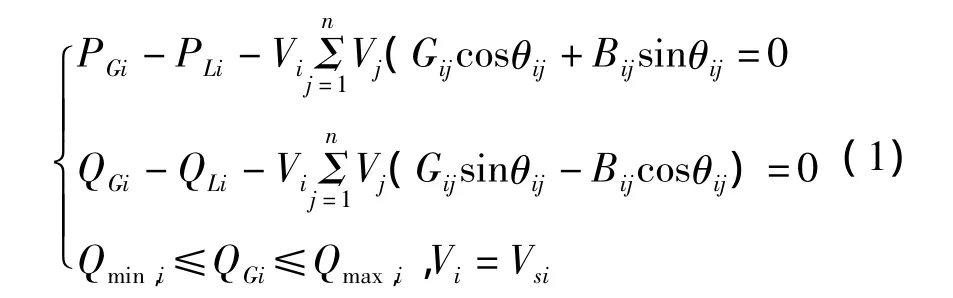
式中，PGi、QGi為節點 i的發電機有功和無功出力;Qmin，i、Qmax，i為發電機的最小和最大無功極限值;PLi、QLi為節點i負荷的有功和無功;Vi、Vsi是節點i的電壓幅值和節點i的標準電壓幅值;θij是節點i和節點j的電壓相角差值;Gij、Bij為節點i與節點j之間的網絡導納矩陣的實部和虛部。

若用λ表示發電機和負荷的增長參數，即為負荷因子;nGi、nPLi分別表示發電機和負荷有功增長的方向向量;nQLi表示負荷無功增長的方向向量。則有

由于引入變量λ，使潮流方程的未知數比方程數多一個，為了使未知數的個數和方程數相同，避免潮流雅可比矩陣奇異，此時需要增加一維參數化方程。

連續潮流主要由4部分組成:預估、校正、參數化和步長控制。具體步驟不再敘述，詳情請參考文獻［16］、［17］。

2 發電機無功受限后現象分析

在實際潮流計算中，發電機的無功并不是不變的。當發電機的無功始終維持在最小值與最大值之間范圍內時，潮流雅可比矩陣在最大功率傳輸點奇異，其靜態分岔類型為鞍結分岔(saddle－node bifurcation，SNB);當發電機的無功越限時，系統中PV節點的無功功率達到極限將保持不變，而節點電壓發生跌落現象，在潮流方程中發電機節點由PV節點類型轉化為PQ節點類型，潮流方程中QGi取值如下。

若 QGi≤ Qmin，i時，QGi=Qmin，i，Vi≤Vsi若 QGi≥ Qmax，i時，QGi=Qmax，i，Vi≤Vsi

此時，系統可能發生兩種現象:無功/電壓約束轉換(constraint exchange pomt，CEP)和極限誘導分岔(Gmit－induead bifurcation，LIB)。

2.1 無功/電壓約束轉換

CEP對應的分岔圖如圖1所示。圖中，點A為系統初始運行點，此時發電機無功沒有越限。隨著負荷的增加，當發電機無功達到極限(B點)時，系統的結構發生突然變化，運行點從QGi≤QGmaxi曲線的上半分支轉化到Q=QGmaxi曲線的上半分支運行，此時系統是穩定的。如果再增加負荷，系統將運行到C點，就會發生SNB而導致電壓崩潰。對于B點來講，是一個

圖1 無功/電壓約束轉換

2.2 極限誘導分岔

LIB對應的分岔圖如圖2所示。圖中，點A為系統初始運行點，此時發電機無功沒有越限。隨著系統負荷的增加，當發電機無功達到極限(B點)時，運行點突然從QGi≤QGmaxi曲線的上半分支轉化到QGi=QGmaxi曲線的下半分支運行，形成一個不同于C點(SNBP)的尖點形狀，系統的結構突然改變導致了電壓崩潰。對于B點來講，是一個不穩定的運行點，這就是LIBP。

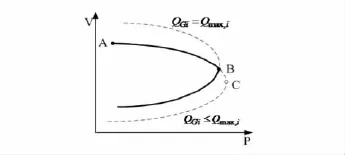
圖2 極限誘導分岔

3 靜態分岔點的追蹤

3.1 靜態分岔點的搜索

搜索方法通常用常規連續潮流法，從起始點開始逐個搜索。這樣的話，一方面降低了算法的效率，另一方面，如果連續潮流法的步長過大的話，多臺發電機都穿越了分岔點。因此，要用盡可能少的步數達到和穿越分岔點，從而可以把分岔點限制在一個較小的范圍內，為精確識別做好準備。

于是采用發電機無功極限值引導變步長連續潮流法來搜索分岔點。當發電機無功沒有越限時，采用較大步長的非線性預估，當發電機快要達到無功極限時，采用較小的步長，避免多臺發電機在相鄰短時間內先后越限。具體步長控制策略如下。

式(1)中發電機的無功功率QGi可以如下描述。

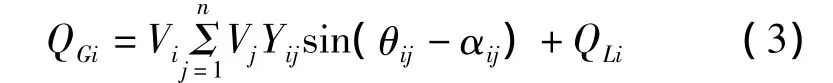
式中，Yij和αij是導納矩陣在極坐標下的元素。對于一個特定的電力系統，導納矩陣是一定的，所以Yij和αij是個常數。對于發電機節點來說Vi也是個常數，如果電力系統在正常條件下運行，相角差θij通常很小，所以，式(3)中的正弦函數接近于常數，描述如下。

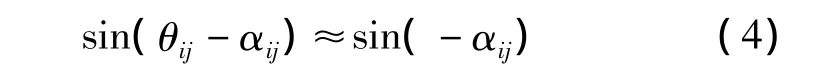
從式(3)中可以看出電壓幅值Vj是唯一的變量，即發電機的無功功率QGi是關于電壓幅值Vj的函數，這樣可以簡化式(3)如下。

式中，K=［k1，k2，k3，…kn］是線性系數矩陣，V=［V1，V2，V3，…Vn］T是系統的電壓幅值矩陣。從式(5)可以看出Vi與QGi成線性關系。負荷因子λ與電壓幅值Vi接近于平方關系［18］，所以負荷因子λ與發電機的無功功率QGi也接近于平方關系。關系示意圖如圖3所示，表達式描述如下。

圖3 負荷因子λ與發電機無功QGi的關系

如果知道式(6)的3個解，根據二階拉格朗日插值就可以得出系數ai、bi和ci。當發電機的無功到達極限，把上限QGimax和下限QGimin代入式(6)，可以得到發電機無功越限時相應的負荷因子。

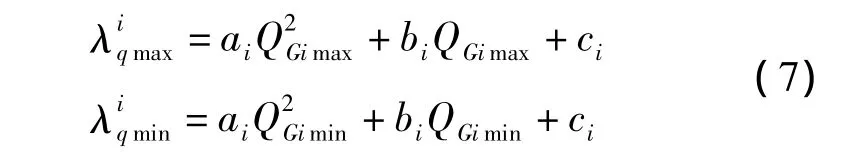
3.2 靜態分岔點的識別

分岔點可根據靜態分岔類型的特點進行識別。SNB的特點是，雅可比矩陣有零特征值出現;CEP的特點是，在無功/電壓約束轉換過程的前后，雅可比矩陣的所有特征值仍在左開半平面;LIB的特點是，在發生分岔之前，雅可比矩陣的所有特征值仍在左開半平面，而在發生分岔之后，雅可比矩陣的最小特征值跳躍到右開半平面。

3.3 追蹤分岔點的步驟

1)采用連續潮流法計算出3個運行點，獲得λ與QGi值;

2)利用二階拉格朗日插值法獲取式(6)的系數ai、bi和 ci;

3)利用式(7)計算出發電機無功越限后的λq值，從而計算出連續潮流的步長h;

4)利用連續潮流法進行預估、校正，得到潮流解;

5)對潮流解進行識別，若不是分岔點就采用固定小步長進行搜索，執行上一步;若是分岔點則搜索成功，把PV節點轉化為PQ節點，執行第二步，進行下一個點的搜索。

4 算例分析

下面以IEEE 39節點測試系統對采用的方法進行了驗證。仿真中所有的負荷和發電機的有功按同一比例λ增長，負荷為恒功率模型，并且保持功率因數不變。發電機無功功率取值范圍如表1所示，其中Bus_38發電機的最大無功功率Qmax有兩個值，對應兩種不同的模式。

表1 發電機無功功率取值范圍

模式1:Bus_38的 Qmax=1.5。Bus_6的 PV曲線如圖4所示。隨著負荷因子的增加，系統的初始運行曲線為曲線1，某一發電機到達無功受限點A后，系統的潮流方程發生了突變，運行曲線變化到曲線2。接著發電機無功受限點依次為B、C、D，運行曲線對應依次變化為曲線3、4、5，隨著負荷因子的進一步增加，系統運行到E點，發生電壓崩潰。

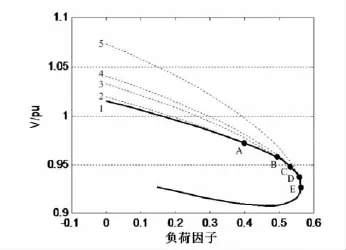
圖4 模式1下Bus_6的PV曲線圖

圖4中，A、B、C、D、E 對應的識別結果如表2所示。從表中可以看出在受限點A、B、C、D潮流雅可比矩陣特征值符號都是從負變化到負，即潮流雅可比矩陣的所有特征值仍在左開半平面，系統仍然穩定。在受限點E負荷達到最大，潮流雅可比矩陣特征值從符號為負變化為零，此時對應電壓穩定臨界點。所以模式1下的電壓崩潰是由于鞍結分岔所致。

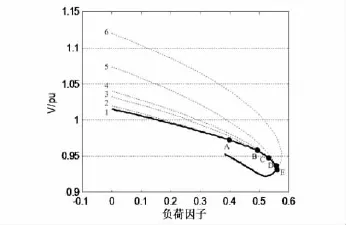
圖5 模式2下Bus_6的PV曲線圖

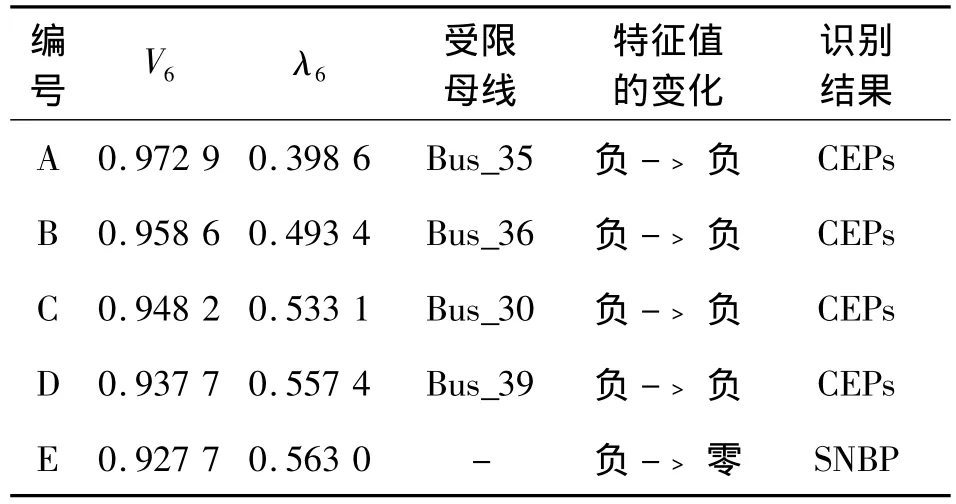
表2 模式1下測試系統的識別結果

模式2:Bus_38的Qmax=0.32。Bus_6的PV曲線如圖5所示。隨著負荷因子的增加，發電機的無功功率受限點依次為A、B、C、D、E，各點對應的識別結果如表3所示。

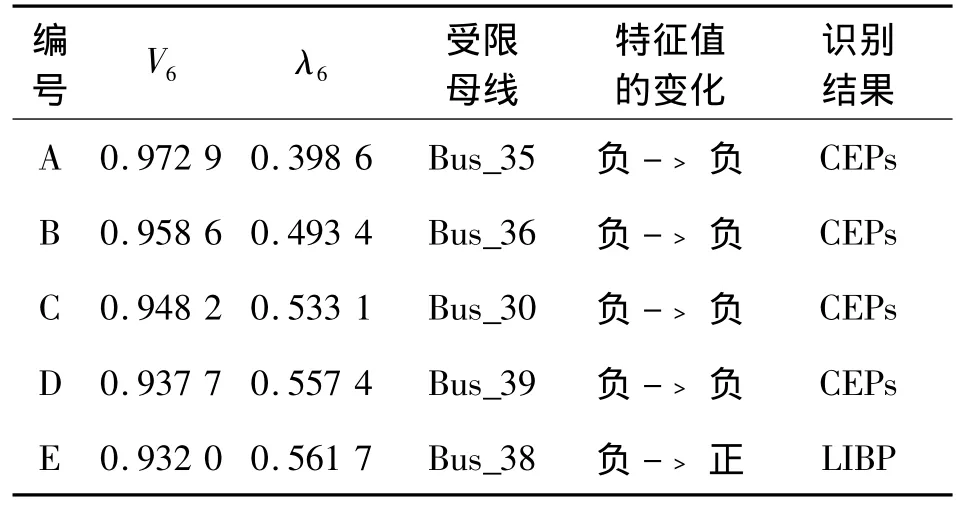
表3 模式2下測試系統的識別結果

從圖5和表3可以看出在受限點A、B、C、D潮流雅可比矩陣特征值符號都是從負變化到負，即潮流雅可比矩陣的所有特征值仍在左開半平面，系統仍然穩定。在受限點E負荷達到最大，潮流雅可比矩陣特征值符號從負變化到正，即在發生分岔之前，潮流雅可比矩陣的所有特征值仍在左開半平面，而在發生分岔之后，潮流雅可比矩陣的特征值跳躍到右開半平面，此時發生電壓崩潰。所以模式2下的電壓崩潰是由于極限誘導分岔所致。

5 結論

對發電機無功受限后出現的無功/電壓約束轉換和極限誘導分岔現象進行了分析，并采用了發電機無功極限值引導變步長的連續潮流法，對靜態電壓穩定分析中兩類主要的分岔點進行了搜索，繼而利用潮流雅可比矩陣特征值的符號變化進行識別。通過IEEE 39節點測試系統的算例分析，取得了理想的效果，表明了該方法的正確性和有效性。本方法可以提供系統可能的電壓崩潰方式，這對電力系統運行人員進行預防控制具有非常重要的指導意義。

［1］王冰，游振華，韓學軍，等.考慮負荷靜態電壓特性的重負荷節點靜態電壓穩定分析［J］.繼電器，2007，35(11):21－25.

［2］李娟，陳繼軍，司雙.連續潮流與免疫遺傳算法結合的靜態電壓穩定裕度計算［J］.電力系統保護與控制，2010，38(18):24 －27.

［3］Canizares C.A.，Mithulananthan N.，Berizzi A.，et al.On the Linear Profile of Indices for the Prediction of Saddle－node and Limit－induced Bifurcation Points in Power Systems［J］.IEEE Trans on Circuits and Systems I:Fundamental Theory and Applications，2003，50(12):1588－1595.

［4］馬冠雄，劉明波，王奇.一種識別靜態電壓穩定分岔點的混合方法［J］.電力系統自動化，2006，30(24):17 －20.

［5］Ajjarapu V.，Christy C.The Continuation Power Flow:A Tool for Steady State Voltage Stability Analysis［J］.IEEE Transactions on Power Systems，1992，7(1):416 –423.

［6］Feng Z.，Ajjarapu V.，Long B..Identification of Voltage Collapse Through Direct Equilibrium Tracing［J］.IEEE Transactions on Power Systems，2000，15(1):342 －349.

［7］Yorino N.，LI Huaqiang，，Sasaki H..A Predictor/corrector Scheme for Obtaining Q－limit Points for Power Flow Studies［J］.IEEE Trans on Power Systems，2005，20(1):130－137.

［8］Canizares C.A.，Alvarado F.L..Point of Collapse and Continuation Methods forLlarge AC/DC Systems［J］.IEEE Trans on Power Systems，1993，8(1):1 －8.

［9］郭瑞鵬，韓禎祥.電壓崩潰臨界點計算的改進零特征根法［J］.中國電機工程學報，2000，20(5):63－66.

［10］Rosehart W.D.，Canizares C.A.，Quintana V.H.Multiob jectiveOptimal Power Flows to Evaluate Voltage Security Cost in Power Networks［J］.IEEE Trans on Power Systems，2003，18(2):578 －587.

［11］Irisarri G.D.，Wang X.，Tong J.，et al.Maximum Load A-bility of Power Systems Using Interior Point Non－linear Optimization Method［J］.IEEE Trans on Power Systems，1997，12(1):162 －172.

［12］韋化，丁曉鶯.基于現代內點理論的電壓穩定臨界點算法［J］.中國電機工程學報，2002，22(3):27－31.

［13］李華強，劉亞梅，YORINO N.鞍結分岔與極限誘導分岔的電壓穩定性評估［J］.中國電機工程學報，2005，25(24):56－60.

［14］趙晉泉，江曉東，張伯明.一種靜態電壓穩定臨界點的識別和計算方法［J］.電力系統自動化，2004，28(23):28－32.

［15］熊寧，程浩忠，馬則良，等.基于連續潮流的極限誘導分岔檢測方法［J］.電力系統自動化，2008，32(18):35－38.

［16］徐曉春，萬秋蘭，顧偉，等.在線電壓穩定分析中快速連續潮流的應用［J］.電力系統保護與控制，2008，36(14):37－41.

［17］周雙喜，朱凌志，郭錫玖，等.電力系統電壓穩定性及其控制［M］.北京:中國電力出版社，2004.

［18］Antonio C.Z.de Souza，Claudio A.Canizzares，Victor H.Quintana.New Techniques to Speed up Voltage Collapse Computations Using Tangent Vectors［J］.IEEE Trans on Power Systems，1997，12(3):1380 – 1387.