對稱耦合雙振子的復雜運動

張建國，張玉芬

（1.寧夏師范學院教育技術中心，寧夏固原 756000；2.河北大學數學與計算機學院，河北保定 071002）

對稱耦合雙振子的復雜運動

張建國1，張玉芬2

（1.寧夏師范學院教育技術中心，寧夏固原 756000；2.河北大學數學與計算機學院，河北保定 071002）

建立了一個雙彈簧對稱耦合的振子系統.計算了通過升維降階技術得到的一個等價系統的Lyapunov指數，表明振子的運動或為混沌或為準周期.振子中沒有引入能量耗散，其運動軌跡因初始條件不同而有很大不同.最后指出，判斷這樣的系統性態，唯一可靠的方法是計算Lyapunov指數.

耦合振子；Lyapunov指數；運動軌跡；系統性態

彈性振子作為一種極其簡單的物理模型，能夠展示非常豐富的非線性動力學行為［1－3］，長期以來備受關注.將多個振子耦合在一起，往往能夠展示許多物理系統的行為特征，如一個平面上的耦合振子陣列能夠模擬表面聲波在金屬材料中的傳播［4－5］，多振子耦合模型能夠模擬非剛性分子的振動［6］等等.由于耦合振子具有各式各樣的物理背景，對相關模型基本特征進行研究不僅是必要的，而且對理解相關物理系統的特性及其機制是至關重要的.本文建立一個對稱雙振子模型，通過拉格朗日函數獲得其運動方程，數值求解方程獲得振子的運動軌跡.結果表明振子的運動強烈依賴于初值，表現在振子運動軌跡因初值不同而不同，且在相空間中做遍歷運動.這是因為所考察的振子系統無耗散因素存在，因而是保守系統中典型的非線性動力學行為.Lyapunov指數（exponent）表明所關注的參數組合下系統的運動或為混沌運動或為準周期運動.

必須指出，此前的研究者多不關注耦合振子的運動性態，其研究僅停留在對振子軌跡的描述上.得到的這個結果將提醒相關研究者，當不存在耗散因素時耦合振子系統是一個保守的非線性動力學系統，這樣的系統有其固有的動力學特征.另外，一些看似周期的運動實際可能是遍歷運動，而遍歷運動往往是混沌或準周期的.這種運動單憑肉眼觀察振動曲線是無法與周期運動相區別的.

1 對稱耦合雙振子模型

對稱雙彈性振子物理模型可以用一個在光滑水平面上運動的質量為m的質點來描述，它與2個彈性系數均為k，原長均為a的彈簧相連.這里，光滑意味著忽略能量耗散，是一個理想體系.平衡時這2個彈簧成一條直線，此時彈簧原長為a，質點在水平的xoy平面內作微小振動.為簡單起見，質點平衡位置取在原點o處.模型由圖1表示.

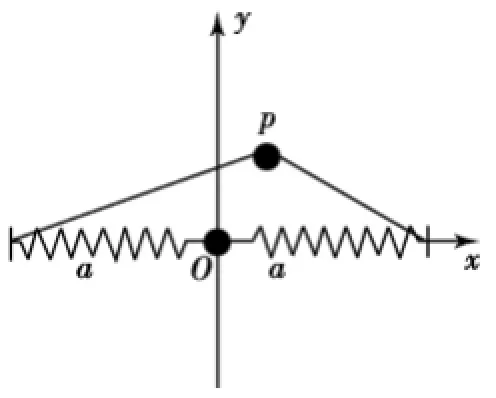
圖1 雙彈性振子模型Fig.1 Double esastic oscillator model

以下將解析獲得系統的運動方程.容易給出此系統的動能和勢能，分別是

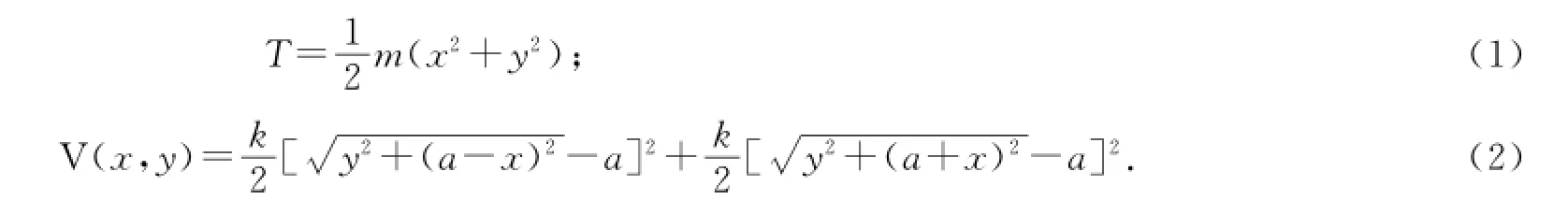
系統的拉格朗日函數可寫為

顯然，方程（10）和（11）是一組非線性耦合方程.表明線性彈性振子通過相互耦合將轉變為非線性振動，體現了簡單單元耦合導致新特征涌現的普遍機制.眾所周知，這樣的非線性方程組很難直接解析求解，將借助于軟件Mathematica數值求解.

2 李雅普諾夫指數譜

為了便于計算Lyapunov指數以確定耦合振子運動性態，將通過升維降階的辦法將方程組（10）和（11）化為一階方程組

這里彈性振子質量m＝1 kg，彈簧原長a＝1.0 m，設彈性系數為控制參量.圖2給出系統的Lyapunov指數（Exponent）譜.譜線顯示k＜0.074參數范圍，絕大多數參數區至少有1個指數大于0，表明振子的運動是混沌的，而在k＞0.074參數范圍4個指數值在0附近振蕩，表明振子的運動是準周期的或在個別小區域是周期的.

圖2 耦合振子模型的Lyapunov指數譜Fig.2 Lyapunov exponent spectrum of the couplled oscillator mode

3 混沌運動

作為一個例子，挑選混沌區的一個參數k＝0.07，取初始條件為x0＝0.25 m，y0＝0.88 m，x·0＝0.009 m／s，y·0＝0.1 m／s，將對應振子的軌跡顯示于圖3.顯然，振子在一個區域之中做遍歷運動.由于模型沒有考慮能量耗散，因此是一個典型的保守系統.沒有耗散性的系統就沒有吸引性，因此振子的軌跡均因初態不同而不同，可以說“是一點一線”，意思是一個初態對應一條絕不同于另一初態下的軌跡.明確了混沌和準周期參數區之后，有必要將模型還原為方程組（10），（11）.當然，非常容易理解，方程組（12）－（15）的解在yx平面的投影確信無疑就是原方程組的解.

圖3 方程組（12）—（15）的解Fig.3 Solutions of equations（12）—（15）

為了使讀者獲得保守振子“一點一線”的直觀映像，獲得對這類沒有瞬態的動力學的理解，圖4給出k＝0.07時3組不同初態下的運動軌跡.其中圖a為x0＝0.25 m，y0＝0.88 m，x·0＝0.009 m／s，y·0＝0.1 m／s；圖b為x0＝0.4 m，y0＝0.25 m，x·0＝0.001 m／s，y·0＝0.09 m／s；圖c為x0＝0.4 m，y0＝0.25 m，x·0＝0.001 m／s，y·0＝0.001 m／s.結果顯示了運動軌跡對初始條件的強烈依賴.

圖4 不同初態下振子的混沌軌跡Fig.4 Chaotic trajectories in different initial conditions

4 準周期運動

非線性保守系統“一點一線”的運動特征對準周期運動也不例外.圖5給出準周期參數中k＝0.1時3組不同初始條件下振子的準周期運動軌跡，其中圖a為

結果表明，振子的準周期混沌運動一樣是遍歷運動，而且運動軌跡與初態一一對應.但是，單從振子的運動軌跡看，無法區分混沌運動與準周期運動.唯一可靠的辦法是計算系統的Lyapunov指數.另外一個必須注意的問題是此前一些單從振動圖線做出粗略判斷，認為系統做周期運動的作法不妥，往往導致錯誤認識，因為耦合振子是強非線性系統，混沌的和準周期的遍歷運動遠比封閉軌道的周期運動普遍.在不引入耗散的情況下，“一點一線”的保守系統特性，使系統運動的復雜性增加了，同時也增加了認識系統性態的難度.

圖5 不同初態下振子的準周期軌跡Fig.5 Quai－periodic trajectories in different initial conditions

5 結束語

模擬研究了對稱耦合雙振子系統的平面運動，由Lyapunov指數判斷這個系統既有混沌運動又有準周期運動，當然不排斥一些參數區存在周期運動.由于所考察的系統是一個典型的保守非線性系統，所以即使準周期運動，其運動軌跡強烈依賴于初始條件.周期運動情形與此類似.因此，這樣的系統能夠展示非常豐富且復雜的運動形態.但必須指出，不借助于Lyapunov指數而單憑對運動軌跡或振動圖線的直接觀察對系統性態做出判斷的作法不妥，往往導致錯誤認識.

［1］楊正波，夏清華，劉思平.多彈簧振子耦合系統研究［J］.大學物理，2010，29（4）：29－32.

YANG Zhengbo，XIA Qinghua，LIU Siping.Investigation on the motion in coupled system of spring oscillators［J］.Coolege Physics，2010，29（4）：29－32.

［2］商澤進，王忠民.形狀記憶合金彈簧振子強迫振動的分貧與混沌［J］.中國機械工程，2010，21（16）：1986－1991.

SHANG Zejin，WANG Zhongmin.Bifurcation and chaos of forced vibration for a shape memory alloy spring oscillator［J］.China Mechanical Engineering，2010，21（16）：1986－1991.

［3］王立明.對稱雙彈簧振子系統的橫振動的主共振與分岔［J］.齊齊哈爾大學學報：自然科學版，2010，26（1）：85－87.

WANG Liming.Primary resonance and bifurcation of the forced transverse oscillation in the symmetric two－springed oscillator［J］.Journal of Qiqihar University：Natural Science Edition，2010，26（1）：85－87.

［4］陳陶，原森，陸建，等.應用彈性振子模型模擬聲表現波在金屬材料中的傳播過程［J］.南京郵電學院學報，2005，25（5）：75－78.

CHEN Tao，YUAN Sen，LU Jian，et al.Numerical simulation of the surface acoustic wave propagaed on the plate surface by mass spring lattice mode［J］.Journal of Nanjing Institute of Posts and Telecommunications，2005，25（5）：75－78.

［5］HERBERT G.Classical mechanics［M］.2nd.Massachusetts：Addison Wesley Publishing Company，1980.

［6］劉裕琴，管立.關于耦合振子運動的研究［J］.工科物理，1999，9（3）：6－8.

LIU Yuqin，GUAN Li.A study of the motion of coupled vibrator system［J］.Engineering Physics，1999，9（3）：6－8.

Complex movement in 2－space of a doubly asymmetric coupled spring

ZHANG Jian－guo1，ZHANG Yu－fen2
（1.Education Technology Center，Ningxia Teachers University，Guyuan 756000，China；2.College of Mathematics and Computer Science，Hebei University，Baoding 071002，China）

A system formed by two springs coupled asymmetrically is suggested.The Lyapunov exponent is calculated in anquivalent system obtained by an increasing dimension and reducing order method.It indicates that the system is chaotic or quasi－periodic in the majority region of the controlled parameter，the elastic coefficient.The trajectories of system bear typical characteristics of a conservative system，that is，one trajectory corresponds uniquely to one set of initial conditions.It should be pointed out that the nature of such coupled oscillators can be revealed only by lyapunov exponent.

coupled oscillator；Lyapunov exponent；trajectory；nature of sy stem

O344

A

1000－1565（2012）02－0144－05

2011－09－12

河北省軟科學研究項目（IF2008000236）

張建國（1968－），男，寧夏固原人，寧夏師范學院副教授，主要從事教育技術與非線性科學動力學研究.E－mail：jiaoyujish＠163.com

王蘭英）