復合勢中的玻色-愛因斯坦凝聚孤子的操控*

宋昌盛， 黎 菁， 王 瑩， 李峰波， 涂顏帥， 宗豐德

(浙江師范大學非線性物理研究所，浙江金華 321004)

0 引言

1995年，Anderson研究小組［1］通過激光和蒸發(fā)冷卻技術將稀薄堿金屬蒸氣降到極低的溫度，從而在實驗上首次實現了玻色-愛因斯坦凝聚態(tài)(BECs)．這為原子的波動特性提供了新的證據，也為研究和使用這種宏觀量子系統(tǒng)提供了重要的工具．目前，對BECs的實驗和理論研究多數已把目標鎖定在開發(fā)、操控和揭示宏觀量子現象上，如相位相干［2］、物質波衍射［3］、物質波傳輸［4］、物質波格柵、脈沖物質波激光［5］和量子邏輯［6］等．隨著BECs實驗不斷取得新進展，在諸多宏觀量子現象中，物質波孤子囚禁操控方面受到了特別關注．一般而言，產生吸引和排斥的BECs可通過Feshbach共振有效地加以調控［7］．其實，通過外勢來囚禁操控BECs在實驗上也是可行的，因為外勢中的光晶格勢是由波矢為2π/λ、夾角為θ相交入射的兩激光束干涉疊加而成［8］．在實驗中，可通過調節(jié)兩激光束的夾角改變光晶格勢的空間周期，也可通過改變激光束初相位隨時間調制確定改變光晶格勢的極小值位置．因此，在BECs的研究過程中，怎樣通過調節(jié)外勢來操控凝聚體已成為一個很有價值的現實問題．

本文重點研究由光晶格勢和拋物勢組成復合勢中的BEC孤子囚禁操控動力學．筆者在此提出了一種處理上述復合勢中的BEC孤子動力學的拓展變分法，將控制系統(tǒng)的非線性偏微分方程降階為更為簡捷的以揭示振幅、啁啾、中心位置和中心頻率波動為特征的4個耦合的非線性微分方程，從而可以清楚地理解BEC孤子在復合勢中的囚禁操控動力學特征，這將為BEC系統(tǒng)在精確量子測量和量子信息處理等方面的實驗和應用提供了有力的理論參考．

1 BEC模型與變分動力學系統(tǒng)

在足夠低的溫度和平均場近似下，稀薄的玻色氣體可采用帶有外勢的三維Gross-Pitaevskii方程［9］描述，而在一維雪茄型模型下吸引的BEC波函數被描述為帶外勢的非線性Schr?dinger方程(NLS)［10］

式(1)中:u(x，t)是Hartree-Fock近似下的規(guī)范復數平均場變量［11］;外勢場V(x，t)是光晶格勢和拋物勢的復合勢，具體形式如下:

式(2)中:V0和V1分別是光晶格勢和拋物勢的強度;參數k是產生光晶格勢的入射激光波數;參量x是光晶格勢的最小值和拋物勢最小值之間的最小偏移量．

筆者拓展已被廣泛應用于哈密頓系統(tǒng)中的變分法，從而得到BEC的變分動力學系統(tǒng)．一維雪茄型BEC的控制方程(1)的拉格朗日密度［12］為

由于選用高斯函數與雙曲函數作為孤子試探解的區(qū)別非常小［13］，故筆者選取帶有啁啾項的試探解為

式(4)中:參量η，β，x0，ξ，φ分別代表振幅、啁啾、中心位置、中心頻率和絕對相位，它們都是時間t的函數;常數A的大小由實驗給定的被囚禁BEC原子總數目決定．將式(4)代入式(3)得到平均拉格朗日函變分動力學系統(tǒng)為:

需要指出的是，在上述推導過程中做了簡化處理k/η?1，使得exp［-k2/(2η2)］≈1，這樣就拓展了文獻［14］的結果，使得對BEC動力學系統(tǒng)穩(wěn)定性分析變得簡捷;另外，方程(5)～方程(8)分別反映了振幅、啁啾、中心位置和中心頻率的相互作用．正是引入了啁啾項，使我們能捕捉到驅使孤子的振幅-寬度波動的二次相位變化的信息，因此，它能高質量地揭示出BEC系統(tǒng)的動力學特征．

2 BEC孤子的動力學演化

處理BEC變分動力學系統(tǒng)式(5)～式(8)的耦合非線性微分方程組的基本思路是:先求出靜態(tài)解，然后再分析其穩(wěn)定性［15］．這里先令

就可得靜態(tài)解(η0，β0，x00，ξ0);然后，對求得的靜態(tài)解進行線性穩(wěn)定性分析［15］，得到特征方程為

求解特征方程(9)，得到4個特征值解

圖1 5個穩(wěn)定晶格勢槽V(x)對應外勢場與位置x之間的關系曲線

根據線性穩(wěn)定性分析理論［15］可知，若4個特征值都是純虛數，則對應的靜態(tài)解是穩(wěn)定的;若有一個特征值是實數，則對應的靜態(tài)解將顯現鞍形結構且是不4個特征值都是純虛數，靜態(tài)解是穩(wěn)定的;只能產生心位置x0的變化，余弦函數將出現周期性振蕩，使得特征值λ3和λ4在純虛數(靜態(tài)解是穩(wěn)定的)和純實數(靜態(tài)解是不穩(wěn)定的)之間轉換．正是這一情形才為實現多穩(wěn)定晶格勢槽囚禁BECs提供了可能．要個穩(wěn)定晶格勢槽所對應的極小值位置(從左至右)．

表1 5個穩(wěn)定晶格勢槽極小值與對應位置x之間的關系

為了證實拓展變分法對于描述復合勢中的BEC孤子動力學演化的充分性，筆者將對BEC變分動力學系統(tǒng)式(5)～式(8)的數值解與基本NLS方程的直接數值仿真進行比較，這里，筆者利用分步傅立葉變換直接數值仿真NLS方程［16］，監(jiān)控基本守恒量和孤子的能量，又利用自適應步長控制的Runge-Kutta方法數值求解BEC變分動力學系統(tǒng)式(5)～式(8)［15，17］．

考慮一般情形，選取圖1中的部分參數來討論BEC孤子的動力學行為．圖2展示了外勢場穩(wěn)定晶格勢槽中x0=3．74的BEC孤子動力學特性．從BEC變分動力學系統(tǒng)式(5)～式(8)的時序圖可以看出，由于啁啾的波動而導致了振幅的波動，使得BEC孤子的演化過程中出現了呼吸行為．同樣，中心位置的變化會直接影響到中心頻率的變化，這正好驗證了前面4個耦合方程中的式(5)和式(7)．由此可知，當初始位置放置在外勢場穩(wěn)定晶格勢槽中時，孤子的動力學演化過程保持穩(wěn)定．值得指出的是，BEC變分動力學系統(tǒng)式(5)～式(8)的數值解與BEC控制方程(1)的直接仿真結果完全符合．

圖2 初始位置放置在穩(wěn)定靜態(tài)解附近的BEC孤子動力學行為

3 BEC孤子的操控

接下來討論復合勢中的BEC孤子的操控．主要通過如引言所述的調制光晶格勢的2種方式來實現操控BECs．第1種方式是通過復合勢的“平移拖曳操控”，操控函數為

式(12)中:x1和x2分別是BEC孤子的初始位置和目標位置;t0和τ是操控參數，分別代表操控開啟時間和操控持續(xù)時間．整個拖曳過程是在絕熱情形下進行的，要求τ取較大的值(τ=10)．若τ很小，則整個操控過程就會完全失去對BEC孤子的引導作用，最后使得整個BEC崩塌．操控過程猶如一個機器手，在無形地平移拖曳著，使BEC孤子在操控時間范圍內成功地從初始位置移動到任意目標位置．BEC孤子從初始位置的穩(wěn)定晶格勢槽中的x1=-6．82處操控到目標位置x2=25．00時，其對應的復合勢演化如圖3(a)所示．而從圖3(b)中可明顯看出，從初始位置到目標位置整個操控過程中復合勢的強度保持不變，只是BEC孤子從初始放置的穩(wěn)定晶格勢槽中的x1=-26．82的A點經過平移拖曳到目標位置x2=25．00的B點，2條復合勢曲線平移了一段距離而已．

圖3 第1種方式操控下復合勢的演化圖

BEC孤子的操控動力學演化如圖4所示．BEC孤子從穩(wěn)定晶格勢槽中的x1=-26．82處向坐標原點左邊平移拖曳操控，目標位置是 x2=25．00．圖 4 中的參數為 A=1．0，V0=-50，V1=0．025，k=0．1，t0=50．0，τ=10．結果表明，通過調制光晶格勢中的操控函數x，實現了BEC孤子穩(wěn)定平移拖曳的動力學操控．需要進一步指出的是，該操控移動過程中的變分動力學系統(tǒng)式(5)～式(8)的數值解與BEC控制方程(1)的直接數值模擬仿真結果非常吻合．

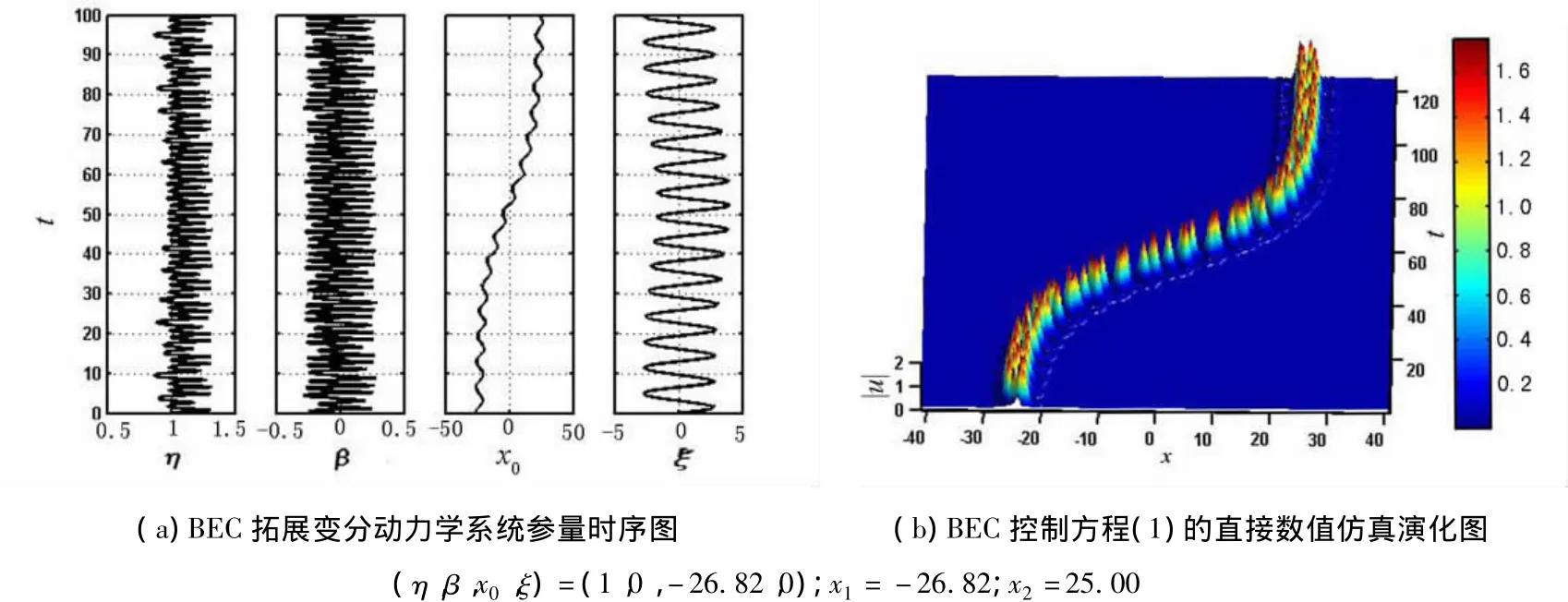
圖4 第1種方式的BEC孤子的操控動力學演化圖

第2種方式是通過復合勢的“周期性振動操控”，操控函數為

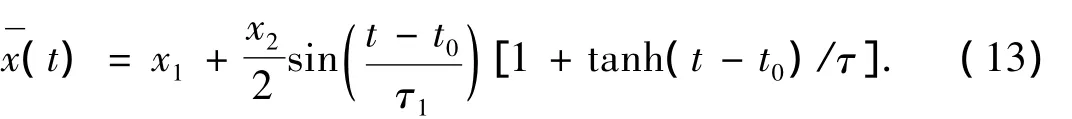
式(13)中:x1，x2，t0和τ的物理意義與第1種方式相同;τ1表示移到目標位置的操控時間．其復合勢與位置和時間之間的演化如圖5所示．圖5中的參數為t0=15．0，τ=0．5，τ1=5．0，k=0．1，A=1．5，V0=-50，V1=0．025，x1=3．74，x2=25．00．先將 BEC孤子放置在穩(wěn)定晶格勢槽中x1=3．74的位置，BEC孤子被穩(wěn)定地囚禁在勢槽中，然后到演化時間t0=15．0時，復合勢中的BEC孤子按正弦曲線軌跡開始移動，再經過5個單位時間拖曳到目標位置;隨著時間的演化，BEC孤子將圍繞初始位置作周期性移動，可以按需要穩(wěn)定移動到周期性移動范圍內的任意位置，BEC孤子的穩(wěn)定操控動力學演化如圖6所示．值得強調的是，該操控移動過程中的變分動力學系統(tǒng)式(5)～式(8)的數值解與BEC控制方程(1)的直接數值模擬仿真結果也照樣非常吻合．

圖5 第2種方式操控復合勢V(x，t)與位置x和時間t之間的演化圖

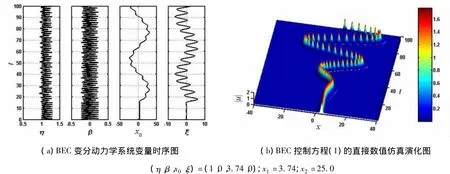
圖6 第2種方式的BEC孤子的操控動力學演化圖

4 結論

如何在BECs的各種外勢場中管理和操控BEC孤子的問題備受研究者的關注．筆者提出了一種拓展變分法，將BEC系統(tǒng)經拓展變分法降階為4個耦合非線性微分方程．該方法引入了啁啾項，使得我們能捕捉到驅使孤子的振幅-寬度波動的二次相位變化的信息，因此，它能更清晰地揭示出在光晶格勢與拋物勢作用下BEC孤子的動力學行為和特征．由它不僅得到了產生精確多穩(wěn)定晶格勢槽數目和外勢場參數決定的臨界比值，而且還得到了2種操控BEC孤子的基本方法．特別需要指出的是，通過調制光晶格勢，成功地實現了BEC孤子從某一穩(wěn)定晶格勢槽為初始位置到任意目標位置的平移拖曳操控和周期性移動操控．這將為與BEC孤子操控相關的宏觀量子現象的實驗和應用提供了良好的理論依據．研究還表明，拓展變分法對BEC孤子系統(tǒng)的描述與數值仿真的結果完全符合．基于拓展變分法對于在光晶格勢與拋物勢作用下BEC孤子的囚禁操控動力學特性描述的有效性，可將該方法拓展到高維BEC孤子的穩(wěn)定性分析和操控問題，具體工作正在進行中．

［1］Anderson M H，Matthews J R，Wieman C E．Observation of Bose-Einstein condensation in dilute atomic vapor［J］．Science，1995，269:198-201．

［2］Anderson B P，Kasevich M A．Tunnel arrays macroscopic quantum interference from atomic［J］．Science，1998，282:1686-1689．

［3］Ovchinnikov Y B，Müller J H，Doery M R，et al．Diffraction of a released Bose-Einstein condensate by a pulsed standing light wave［J］．Phys Rev Lett，1999，83:284-287．

［4］Choi D I，Niu Q．Bose-Einstein condensates in an optical lattice［J］．Phys Rev Lett，1999，82:2022-2025．

［5］Carr L D，Brand J．Pulsed atomic soliton laser［J］．Phys Rev A，2004，70:033607．

［6］Jaksch D，Bruder C，Cirac J I，et al．Cold bosonic atoms in optical lattices［J］．Phys Rev Lett，1998，81:3108-3111．

［7］Parker N G，Proukakis N P，Adams C S．Dark soliton decay due to trap anharmonicity in atomic Bose-Einstein condensates［J］．Phys Rev A，2010，81:033606．

［8］Lasinio M J，Morsch O，Cristiani M，et al．Dark soliton decay due to trap anharmonicity in atomic Bose-Einstein condensates［J］．Phys Rev Lett，2003，91:230406．

［9］Carretero-González R，Promislow K．Localized breathing oscillations of Bose-Einstein condensates in periodic traps［J］．Phys Rev A，2002，66:033610．

［10］Cataliotti F S，Burger S，Fort C，et al．Josephson junction arrays with Bose-Einstein condensates［J］．Science，2001，293:843-846．

［11］Lieb E H，Seiringer R．Proof of Bose-Einstein condensation for dilute trapped gases［J］．Phys Rev Lett，2002，88:170409．

［12］Burlak G，Malomed B A．Dynamics of matter-wave solitons in a time-modulated two-dimensional optical lattice［J］．Phys Rev A，2008，77:053606．

［13］Kutz J N，Holmes P，Evangelides S G，et al．Hamiltonian dynamics of dispersion-managed breathers［J］．J Opt Soc Am B，1998，15:87-96．

［14］Trombettoni A，Smerzi A．Discrete solitons and breathers with dilute Bose-Einstein condensates［J］．Phys Rev Lett，2001，86:2353-2356．

［15］Drazin P G．Nonlinear systems［M］．Cambridge:Cambridge University Press，1992．

［16］Mihalache D，Mazilu D，Lederer F，et al．Stable three-dimensional solitons in attractive Bose-Einstein condensates loaded in an optical lattice［J］．Phys Rev A，2005，72:021601．

［17］楊陽，宗豐德．單泡空化振動系統(tǒng)的動力學數值模擬［J］．浙江師范大學學報:自然科學版，2008，31(3):295-299．