車載炮射擊密集度逐步回歸分析

曹 寧，王曉鋒，徐亞棟，尹 強

（南京理工大學 機械工程學院，南京210094）

車載炮戰略和戰術機動性強，具有快速反應能力、精確打擊能力和自主作戰能力，能滿足現代高科技局部戰爭對火炮戰略機動性及戰術機動性的要求，對車載炮武器系統進行射擊精度分析，尋找影響射擊精度的主要因素，能為新型車載炮總體方案論證、總體設計，射擊法則的制定以及有效地發揮車載炮射擊效率提供合理的依據.射擊精度包括射擊準確度和射擊密集度，前者描述了落點平均位置對瞄準點的系統性偏差，后者描述了落點的隨機散布特性.

車載壓制火炮射擊密集度的確定方法隨著理論和技術水平的發展得到了進一步的完善.如，潘玉田等[1]推導出了有脫靶彈的立靶密集度估計公式；王兆勝等[2]討論了諸元精度、射程、密集度對彈丸首發命中概率的影響；閆雪梅等[3]建立了計算射程及密集度分組試驗的Bayes估計方法；文獻[4]分析了地面密集度隨射角和初速的變化規律；馬春茂等[5]研制了某自行高炮車炮系統的射擊密集度預測軟件.

本文采用回歸分析法研究隨機因素對車載炮射擊密集度的影響，通過對射程和各因素進行標準化，使各種因素量綱得到一致，從而可通過比較回歸系數大小來反映與該系數對應因素的重要性.建立了隨機因素影響程度逐步回歸分析算法，以某車載炮的密集度性能實彈射擊試驗數據為基礎，建立了落點數據的相關系數與射擊密集度之間的統計關系，并分析了各因素對該車載炮射擊密集度的影響.

1 逐步回歸分析算法

假定車載炮發射一組n發彈丸，共有l種因素xj（j＝1，2，…，l）影響其落點坐標，現已獲得各射彈的落點坐標（Xi，Zi），i＝1，2，…，n.如何分析這些因素對車載炮射擊精度的影響及其影響程度，這就必須對所獲得的數據進行統計分析，本文采用逐步回歸分析法對此進行分析.由于對X和Z所采用的回歸原理相同，以X為例進行說明.為使各種因素量綱得到一致，對射程X和因素xj進行標準化處理.

將得到的數據（xi1，xi2，…，xil，Xi）進行標準化：

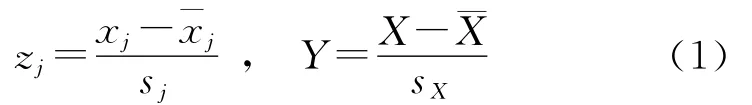
經標準化變換后，zj和Y的幾何平均值為0，標準離差為1，則標準化后的多元回歸方程可表示為

式中，β0為常數項，βj為Y對因素zj的回歸系數，εY為隨機誤差.

將得到的數據經式（1）變換后，代入式（2）得：

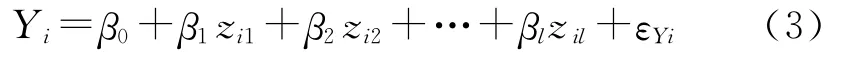
這里假定εYi為獨立同分布，其均值為0，其方差σ2未知，但0＜σ2＜∞.對式（3）進行最小二乘估計，可得βj的估算值j：式中，j（j＝1，2，…，l）為標準化回歸系數，）稱為相關系數矩陣，D＝（dj）為右端列陣）為標準化回歸系數列陣.

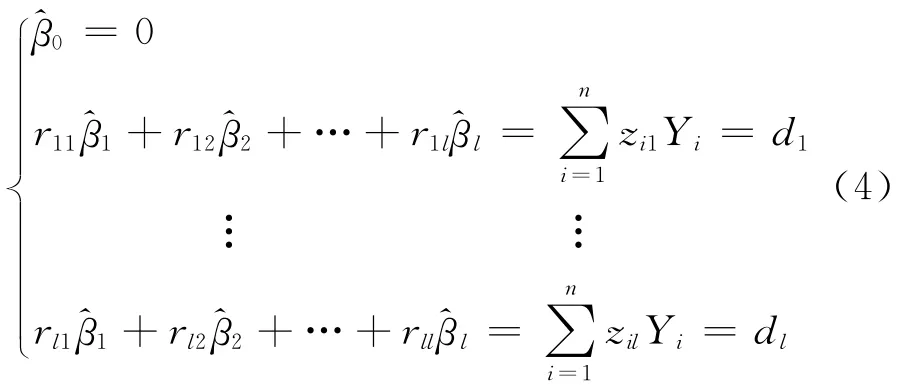
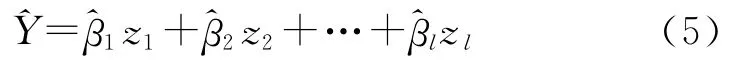
以上給出了多元線性回歸分析的一般形式，本文將給出逐步回歸分析的基本算法流程.令：

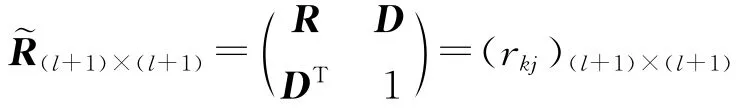
記開始時，對總因素數重新賦值ml＝l，令迭代步數p＝1，回歸方程中的因素數U＝0.

逐步回歸分析法的基本原理：在考慮的全部因素中按其對X的作用大小、顯著程度大小或者貢獻大小，由大到小地逐個引入回歸方程，而對X作用不顯著的因素始終不被引入回歸方程.另外，己被引入回歸方程的因素在引入新因素后也可能失去重要性，而需要從回歸方程中剔除出去.引入一個因素或者從回歸方程中剔除一個因素都稱為逐步回歸的一步，每一步都要進行F分布的檢驗，以保證在引入新因素前回歸方程中只含有對X影響顯著的因素，而不顯著的因素已被剔除.

步驟1 對不包含在回歸方程中的ml個因素，計算偏回歸平方和

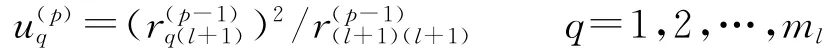
假定第m個因素的偏回歸平方和值最大，即），該因素zm對的回歸貢獻最大，于是優先考慮選入zm.

步驟2 對引入因素zm進行顯著性檢驗.令U＝U＋1，計算統計量：

給定顯著水平α、自由度1和n－U－1，得F1，n－U－1（α），若＜F1，n－U－1（α），則不引進，此時由于貢獻度最大的因素zm都不能引進，其它因素也就不能引進，計算結束.若＞F1，n－U－1（α），表明引入的因素zm對回歸方程的貢獻是顯著的，應引進.并對引進因素zm對應中的主元m進行如下變換，得到變換后的

求解式（6）時一定要遵循以下次序：①非主元m所在行、列，即k≠m、j≠m；②主元m所在行（除主元外），即k＝m，j≠m；③主元m所在列（除主元外），即k≠m，j＝m；④主元m，即k＝m，j＝m.

一旦確定zm要引進回歸方程，必須利用引進zm后已經變換的，按前面相同的方法對回歸方程中已存在的其它因素逐一進行顯著性檢驗，以確定由于因素zm的引進是否需要將其它因素從回歸方程中保留或剔除.

步驟3 因素zm（z（U）＝zm）引入后的回歸方程.標 準 回 歸 系 數 為

標準回歸方程為

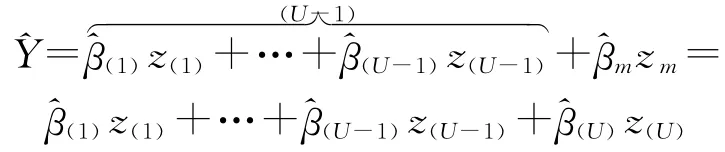
一般回歸方程為

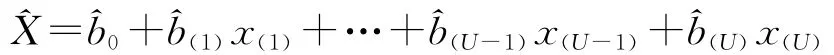
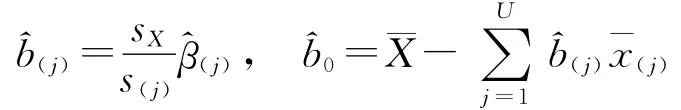
2 靶場試驗數據的相關性分析

為了考察某車載炮的密集度性能，對其進行了實彈射擊試驗.表1給出了5組、每組7發射彈落點坐標（Xc，Zc）的數據和對應的密集度估計值.由表可見，前3組射擊密集度非常差，后2組密集度較好.為此對這5組數據中的落點坐標（X，Z）進行了相關性分析，其相關系數值也在表中給出.對有限射彈的數量，若相關系數｜rXZ｜≥0.8，則認為X和Z有強的相關性；若0.3≤｜rXZ｜＜0.8，則認為有弱的相關性；若｜rXZ｜＜0.3，則認為沒有相關性.前2組的相關性強，密集度很差；后2組相關性弱，密集度很高.為此，圖1給出了該車載炮射擊試驗落點數據的相關系數｜rXZ｜與射擊密集度之間的統計關系圖.圖中，MX為縱向密集度，MZ為橫向密集度.

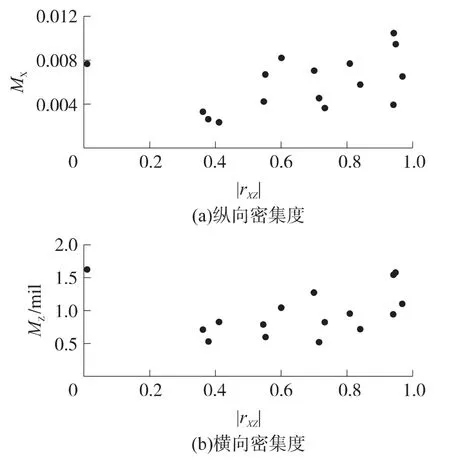
圖1 相關系數與密集度的統計關系

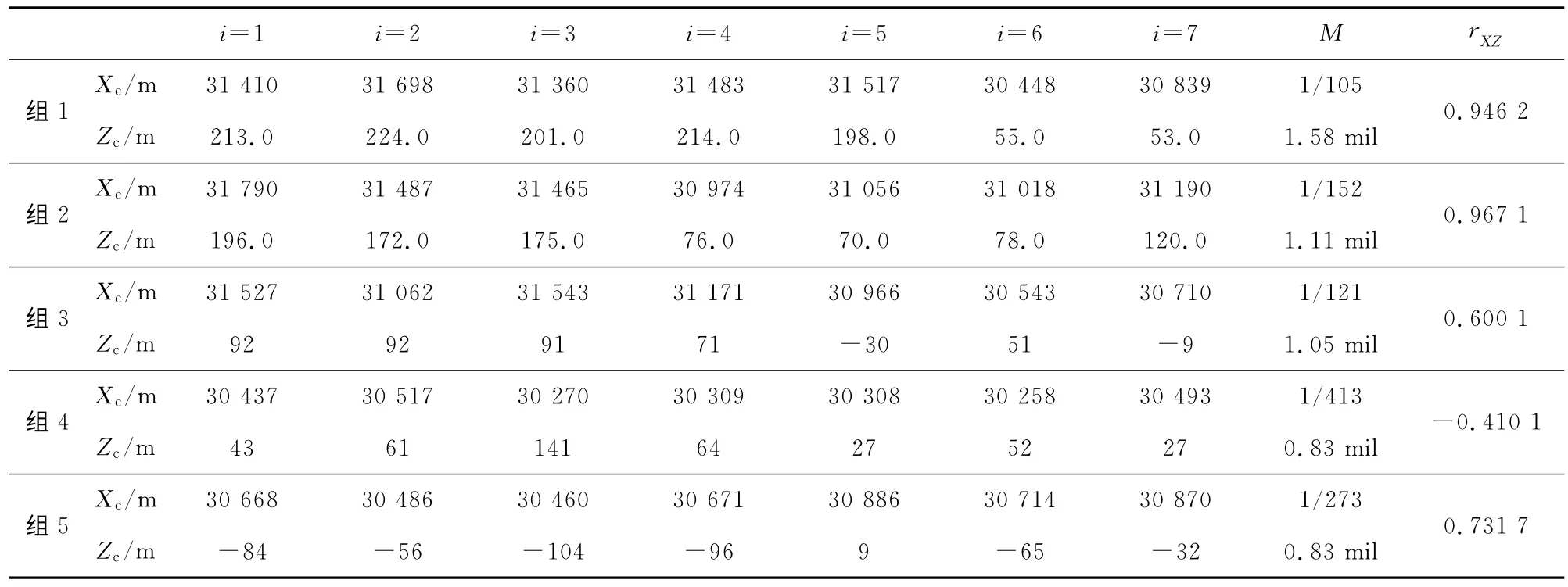
表1 彈落點坐標數據和密集度估計值

從統計結果可以看出，密集度越高，相關系數｜rXZ｜越小；反之，密集度就越低，｜rXZ｜就越大.同時還可以看出，較小的相關系數，不能保證有較高的射擊密集度.對其它射擊試驗的結果進行分析，也得出同樣的結論，如表2所示.若一組彈丸的落點坐標（Xc，Zc）存在較強的相關性，即｜rXZ｜≥0.8，表明車載炮武器系統存在嚴重的系統干擾，應加以認真檢查.

表2 密集度與相關系數的關系

3 射擊密集度影響因素逐步回歸分析

前文對某車載炮密集度實彈射擊試驗數據進行了相關性分析，下面以第一組的數據為例進行密集度影響因素的回歸分析.回歸方程包含的因素越多，回歸平方和越大，剩余的平方和越小，剩余均方也隨之愈小，預測值的誤差也愈小，模擬的效果愈好.但是方程中的因素過多，預報工作量就會越大，其中有些相關性不顯著的預報因子會影響預測的效果.因此，在多元回歸模型中，選擇適宜的因素數目尤為重要.本例中，由于測試條件的局限性選擇因素數目為6.第一組的試驗測試結果見表3.表中，v0為彈丸初速，mq為彈丸質量（kg），Iq為轉動慣量比，εe為彈丸偏心距（mm），p31為駐退機腔3和腔1室的壓力之差（MPa），σh1為高低機齒弧與齒輪相接觸處齒弧側面法向應力（MPa）.因而，一般回歸方程的形式為

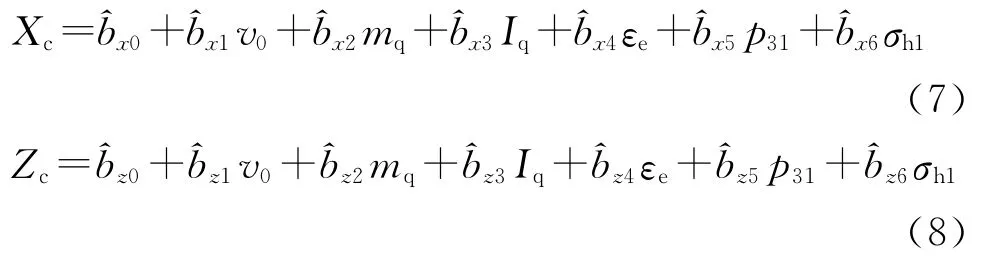
選擇v0、mq、εe作為考察因素的理由是很顯然的，而選擇p31的原因是試圖通過該因素的變化來研究后坐阻力對射擊密集度的影響，選擇σh1的原因是試圖通過該因素來反映身管高低指向的變化規律對密集度的影響.

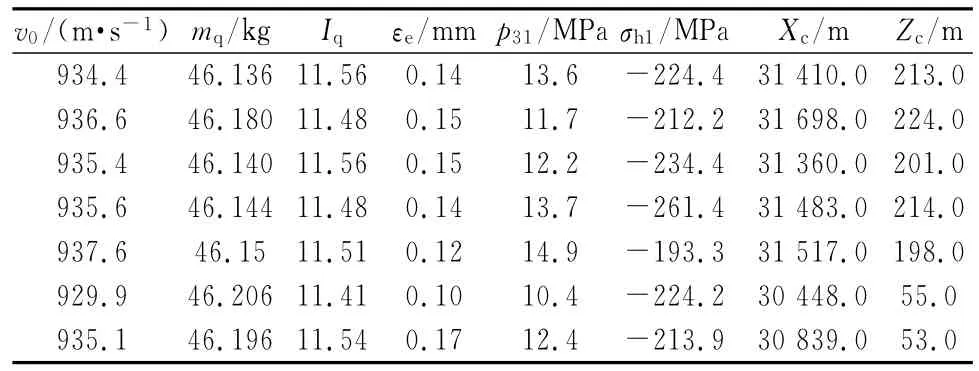
表3 彈丸落點實彈數據表

下面對試驗數據進行逐步回歸分析，將數據分別代入變換式（1），這樣式（7）和式（8）轉換成標準的回歸方程.經最小二乘法運算，其相關系數矩陣為

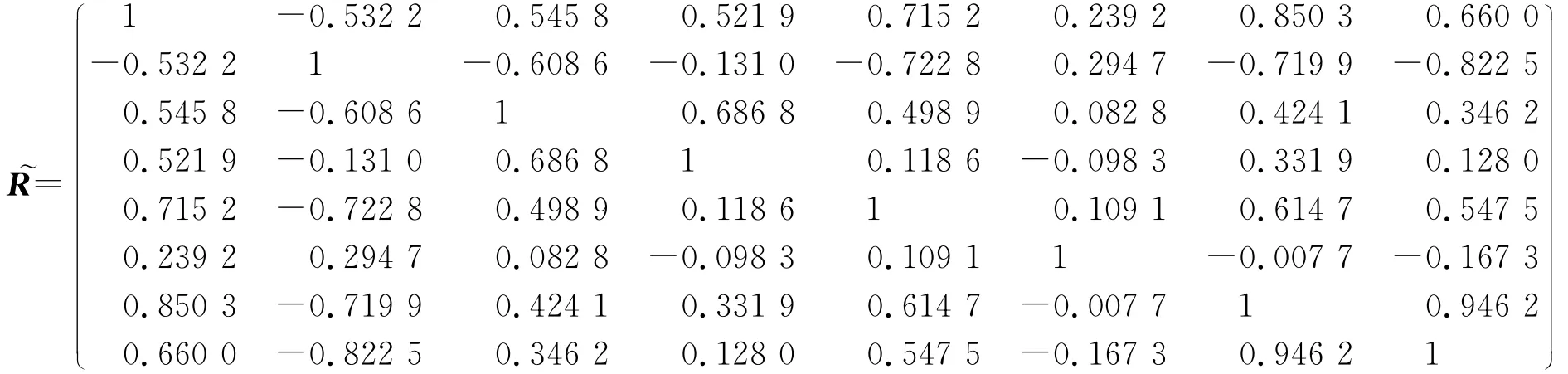
從中可以看出：

①Xc與Zc的相關系數rXZ＝0.946 2，根據相關性檢驗，可知Xc與Zc相關.

②初速v0和彈質量mq均分別與駐退機腔室壓力p31、射程Xc與Zc相關，這符合實際情況.

③轉動慣量比Iq與彈丸偏心距εe相關，這符合實際情況.

④Iq、εe與射程關系不密切，p31與射程有一定的相關性，σh1與射程無相關性.

分別對Xc和Zc進行逐步回歸分析，得到Xc與Zc的回歸方程分別為

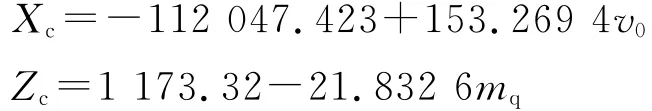
由逐步回歸分析結果可以看出，考慮v0、mq、Iq、εe、p31和σh1等因素時，影響彈丸縱向射程的主要因素是初速，影響橫向側偏的主要因素是彈質量.對其它組數據分析亦有類似結果.

4 結束語

本文以某車載炮的密集度性能實彈射擊試驗數據為基礎，采用逐步回歸分析法對車載炮射擊密集度的影響因素進行分析，給出了該車載炮射擊試驗落點數據的相關系數與射擊密集度之間的統計關系.研究了彈丸初速、彈質量和彈丸偏心距等因素對車載炮射擊密集度的影響.回歸分析結果表明，影響彈丸縱向射程的主要因素是初速，影響橫向側偏的主要因素是彈質量，與實彈射擊結果相吻合，驗證了本文所提逐步回歸分析法用于車載炮射擊精度影響因素分析的可行性和有效性.

[1]潘玉田，馬新謀.自動火炮射彈密集度估計[J].火炮發射與控制學報，2006，（2）：38－42.PAN Yu－tian，MA Xin－mou.Shot density estimation of automatic gun[J].Journal of Gun Launch ＆ Control，2006，（2）：38－42.（in Chinese）

[2]王兆勝，郭錫福.諸元精度與密集度對命中概率的影響[J].彈道學報，2003，15（1）：64－68.WANG Zhao－sheng，GUO Xi－fu.Influence on hitting probability by accuracy of firing data and dispersion[J].Journal of Ballistics，2003，15（1）：64－68.（in Chinese）

[3]閆雪梅，文艷，邱叢禮.射程與密集度分組試驗的Bayes估計[J].彈道學報，2006，18（2）：80－83.YAN Xue－mei，WEN Yan，QIU Cong－li.Bayesian estimation of range and dispersion of grouping trial[J].Journal of Ballistics，2006，18（2）：80－83.（in Chinese）

[4]王兆勝.射角和初速對地面密集度的影響[J].火炮發射與控制學報，2008，（4）：1－4.WANG Zhao－sheng.Influence of departure angle ＆ muzzle－velocity on ground density[J].Journal of Gun Launch ＆ Control，2008，（4）：1－4.（in Chinese）

[5]馬春茂，孫逢春，李魁武，等.自行高炮車炮系統射擊密集度預測研究[J].兵工學報，2002，23（2）：251－254.MA Chun－mao，SUN Feng－chun，LI Kui－wu，et al.A prediction on the dispersion accuracy of the gun－vehicle system in self－propelled[J].Acta Armamentarii，2002，23（2）：251－254.（in Chinese）

[6]邱瑾，牟少鋒，楊軍.自行火炮自動瞄準精度數據分析[J].火力與指揮控制，2007，32（1）：105－107.QIU Jin，MOU Shao－feng，YANG Jun.Data analysis for aiming accuracy of self－propelled gun[J].Fire Control and Command Control，2007，32（1）：105－107.（in Chinese）