考慮動態(tài)接觸參數(shù)的某型導(dǎo)彈發(fā)射動力學(xué)分析

劉馨心，徐宏斌，張亮亮，褚福磊

（1.清華大學(xué) 精密儀器與機械學(xué)系，北京100084；2.西安現(xiàn)代控制技術(shù)研究所，西安710065）

初始擾動是各類武器研制需要解決的一個重要問題.對導(dǎo)彈系統(tǒng)來說，過大的初始擾動會加重制導(dǎo)系統(tǒng)負擔(dān)，甚至造成導(dǎo)彈失控.目前對初始擾動的研究主要考慮了推力偏心、質(zhì)量偏心、動不平衡[1]等因素，而考慮結(jié)構(gòu)間隙帶來的系統(tǒng)動特性影響的分析不多見.

由于設(shè)計需要或加工誤差等原因，導(dǎo)彈發(fā)射系統(tǒng)不可避免地存在運動副間隙，導(dǎo)彈在發(fā)射出筒過程中的動力學(xué)特性會受到間隙的影響，從而影響導(dǎo)彈的初始擾動.因此，在導(dǎo)彈發(fā)射系統(tǒng)建模過程中考慮運動副間隙影響，引入接觸碰撞模型，將有助于更加真實、準(zhǔn)確地研究系統(tǒng)參數(shù)對導(dǎo)彈初始擾動的影響，為導(dǎo)彈發(fā)射系統(tǒng)的設(shè)計以及提高發(fā)射精度提供參考.

研究系統(tǒng)間隙碰撞問題的關(guān)鍵是要解決接觸碰撞階段的動力學(xué)模型，而模型的難點在于接觸參數(shù)的確定[2～5].本文以某單位研制的反坦克導(dǎo)彈武器系統(tǒng)為研究對象，基于接觸變形碰撞模型，考慮接觸剛度、阻尼系數(shù)和穿透量的動態(tài)變化，利用動力學(xué)軟件建立了研究對象的動力學(xué)模型，通過數(shù)值仿真計算得到了系統(tǒng)的動力學(xué)響應(yīng).

1 接觸碰撞模型的建立

1.1 碰撞接觸力模型

經(jīng)典碰撞模型認為碰撞在瞬間完成，忽略了接觸過程，因此無法給出碰撞發(fā)生時的接觸力變化和碰撞時間等信息，但是系統(tǒng)的運動參數(shù)動態(tài)響應(yīng)是需要關(guān)注的重要特性，因此，采用等效的接觸變形碰撞模型來描述系統(tǒng)各部件之間的接觸較為合適.

DUBOWSKY[2]提出即使在較小的碰撞速度下，碰撞點鄰域內(nèi)仍會存在微小變形，并由彈簧阻尼系統(tǒng)來等效碰撞力的大小，其廣義形式可表示為

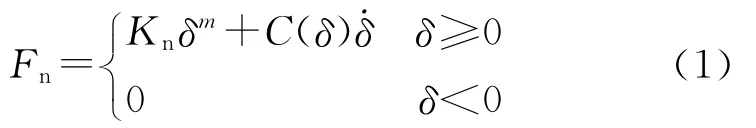
式中，F(xiàn)n為接觸點處法向接觸力，Kn為等效接觸剛度，C（δ）是與δ有關(guān)的阻尼因子，δ和為接觸點法向穿透深度及法向相對速度，非線性指數(shù)因子m≥1.不同的m、Kn和C（δ）代表不同的模型，常見的有基于Herts理論的接觸模型、基于DUBOWSKY線性化處理的碰撞模型以及非線性等效彈簧阻尼模型等，但這幾種模型里的接觸參數(shù)均是與系統(tǒng)運動特性無關(guān)的量.

HUNTER[3]分析了2個彈性球的碰撞運動過程，如圖1所示，質(zhì)量m2的小球以速度v0撞向質(zhì)量m1的小球，推導(dǎo)得撞擊過程中的最大撞擊力為

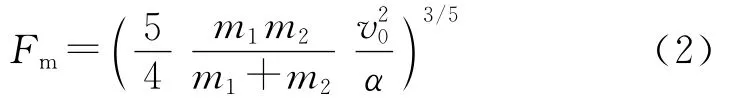
最大擠壓量為

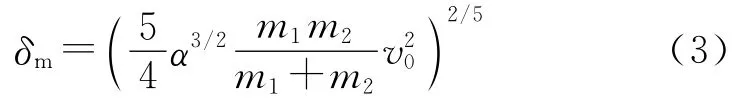
式中，

式中，E、ν、R分別為小球的楊氏模量、泊松比和曲率半徑.

對于圓柱與圓筒碰撞，此時的α為

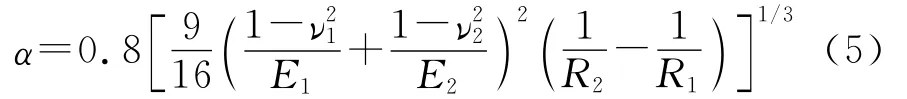
由式（2）、式（3）可看出，F(xiàn)m和δm均是與物體相對碰撞速度有關(guān)的量.文獻[4]通過對轉(zhuǎn)子和定子碰撞過程的線性化處理，并對比文獻[3]的計算結(jié)果，得到了兩剛體碰撞的線性當(dāng)量化接觸剛度計算公式.徐振欽等人[5]將這種碰撞模型引入到火箭武器發(fā)射過程中的彈管接觸碰撞多體系統(tǒng)動力學(xué)模型中，得到了較好的計算結(jié)果.

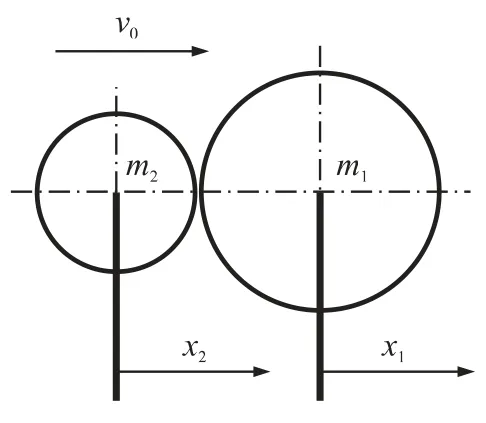
圖1 兩彈性球相撞

本文采用線性當(dāng)量化的方法，用等效彈簧－阻尼模型來模擬局部撞擊處的彈性擠壓這一非線性過程，其中彈簧剛度為K，阻尼系數(shù)為c，線性當(dāng)量化的彈簧－阻尼模型如圖2所示.

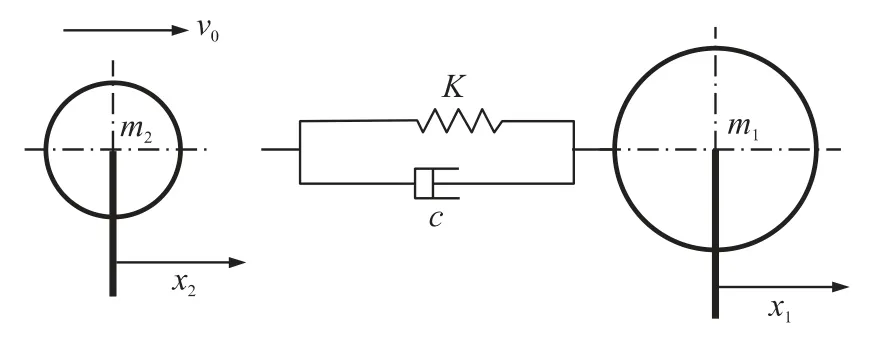
圖2 線性當(dāng)量化的彈簧－阻尼模型

當(dāng)彈簧－阻尼系統(tǒng)處于接觸狀態(tài)時，系統(tǒng)的運動微分方程為

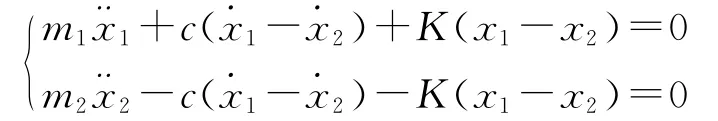
初始條件x1（0）＝0，x2（0）＝0，1（0）＝0，2（0）＝v0，通過正則化方法計算得到2個小球的位移響應(yīng)為

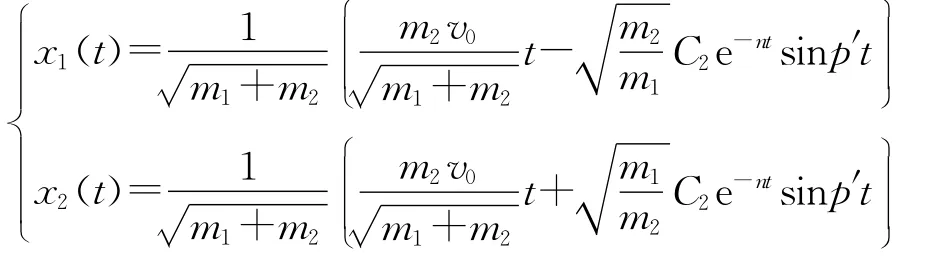
速度響應(yīng)為

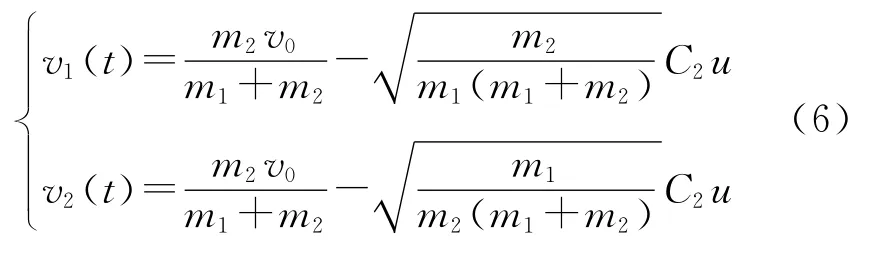
式中，

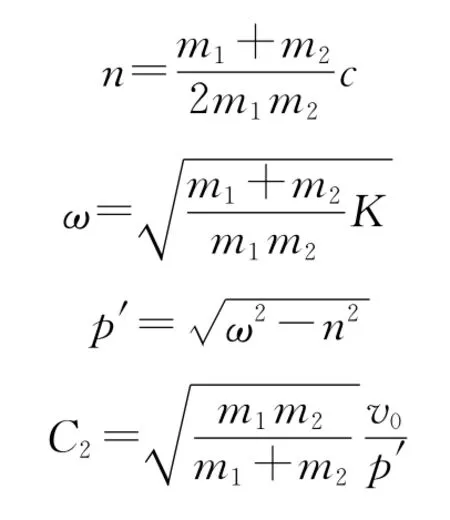
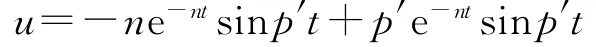
則兩小球在相撞過程中的相對距離為

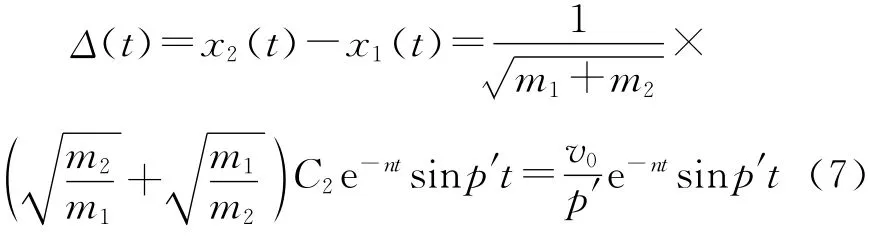
設(shè)tm為碰撞過程達到最大擠壓量的時刻，此時（tm）＝0，彈簧阻尼系統(tǒng)產(chǎn)生的作用力由彈簧提供，則：

將式（2）和式（3）代入式（8），得線性當(dāng)量化的剛度系數(shù)K為

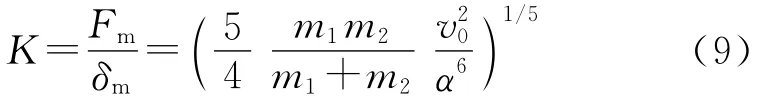
阻尼系數(shù)的存在導(dǎo)致碰撞前后的能量損失.設(shè)時刻ts為兩小球碰撞結(jié)束時刻，則有：

取該分析模型具有物理意義的時刻，得到：

將式（11）代入式（6），得到兩小球碰撞結(jié)束時的能量為

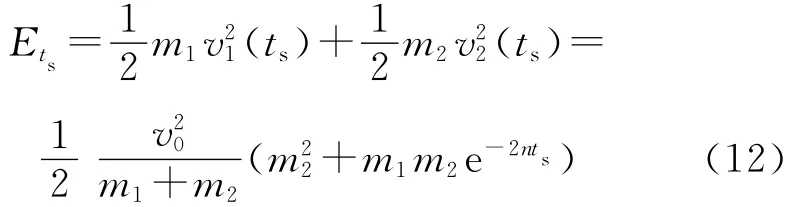
用恢復(fù)系數(shù)法求得兩小球碰撞結(jié)束時的能量為

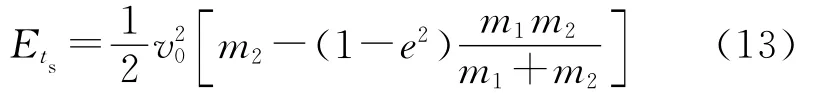
式中，e為恢復(fù)系數(shù).

2種計算方法求得的能量值相等，將式（12）和式（13）對比化解即可得到線性當(dāng)量化后的阻尼系數(shù)為

這與文獻[6]得到的結(jié)果一致.

將式（9）和式（14）代入式（1），取m＝1便可得到用等效線性當(dāng)量化的彈簧－阻尼模型處理的接觸點處的法向接觸力.

從式（3）、式（9）和式（14）可以看出，該接觸碰撞模型的等效接觸剛度、阻尼系數(shù)和穿透深度除了與接觸處的材料參數(shù)有關(guān)外，還與相對碰撞速度有關(guān)，它們在運動仿真過程中是變量.

1.2 摩擦力模型

接觸點的切向相對運動分為相對滑移和粘滯2種情況.接觸滑移狀態(tài)時可認為其摩擦力作用符合庫倫摩擦定律，即摩擦力大小與法向接觸力大小成正比，而方向與相對滑移速度方向相反：

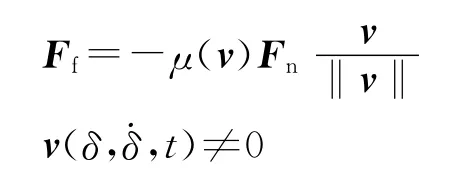
式中，F(xiàn)f為接觸處的滑動摩擦力；μ（v）為摩擦系數(shù)；接觸點的相對滑移速度v（δ，，t）≠0.而粘滯狀態(tài)的切向接觸力與靜摩擦系數(shù)有關(guān).接觸點處的運動量決定這2種狀態(tài)的相互切換.

ADAMS中為了避免數(shù)值計算中速度方向變化時出現(xiàn)摩擦力突變，摩擦系數(shù)μ處理為與相對滑移速度v（δ，t）有關(guān)的變化曲線，其表達式為

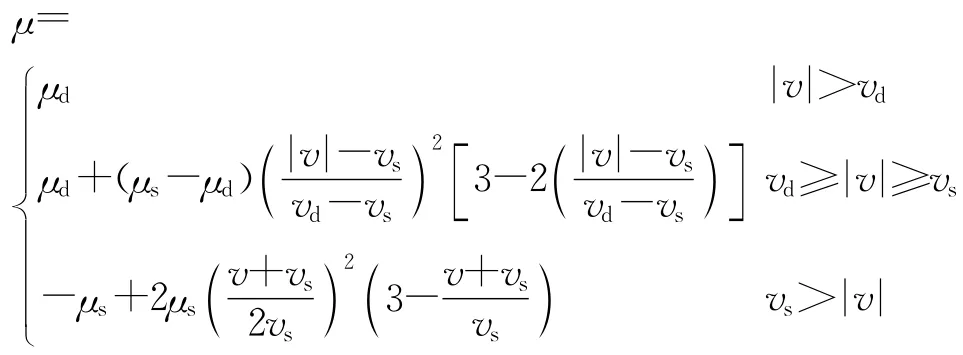
式中，vs和vd分別為粘滯轉(zhuǎn)換速度和動靜摩擦轉(zhuǎn)換速度，μs和μd分別為靜摩擦系數(shù)、動摩擦系數(shù)，它們與兩接觸物體的材料屬性以及表面粗糙度等因素有關(guān).

2 多體系統(tǒng)動力學(xué)模型

2.1 虛擬樣機模型

本文研究的導(dǎo)彈發(fā)射系統(tǒng)是一個復(fù)雜的動力學(xué)系統(tǒng)，為使仿真模型盡量簡化而又真實、合理，將其簡化為由導(dǎo)彈、發(fā)射筒、制導(dǎo)箱、方向機、高低機和發(fā)射基座等主要部分組成的多體系統(tǒng)，各部分之間的拓撲關(guān)系如圖3所示.

圖3 系統(tǒng)構(gòu)件拓撲關(guān)系

利用UG建立系統(tǒng)的三維實體模型，確定構(gòu)件間的初始位置及裝配關(guān)系，并通過其與ADAMS的通用接口導(dǎo)入，建立虛擬樣機模型進行動力學(xué)仿真分析，主要過程如下.

①整個系統(tǒng)包括彈體、發(fā)射筒、制導(dǎo)箱、方向機、高低機、發(fā)射基座等33個主要剛體，包括移動副、旋轉(zhuǎn)副、圓柱副等在內(nèi)的31個運動約束，包括彈與筒，筒與4個滑軌，筒與閉鎖器，基座3個架腿與地面等18個接觸碰撞力；

②發(fā)動機推力和燃氣流后坐力通過實彈射擊測得，形成6個AKISPL樣條函數(shù)；

③方向機阻尼油的作用特性由一個作用力矩等效，力矩大小等于阻尼系數(shù)與相對回轉(zhuǎn)角速度的乘積，力矩方向繞方向機的回轉(zhuǎn)方向且與其運動角速度方向相反；

④1個傳感器監(jiān)測導(dǎo)彈運行過程，當(dāng)導(dǎo)彈出筒時暫停仿真，輸出結(jié)果；

⑤不考慮發(fā)射筒、彈體的不平度，不考慮加工誤差引起間隙分布的隨機性；

⑥不考慮射手在射擊過程的作用力，即仿真過程為無控仿真.

2.2 接觸參數(shù)的確定

該型號導(dǎo)彈系統(tǒng)的彈體與發(fā)射筒質(zhì)量處于同一數(shù)量級.彈體定位塊與發(fā)射筒的接觸碰撞相當(dāng)于圓柱體與圓筒碰撞，設(shè)δ0為彈筒間隙，導(dǎo)彈半徑為r，發(fā)射筒內(nèi)半徑為R，R＝r＋δ0，則有：

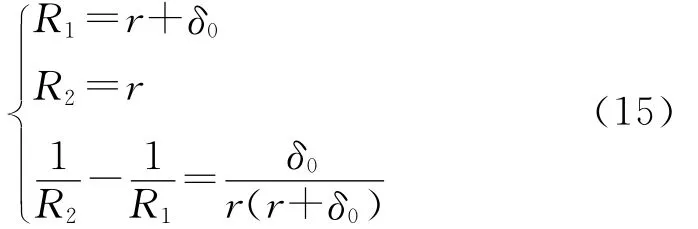
將式（15）分別代入式（3）、式（5）、式（9）和式（14），得導(dǎo)彈與發(fā)射筒接觸碰撞的動態(tài)接觸剛度、阻尼系數(shù)和穿透深度.

試驗射擊時，發(fā)射系統(tǒng)置于水泥地面，基座支架腿與地面的接觸面為弧形.因此將水泥地面看成一個曲率無窮大、質(zhì)量無窮大的鋼球，架腿與地面的接觸碰撞相當(dāng)于球形與球形的碰撞，且有：

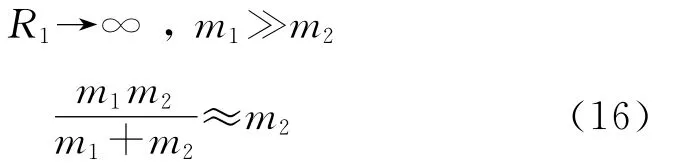
將式（16）分別代入式（3）、式（4）、式（9）和式（14）得架腿與地面的動態(tài)接觸剛度、阻尼系數(shù)和穿透深度.

類似地，計算其它接觸碰撞力.在Adams中，碰撞力的類型選用“Solid to Solid”，利用Adams強大的幾何搜索引擎判斷幾何體間的相對位置關(guān)系，接觸發(fā)生后調(diào)用接觸參數(shù)的計算程序，計算法向接觸力和切向摩擦力.

3 動力學(xué)仿真分析

影響導(dǎo)彈初始擾動的因素很多，如導(dǎo)彈安裝誤差、發(fā)動機推力偏差、導(dǎo)彈的動不平衡、初始瞄準(zhǔn)角、回轉(zhuǎn)器阻尼特性等，且許多干擾量都具有隨機性.為重點研究線性當(dāng)量化的接觸碰撞模型是否能較好地模擬系統(tǒng)的間隙接觸問題，這里將各干擾量考慮成固定值，通過多次實驗測量得到干擾量，并將其代入仿真模型進行模型驗證.

3.1 仿真模型驗證

以0°方向機初始方位瞄準(zhǔn)角和2.5°高低機初始高低瞄準(zhǔn)角的常溫、室內(nèi)、無控發(fā)射作為基本初始條件，彈筒間隙、導(dǎo)彈質(zhì)心偏移、發(fā)動機推力及燃氣流沖擊力的軸向分力和徑向偏差采用實驗測量均值，將前面所述接觸參數(shù)確定的方法代入該導(dǎo)彈發(fā)射系統(tǒng)的動力學(xué)模型中，仿真得到各構(gòu)件的動力學(xué)響應(yīng)曲線.將部分仿真結(jié)果與實驗數(shù)據(jù)進行對比，列于表1中.表中，vr為導(dǎo)彈出筒速度，t為出筒時間，ωrx、ωry和ωrz分別為導(dǎo)彈的傾斜角速度、偏航角速度和俯仰角速度，αr、βr和γr分別為導(dǎo)彈的傾斜角、偏航角和俯仰角.表1中，實驗值是多次室內(nèi)常溫?zé)o控發(fā)射實驗所測得的導(dǎo)彈姿態(tài)的平均值.導(dǎo)彈出筒時的俯仰角、偏航角為負值，這表明導(dǎo)彈出筒時的姿態(tài)為低頭右偏航，“—”表示無實測值.

表1 仿真結(jié)果與實驗結(jié)果對比

由表1可知，仿真結(jié)果的導(dǎo)彈出筒姿態(tài)與多次實驗的平均值很接近，說明用該模型來分析系統(tǒng)的動特性是可信的.

3.2 溫度對初始擾動的影響

實驗結(jié)果表明，發(fā)射溫度的變化會對導(dǎo)彈的初始擾動產(chǎn)生影響.通過實驗獲取燃料燃燒在常溫、低溫和高溫環(huán)境下對導(dǎo)彈產(chǎn)生的推力，并將實測結(jié)果輸入到系統(tǒng)模型中，其它因素保持不變，計算得到不同溫度下導(dǎo)彈運動姿態(tài)隨時間的變化曲線，如圖4所示.

圖4 3種狀態(tài)下導(dǎo)彈運動姿態(tài)變化曲線

從圖4可以看出，高溫發(fā)射時導(dǎo)彈出筒時間最短，低溫發(fā)射時出筒時間最長.相比常溫和高溫狀態(tài)，低溫發(fā)射的導(dǎo)彈出筒傾斜角速度和俯仰角速度最大，偏航角速度更小.相比傾斜角速度和偏航角速度，由于俯仰角速度會受到導(dǎo)彈重力作用而下落，因此，俯仰角速度是需要重點關(guān)注的指標(biāo).綜合來看，低溫發(fā)射的初始擾動更大.不同溫度造成不同的初始擾動，其本質(zhì)為不同溫度下的發(fā)動機推力及推力偏差不同，這和發(fā)動機推力偏差對導(dǎo)彈出筒擾動影響較大的結(jié)論是吻合的.

3.3 初始方位瞄準(zhǔn)角對初始擾動的影響

導(dǎo)彈運動姿態(tài)隨方向機初始方位瞄準(zhǔn)角β0大小變化的部分仿真結(jié)果如圖5所示.

其中，0°方位表示2條支架腿朝后且一條支架腿朝發(fā)射方向的布置方式，180°方位與其相反.180°布置方式的出筒傾斜角速度和俯仰角速度均大于0°布置方式.因此，選擇3條支架腿布置方式時，2支架腿朝后且一條支架腿朝發(fā)射方向的方式更為合理.

同時，從仿真結(jié)果趨勢來看，初始方位瞄準(zhǔn)角在40°～60°之間，導(dǎo)彈俯仰方向初始擾動最大，但在360°方位射角內(nèi)，導(dǎo)彈的出筒初始擾動幅值沒有超過0.2rad/s，滿足控制系統(tǒng)的穩(wěn)定性要求.

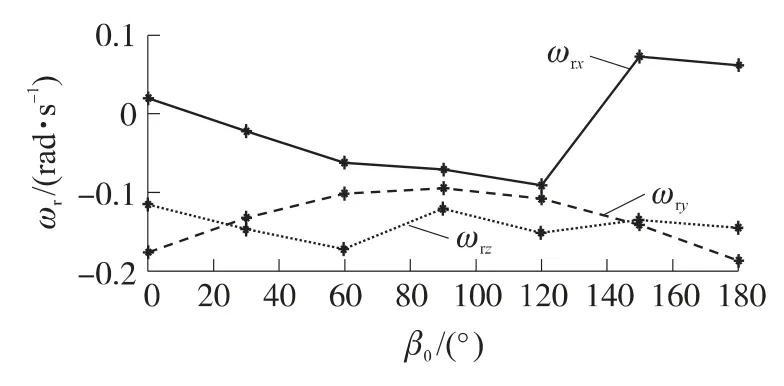
圖5 導(dǎo)彈出筒姿態(tài)隨初始方位瞄準(zhǔn)角的變化曲線

3.4 阻尼器特性對系統(tǒng)動特性的影響

制導(dǎo)箱是整個發(fā)射系統(tǒng)的重要部件，其運動特性將直接影響到導(dǎo)彈控制系統(tǒng)的穩(wěn)定性，而方向機的阻尼器是為保證系統(tǒng)穩(wěn)定性而設(shè)計的.圖6～圖8給出了方向機、制導(dǎo)箱和發(fā)射筒從導(dǎo)彈開始發(fā)射直到運動收斂至穩(wěn)定時，各自的角速度曲線.圖中ωh為方向機的回轉(zhuǎn)角速度，ωf為制導(dǎo)箱的俯仰角速度，ωt為發(fā)射筒的俯仰角速度，ch為阻尼器的阻尼系數(shù).

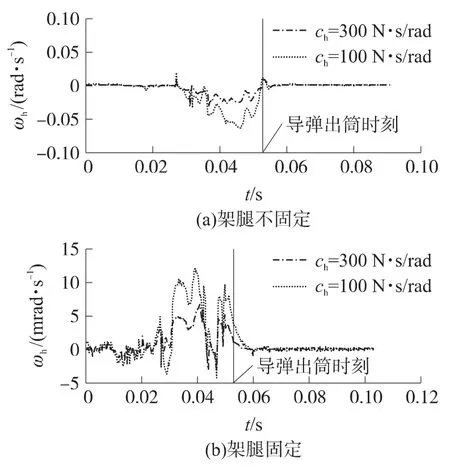
圖6 方向機回轉(zhuǎn)角速度運動曲線

圖6表明，方向機在阻尼器作用下迅速收斂，且改變支架腿與地面的連接方式為固定連接時，方向機的初始擾動量大大減小.

圖7表明，導(dǎo)彈發(fā)射出筒后，制導(dǎo)箱在初始激勵下經(jīng)過了約60ms收斂至0，支架腿與地面的固定連接方式使得制導(dǎo)箱初始擾動迅速減小.

同時，從圖6、圖7的對比曲線可以看出，阻尼器的阻尼系數(shù)對收斂速度影響不大，但對方向機以及與之相關(guān)的制導(dǎo)箱、發(fā)射筒等的回轉(zhuǎn)角速度大小影響很大.從仿真結(jié)果來看，為滿足戰(zhàn)術(shù)指標(biāo)要求，阻尼器阻尼系數(shù)在滿足射手舒適性要求的情況下，應(yīng)盡量大于300N·s/rad.

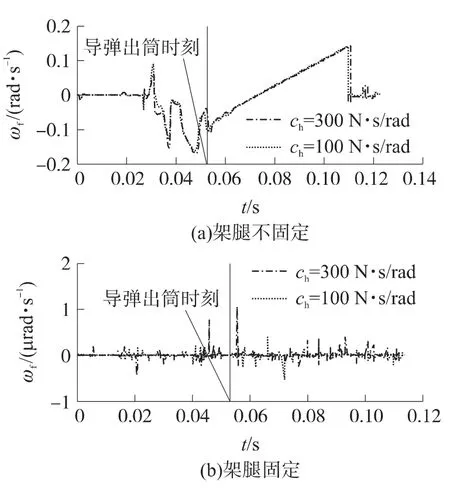
圖7 制導(dǎo)箱俯仰角速度運動曲線

圖8表明，在初始激勵下，發(fā)射筒經(jīng)過了約60ms收斂至0，支架腿與地面的固定連接方式減小了其初始擾動，但因為滑軌間隙的存在，仍然存在一定量的初始擾動，但增大了發(fā)射筒的運動收斂速度，系統(tǒng)穩(wěn)定性更好.

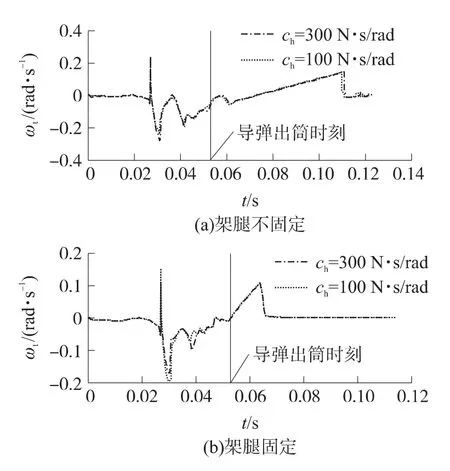
圖8 發(fā)射筒俯仰角速度運動曲線

圖9給出了支架腿不固定和固定2種情況下，導(dǎo)彈發(fā)射出筒過程的運動姿態(tài)曲線.從圖9看到，固定支架腿的連接方式使導(dǎo)彈偏航和俯仰運動幅值更小，運動更平穩(wěn).

綜合分析可知，增大架腿與地面的抓力可以增強系統(tǒng)的穩(wěn)定性.實際戰(zhàn)場運用時，由于有射手作用力的存在，射手利用身體施力于發(fā)射裝置上也會使得系統(tǒng)的運動擾動減小，穩(wěn)定性更好.

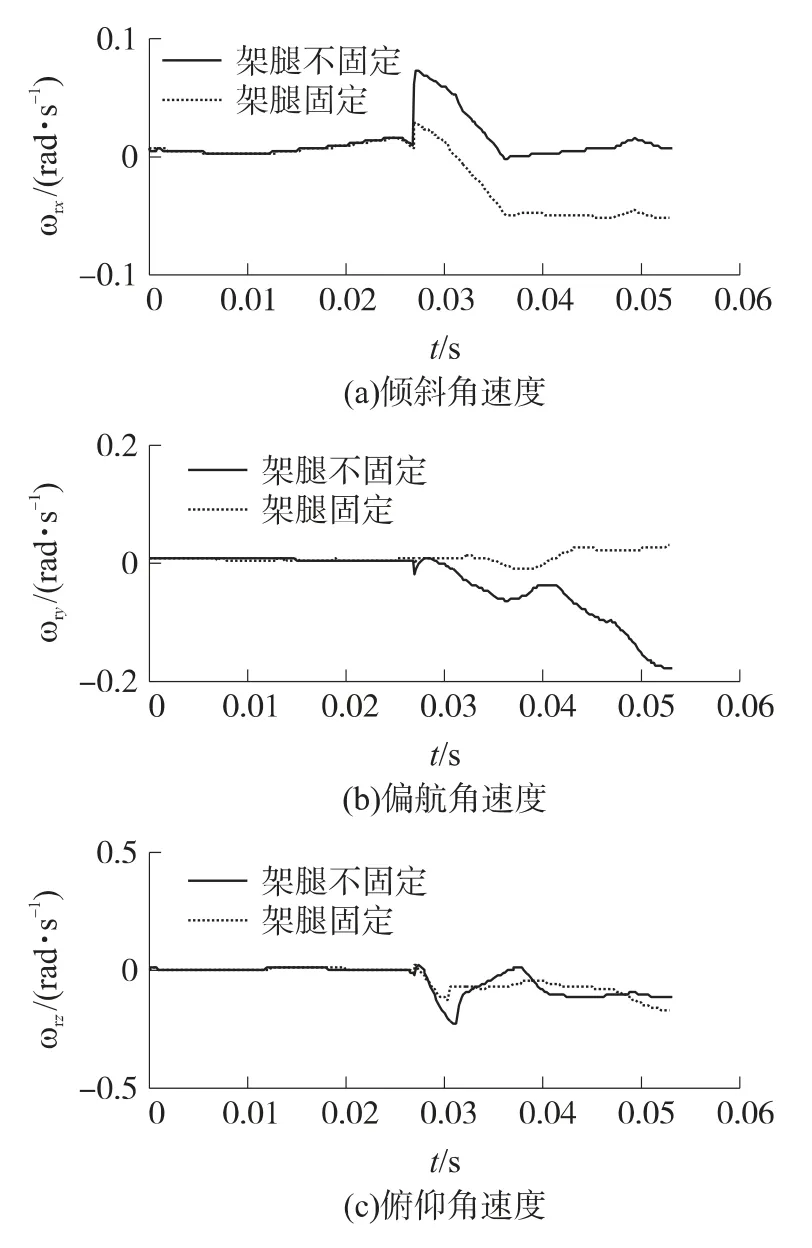
圖9 導(dǎo)彈出筒過程運動姿態(tài)曲線

4 結(jié)束語

基于彈性理論，將考慮動態(tài)接觸剛度、阻尼系數(shù)和穿透量的接觸變形碰撞模型應(yīng)用于某型號反坦克導(dǎo)彈發(fā)射系統(tǒng)的動力學(xué)建模中，借助ADAMS軟件得到了系統(tǒng)的動力學(xué)響應(yīng)結(jié)果.仿真結(jié)果基本符合試驗結(jié)果，證明了該碰撞模型是有效的.

①不同溫度引起不同發(fā)動機推力偏差，導(dǎo)致導(dǎo)彈初始擾動的變化，低溫發(fā)射條件下的初始擾動較大.

②初始方位瞄準(zhǔn)角對導(dǎo)彈初始擾動有影響，但仿真結(jié)果都滿足戰(zhàn)技指標(biāo).兩腿朝后的布置方式優(yōu)于兩腿朝前的布置方式.

③方向機阻尼特性對系統(tǒng)穩(wěn)定性有較大影響，阻尼器阻尼系數(shù)應(yīng)在滿足射手舒適性要求范圍內(nèi)盡可能大于300N·s/rad.

④支架腿與地面的連接方式對導(dǎo)彈系統(tǒng)的動特性有影響，增大支架腿的抓地力能使系統(tǒng)的初始擾動較小，穩(wěn)定性增強.

通過對本文提出的模型進行仿真分析，可以得到發(fā)射系統(tǒng)在不同條件下的作戰(zhàn)特性，這對該型號的武器系統(tǒng)性能分析和設(shè)計改進具有一定的參考價值.

[1]王志軍，趙文宣.火箭彈起始擾動數(shù)值仿真研究[J].彈道學(xué)報，1996，8（3）：69－74.WANG Zhi－jun，ZHAO Wen－xuan.Numerical simulation on the initial disturbance of rockets[J].Journal of Ballistics，1996，8（3）：69－74.（in Chinese）

[2]DUBOWSKEY S，DECK J F.On the limitation of predictions of the dynamic response of machines with clearance connections[J].ASME J of Machine Design，1994，116：883－841.

[3]HUNTER S C.Energy absorbed by elastic waves during impact[J].J Mech Phys Solids，1957，5（1）：162－171.

[4]馬建敏，張文，鄭鐵生.轉(zhuǎn)子系統(tǒng)瞬時撞擊剛度的定量計算方法[J].應(yīng)用力學(xué)學(xué)報，2003，20（2）：68－71.MA Jian－min，ZHANG Wen，ZHENG Tie－sheng.Quantitative calculation method of instantaneous impact stiffness of rotor system[J].Chinese Journal of Applied Mechanics，2003，20（2）：68－71.（in Chinese）

[5]徐振欽，馬大為，樂貴高.基于碰撞接觸的彈管多體動力學(xué)建模與仿真[J].系統(tǒng)仿真學(xué)報，2007，19（5）：965－968.XU Zhen－qin，MA Da－wei，LE Gui－gao.Multibody dynamics modeling and simulation of rocket and launching tube based on contact－impact theory[J].Journal of System Simulation，2007，19（5）：965－968.（in Chinese）

[6]ANAGNOSTOPOULOS S A.Equivalent viscous damping for modeling inelastic impacts in earthquake pounding problems[J].Earthquake Engineering and Structural Dynamics，2004，33（8）：897－902.