改進紙漿漂白溫度控制系統設計

尤 斌 彭 晗 胡慕伊，* 熊智新

(1.南京林業大學江蘇省制漿造紙科學與技術重點實驗室，江蘇南京，210037;2.南京林業大學化學工程學院，江蘇南京，210037)

在紙漿多段連續漂白過程中，為了穩定漂白過程中的工藝條件，使紙漿達到預期的白度，必須對漂白塔中的漿料溫度進行控制。在實際過程中，漂白塔上部溫度采用蒸汽加熱;中部溫度不控制;下部溫度采用加冷卻水的方法控制，經過氯化和堿處理后的漿料通過蒸汽加熱經過雙輥混合器進入漂白塔中［1］。通常采用常規PID控制，也有文獻提出采用單神經元PID［2］控制方案，或者基于遺傳算法 PID［3］控制方案等智能PID控制，歸根結底以上控制方案都是單回路控制，通過調整蒸汽閥門開度來調整漂白塔上部溫度。然而，漂白塔容積比較大，被控對象的干擾因素比較多，如漂白塔上部來自投料方面的干擾:漿料濃度不勻，檢測到的漿料流量、溫度與實際值不一致;來自蒸汽方面的干擾:流量、壓力等波動［4］。

考慮以上問題，對單回路系統進行改進，以漂白塔上部溫度作為主控變量，蒸汽流量作為副控變量，采用最小二乘法辨識過程對象參數。主控制器采用模糊PID控制器在線整定控制參數，副控制器采用純比例控制器，并對主副控制器加入Smith預估器，進一步補償滯后環節。

1 最小二乘辨識漂白過程對象參數

最小二乘法是利用過程的任意輸入輸出的離散數據進行，用計算機巡回檢測，采集數據十分方便，加之計算機能快速精確地運算，解析過程方便，因此，在辨識對象及線性或非線性過程中獲得廣泛應用［5］。

根據經驗，蒸汽開度變化與相應漂白塔上部溫度變化可近似表示為一階滯后環節蒸汽流量對象可近似表示為為更好利用最小二乘法辨識各參數對象，先去除滯后環節。

對一階無滯后環節過程，其數學模型為:

上述一階微分方程可近似表示為如下差分方程:

式中，KP為過程放大系數，TP為過程時間常數，k為數據采樣的次數，Ts為數據的采樣時間周期。

在第k次采樣時間t=kT，式(1)可近似寫成:

簡化式(3)可得:

式(4)為一階過程的動態差分動態模型。它表明過程在本次(k)采樣時的輸出值y(k)可以用上次(k-1)采樣時刻的輸入值x(k-1)和輸出值y(k-1)求得。式中，a、b是模型參數，與過程的放大系數KP、過程時間常數TP和采樣時間周期Ts有關。

因此，記錄各個采樣周期的輸入值x和輸出值y，然后用最小二乘法所預測數據進行回歸，求出差分模型中的最佳參數值。最佳參數值判斷標準是所求得差分方程的均方差為極小值。即先求出均方誤差:

然后，對a、b分別求偏導數，便可得到a、b，從而可以進一步得到模型參數。

通過實驗并對模型進行辨識，得到:

2 漂白過程溫度控制系統

2.1 被控變量和系統結構

為解決漂白過程容積過大造成的大滯后，采用串級控制系統結構。由于蒸汽流量波動是塔內溫度的主要干擾因素，故將蒸汽流量作為副控變量，引入副回路來提高控制系統抗干擾能力。主控變量為漂白塔上部溫度。主控制器選用模糊控制器，根據對象特性在線整定PID參數;副控制器采用比例控制器，加快系統響應速度。主副控制器分別為Smith預估器補償后的模糊PID控制器和純比例控制器，系統結構圖如圖1所示。

2.2 Smith預估器設計

圖1對應的控制系統方塊圖如圖2所示。圖2中的Gc2(s)為蒸汽流量調節器傳遞函數，G2(s)e-τ2s為副回路蒸汽流量對象傳遞函數，模糊PID控制器作為主調節器，其等效傳遞函數設為Gc1(s)，Gc(s)為主回路漂白塔上部對象傳遞函數，G2(s)(1-e-τ2s)和G0(s)(1-e-τ2s)分別為內外回路 Smith 預估器［6-7］。

其中，

副回路等效傳遞函數為:

其特征方程為:

可以看出，在蒸汽流量對象和漂白塔頂部溫度對象模型精確的情況下，副回路特征方程式中不包含純滯后項，從而消除了純滯后對副回路的影響。同理，驗證了前面給出的數學模型可以消除整個系統的滯后環節，整個系統特征方程為:

因此，純滯后特性不影響系統的穩定性。

2.3 溫度模糊控制器設計

2.3.1 模糊PID結構和論域設置

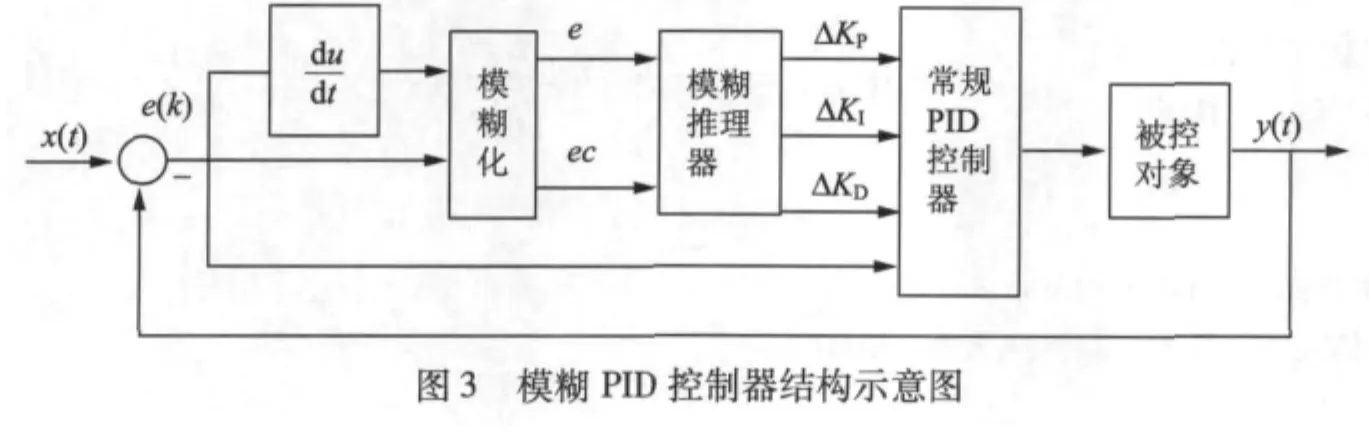
圖3給出了模糊PID控制器的原理框圖。該模糊控制器采用雙輸入、三輸出的結構，輸入為參數誤差e和誤差變化率ec，輸出分別為PID參數的變化量 ΔKP、ΔKI、ΔKD［8］。系統輸入輸出模糊集均為 {負大，負中，負小，零，正小，正中，正大}，記為 {NB，NM，NS， Z，PS， PM，PB}，將參數誤差 e論域設置為{-6，6}、ec論域設置為 {-0.18，0.18}、ΔKP論域設置為 {-0.03，0.03}、ΔKI論域設置為 {-3，3}、ΔKD論域設置為 {-0.9，0.9}。按經驗所有變量隸屬度函數均選為三角函數，均采用Mamdani決策法，解模糊采用centroid重心法，并在輸入輸出端分別添加量化因子，以便于對參數進行單獨調整。

2.3.2 模糊控制規則

模糊控制根據對象狀態實時調整參數，調整規則主要依據專家經驗和相關知識等，主要依據以下幾方面:

(1)在系統響應初始階段，此時誤差e較大，為了加快系統響應速度，應設定較大的KP來消除誤差;同時，該階段誤差變化率ec相當大，KD應取很小，防止積分飽和;為了防止系統超調過大，KI取值應較小。

(2)當誤差減小到中等大小時，系統主要任務是控制超調量，此時應對KP進行削減，同時增大積分系數KI，適量增大微分系數KD。

(3)系統趨于穩定時，誤差較小，KP取值應增大一些，提高系統響應速度。為了消除系統穩態誤差，KI的取值應適當，KD的取值則是為了避免產生振蕩。ec的絕對值較大時，取較小的KD;ec較小時，取較大的KD。根據以上規則，可以得到KP、KI、KD的模糊規則表(見表1～表3)。

表1 KP模糊控制規則表

表2 KI模糊控制規則表

表3 KD模糊控制規則表

模糊PID控制器調整PID參數計算為:

3 仿真分析

取式(6)中的模型作為仿真對象，選取適當的PID參數作為模糊控制器初始值，同時選取響應的量化因子。在模糊推理器Rules Editor窗口中，根據模糊規則，向表1～表3輸入各條控制規則。

If(e is NB)and(ec is NB)

then(KPis PB)(KIis NB)(KDis PS)

PID參數調整方式如式(11)～式(13)所示。建立的Simulink環境下仿真模型如圖4所示。

3.1 模型參數匹配時

在模型參數完全匹配情況下，t=0時，針對漂白塔上部溫度對象加入階躍擾動，完全穩定后對副回路蒸汽流量回路加入擾動，改進控制方案和單回路PID控制方案響應曲線如圖5所示。

3.2 模型參數失配時

當被控對象數學模型參數發生變化時，控制方案不變，即Smith預估器參數不變，而溫度對象和蒸汽流量對象參數均發生改變，改變后的模型設為和，同樣加入階躍擾動，并在系統穩定后對副回路加入擾動，改進控制方案和單回路PID控制方案響應曲線如圖6所示。

仿真結果表明，改進后的漂白溫度控制系統采用串級控制策略，并在主副回路分別進行Smith預估補償，有效地解決了漂白過程容積過大造成的大滯后問題，系統超調量大大減小，調節時間縮短。同時，在模型參數失配時，系統仍保持了很好的魯棒性，克服了Smith預估器對模型要求精確的缺點。

圖4 改進漂白溫度串級控制仿真模型

圖7 漂白塔上部溫度控制曲線

4 工業實際應用

本研究設計的控制系統已成功應用到山東某中型造紙廠漂白工段。系統使用西門子S7-300系列PLC，采用其本身提供的位置式輸出PID函數功能模塊FB41的接口參數，其變成原理基于位置式PID算法，程序中對 FB41的接口參數 I_Se1(積分選擇)及D_Se1(微分選擇)采用臨時變量動態賦值，DB11為FB41對應于漂白塔上部溫度控制的背景數據塊。誤差e和誤差變化率ec分別根據模糊規則表得到相應的數值，然后進行存儲，從而可通過查表法在線調整PID參數。

系統運行半年來溫度波動≤0.3℃，達到了很好的控制效果(見圖7)。

5 結論

針對紙漿漂白過程容積過大造成的大滯后、大慣性及蒸汽流量時變等問題，本研究對單回路漂白塔溫度控制系統進行改進，加入蒸汽流量副回路，使用模糊PID控制器作為主控制器，同時對主副回路分別設計了Smith預估器。仿真結果表明，改進后的控制系統有效解決了系統大時滯、大慣性及蒸汽流量時變的問題，同時，具有良好的魯棒性。最后，給出了工業應用中使用西門子S7-300系列PLC實現控制算法的方案，進一步體現了該控制方案的可行性和廣闊的應用前景。

［1］鄭恩讓，陳玉鐘，李英春，等.漂白過程溫度智能控制［J］.化工自動化及儀表，2002，29(4):21.

［2］唐德翠，甑任賀.單神經元自適應PID在漂白溫度控制中的應用［J］.廣東技術師范學院學報，2007(10):4.

［3］侯勇嚴，郭文強，黨宏社.基于IGA的漂白過程溫度優化控制［J］.微計算機信息，2009，25(11):68.

［4］劉煥彬，朱學峰.制漿造紙過程自動測量與控制［M］.北京:中國輕工業出版社，2009:268.

［5］張 虎，李正熙，童朝南.基于遞推最小二乘算法的感應電動機參數離線辨識［J］.中國電機工程學報，2011，31(18):79.

［6］劉寅東.基于兩級Smith預估的純滯后系統串級模糊控制仿真［J］.東北電力大學學報，2012，32(3):47.

［7］王 艦，強文義，麻 亮，等.一種改進的模糊 Smith預估器［J］.控制工程，2005，12(4):332.

［8］林 屹，葉小嶺.模糊自校正PID液位串級控制系統設計與仿真［J］.實驗室研究與探索，2010，29(3):17.