月基差分VLBI定位及參數精度探討

易 慧，黨亞民，魏二虎，嚴 韋，李 冠

（1.中國測繪科學研究院，北京 100830；2.武漢大學 測繪學院，武漢 430079；3.中國科學院 國家天文臺，北京 100012；4.北京城建勘測設計研究院有限責任公司，北京 100101）

1 前言

“嫦娥一號”圓滿完成了 “繞月”任務，近日，“嫦娥二號”成功對小行星 “戰神”進行了首次近距離探測，為 “嫦娥三號”的 “落月”任務打好了基礎。甚長基線干涉測量（Very Long Baseline Interferometry，VLBI）作為一種射電干涉測量技術，是用于深空探測器定位的主要技術之一。基于月球探測器離地面較近的特點和差分VLBI技術可以消除部分非幾何延遲的優勢，本文采用差分VLBI技術對月球探測器進行觀測。

文獻 ［1］提出了一種新型的差分VLBI觀測模型，該模型包含觀測量所在參考系統的連接參數，為提高定位精度作出了一定的貢獻。為了提高定位精度，除了尋求合適可行的定位模型外，提高參考系統連接參數的精度也是主要途徑之一。因此，研究月球探測器的坐標參數精度與參考系統連接參數的精度之間的關系是必要的，本文重點探討五個重要的EOP參數對定位精度的影響。

基于以上研究現狀，本文采用月球探測器奔月段的差分VLBI觀測量和觀測模型［1］，分析了EOP參數對探測器坐標先驗誤差的靈敏度，模擬了差分VLBI觀測量；最后平差計算了坐標參數和EOP參數的驗后精度。

2 差分VLBI觀測模型

2.1 基本原理

VLBI技術的基本觀測量是時間延遲和時間延遲率。時間延遲定義為河外射電源發出的同一信號到達地面不同位置處兩臺射電望遠鏡的時間之差。差分VLBI的觀測量是時間延遲之差，是由人工射電源和河外射電源發出的兩個射電信號，分別到達地面不同位置處兩臺射電望遠鏡的時間差之差，即總時延，記為τ，其中人工射電源發射的信號到達地面兩臺射電望遠鏡的時間差記為τs，河外射電源發射的信號到達地面兩臺射電望遠鏡的時間差記為τQ。

河外射電源的選擇有一定的限制，要求其和人工射電源的瞬時位置在空間方向上盡可能靠近。一般情況下，對于單頻觀測，二者角距不大于1°［2］。

根據定義，總時延的表達式為

在實際的VLBI觀測中，τS和τQ都是無法直接測量出來的，觀測值中還是將不可避免的包含一些誤差，實際的總時延τ為

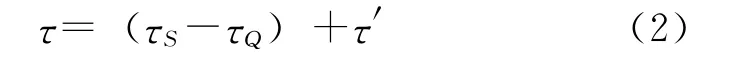
式中，τ′為總時延誤差。由于人工射電源和河外射電源的角位置非常靠近，由電離層、對流層等傳輸介質引起的時延誤差、時鐘同步誤差、測量設備群時延誤差可以有效的消除，τ′即為消除這些非幾何延遲后兩者共同的時延誤差。

由人工射電源發射的信號頻率是已知且可控制的。差分觀測具備以下優勢：①河外射電源的位置已知；②可消除部分非幾何延遲。這些對提高探測器的定位精度都是很有利的因素。故本文采用差分VLBI技術對月球探測器進行定位觀測。

2.2 觀測模型

圖1為月球探測器的差分VLBI觀測示意圖。

其中，記地面兩臺射電望遠鏡的位置為O1（X1，Y1，Z1）和O2（X2，Y2，Z2），月球探測器的位置為O（X，Y，Z），河外射電源為S。

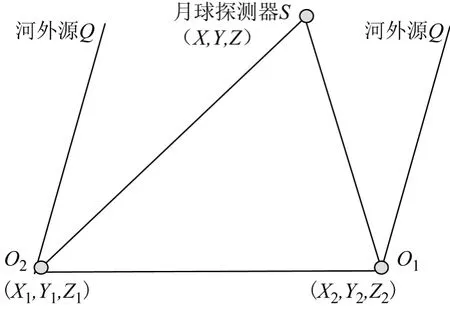
圖1 月球探測器的差分VLBI觀測原理圖

遵循平行四邊形法則［3］，結合一定的數學處理方法，奔月段具體模型為

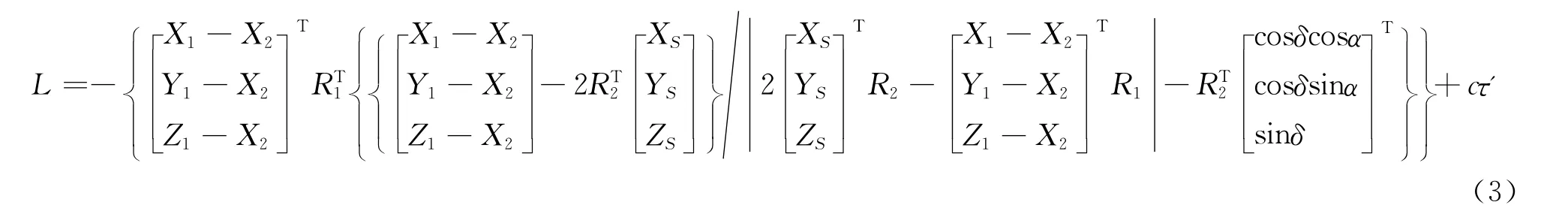
式中，（X1，Y1，Z1）和（X2，Y2，Z2）為地心地固坐標系中的兩個地面VLBI測站坐標，（XS，YS，ZS）為J2000.0地心慣性坐標系下的月球探測器坐標，α、β為J2000.0地心慣性坐標系下射電源的赤經赤緯，R1為地心地固坐標系到地心天球坐標系的旋轉矩陣，R2為地心慣性坐標系到地心天球坐標系的旋轉矩陣。

3 實驗

3.1 實驗條件的建立

本文以 “嫦娥”一號奔月段為例，該軌道段的運行時間是從2007年10月31日至2007年11月5日，為了讓地面站對探測器可見，需要進行探測器與地面站之間的可見性檢查，這個過程主要是在軟件中進行的。在地面上分布相當數量的測站，并選取2007年11月4日至11月5日作為檢查時段，以獲取探測器與測站之間的觀測時段數據。為獲取各個測站在該天內對探測器衛星的觀測情況并從中選擇具有共同觀測時段的測站，從而最后確定觀測時段。選取的原則是選擇盡可能多的具有相同觀測時段的測站以及盡可能長的時間段。

奔月段模型中的參數很多，根據需要本文只探討月球探測器的3個坐標參數和5個EOP參數，為了有足夠的多余觀測量，僅僅利用我國4個VLBI測站是不足以實現實時解算的，且又要考慮到全球實際的測站分布情況，因此需要對這些實際情況進行綜合考慮。

通過具體實驗，本文選擇的具體歷元時間為2007年11月4日凌晨02：00：00－03：00：00，為了使時間延遲數據保持良好的同步性，歷元間隔定為1s。本文最后選擇了17個測站，其中北半球13 個：BANDRY，BEIJING，KASHI，KUN－MING METSAHOVNYALES20ONSALA60，SHANGHAI，SVETLOE，TSUKUB32，URUM，WETTZELL，ZELENCHK，南半球4個： HRTRAO，HOBART26，PERTH－2，SYOWA。中國的四個VLBI測站都在其中。

根據差分VLBI的觀測原理可知射電源與月球探測器方向的一致程度一定程度上決定了月球探測器的定位精度。這里根據月球探測器的平均方向來選取臨近的射電源。探測器平均方向的計算方法為：取一定間隔的月球探測器的近似直角坐標平均值，然后轉換為大地坐標，最后轉換為赤經赤緯坐標作為選取射電源位置的參考值。

通過計算，符合條件的射電源的位置如表1所示。

關于EOP參數的近似值，則選用IERS于2007年11月4日所提供的數據（38.273mas，192.160mas，－215.7219ms，－63.694mas，－4.338mas）［4］。

3.2 實驗分析

3.2.1 數學模型

由于僅討論EOP參數的方差估計，因此將參數x分為兩部分，即 EOP（xp，yp，UT，Δψ，Δε）參數作為第一部分（x1），月球探測器的坐標參數作為第二部分（x2），這樣觀測方程可以寫成

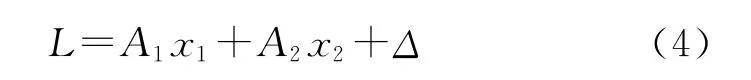
式中，A1為x1的偏導數，A2為x2的偏導數。考慮x2的先驗信息，設其先驗權證為P2，則有以下隨機模型

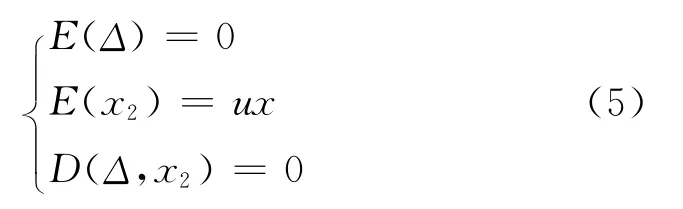
根據最小二乘配置原理，可以寫出法方程：

其中

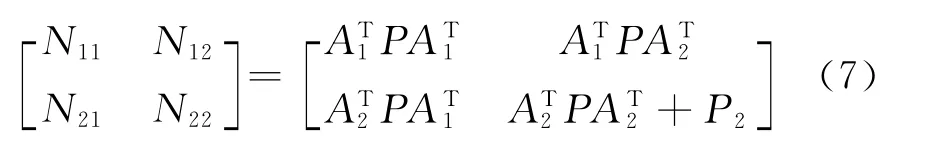
對N陣求逆，并由誤差傳播律得到EOP參數的方差陣

式中

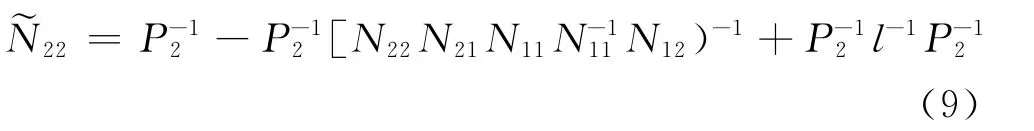
將式（9）代入式（8）可得到x1的方差陣為

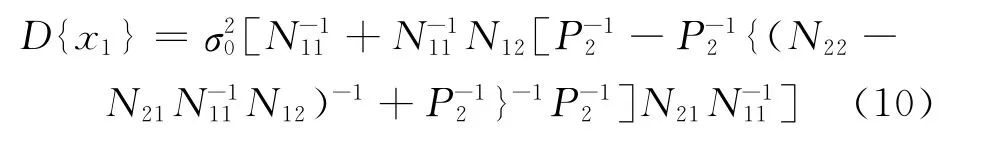
本文在以上觀測條件的基礎上，模擬新的參數近似值，形成系數矩陣A，組成法方程系數矩陣，并給探測器坐標參數賦予不同的先驗誤差信息，研究其對待估參數EOP參數精度的影響趨勢。

3.2.2 探測器坐標先驗誤差的確定

對于1mm／km（比例誤差）的月球探測器軌道，由 “嫦娥”一號探測器公布的參數可以計算得遠地點的地心半徑矢量大約為3.96×105km，相應的徑向誤差給出為：

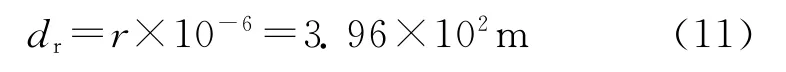
假設x，y和z的誤差相等，進而由式（11）可以得到，在比例誤差為1mm／km的情況下探測器坐標的誤差約為200m。為了分析月球探測器坐標的誤差對估計的EOP參數精度的影響趨勢，對探測器坐標賦予了0.001m，0.01m，0.1m，1m，10m和100m的先驗點位誤差。并由此計算EOP參數的標準差。

對以上坐標所賦予的先驗誤差，以目前的定位技術，被認為是合理的，根據上節的數學模型和以上設計的情況編程進行了數值實驗，實驗結果如表2所示。

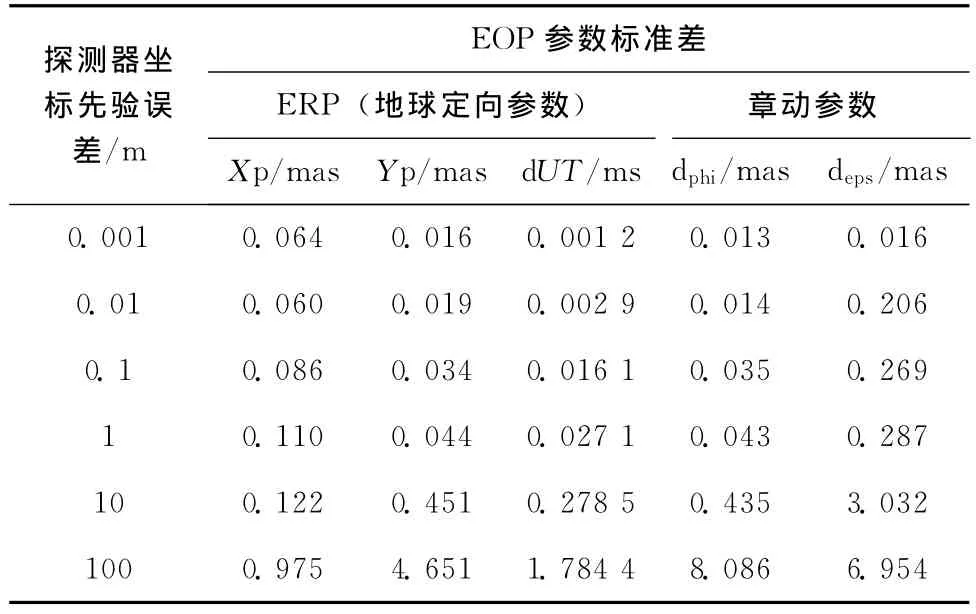
表2 不同探測器坐標誤差計算的EOP參數精度

表2、圖2、圖3及圖4給出了月球探測器坐標誤差對ERP（地球自轉參數）和章動參數的影響趨勢。當月球探測器坐標的先驗誤差小于1m時，表2中顯示的EOP參數的精度基本沒有變化趨勢，并且和IVS官方網站上公布的EOP參數精度基本在一個量級上；當探測器的先驗誤差在1m－10m時，EOP參數精度和IVS網站上的精度高出了一個量級；當大于10m后，EOP參數精度的數值飆升，即EOP參數的精度開始顯著下降，精度出現嚴重偏差。

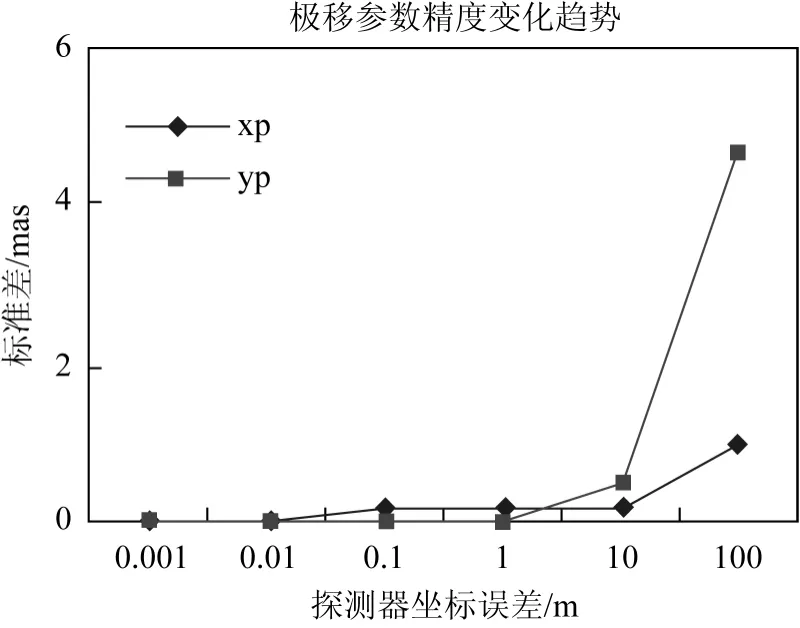
圖2 探測器坐標誤差對極移參數精度的影響

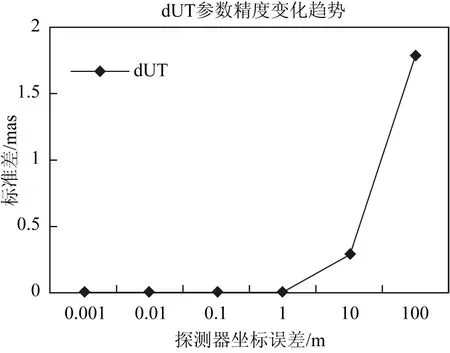
圖3 探測器坐標誤差對dUT參數精度的影響

圖4 探測器坐標誤差對章動參數精度的影響

因此可知，要想得到較好的EOP參數的解算結果，探測器坐標的先驗誤差應設在1m之內，這是個分界值。

3.2.3 模擬觀測量

在得到測站的地心地固坐標系下的坐標以及月球探測器的實時坐標之后，就可以進行觀測值的模擬，模擬主要包括模擬幾何延遲和非幾何延遲，幾何延遲可以根據確定的數學公式，即先求出月球探測器到兩測站的距離差，再利用常規VLBI的原理公式求出兩測站對射電源的延遲觀測量，進而實現差分VLBI觀測量幾何延遲部分的模擬，模擬的重點在于非幾何延遲的模擬。

在兩個同時觀測的目標的非幾何延遲中，有一些量是相同的，如：鐘差、儀器延遲等。另一些則和目標在空間的方向有關，如：電離層延遲、對流層延遲等［5］。由于時間關系，本文僅在觀測量中加入了兩項誤差源：對流層延遲誤差殘差及隨機誤差。

本文依據hopfield模型［6］，并利用觀測站的每一個歷元的氣象數據，計算了要添加到幾何延遲中的對流層路徑影響，從而模擬出了對流層延遲量。雖然有模型可以算出對流層延遲的值，但是并不能完全消除這種誤差，而且對流層模型的殘差誤差大概為總誤差的2%，所以在模擬觀測量的過程中，本文通過已有的對流層算法程序，采用了將2%的對流層延遲值來模擬對流層延遲誤差的殘差［7］。

在真實的觀測量中常常帶有隨機誤差，由N.Tamin編寫的子程序RANDOM已經用于模擬觀測量程序中：利用隨機數乘上觀測量的期望標準偏差σ，處于－3σ與＋3σ之間，便產生了隨機噪聲。將其添加到時間延遲中。在本文中，VLBI時間延遲觀測量的期望標準偏差σ取值為0.5μs，利用上述方法來產生隨機誤差，使模擬出來的觀測量與其中包含的一些幾何及誤差模型的聯系變弱，因而具有更強的隨機性［8］。

3.2.4 平差計算

根據前面所討論的先驗精度，月球探測器的先驗誤差只有達到了米級才能更好的應用于EOP的參數解算。本實驗將月球探測器坐標的先驗精度設定為1m，同時利用上一節中所得到的模擬觀測量來對2007年11月4日02：00－03：00間的3 601個歷元的數據進行平差解算，得到EOP參數的結果及解算精度如表3所示。

表3 EOP參數的解算結果及精度

從表3中可以看出，實驗解算的EOP參數精度和CONT08數據解算的EOP參數精度雖然在一個量級上，但基本上都略低于它，這是因為CONT08數據是用對射電源進行VLBI觀測得來的結果，而本次實驗則利用的是對有限距離探測器進行觀測得來的結果。這些一方面說明了采用此模型解算EOP參數是可行并且成功的；另一方面則用數據說明了與觀測遙遠的河外射電源相比，利用觀測有限距離的探測器來進行EOP參數的解算是有不足之處的。

月球探測器坐標的解算精度，如下表4所示。

表4 月球探測器坐標解算精度（m）

采用VLBI技術對衛星定位的精度是幾mas到幾十mas［9］，換算成距離精度是幾米到十幾米。從表4可以看出，采用差分VLBI技術對探測器進行定位觀測的精度可以達到米級甚至亞米級。

模擬計算結果表明，對有限距離的探測器進行定位觀測，采用差分VLBI技術觀測比VLBI技術精度要高。這也驗證了采用差分VLBI技術對月球探測器進行定位觀測的優勢，即可以消除部分非幾何延遲誤差，進而可以提高定位精度。

4 結束語

本文在瞬時地心天球坐標系下以 “嫦娥”一號奔月段的數據為例進行了模擬計算。通過分析EOP參數的精度對探測器坐標先驗誤差的靈敏度，若要得到理想的EOP參數的解算結果，探測器坐標的先驗誤差應設在1m之內。然后采用模擬觀測量平差計算了探測器的坐標參數的驗后精度。模擬計算結果表明，采用差分VLBI技術對探測器進行定位觀測的精度可以達到米級甚至亞米級，EOP參數的精度可以達到10－2mas或ms。

［1］ 魏二虎，易 慧，劉經南.月球探測器差分VLBI觀測量的模型及可估計參數研究［J］.測繪通報，2011（1）：1－3.

［2］ 舒逢春，張秀忠，鄭為民.地球同步衛星的 VLBI觀測［J］.中國科學院上海天文臺年刊，2003，24（00）：105－111.

［3］ SEKIDO M，TOSHIO F.Relativistic VLBI Delay Model for Finite Distance Radio Source［C］／／SansòF.A Window on the Future of Geodesy.Berlin：Springer－Verlag，2005：141－145.

［4］ International Earth Rotation ＆ Reference Systems Service.［EB／OL］.［2012－11－12］http：／／hpiers.obspm.fr／.

［5］ 王 靜.航天器較差VLBI測量的一種實現方案［D］.上海：中國科學院上海天文臺，2007.

［6］ 李征航，黃勁松.GPS測量與數據處理［M］.武漢：武漢大學出版社，2005.

［7］ 魏二虎.我國空間VLBI系統的有關設計和模擬計算研究［D］.武漢：武漢大學測繪學院，2006.

［8］ 喬書波，李金嶺，孫付平.VLBI探月衛星定位中的應用分析［J］.測繪科學，2007，32（3）：262－268.

［9］ áDáM J.Estimability of Geodetic Parameters from Space VLBI Observables［R］.Ohio：The Ohio State University，1990.