抗差推估GNSS水準高程擬合方法研究

郭范春

（遼寧省測繪產品質量監督檢驗站，遼寧 沈陽 110034）

1 概述

GNSS水準高程擬合所用的數據不可避免的包含一定的誤差，誤差產生的原因是多方面的同時也包含多方面的粗差。清楚認識誤差對擬合結果的影響規律，找到探測粗差的方法，采取必要措施將其削弱或消除，提高成果的可靠性和精確性十分必要。

目前高程擬合技術主要有整體擬合、隨機插值、分區擬合、逐點內插等方法，這些方法對待定點周圍的參考點質量和數量有嚴格的要求。由于參考點大地高、待定點大地高及其平面坐標這些數據本身的誤差大小不盡一致，已知數據由于非同一年代實測、非同網平差或等諸多原因，致使擬合時在局部范圍內這些數據不能滿足要求或兼容，加之有些測區范圍較大，或地形起伏較大，這種情況下就對高程擬合結果影響更為嚴重［1－6］。某些數據對于待定點擬合影響較大，變成了粗差，必須剔除或削弱這些點對周圍待定點的影響。為此，論文提出抗差推估方法結合其它擬合方法進行GNSS水準擬合計算，從而提高擬合結果的質量和可靠性。

2 抗差推估GNSS水準高程擬合

2.1 最小二乘推估擬合模型

設GNSS點高程異常ζ與平面坐標（x，y）有如下式所示的函數關系

式中，f（x，y）為ζ中趨勢值，ε為誤差。

在GNSS水準高程擬合時，按常規擬合方法，則上式函數關系的矩陣形式為

因為對于每一個點都可以列立這樣的方程，在∑ε2＝min條件下，利用最小二乘理論解出式（2）方程組，再按式（1）求出待求點的ζ。

由大地高H（GNSS測得）與正常高Hr以及高程異常ζ的關系式H＝Hr＋ζ，從而可以求出正常高Hr。

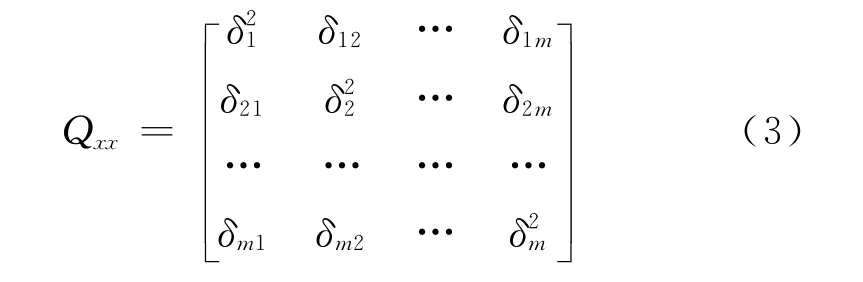
高程異常是一隨機變量，若能知道觀測區域內高程異常分布的隨機統計信息，即已知參考點間高程異常的方差－協方差陣

以及參考點與待定點間高程異常的方差－協方差陣

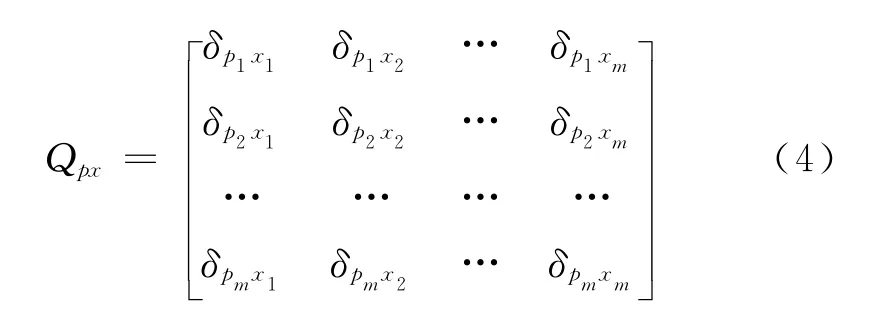
就可采用最小二乘推估法確定其趨勢值。其推估式為

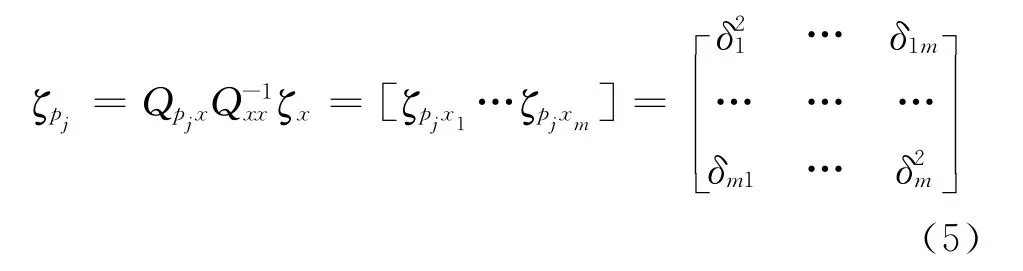
式（3）、式（4）及式（5）中，ζxi（i＝1，…，m）為m個己知點上的高程異常，ζpj（j＝1，…，n）為n個待定點上的高程異常，δi2、δij為ζxi的方差、ζxi與ζxj間的協方差，δpjxi為ζpj與ζxi間的協方差。Qxx、Qpx的確定借助于觀測區域內高程異常協方差函數而建立。

如果能確定描述高程異常隨機信息的協方差函數，最小二乘推估擬合就是首選方法，比一般擬合法要精確，而且已知點的分布沒有具體要求。但要建立較為精確的協方差函數比較困難。為此采用抗差推估方法進行高程擬合。

2.1 抗差推估擬合

抗差推估擬合法是在原最小二乘擬合推估法的基礎上發展起來的一種選權迭代法［9］。它通過驗后方差估計求出觀測值的驗后方差。然后利用方差檢驗找出方差異常大的觀測值，根據方差與權成反比的關系，給它一個相應小的權，進行下一步的迭代平差計算，重復以上過程，使含有粗差的觀測值的權越來越小甚至于等于0，從而使其對平差結果的影響很小，在某種意義上說，當觀測值的權很小或者等于0時，也就相當于從觀測序列中剔除了該觀測值，因此在迭代的過程中，逐步發現粗差并將其 “剔除”。對于GPS高程擬合推估，具體的計算步驟是首先進行最小二乘平差，即傳統 GNSS高程擬合［10－12］。在本文研究中，式（1）的數學模型代換的是多項式曲面擬合模型，如下式

第一次抗差時，初權為1，然后根據式（7）進行驗后方差估計：

其中ri為多余觀測分量，ri＝（Qvvp）ii。

根據驗后方差計算等價權，計算等價權的方法很多，如Huber函數：

c0一般取1.5～2.0，σ0是單位權標準差。

或者取指數函數為

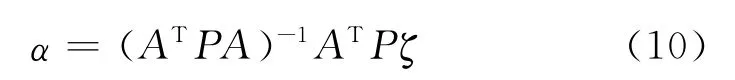
重復以上步驟，隨著迭代次數的增加，如果某一觀測值的權變得越來越小甚至為0，這就說明該觀測值含有粗差，或者與其它觀測值不相容，不能納入己知點列用于計算擬合函數系數；實際上，當權降低到很小時，其對平差結果的影響也就很小，甚至沒有影響，從而計算結果抗差化。

迭代次數的增加，并非無限次循環下去，這里給出判定標準。以多項式相關平面數學模型說明，如式（11）所示

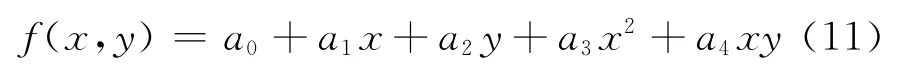
一般情況下，設參考點的數目為n（n大于5），所以要進行最小二乘法解算。判定的第一個標準是，在迭代到k次時，根據精度評定，可以計算出中誤差σ0，如果

式中μ為工程精度要求，σ0為擬合后的參考點精度。式（12）成立，則表明抗差滿足要求，迭代完畢。其二，當在迭代到k次時，隨著權不斷變小，某些權可能為0，如果此時權不為0的參考點的個數：

即n′小于式（11）所示方程式中的系數個數，則方程不可解。這時可以降低工程精度的要求，重新解算。

具體算法實現時，可以在成果文件中查看每一次迭代的結果，包括權、誤差、精度和標準差，這樣就可以根據具體的要求，考察每一個參考點的精確性和可靠性，以作為排除點的依據。

3 工程應用及分析

為了考察抗差推估GNSS水準高程擬合方法的可行性和準確性，本文采用某GPS高程控制網進行計算分析。該GPS高程控制網所覆蓋的區域東西長12km，南北長18km，總面積約為214km2。圖1為全部GPS點平面分布情況，圖2為27個GPS試驗點分布情況圖。GPS測點高程異常最大值為6.816m，最小值為6.410m；同時，水準高差最大值為6.115m，最小值為3.376m。

3.1 一次抗差推估結果分析

根據前面的理論和通過編程實現了相關平面、二次曲面、三次曲面三種方法抗差推估GNSS水準高程擬合。表1給出了全部控制點一次抗差推估的結果，其中差值是擬合后的GPS水準高與幾何水準高的之差。

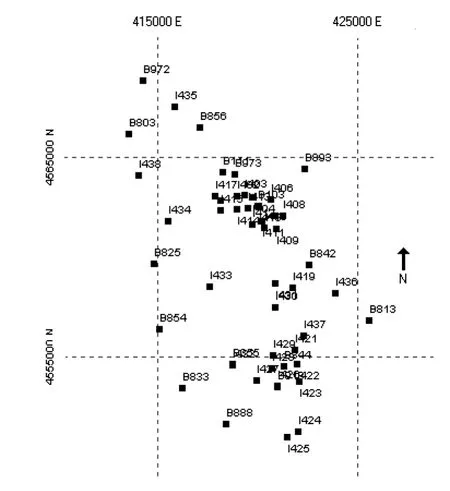
圖1 全部GPS點平面分布圖

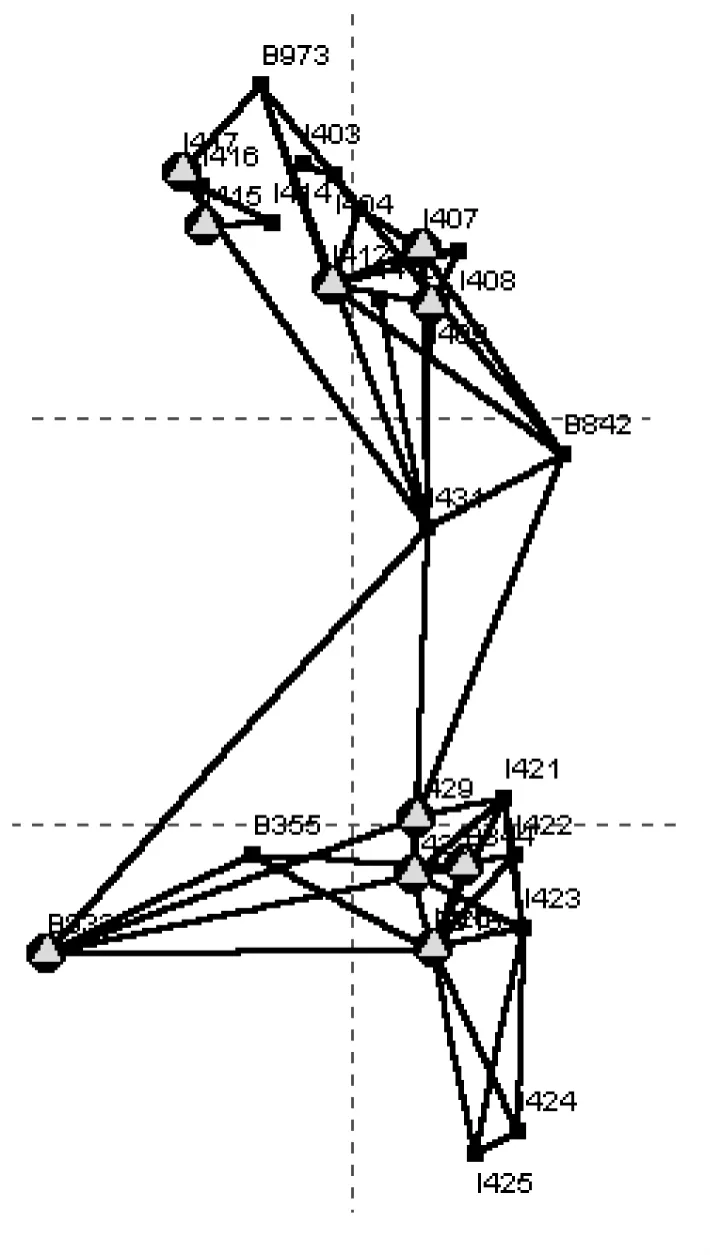
圖2 27個GPS試驗點分布圖

由表1可以看出，二次曲面抗差結果符合點較少，且接近0的點較多。但是從超出誤差限的個數統計來看，相關平面不符合點個數最多，二次曲面卻最少。而且發現，某些點經過抗差后，三種結果有不同的差值，例如B972、B842。對此作為研究，將它們保留。由多項式的特性，再根據該市地勢平坦特點，作為檢測，綜合分析三種抗差推估結果，將誤差超過5.0cm或權接近0的點認為含有粗差，剔除掉。由此找出14個點符合要求，剔除掉后剩下37個點符合要求。

3.2 二次抗差推估結果分析

在以上計算分析的基礎上，進行二次抗差推估，其結果見表2。表2列出了相關平面和二次曲面抗差的結果。根據第一次剔除誤差的方法，綜合分析，再次剔除粗差點10個，這樣剩下27個符合要求，它們也是以后進行擬合分析的試驗點，分布如圖2所示。

3.3 最終結果分析

本文再將控制點權接近1或誤差在1cm以下，結合圖形分布選擇以下首級控制點，它們為：B344、B833、I407、I409、I412、I415、I417、I426、I429、I428共10個點，其余17個點則作為待定點（擬合點）。進行了計算。

表1 三種整體抗差推估方法比較

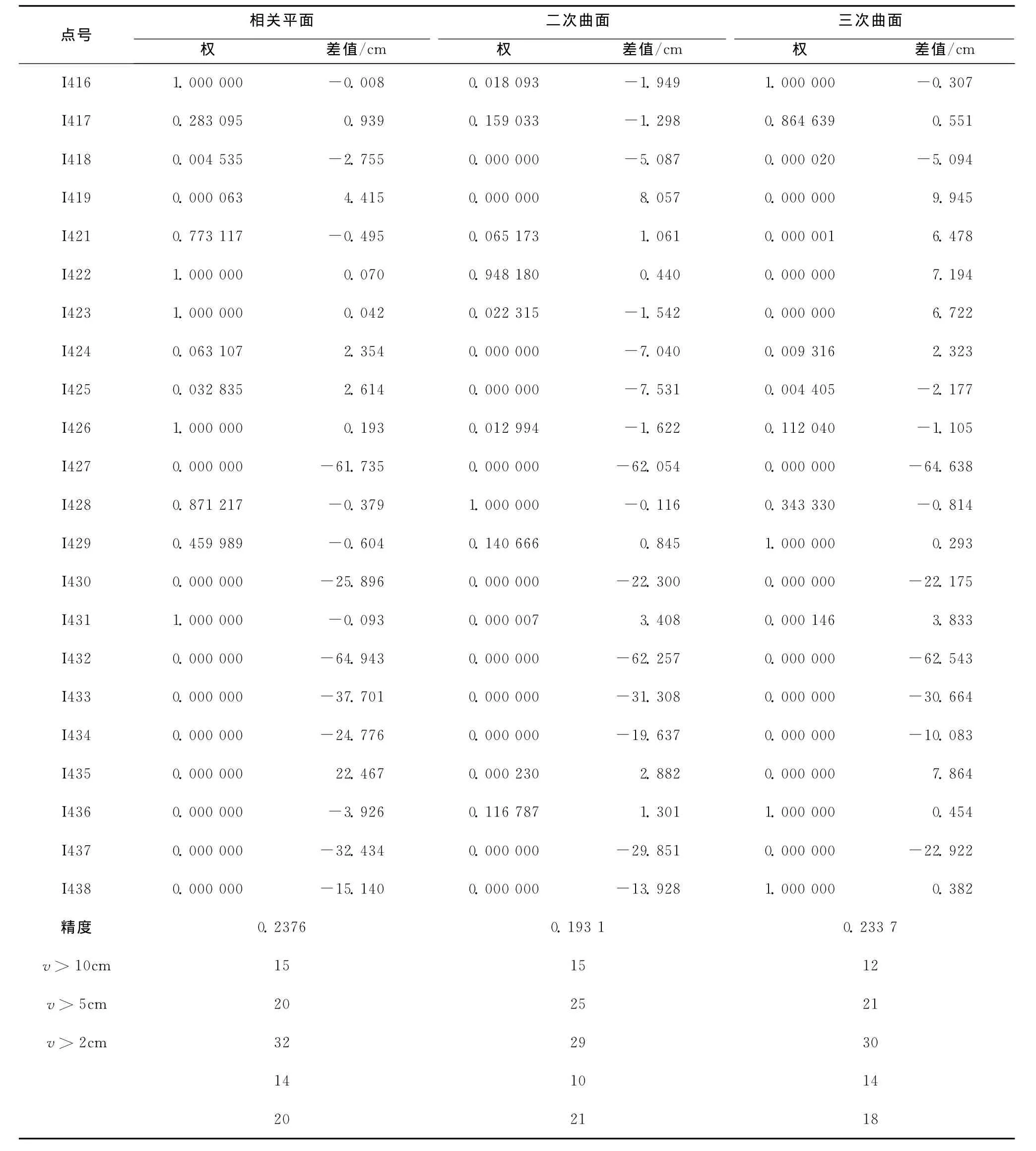
續表

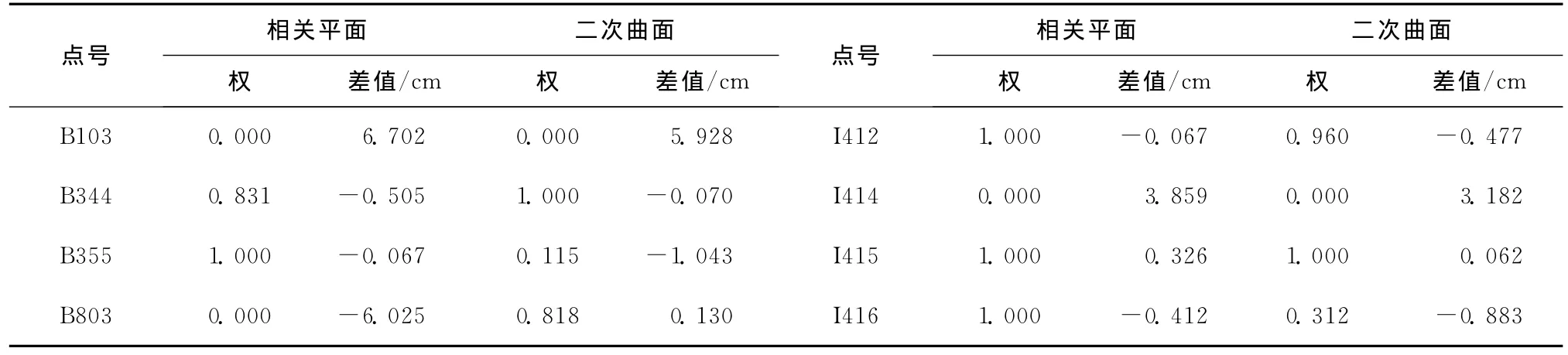
表2 二次整體抗差推估結果

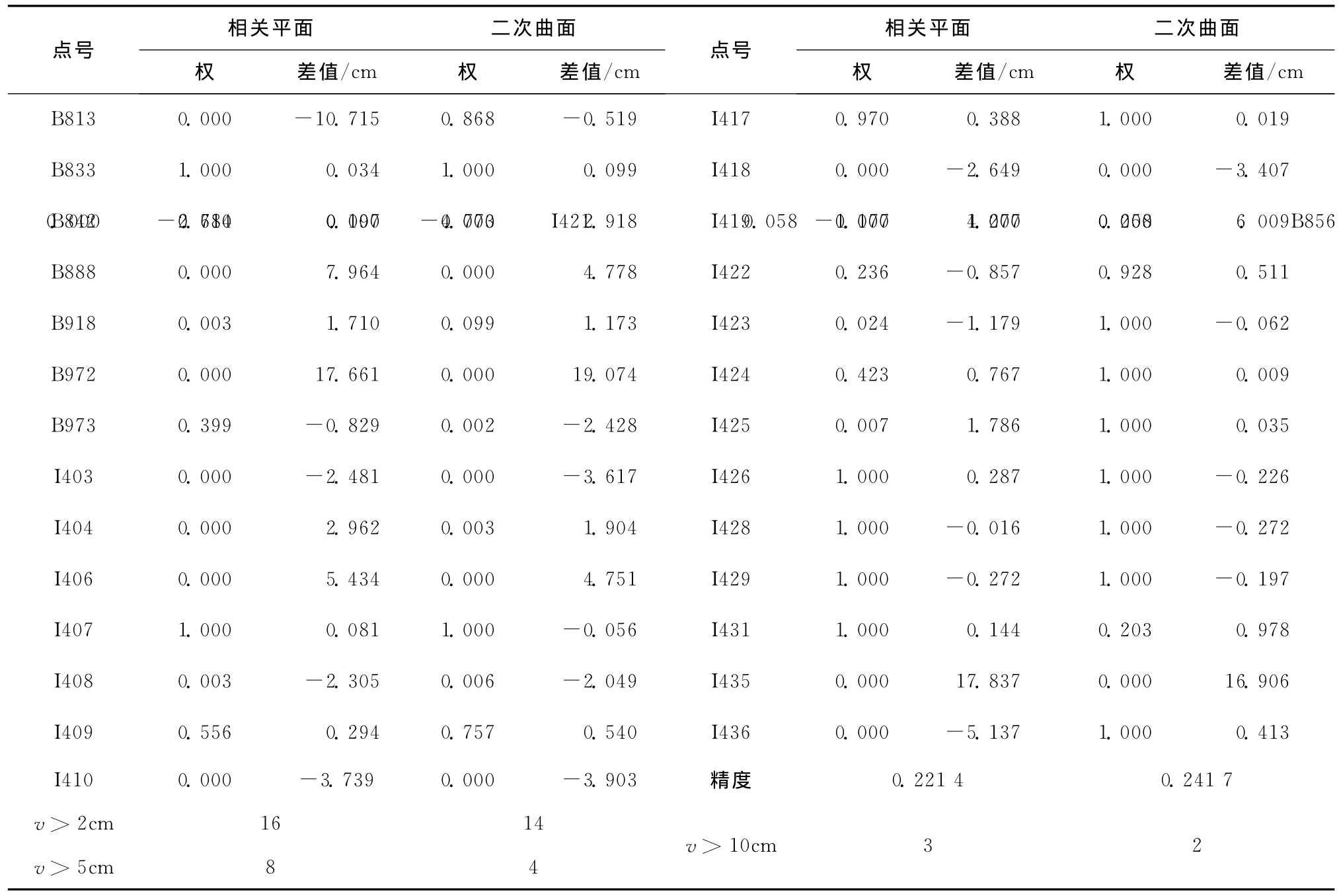
續表

4 結論

（1）在高程控制網中，已知高程點數目比較多，且分布情況不理想，在進行GPS水準高程擬合時，先進行抗差計算，剔除個別含有粗差的點能有效的提高高程擬合精度。

（2）在一定的條件下，二次曲面抗差的結果精度要好于相關平面與三次曲面抗差的結果精度，經過二次曲面抗差后符合要求的點數最多，說明二次曲面抗差模型的有效性比其它兩種模型要好。

（3）抗差模型的精度與點位分布有關系，個別含有粗差的點經過三種模型進行抗差計算后，結果各不相同，這要求在進行抗差計算時要結合多種模型進行比較分析，特別點要進行多次抗差計算。

［1］ 李德仁、袁修孝.誤差處理與可靠性理論［M］.武漢：武漢大學出版社，2002：235－294.

［2］ SHRESTHA R L，NAZIR A，DEWITT B A，etal.Surface Interpolation Techniques to Convert GPS Ellipsoid Heights to Elevations［J］.Surveying and Land Information Systems，1993，53（3）：133－144.

［3］ 李建成.最新中國陸地數字高程基準模型：重力似大地水準面CNGG2011［J］.測繪學報，2012，41（5）：651－660.

［4］ 蔣 濤.利用航空重力測量數據確定區域大地水準面［J］.測繪學報，2013，42（1）：152.

［5］ 李建成.我國現代高程測定關鍵技術若干問題的研究及進展［J］.武漢大學學報：信息科學版，2007，32（11）：980－987.

［6］ 馬洪濱，董仲宇.基于DEM與重力場模型的GPS水準高程處理方法研究［J］.武漢大學學報：信息科學版，2007，32（9）：767－769.

［7］ 章傳銀，黨亞民，柯寶貴，等.高精度海岸帶重力似大地水準面的若干問題討論［J］.測繪學報，2012，41（5）：709－714.

［8］ 陳俊勇，李建成，寧津生，等.全國及部分省市地區高精度、高分辨率大地水準面的研究及其實施［J］.武漢大學學報：信息科學版，2006，34（4）：283－288.

［9］ 馬洪濱，董仲宇.多面函數GPS水準高程擬合中光滑因子求定方法［J］.東北大學學報：自然科學版，2008，29（8）：1176－1178.

［10］ 陳俊勇，李健成，寧津生，等.我國大陸高精度、高分辨率大地水準面的研究和實施［J］.測繪學報，2001，30（2）：95－100.

［11］ 郭東美，許厚澤.應用GPS水準與重力數據聯合解算大地水準面［J］.武漢大學學報：信息科學版，2011，36（5）：621－624.

［12］ 申文斌，韓建成.利用新方法確定的30′×30′全球大地水準面模型及其精度評估［J］.武漢大學學報：信息科學版，2012，37（10）：1135－1139.