帶附加供料流和存在損耗的準理想級聯模型
謝全新,叢藝坤,邱志恒,趙文忠
(核工業理化工程研究院,天津 300180)
某些特殊同位素分離任務需要借助帶附加供料流的級聯來完成,比如乏燃料中回收鈾的再濃縮[1-2],原料昂貴的同位素混合物分離后貧料的再利用,以及某些分離過程對輕雜質的凈化等[3]。此外,在同位素分離過程中,可能存在工作物質的損耗[4-6]。當分離任務需要設計帶附加供料流級聯且同時存在工作物質的損耗時,級聯的計算將不同于普通級聯。
級聯的設計和優化通常以某種模型級聯為基礎,比如二元分離情況下的理想級聯[7],多元分離(或多組分同位素分離)情況下的Q級聯[8]和準理想級聯[9-11]。在實際級聯設計中,通常先通過理論計算設計出符合要求的級聯模型,然后在實際級聯建設中,使實際級聯的結構盡可能地靠近級聯模型。在文獻[12]中討論了帶附加流的Q級聯的計算方法,而帶附加流的準理想級聯的計算在文獻[13]中進行了探討,本研究將討論帶附加供料流并同時存在損耗的準理想級聯的數學模型。
1 級聯模型
級聯中物質輸運規律是級聯特性研究的基礎和前提。而物質輸運規律通常借助于合理的數學模型來描述。為使理論更具有一般性,對帶附加供料流同時存在工作物質損耗的多組分逆流型級聯進行研究,帶附加供料流并存在損耗的準理想級聯模型圖示于圖1。

圖1 帶附加供料流并存在損耗的準理想級聯模型圖Fig.1 Quasi-ideal cascade with an additional feed flow and losses of working substances
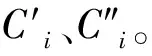
(1)
級的分流比θ(s)以及級的組分分流比φi(s)定義為:
(2)
定義變量gi(s)為第i組分在第s級的精料流與貧料流之比,即:
(3)
對于準理想級聯,φi(s)為常量,因而gi(s)也為常量,并可表示為[4,11,13-14]:
(4)
k是關鍵同位素的組分序數,αik、βik是第i、k兩種組分的精料相對分離系數與貧料相對分離系數,準理想級聯中αik、βik各級相等。
由(4)式可以得到:
(5)
qik是第i、k兩種組分的相對全分離系數。對于大多數基于分子動力學的分離方法,相對全分離系數qik可表示為[2, 4,10-11,13-16]:
qik=q0Mk-Mi
(6)
q0為基本全分離系數,Mk、Mi為k、i兩組分的相對分子質量。
另一個重要的概念是豐度比匹配級聯(matched abundance ratio cascade),簡稱M級聯或MARC[5-6, 10-11, 13-18]。它是準理想級聯的一種特殊情形,滿足在級的匯合點處被選定的兩組分(例如第n和k第組分)的相對豐度相等,可表示為:
(7)
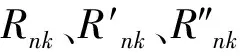
(8)
在這種情況下,gi可以用基本全分離系數q0以及組分相對分子質量來表達[ 4,10-11,13-16, 18]:
gi=q0M*-Mi
(9)
其中
(10)
假設損耗同時存在于各級的供料流,且工作物質的損耗量ΔLs正比于物質流量(見圖1),那么
ΔLs=yL(s)
(11)
其中y是損耗系數,在級聯各級中保持不變。
在穩態條件下,對于任意分離級s(s≠f)存在以下組分流守恒方程:
(12)
考慮到
(13)
方程(12)可整理為:
(14)
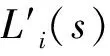
(15)
方程(14)是存在損耗的準理想級聯的組分流輸運方程,要研究這種級聯的分離特性,必須對級聯三個區段分別求解。
(16)
Ai、Bi為常數,由具體的邊界條件來確定,ω1i、ω2i是下面二次方程的解,
ωi2-(gi+1)(1+y)ω1+gi=0
(17)
即:
(18)
利用邊界條件(15)可以確定方程(14)在級聯各區段的解:
(19)
(20)
(21)
式(21)中的系數Ai、Bi可表達為:
(22)
(23)
利用方程(14)在級聯各區段的解(19)~(21)可進一步確定級聯精料組分豐度CiP、貧料組分豐度CiW與供料豐度CiF、CiE之間的關系:
(24)
(25)
其中
(26)
(27)
對式(19)、(20)和(21)在相應級聯段求和并利用(13)式可以得到級聯中總的物質流量LT:
(28)
其中
(29)
如果已知參量CiF、CiE、gi、N、f、l、E/F,由關系式(24)~(27)可以計算出級聯精料流和貧料流的相對流量P/F、W/F,精料流和貧料流中的組分豐度CiP、CiW。利用關系式(19)~(21),(1)~(3)以及(13)能確定級聯各級中物質流量L(s),Ci(s)組分豐度和級的分流比θ(s),由(28)式可計算級聯中的總物質流量LT。
2 理論應用
乏燃料中回收鈾的再利用能節省天然鈾資源。如果反應堆使用的是濃縮鈾(235U的豐度為3%~5%),從輕水堆乏燃料中回收的鈾(稱之為回收鈾)必須濃縮才能再利用。回收鈾中除含有235U和238U外,還含有一定量的232U、234U和236U。232U及其衰變產物具有輻射性,而236U能吸收中子,對燃料元件的燃耗深度產生負面影響[19-22]。因此在分離回收鈾的過程中,除了濃縮235U,凈化或者稀釋232U,同時還必須考慮因236U引起的燃耗深度損耗的補償問題[23]。
文獻[1-2]中結果表明,在所有可能用于濃縮回收鈾的單級聯方案中,最為有效的是利用帶附加供料流的級聯,天然鈾作主供料流,回收鈾作附加供料流。天然鈾和回收鈾的組分及其豐度列于表1。其中回收鈾的豐度為輕水反應堆VVER-440的堆后料經10年儲存期后的典型豐度。
下面將對這種級聯進行理論計算。基本全分離系數q0=1.062 7,因此235U和238U(即第3組分和第5組分)兩種組分的相對全分離系數q35=q0(238-235)=1.2。級聯總長度N=30級,主供料級為第13級。假設級聯為M級聯,兩種關鍵同位素取第3組分和第5組分,即在表達式(9)中n=3,k=5。計算結果示于圖2。

表1 天然鈾和回收鈾的組分及其豐度
圖2a對應附加供料級在第15級,而圖2b對應附加供料級在第25級。當主供料級在第13級,附加供料級在第15級時,損耗因子對235U在級聯精料中的豐度幾乎沒有影響,兩供料流的比值E/F對C3P的影響也不十分明顯。這主要是因為附加供料流在第15級時,附加流中235U的豐度與級聯中附加供料點處235U的豐度接近,減小了級聯中附加供料點的豐度混合損耗。雖然損耗因子在這種情況下對235U的精料豐度不產生實質性的影響,但是損耗因子的增加,將導致級聯中總的工作物質損耗的增加,也就是說,獲得單位重量指定豐度產品時,總的供料流量以及級聯的級間流量都將增加。這一方面會增加原料成本,另一方面不得不增加級聯分離器的總數。所以損耗的存在對同位素分離始終是一個不利因素。
圖2b表明,當附加供料級在第25級時,由于附加流中235U的豐度與級聯中附加供料點處235U的豐度差別較大,因而豐度混合損耗增加,這導致損耗因子y和兩供料流的比E/F的變化對235U的精料豐度產生實質性的影響,C3P隨y和E/F的增加而減小。

a——l=15; b——l=25圖2 產品豐度C3P與y以及E/F的關系a——l=15; b——l=25Fig.2 Dependences of the product abundance on and
3 結論
本研究建立了帶附加供料流且同時存在損耗的準理想級聯的數學模型。得到了計算該類級聯中相對產品流、相對貧料流、精料和貧料豐度以及級聯中的總物質流量的解析表達式。附加流中235U和238U兩組分的相對豐度與級聯中的這兩種組分的相對豐度接近時,損耗因子對235U的精料豐度影響最小,這可以作為選擇最佳附加供料位置的判據。
參考文獻:
[1]Sulaberidze GA, Borisevich VD, Quanxin XIE. On some separation problems on regenerated uranium application in the fuel cycle [C]// Proceedings of IX All-Russia (International) Scientific Conference, “Physical and Chemical Processes on Selection of Atoms and Molecules”, Russia: Zvenigorod, 2004: 70-77.
[2]Sulaberidze GA, Borisevich VD, Quanxin XIE. Study of regularities of stationary mass transfer in separating cascade for enrichment of regenerated uranium [J]. Engineering Physics, 2005, 3: 15 -19 (in Russian).
[3]賈興國,應純同,曾實. 附加供料離心凈化級聯的實現[J]. 清華大學學報(自然科學版), 2006, 46(3): 371-373.
Jia Xingguo, Ying Chuntong, Zeng Shi. Realization of centrifuge purge cascade with additional feed [J]. Journal of Tsinghua University (Sci & Tech), 2006, 46(3): 371-373.
[4]Sulaberidze GA, Quanxin XIE, Borisevich VD. On some properties of quasi-ideal cascades with losses at stages [J]. Ars Separatoria Acta, 2006, 4: 67-77.
[5]Quanxin XIE, Sulaberidze GA, Borisevich VD. Some properties of quasi-ideal cascades with losses at stages [C]// Proceedings of the XX International Symposium on Physoco-Chemical Methods of the Mixtures Separation, “Ars Separatoria 2005”, Poland:Szklarska Poreba, 2005: 205-207.
[6]Quanxin XIE, Borisevich VD, Potapov DV. Multicomponent isotope mixture separation in square cascade with losses of working substances [J]. Engineering Physics, 2006, 2: 30-34 (in Russian).
[7]Cohen K. The theory of isotope separation as applied to the large scale production of235U [M]. NY: Mc, Graw-hill Book Co. Ink., 1951.
[8]Kecherov RYA, Minenko VP. Theory of cascades for separatiing multicomponent isotope mixtures [J]. Atomic Energy, 1961, 3: 188-194 (in Russian).
[9]Baranov VYU. Isotopes: Properties, Production, Application [M]. 1st ed. Мoscow: IzDAT, 2000: 72-107 (in Russian).
[10]Quanxin XIE, Sulaberidze GA, Borisevich VD. Optimization of Model cascades for Multicomponent Isotope Mixtures [C]// Proceedings of XI All-Russia (International) Scientific Conference, “Physical and Chemical Processes on Selection of Atoms and Molecules”. Russian, 2006: 15-20.
[11]謝全新,李大勇,李文泊,等.多組份同位素分離級聯的優化[J]. 核科學與工程,2008, 1:86-91.
Quanxin XIE, Dayong LI, Wenbo LI, et al. Cascade optimization for multicomponent isotope separation [J]. Chinese Journal of Nuclear Science and Engineering, 2008, 1: 86-91.
[12]蔣同遠. 多組分同位素分離級聯計算 [J]. 清華大學學報(自然科學版), 1994, 34(S2): 54-62.
Tongyuan Jiang. A cascade analysis for multicomponent isotope separation[J]. Journal of Tsinghua University (Sci & Tech), 1994, 34(S2): 54-62.
[13]Sulaberidze GA, Borisevich VD, Quanxin XIE. Quasi-Ideal cascades with an additional flow for separation of multicomponent isotope mixtures [J]. Theoretical Foundations of Chemical Engineering, 2006, 40 (1): 7-16.
[14]Sulaberidze GA, Borisevich VD. Cascades for separation of multicomponent isotope mixtures [J]. Separation science and technology, 2001, 36(8/9): 1 769-1 817.
[15]Borisevich VD, Sulaberidze GA, Wood HG. The theory of isotope separation in cascades: problems and solutions [J]. Ars Separatoria Acta, 2003(2): 107-124.
[16]Von Halle E. Tennesseeor. Multicomponent isotope separation in matched abundance ratio cascades with losses from each stage [C]// Proc. 1st Workshop on Separation Phenomena in Liquids and Gases, Germany: Darmstadt, 1987:325-356.
[17]Song TM, Zeng S. On the optimity of separation cascade for a binary and multi-component case [C]// Proceedings of the Workshop on Separation Phenomena in Liquids and Gases, China: Beijing, 2006: 132-142.
[18]宋天明,曾實. 多組分氣體離心分離級聯的解析優化 [J]. 清華大學學報(自然科學版), 2006, 46(12): 2 003-2 006.
Tianming Song, Zeng Shi. Optimization of centrifuge cascades for the separation of multicomoponent gas mixtures[J]. Journal of Tsinghua University (Sci & Tech), 2006, 46(12): 2 003-2 006.
[19]Sinev NM. Economics of Nuclear Power Engineering [M]. Moscow: Energoatomizdat, 1987. (in Russian).
[20]Zaritskaya TS, Zaritskii SM, Kruglov AK, et al. Dependence of232U formation in nuclear fuel on neutron spectrum [J]. Atomic Energy, 1980, 48(2): 67-70 (in Russian).
[21]Buttler GG, Wilcox P. Enrichment of recycled uranium [J]. Nuclear Engineering, 1986, 28(6): 186-190.
[22]Atveev LV, Tsentner EM. Problem of232U and236U accumulation in nuclear fuel [J]. Atomic Energy, 1980, 48(4): 10-17 (in Russian).
[23]Matveev LV, Rogozhin VYu.236U compensation in VVER fuel [J]. Atomic Energy 1989, 66(5): 345-349 (in Russian).

