關于Halley法Julia集的對稱性

劉 剛，陳少林，李瀏蘭

（衡陽師范學院 數學與計算科學系，湖南 衡陽 421002）

0 引言及主要結果

給定多項式f（z），則如下定義的公式

稱為關于多項式f的Halley法。該法是一種重要的迭代找根算法，其被關注的程度僅次牛頓法。計算數學工作者對該法進行了大量的研究并取得非常豐富的成果，而從復動力系統的角度進行的研究以及取得的成果相對較少。K.Kneis［1］研究了Hf不動點的性質并給出了一些特殊多項式的Halley法的Julia集的分形圖集。文獻［2］對Hf的Julia集的拓撲結構進行了研究。

Julia集是復動力系統的基本研究對象，我們關心Julia集的拓撲，分形，幾何等性質，鑒于多項式在迭代找根算法下一般都為有理函數，本文只在有理函數范圍內進行研究。有理函數Julia集的對稱性所研究的是有理函數的Julia集的自相似性，涉及的是Julia集的幾何性質。A.F.Beardon［3］研究了臨界有限的有理函數的Julia集的對稱性。隨后G.Levin［4］研究了臨界有限的有理函數的Julia集的對稱性。D.Boyd［5］分析了有理函數的Julia集具有平移不變性的情形。文獻［6］對三類迭代找根算法Julia集對稱性進行了研究。

給定有理函數R（z），則R的Julia集的對稱群∑（R）為保持J（R）不變的共形歐氏變換σ構成的群，即∑（R）＝｛σ：σ（z）＝e2πθiz＋b（θ∈［0，1］）且σ（J（R））＝J（R）｝。給定非線性多項式f（z）＝anzn＋an－1zn－1＋…＋a1z＋a0（an≠0），我們稱為f（z）的形心。如果an＝1且an－1＝0，則這樣的多項式稱為標準多項式。若f（z）為非標準的多項式，令，則T?f?T－1為標準多項式。結合關于多項式的Halley法的動力學性質和關于有理函數Julia集對稱群的知識，我們獲得了如下結果：

定理1 設f（z）為度大于1的標準多項式，則∑（f）?∑（Hf）。

定理2 設f（z）為度大于1的多項式，則平移變換σ＝z＋1∈∑（Hf）當且僅當J（Hf）為一水平直線。

定理3 設f（z）為度大于1的多項式，則J（Hf）為一條直線當且僅當f（z）＝c（z＝－z1）n（z－z2）n（c∈?＼｛0｝，z1≠z2）。此時J（Hf）為連接z1與z2線段垂直平分線。

推論1 設f（z）為度大于1的多項式，則σ＝z＋1∈∑（Hf）當且僅當f（z）＝c（z－z1）n（z－z2）n（c∈?＼｛0｝，z1≠z2，Re（z1）＝Re（z2））。

1 相關定義及引理

設R為復球面?－上的有理函數，，其中P和Q為互素的多項式，degR＝max（degP，degQ）稱為R的度。記Rn為R的第n次迭代。若存在m，k＞0使得Rk（Rm（z0））＝Rm（z0），則稱z0為R的預周期點。特別地，當m＝0時，z0稱為周期點，相應地最小的的k稱為周期點z0的周期。若｜（Rk）′（z0）｜＜1，｜（Rk）′（z0）｜＝1或者｜（Rk）′（z0）｜＞1，則z0稱為（超）吸性，中性或者斥性周期點。R的Julia集J（R）是定義為其斥性周期點的閉包。J（R）補集，即?－＼J（R），稱為R的Fatou集F（R）。J（R）是完全不變的，即R（J（R））＝J（R）＝R－1（J（R）。另外，J（R）沒有完全不變的真閉子集。關于有理函數動力系統更多的定義和結果參見文獻［7，8］。

為證明文中結果，我們還需以下引理。

引理1［3］設f（z）為度大于1的多項式，則對稱群∑（f）是由以f（z）的形心為中心的旋轉變換構成的。如果f（z）是標準的，而且∑（f）是有限的，則∑（f）的階為使得f（z）可表示成f（z）＝zrQ（zm）的最大整數m，其中Q（z）為一多項式。如果對稱群∑（f）是無限的，那么J（f）是一個圓周，并且f（z）共軛于zn，其中n＝deg（f）。

引理2［5］設R（z）為度大于1的有理函數，且J（R）＋1＝J（R）。如果無窮遠點∞是預周期的，那么J（R）是一水平直線或全平面?－。

引理3［1］設f（z）為度大于1的多項式，則多項式f的每一個根都是Hf的（超）吸性不動點。

引理4［2］設f為多項式，g（z）＝az＋b（a≠0）為仿射變換，則g?Hcfog?g－1＝Hf，（c∈?＼｛0｝）。

2 定理的證明

定理1的證明 如果∑（f）是有限的，由引理1知，對任意的σ∈∑（f），存在正整數k使得m為使得f表示成f（z）＝zrQ（zm）的最大整數。從而

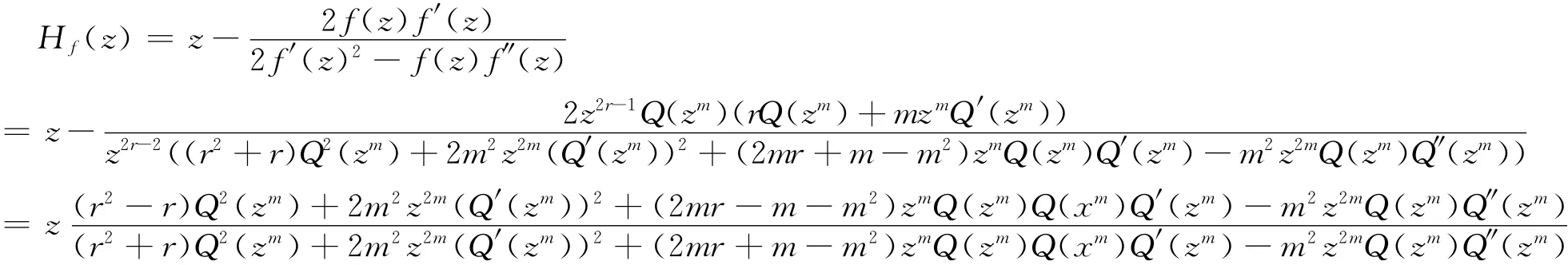
易見σ?Hf?σ－1（z）＝Hf（z），則σJ（Hf）＝J（Hf），從而有σ∈∑（Hf），即證

如果∑（Hf）是無限的，由引理1有f（z）＝zn，其中n＝deg（f）。從而，即知J（Hf）＝∞，顯然有∑（Hf）＝｛σ∶σ（z）＝e2πθiz＋b（θ∈［0，1］）｝。注意到J（f）為單位圓周，從而∑（Hf）＝｛σ∶σ（z）＝e2πθiz（θ∈［0，1］）｝?∑（Hf）。

定理2的證明 當J（Hf）是一水平直線時，顯然平移變換σ＝z＋1∈∑（Hf）。

如果平移變換σ＝z＋1∈∑（Hf），則Hf（z）滿足引理2的條件，故J（Hf）是一水平直線或全平面，然而多項式f（z）至少有一個零點，由引理3，Hf至少有一個吸性不動點，故J（Hf）≠?－，即知J（Hf）為一水平直線。

以下證明當n1≠n2時，J（Hf＊）不能為一直線。注意到

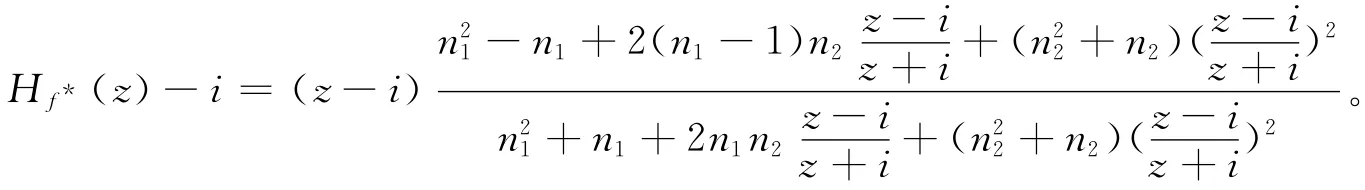
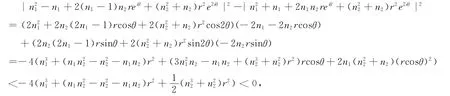
因此｜Hf＊（z）－i｜＜｜z－i｜。因為i為Hf＊的（超）吸性不動點，故｛z∶Im（z）≥3｝包含在i的所在的Fatou分支內。再注意到任意的水平線｛z∶Im（z）＝t｝∪｛∞｝在Hf＊下不是前向不變的，此時J（Hf＊）不可能為一條直線。

接下來證明當n1＝n2?n時，J（Hf＊）為帶無窮點的實軸。此時

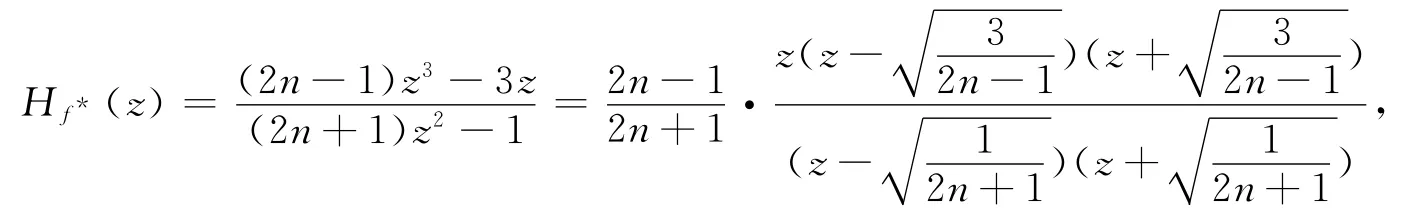
易見Hf＊（?∪｛∞｝）＝?∪｛∞｝。

下證Hf－1＊（?∪｛∞｝）＝?∪｛∞｝。因Hf＊（∞）＝∞且，故∞為Hf＊的斥性不動點，從而∞∈J（Hf＊），又由所以∈J（Hf＊）。對于任意的x，因

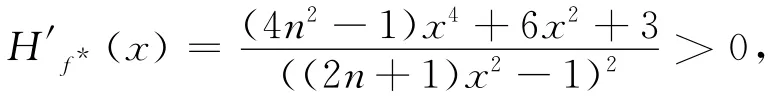
故Hf＊（x）在三個區間以及都是從－∞單調遞增到0；而Hf＊（x）在三個區間以及從0單調遞增到＋∞。從而對任意的x∈?，H－1f＊（x）∈?，可知J（Hf＊）＝?∪｛∞｝.由仿射變換的性質，可知J（Hf）＝g（J（Hf＊））為連接z1與z2線段的垂直平分線。

推論1的證明 結合定理2和定理3的結論即證。

［1］Kneisl K.Julia sets for the super Newton method，Cauchy's method，and Halley's method［J］.Chaos，2001，11：359－370.

［2］Wang X Y，Yu X J.Julia sets for the standard Newton's method，Halley's method，and Schr?der's method for multiple root［J］.Appl.Math.Comput.，2007，189（2）：335－338.

［3］Beardo A F.Symmetries of Julia sets［J］.Bull.London Math.Soc.，1990，22：575－582.

［4］Levin.G.Symmetries on a Julia set［J］.Adv.in Sov.Math.，1991，3：131－141.

［5］Boyd D.Translation invariant Julia sets［J］.Proc.Amer.Math.Soc.，2000，128：803－812.

［6］Yang W F.Symmetries of the Julia sets of Newton's method for multiple root［J］.Appl.Math.Comput.，2010，217（6）：2490－2494.

［7］Beardon A F.Iteration of Rational Functions［M］.Berlin：Springer，1991.

［8］喬建永.重整化變換的復動力學［M］.北京：科學出版社，2010.