基于希爾伯特-黃變換的雙饋異步風力發電機定子故障診斷研究
陳繼寧,馬宏忠,時維俊,陳濤濤
(河海大學能源與電氣學院,南京 210098)
風能作為一種可再生能源,正在受到越來越多的關注。風力發電機中雙饋異步發電機(DFIM)占有很大的市場份額[1]。因此,為了確保電機的安全運行,進行及時的維護和提高運行的可靠性,以及最大化利用風能,電機的在線監測和早期故障診斷具有重要的意義。
與所有的電機一樣,雙饋風機易于發生電氣機械故障,故障可能發生于定子、轉子、軸承、氣隙(偏心)等處。然而,資料表明,電機失效大多數是由軸承故障和定子絕緣擊穿所引起的[2,3]。異步電機定子繞組絕緣劣化是引起電機失效的主要原因(約占40%)[4]。定子故障起始于匝間絕緣的劣化,進而發生匝間短路。因此,需要在匝間短路初期及時地檢測出來,以免故障擴大造成崩潰或重大損傷。
當雙饋風力發電機發生定子繞組匝間短路時,如果故障比較輕微,三相定子電流的變化非常微小,此時僅從時域波形無法識別出是否存在定子匝間短路故障[5]。傳統的傅里葉變換是整個時間軸上的積分,因此不能給出時間域的信息,只適用于穩態信號的特征提取,對于變化中,或者剛發生故障的信號并不能有準確的判斷[6]。小波變換(WT) 是 20 世紀 80 年代由法國地球物理學家J Morlet在分析地震波時提出的一種非平穩信號分析理論,近年來在信號分析方法上有重大突破,并已在故障診斷領域得到成功應用[7,8,9]。在分析頻率逐漸變化的數據時,小波變換很有效,其結果具有解析形式。但小波變換主要基于傅里葉分析,不可避免具有傅里葉分析的局限性。對于正常頻率與故障頻率基本相同或變化微弱的信號,如早期匝間故障造成的信號的微小變化,小波變換則無法有效提取其故障特征[10]。
本文采用希爾伯特-黃變換(Hilbert-Huang Transform)[11]對雙饋風力發電機定子繞組故障進行分析,即對在動模實驗室采集到的電流信號進行變換,根據第4或者第5層固有模態函數(IMF)分量的瞬時幅值或瞬時頻率可以確定出匝間短路故障及其出現和結束的時刻,便于定子匝間短路故障的實時監測、確定和及時維修。
1 希爾伯特-黃變換方法
希爾伯特-黃變換(HHT)是美國宇航局(NASA) 的Norden E Huang等人于1998提出的一種新的時間序列信號分析方法,這是在歷史上首次對Fourier變換的基本信號和頻率定義作的創造性改進,主要應用于非平穩信號,尤其是突變信號的分析。
HHT方法由 EMD和 Hilbert變換兩部分組成,EMD分解用來提取經驗模態函數(IMF);然后對 IMF進行Hilbert變換可獲得瞬時頻率和瞬時振幅,二者皆為時間的函數。根據瞬時頻率或瞬時幅值可進行故障特征提取。下面將HHT應用于電機故障診斷。
1.1 EMD方法對 i(t)進行分解
電機電流信號均包含有多種振蕩模態,直接對其進行Hilbert變換得到的瞬時幅值是毫無意義的。EMD基于信號的局部特征時間尺度,可以將任意復雜的信號分解為少量 IMF的組合, IMF表征了內蘊于數據的振蕩模態[12]給出合理的瞬時幅值,IMF分量必須滿足下面兩個條件:一是在整個數據長度上,信號極值點的數量與過零點的數量相同或者至多相差 1個;二是在任意點,由局部極大值點構成的包絡線和局部極小值點構成的包絡線的平均值為零。這樣一個信號可以表示為若干個IMF和一個殘差的和,如下式所示
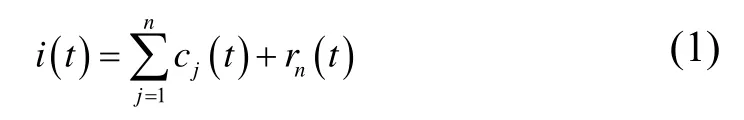
其中mj(t)是第j個模態函數,rn(t)是殘差。
為了提取信號i(t)的模態函數,步驟如下:
(1)將原始信號i(t)上所有的極大值點用三次樣條函數擬合成數據的上包絡線,所有的極小值點擬合成下包絡線,上下包絡線的均值,記為m1(t);
(2)將原始信號i(t)減去該均值即可得到一個去掉低頻的新數據序列h1(t);
(3)h1(t)一般仍不是一個 IMF分量序列,為此需要對它重復進行上述處理過程,直到h1(t)符合 IMF的定義要求,這樣就得到了第1個IMF分量c1(t),它代表信號i(t)中最高頻率的分量;
(4)將c1(t)從i(t)中分離出來,即得到一個去掉高頻分量的差值信號r1(t),即有

將r1(t) 作為原始數據,重復步驟(1)、(2)和(3),得到第二個IMF分量c2(t),本文重復6次 ,得到6個IMF分量。
1.2 IMF的希爾伯特變換
電流信號i(t)的Hilbert變換H(t)為
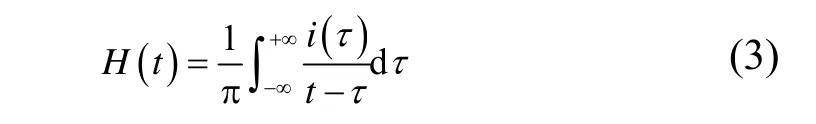
其反變換為
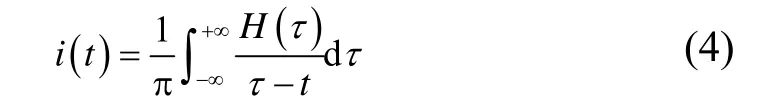
則與之形成復共軛時,由其構成的解析信號為

式中:a(t)為瞬時振幅,θ(t)為相位。
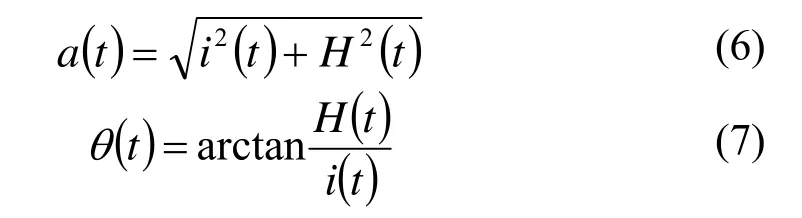
2 實驗測試與研究
采用了如圖1的系統結構圖來測試不同負載下的雙饋風機定子電流。直流電動機與雙饋異步發電機(用YZR160M-4繞線異步電機代)之間用機械連接,直流電動機的轉速模擬風速,帶動繞線式異步電機轉動。定子側通過升壓變壓器與電網相連;轉子側有勵磁系統,轉子繞組通過變頻器實現對風力發電系統的變速恒頻控制。
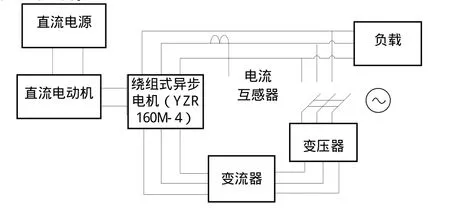
圖1 雙饋風機定子繞組匝間短路故障實驗原理圖
YZR160M-4電機主要參數如下:定子額定電壓:380V,定子額定電流:12.5A,轉子額定電壓:184V,轉子額定電流:20A,電機額定功率:5.5kW,4極。直流電動機型號為Z2-51,額定功率:5.5kW,額定電壓:220V,額定電流:30.9A,額定轉速:1500r/min。電流互感器型號為ML-6.0。數據采集裝置選用尼高采集儀,型號為Nicolet7700。
發電機的定子繞組在設計階段就已經安裝好抽頭,通過抽頭的連接實現定子繞組內部一匝短接,來模擬匝間短路初期故障。考慮到匝間短路對電機壽命的影響,故抽頭短接時間越短越好,最大不超過1秒。
系統分別在空載、半載以及額定負載情況下,進行了定子繞組一匝短路故障試驗。采集到的三相定子電流實測波形圖如圖2所示,可以看出故障發生時,三相定子電流的變化非常微小,僅從時域波形很難識別出是否存在定子匝間短路。下面以額定負載情況為例進行說明:對發電機定子三相電流進行FFT分析(圖3),可以看出故障情況下與正常狀態差別不大。在對發生瞬態匝間短路的定子電流信號進行小波分析時,同時對小波基 db1 、db2 、db3 、db5 、sym1 、sym2 、sym3 、sym5 、coif1 、coif3 、coif5 都進行了嘗試,沒有發現故障特征。圖4以db2小波為例,可以發現短路發生時,并沒有引起小波分解信號的突變。
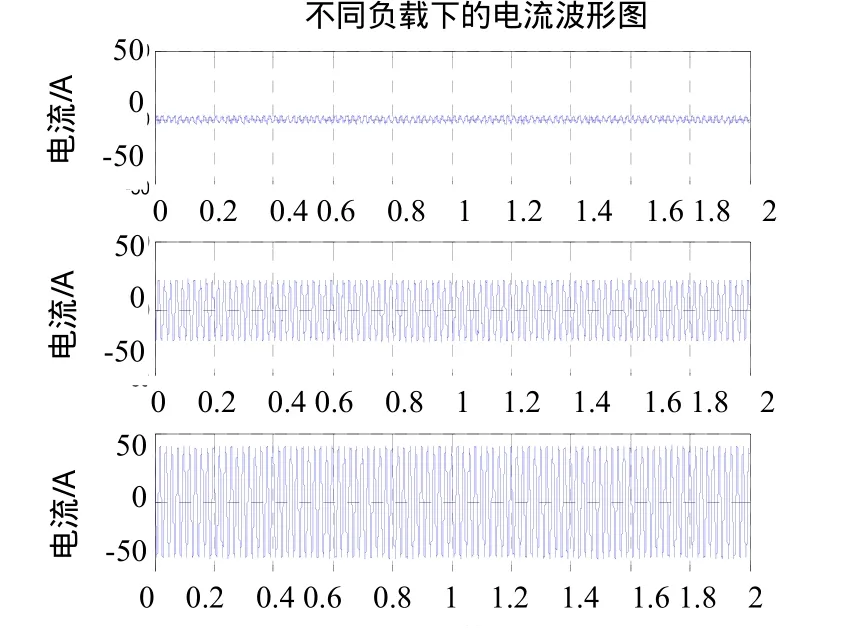
圖2 雙饋風機在空載(上)、半載(中)和額定負載(下)下定子匝間短路時定子電流波形圖
圖 5(a)~5(b)為實驗測得的雙饋電機在空載情況下的電流信號的 6層經驗模態函數 IMF圖及其 Hilbert變換后的瞬時幅值圖,圖 6(a)~6(b)為半載情況下的IMF圖以及其Hilbert變換后的瞬時幅值圖,圖7(a)~7(b)為額定負載情況下的IMF圖以及其Hilbert變換后的瞬時幅值圖。
由圖5、圖6和圖7可以看出,HHT 得到的第4或者第5層IMF分量的瞬時幅值在故障產生和切除的時刻均有很大的突變,可以表征故障,獲取故障產生和切除的時刻。這是因為,HHT根據信號包絡分解出高頻分量,由于三相短路故障中故障造成的幅值變化會引起信號包絡的改變,使信號包絡包含故障信息。如圖5,6和7所示,第4或者第5層IMF的瞬時幅值所具有的故障特征正是這一故障信息的表現。因此,在造成信號包絡變化但頻率基本不變或變化微弱的故障情況下,傳統的傅里葉變換以及小波變換均無法判斷,此時HHT顯示了它的優勢和判斷的及時性和準確性。
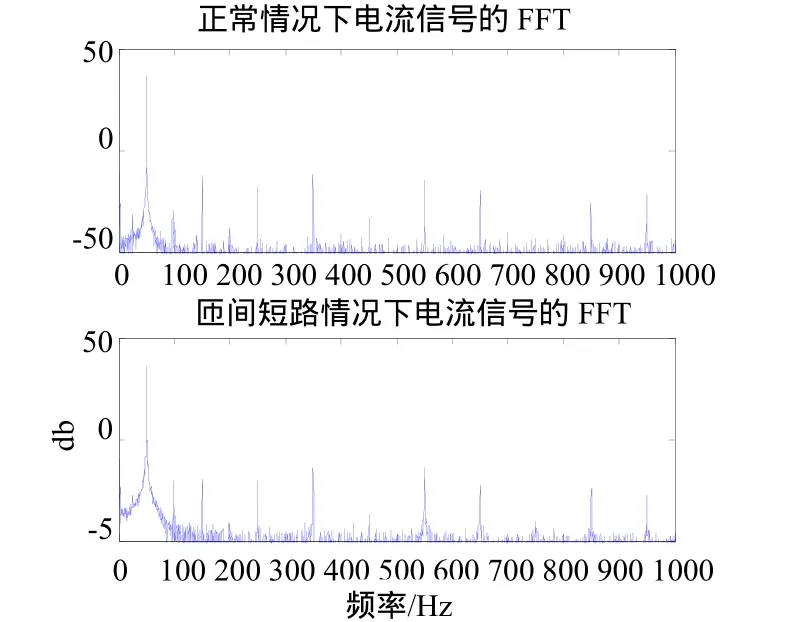
圖3 雙饋風機在額定負載時正常和匝間短路情況下的定子電流信號的頻譜圖

圖4 雙饋風機額定負載情況下定子匝間短路時定子電流信號的小波分解
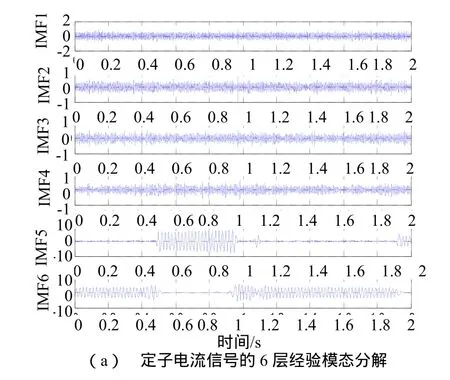

圖5 雙饋風機空載情況下定子匝間短路時定子電流信號的希爾伯特-黃變換
由雙饋風機在空載、半載以及額定負載下定子電流希爾伯特-黃變換的瞬時幅值圖可以看出,在故障初期即匝間短路發生的瞬間,瞬時幅值發生突變,因此可以判斷出故障的發生。但是希爾伯特-黃變換只能判斷出故障的發生,并不能在已經發生故障時估計故障的嚴重程度,也不能對故障位置進行準確定位,需要結合其他方法進行故障監測與診斷。

圖6 雙饋風機半載情況下定子匝間短路時定子電流信號的希爾伯特-黃變換
3 結論
本文通過實測數據對雙饋異步風力發電機定子繞組故障進行研究,通過比較傳統的FFT分析、小波分析以及HHT分析,指出第4或者第5層IMF瞬時幅值分析的優越性。分別對雙饋發電機在空載、半載以及額定負載運行時的定子繞組匝間短路進行實驗分析,得到如下結論:(1)在匝間短路故障比較微弱的時候,三相電流的變化非常微小,此時僅從時域波形無法識別出匝間短路的發生;(2)在匝間故障發生時,信號的頻率幾乎不發生變化,此時僅有信號幅值的變化,小波變換無法有效提取其故障特征;(3)對電流信號進行希爾伯特-黃變換,得出6層IMF的瞬時幅值圖,可以看出,當匝間短路發生時,無論是空載、半載和額定負載,信號的第4或者第5層IMF的瞬時幅值均發生突變,可以判斷匝間短路故障的發生,為匝間短路的及時發現與維修提供了一個有效的手段。

圖7 雙饋風機額定負載情況下定子匝間短路時定子電流信號的希爾伯特-黃變換
[1]Popa L M, Jensen B B, Ritchie E, et al. Condition monitoring of wind generators[C]//Industry Applications Conference, 2003. 38th IAS AnnualMeeting. Conference Record of the. IEEE, 2003, 3:1839-1846.
[2]Vas P. Parameter Estimation, Condition Monitoring,and Diagnosis of Electrical Machines (Monographs in Electrical and Electronic Engineering)[M].London, UK: Oxford Univ. Press, 1993.
[3]Nandi S, Toliyat H A. Condition monitoring and fault diagnosis of electrical machines-a review[C]//Industry Applications Conference, 1999.Thirty-Fourth IAS Annual Meeting. Conference Record of the 1999 IEEE. IEEE, 1999, 1: 197-204.
[4]Thomson W T, Fenger M. Current signature analysis to detect induction motor faults[J]. Industry Applications Magazine, IEEE, 2001, 7(4): 26-34.
[5]魏書榮, 符楊, 馬宏忠. 雙饋風力發電機定子繞組匝間短路診斷與實驗研究[J]. 電力系統保護與控制, 2010, 38(11): 25-28.
[6]Gritli Y, Stefani A, Filippetti F, et al. Stator fault analysis based on wavelet technique for wind turbines equipped with DFIG[C]//Clean Electrical Power, 2009 International Conference on. IEEE,2009: 485-491.
[7]Zhang Z, Ren Z, Huang W. A novel detection method of motor broken rotor bars based on wavelet ridge[J]. Energy Conversion, IEEE Transactions on,2003, 18(3): 417-423.
[8]Douglas H, Pillay P, Ziarani A K. A new algorithm for transient motor current signature analysis using wavelets[J]. Industry Applications, IEEE Transactions on, 2004, 40(5): 1361-1368.
[9]宋志明, 霍永紅等. 基于小波變換的HVDC 輸電系統故障診斷研究[J]. 電力系統保護與控制,2012, 40(3): 100-104.
[10]楊露, 沈懷榮, 希爾伯特-黃變換與小波變換在故障特征提取中的對比研究[J]. 兵工學報, 2009,30(5): 628-632.
[11]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,1998, 454(1971): 903-995.
[12]劉毅華, 趙光宙, 希爾伯特-黃變換在電力系統故障檢測中的應用研究[J]. 繼電器, 2006, 34(14):4-6.

