兩人問題解決中慣例的測量及其微觀發生過程*

張 梅 辛自強 林崇德

(1中央財經大學社會發展學院心理學系,北京 100081)(2北京師范大學發展心理研究所,北京 100875)

1 引言

問題解決作為心理學的核心議題,其研究長期以來限于單個人,較少涉及兩人及以上群體。然而,這不符合大多數問題的解決是靠集體力量完成的生活現實。慣例(routines)作為組織的核心特征(此時一般稱為組織慣例),是March和Simon(1958)提出的用群體問題解決思路探討組織問題構想的例證,其研究涉及社會科學領域各個分支(Feldman &Pentland,2003;Salvato &Rerup,2011)。本研究綜合以往論述(Becker,2008;Cohen &Bacdayan,1994;Egidi,1996),從操作定義的角度將慣例界定為兩人或多人在面臨重復性的問題解決任務時習得的、互相依賴的、可識別的、行為模式或策略。這一概念從認知和行為兩個角度界定了慣例,為實驗研究的開展奠定了基礎。

從個體層面理解的慣例始于 20世紀 40年代Luchins(1942)有關思維定勢的一系列研究。群體層面慣例的實驗研究始于Cohen與Bacdayan(1994)發明的撲克牌游戲(Target The Two,簡稱TTT),它被評為慣例整體上缺乏實驗研究大背景下“最重要的例外”(Becker,2008,p.301)。本游戲使用6張撲克牌(2?,3?,4?和 2?,3?,4?)由兩人合作完成,格局見圖1：每個玩家各持一張牌(看不到對方的牌,不允許交流),其余4張牌分兩明兩暗4張牌擺在桌面上。游戲目標是通過兩人輪流用手里牌與桌面上的牌進行交換(可不換,但仍算走了一步),將 2?換到目標位置。首先換牌的一方為同色玩家(她),只有當她手中的牌與目標位置的牌是同花色時(均是?或?),才能換目標位置的牌。另一方為同點玩家(他),只有當他手中的牌與目標位置的牌是相同點數時(均是2,3或4),才能換目標位置的牌。換其他位置的3張牌無任何限制。換牌后,保持牌原先明暗不變。每完成一局小組將獲得一定獎勵(如 1美元),但每走一步要扣掉一定獎勵(如 1美分),游戲結束后兩玩家將獲益平分。游戲一般約進行40局。1996年Egidi將現場進行的游戲改為計算機版。

Cohen和Bacdayan(1994)認為本實驗模擬了組織生活的一些基本特征：同色和同點玩家的限定造成能力的不對稱以及對能力和角色分配的可能性;玩家手中的牌及桌面暗牌造成了信息的不對稱和不確定;總體來說,通過合作兩個玩家都能獲益,但當合作失敗時兩人的效率還不如一個人的效率高;各小組成員的角色會隨著各小組發展出有效的游戲方法而逐漸構建起來;這種學習過程形成了一個微小而短暫的組織。

圖1 TTT游戲的初始牌局

游戲中慣例的測量通過四個判定指標實現(Cohen &Bacdayan,1994)：(1)可靠性增加。這一指標體現了組織處理問題能力的提高,可用所有玩家玩每局游戲時所需步數的變異性體現。(2)速度增加。面對陌生環境時慣例化的行為要比深思熟慮的決策快。它可用玩家完成游戲所用時間隨局數增加而減少來體現。(3)重復的行動序列。構成慣例的諸多行為是隨時間重復的,玩家會逐漸從“一次考慮一步”發展為一次考慮一個“組塊”。(4)偶爾的次優性。游戲中玩家會被鎖定于某行動序列,即使有更有效的方法也不去采用。此外,Egidi(1996)通過關注目標位置牌的移動構建了本游戲的問題空間圖(圖2),提出了驗證慣例的第5個指標——基于特定策略的反應模式。

圖2 TTT撲克牌游戲的問題空間圖

作為一個界定良好的問題,TTT撲克牌游戲獲得了很多贊譽,但它并未像問題解決研究中的漢諾塔任務那樣得到廣泛應用,個案近年來仍是慣例研究的主流(De Boer &Zandberg,2012;Labatut,Aggeri,&Girard,2012)。這一是由于TTT撲克牌游戲任務規則及完成過程復雜,使其超過兩人便難以進行實驗操縱和結果解釋。例如,王建安和張鋼(2008,2010)開發的三人版任務中,問題空間圖呈網狀復雜結構。二是,驗證和描述慣例的各項指標均可繼續細化和改進：(1)可靠性。這本質上代表問題解決效率的提高。原先四分位差指標雖具合理性,卻非原始數據,用玩家每局所用步數及每局的獲益的變異可能會更直觀地體現問題解決效率的提高。(2)速度。這本質上是從時間角度體現問題解決效率提高。除用被試組完成每局游戲所用平均時間外,還可用每組被試完成每局游戲所用總時間及每一局游戲的平均步時來刻畫。(3)重復的行動序列。可嘗試用量化方法描述重復的行動模式,并探索被試每步換牌選擇的位置上的行為固著。(4)偶爾的次優性。可嘗試通過個案分析更為直觀地展示。

與實驗研究進展緩慢形成對比,慣例在組織行為學、管理學和經濟學領域的研究取得了豐碩成果并出版了《組織慣例手冊》(Becker,2008),但其研究中仍存在如下懸而未決的問題：(1)慣例的意識性。慣例是自動、無意識的(Cohen,1991;Stene,1940),還是需要意識努力(Feldman,2000;Feldman&Pentland,2003)的？當前存在兩派截然不同的觀點。(2)慣例的穩定性。基于生成觀理論(Feldman &Pentland,2003;Pentland &Feldman,2005;Pentland,Feldman,Becker,&Liu,2012),慣例同時具有穩定性和變化性,這可解釋組織技術及知識創新、演化、動態能力的形成、組織適應等。然而,這些大多基于理論推斷,缺少實驗研究的支持。(3)慣例與陳述性知識的關系。自Cohen和Bacdayan(1994)證實慣例作為程序性記憶存儲后,研究者們大多在這個框架下討論慣例的特點,很少關心慣例形成和變化過程中陳述性知識的作用。王建安和張鋼(2008)證實帶有陳述性知識特征的圖式對慣例具有重要影響,但未說明慣例本身是否含有陳述性知識的成分。

上述問題集中體現為當前缺乏慣例從無到有產生過程的研究。受研究方法的局限,當前大多研究只能對已存在的慣例進行分析,無法分析其形成過程。心理學中用于探測認知變化的微觀發法使之成為可能。微觀發生法作為一種特殊的發生法和縱向研究方法,可以細致地刻畫學習過程如何發生,現已廣泛應用于探測問題解決中幾天、幾周內的認知和策略變化(辛自強,林崇德,2002;Kuhn,Goh,Iordanou,&Shaenfield,2008;Luwel,Siegler,&Verschaffel,2008)。慣例作為問題解決中形成的策略,存在從無到有的產生過程;同時,計算機可以記錄TTT撲克牌游戲中的所有變化。因此,理論上微觀發生法的分析思路可以探測慣例產生過程。然而,微觀發生法本質上只是一種精細的實驗設計和數據分析的思路,它相當于一個放大鏡,將認知變化的路線、速率等清晰地呈現于人們的視野中。但是,放大鏡具體應聚焦于多局游戲(相當于重復進行了多次問題解決)的哪個位置,還需要相應理論的指導。Kamiloff-Smith(2001)提出的表征重述理論可能滿足了這種需要。本理論認為,知識或策略的獲得是個體對原有表征不斷進行重組、建構,逐漸把行為程序中存儲的內隱知識轉變為外顯知識,并為認知系統其它部分所利用的過程。受這一理論啟發,可將多局 TTT撲克牌游戲劃分為不同階段,分析每個階段內行為的變化。

綜上,本研究的目的一是對基于 TTT撲克牌游戲的兩人問題解決中的慣例進行驗證和描述,將Cohen和 Bacdayan(1994)提出的指標進一步完善;二是采用微觀發生法的設計和分析思路,對慣例從無到有的產生過程進行描述,解決以往研究中有關其意識性、穩定性及與程序性知識關系的爭議。

2 研究方法

2.1 被試

選取某大學本科生70名,由計算機隨機分為35組。其中,男—男、男—女和女—女組的人數分別為8、14、13。經確認,所有被試均未參加過類似測試。

2.2 實驗平臺及實驗設計

本測驗由專業的程序員采用 ASP.NET和 C#語言在windows server 2008環境下進行程序開發,使用 IIS7作為網絡服務器開發相應的測驗及操控平臺。測試時,被試注冊并學習完游戲規則后,隨機進入某個 2人房間完成測試(界面如圖3)。電腦自動記錄每個玩家每步換的牌、所用時間以及每局各組得分、步數和時間。

按照微觀發生法的設計要求,測驗任務需多次重復。本研究基于 TTT撲克牌游戲的問題空間圖(圖2),將初始位置的撲克牌固定為 4?(保證完成每局游戲的最優策略相同)設計了40局游戲。為控制 2?所在位置對初始牌局難易程度產生的影響,對 2?出現的 5個位置(除目標位置外)進行了平衡,即每個位置均出現 8次。此外,借鑒 Egidi(1996)的設計思路,40局中設置5局重復的游戲模板,將前5局出現的模板在后5局重復出現。被試組每完成一局游戲獲得100分,每走一步扣2分。測驗完成后,按照每組獲益給予被試 5～15元不等的獎勵,并讓其填寫包含個人信息和實驗信息的問卷,同時反饋自己是否意識到所采用的策略及與組員配合的過程。

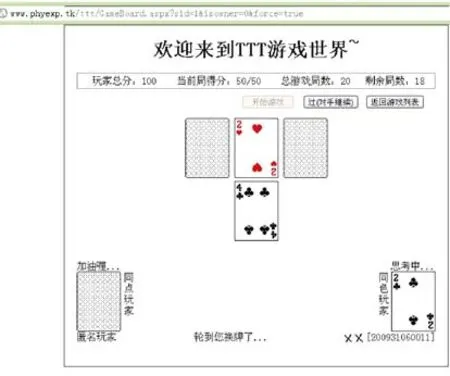
圖3 TTT撲克牌游戲界面

數據以 Excel格式從數據庫中導出后,將每條記錄以小組為單位進行整理：計算每組被試每局所用的步數、時間、得分、所用策略(據目標位置牌的移動整理)及行動序列。其中,被試換牌的行動序列與前人一致,用如下符號刻畫(Bonini &Egidi,1999;Cohen &Bacdayan,1994;Egidi,1996)：U—換明牌;C—換同色玩家左側的暗牌;N—換同點玩家右側的暗牌;T—換目標位置的牌;P—過牌不換。

3 結果與分析

3.1 各組被試表現的描述

首先,整體來看,35組被試在40局游戲中平均每局游戲獲得 86.84分,7步完成,用時 2292.50s,每步用時8.77s。由策略選擇的事后分析可知,35組被 試 大 多 應 用 4?2?2?(平 均 22.00 次)和4?4?2?(平均15.49次)兩種最優策略,其他目標位置牌需經 3次(如 4?3?3?2?、4?3?2?2?)、4次及以上(4?2?3?3?2?、4?4?3?3?2?2?)變換的次優策略平均應用2.6次。通過對每個游戲模板上被試表現的描述發現,40個游戲模板中,被試組在模板9上表現最好,在模板2上表現最差。

為測查是否經過多局反復解決類似問題,各被試組解決問題的效率得到了提高,研究采用事前事后設計的思路對前后5局游戲各項指標進行了對比,結果見圖4。

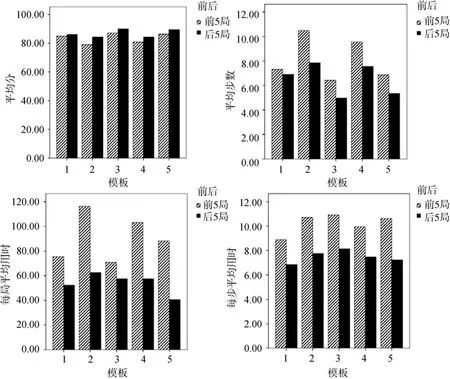
圖4 前后5模板每局得分、所用步數、每局用時、每步用時的差異

在得分上,前 5局總分顯著低于后 5局(

t

=?3.05,

p

＜0.01),但只有模板2及3上前后5局的差異達到了顯著性水平(

t

=?2.13,

t=

?2.27,

ps

＜0.05);在所用步數上,前后5局總分差異不顯著(

t

=?0.88,

p

＞ 0.05),但模板 2、3、4 上前后 5 局的差異顯著,

ps

＜0.05;在每局所用時間上,前5局顯著高于后5局(

t

=3.96,

p

＜0.001),但只在模板 2(

t

=3.11,

p

＜0.01)和4(

t

=2.71,

p

＜0.05)上達到了顯著性水平;在每步的平均用時上,前5局顯著高于后5局(

t=

4.23,

p

＜0.001),且每個模板上的差異均達到了顯著性水平。表1為每個模板上前后 5局所用策略的變化數。后5局與前5局相比,4?2?2?策略的使用增加了18次,4?4?2?策略的使用減少了7次,其他策略的使用減少了 11次。對上述差異的卡方檢驗表明,只有其他策略的使用次數達到了顯著性水平,χ=4.48,

p

＜0.05;4?2?2?和 4?4?2?策略的使用次數前后5局差異均不顯著,χ=0.41/ 0.01,

ps

＞ 0.05。

3.2 TTT撲克牌游戲中的慣例

由上述結果可知,重新設計后的40局TTT撲克牌游戲中可能存在慣例,下面繼續按照前述的 5個指標對慣例進行系統驗證和描述：

表1 各模板前后5局采用策略的變化數

(1)可靠性增加。分別以玩家完成每局游戲所用的步數和每局獲益為因變量,以局數為自變量進行回歸分析,結果表明,隨著局數的增加,被試組完成每局游戲所用步數逐漸減少,

β

=?0.10,

t

=?3.87,

p

＜0.001;每局的獲益逐漸提高,

β

=0.10,

t

=3.83,

p

＜0.001。(2)速度提高。分別以被試組完成每局游戲所需的時間和平均步時(每一局游戲的所用時間除以所用步數)為因變量,以局數為自變量,進行回歸分析,結果表明,隨著局數的增加,被試組完成每一局游戲所用時間和完成每一步的平均時間均在減少,

β

=?0.16,

t

=?6.05,

p

＜0.001;

β

=?0.11,

t

=?4.07,

p

＜0.001。(3)重復行動序列。對每組被試完成每局游戲的行動序列進行總結發現,在1400(40×35)局游戲中,以第1步換牌位置為起點,存在如表2所示的典型模糊行動序列。例如,“CC*T*T”代表第1步時同色玩家選擇換右上位置的牌,之后同點玩家也選擇換右上位置牌,中間經過數次變換,兩位玩家均換了目標位置的牌而達成目標。由表可知,不論玩家第1步選擇換哪個位置上的牌,都存在一定的行為模式。對上述5類模糊行動序列次數的卡方檢驗表明其差異達到了顯著性水平：χ=262.11,

p

＜0.001。

除上述模糊的行動序列之外,在所有 1400(35×40)局游戲中,被試組完成每局游戲的完整行為模式也存在重復,表3為應用次數超過20次的行為模式。例如,“換目標位置牌→換明牌→過牌→換目標位置牌”(即 TUPT)的行動序列作為獨立策略完成了54局游戲,還作為“組塊”在153局游戲中出現。

(4)基于特定策略的反應模式。由上述分析可知,各被試組對4?2?2?和4?4?2?兩種最優策略具有不同程度的依賴性。

(5)偶爾的次優性。對每個游戲模板上采用策略的分析發現,被試一旦認定了某策略,即使有更好的策略也不會采用。以模板 19(圖5)為例,若被試組選擇 4?4?2?策略,5步即可快速完成(PUPTT)游戲;若選擇4?2?2?策略(共15組),則需先尋找暗牌 2?,這可能會造成多次反復并應用次優策略(2組),進行8步以上甚至多達到14步之多的換牌。

由上述分析可知,在 TTT撲克牌游戲為任務的兩人問題解決中存在明顯的慣例現象,其主要體現為對兩種最優策略和不同行動序列的堅持。在此基礎上,研究繼續采用微觀發生法的分析思路探討慣例的產生過程,尤其是策略的形成和變化。

表2 重復的行動序列模式

表3 每局游戲行為模式的應用次數

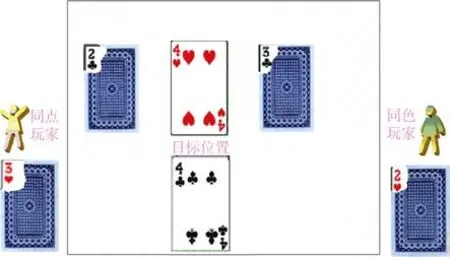
圖5 模板19的初始牌局

3.3 TTT撲克牌任務的階段劃分

依據前述的表征重述理論(Kamiloff-Smith,2001)將40局游戲劃分為4個階段,每階段各被試組表現見表4。由表可知,四階段各項指標的變化模式是統一的：得分上四個階段依次升高;每局所需步數、每局所用時間、每步所用時間上四階段依次降低。

表4 不同階段35組被試的表現

為了檢測上述各差異是否達到顯著性水平,分別以四項指標為因變量,以階段為自變量進行單因

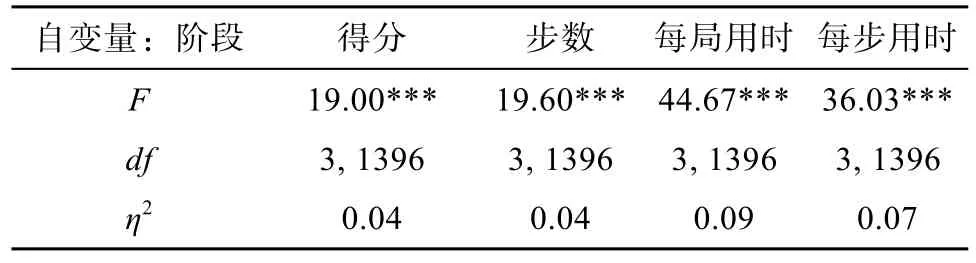
表5 不同階段35組被試的表現的方差分析

素重復測量的方差分析(其結果與單因素隨機區組設計完全一致)。由表5可知,階段主效應在四個因變量上均達到了顯著性水平(

ps

＜0.001)。進一步事后檢驗(LSD)結果表明,階段Ⅰ的各項指標與其余3個階段差異顯著,但3個階段之間均無顯著差異。

由上可知,被試的各項行為指標在不同階段均發生了變化,下面繼續采用微觀發生法的分析思路從變化的路線、變化的速率、變化模式的多樣性、變化的來源四個方面探討慣例產生過程的特點。

3.4 變化的路線

3.4.1 四個階段策略使用率的變化

圖6為四個階段不同策略的使用頻率,其計算方式為本階段內某策略的使用次數除以 350(35×10=350)。由圖,雖然兩最佳策略的使用率分別由階段Ⅰ的56%、33%上升到階段Ⅳ的59%、39%,但對次數的卡方檢驗表明,上述差異并不顯著,χ=2.20,χ=6.90,

ps

＞ 0.05。其他策略的使用率由階段Ⅰ的11%持續下降為階段Ⅳ的2%,且對次數的卡方檢驗表明,上述差異在四階段內達到了顯著性水平 χ=30.80,

p

＜0.001。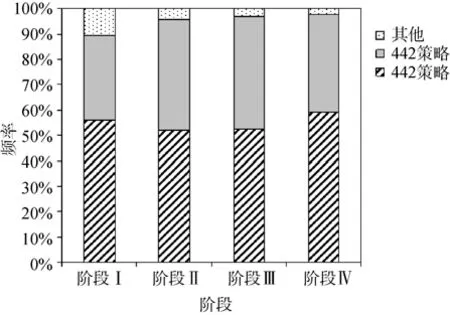

圖6 不同階段策略使用頻率的變化

3.4.2 四個階段行為模式的變化

圖7為四個不同階段第1步同色玩家換5個位置牌的次數變化。第1步選擇換右上位置的牌的各種行為模式(C)的次數從階段Ⅰ的 35%下降到階段Ⅳ時的 30%,卡方檢驗表明,其差異達到了顯著性水平,χ=55.39,

p

＜0.001。其余行為模式的使用次數雖然在四個階段不斷變化,但差異均未達到顯著性水平。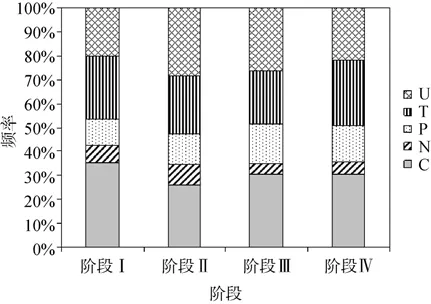

圖7 不同階段行為模式使用頻率的變化

3.4.3 策略變化的順序——聚焦于階段Ⅰ

與策略和變化路線密切相關的問題是：被試組的行為模式及其使用策略是按照怎樣的先后順序出現的？又經歷了怎樣的變遷？這其中最主要的問題是兩人如何配合確認問題解決的最優策略并堅持下去。由表4可知,各被試組行為指標的變化主要集中于階段Ⅰ。因此,研究通過分析階段 10Ⅰ局游戲中各組被試的策略表現嘗試回答上述問題。經分析,第1局游戲時,有 17組被試采用了4?2?2?策略,12組采用了 4?4?2?策略,6組采用了其他策略。之后,35組被試策略的使用分為如下情況：

①堅持第1局應用的策略不變。10局中堅持多少局才算真正在應用此策略而非偶然或猜測？這可轉化為這樣一個概率問題：在 10次重復的選擇中,被試每次在 3個不同策略選項中選擇某策略的次數為多少時,才證明他不是猜測？利用二項分布原理,可計算出偶然選擇某策略的概率,其公式為：

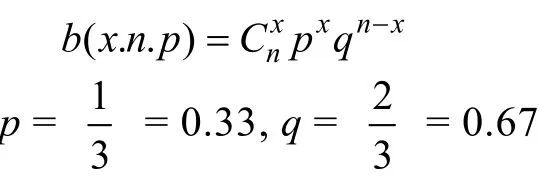
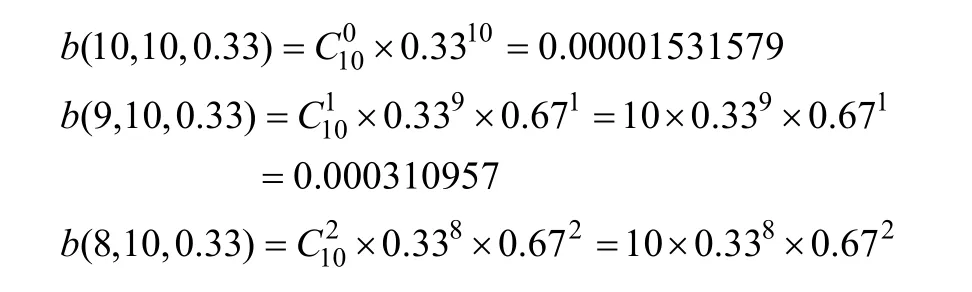
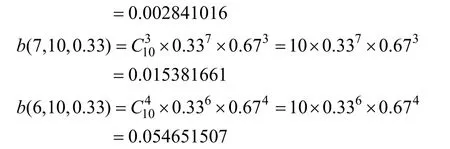
根據以上計算的每局游戲猜對某策略的概率,可用概率加法求得猜對本策略 7題以上的概率為0.018549,不足5%,因此,10局游戲中,有7次及以上選擇某策略才算真的在使用某策略,不是偶然或者猜測,作此結論尚有95%犯錯誤的可能。通過分析,共有 8組被試在階段Ⅰ堅持應用了 4?2?2?策略;2組被試應用了4?4?2?策略。

②將第1局應用的策略調整為其他策略。應用上述方法可以計算出除第1局外的9局游戲中選擇某策略6局及以上不是猜測,而是對策略的堅持。通過分析,共有 6組被試是這種情況,均為由4?4?2?或其他策略變為 4?2?2?策略。

③偏向兩種最佳策略之一。偏向是指將某些其他策略視為兩最佳策略的變式后,10局中有 7次,或9局中有6次采用某最佳策略。例如,4?2?3?2?2?策略可視為 4?2?2?策略的變式,因為二者均由同點玩家用2?與目標位置的2?交換結束任務。經統計,有8組被試明顯偏向 4?2?2?、3組被試明顯偏向 4?4?2?策略。

④兩種最佳策略并存。共有6組被試屬于這種情況。第25組被試兩種策略各使用5次,且無其他策略;第33組被試除前2局采用其他策略,兩策略各使用4次;第13、14、23和26組被試將其中其他策略視為不同變式后,兩策略的使用次數相等。

⑤無固定策略,一直處在摸索中。共有2組被試屬于這種情況。

3.5 策略變化的速率

通過上述分析可知,四個不同階段被試組采用的策略在不斷變化,這種變化的速率如何？這可通過分析相鄰兩個階段內3種策略使用次數的變化及其差異檢驗來回答。由表6可知,只有階段Ⅰ和階段Ⅱ中4?4?2?策略的增加及其他策略的減少達到了顯著差異：χ=4.80,

p

＜0.05;χ=9.31,

p

＜0.01,其他相鄰兩階段三類策略的使用次數均無顯著性差異。這表明策略的變化在階段Ⅰ和階段Ⅱ間最為明顯和迅速,其余階段間相對隱蔽和緩慢。

3.6 策略變化模式的多樣性

由上述策略變化路線的分析可知,TTT撲克牌游戲中策略變化模式存在多樣性。通過每組被試在四個不同階段采用策略的變化,可以全面分析策略變化模式的特點,結果見表7。

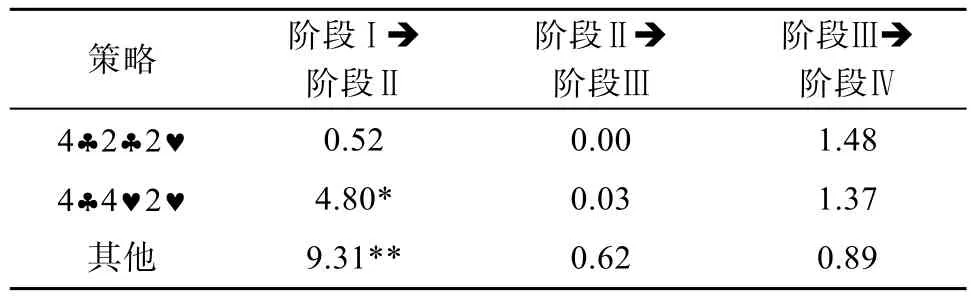
表6 35組被試不同階段策略使用次數的卡方檢驗

通過上述計算猜測率的方法,表7中“固定”的涵義為10局游戲中,7局及以上選擇了某策略;“調整”的涵義為10局中堅持某策略不到7局;“偏向”的涵義為將一些其他策略視為本策略后,10局中有7局使用本策略或者9局中有6局使用本策略;“并存”的涵義為兩種最佳策略各采用 5次或去掉其他策略后,使用兩種策略的次數相等。由表可知,35組被試在四個實驗期間表現出 33種變化模式,可謂復雜多變。

3.7 策略變化的來源

通過事后訪談可知,TTT撲克牌游戲后期幾乎所有被試組均意識到了兩人所采用的策略,這些策略經由雙方互相磨合形成,磨合的過程是策略和行為模式變化的主要原因。

(1)策略形成的方法

第一,心中有明確的策略,主動創造條件配合對方或等待機會。例如,有玩家說：我要拿紅心2,等待對方把梅花 2放在目標位置去換以完成游戲(01-D)。可見,作為同點玩家的他腦中有清晰的4?2?2?策略。再如,還有玩家結合自己身份主動配合對方：因為我是同點玩家,達成目標的概率低于同色玩家,故基本給對方制造條件,讓對方盡早達到目標,除非能在明牌中一眼看出我可以達成目標(11-S)。顯然,他擬采用的是4?4?2?策略。

第二,通過揣摩對方的行為模式,適時調整配合策略。有玩家通過觀察,確定了“被動”配合策略：多做幾局就發現他比較喜歡先把草花 4換成紅的,如果我的第一張牌不是 2,我會先換它成草花 2或者紅 2,如果我手上是這張牌,一般都懶得換,直接等對手換到合適的牌(25-S)。還有玩家描述了自己復雜的推理過程：通過同色玩家出的第一張牌,來暗示“目標位置”是用同色完成,還是同點完成,這就需要同色玩家先有計劃,哪種方法用的步驟最少。然后同點玩家要通過同色玩家的換牌推測他的計劃,確定誰來完成最后一步,誰來做輔助(32-S)。

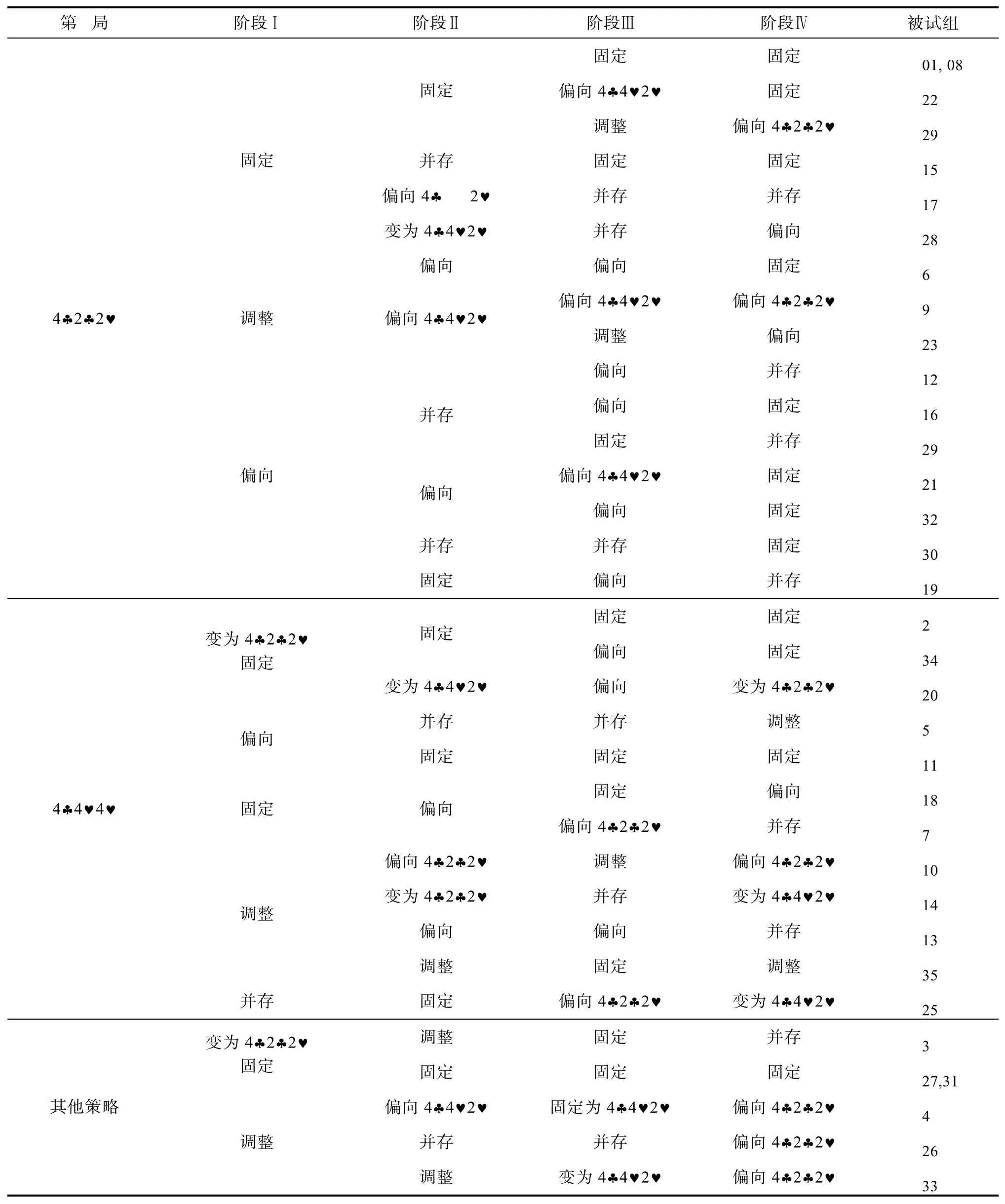
表7 35組被試在四個階段所用策略的變化模式

第三,過牌(P)的暗示作用。有玩家通過過牌暗示對方自己手里有關鍵牌,讓對方配合自己：如果我手里有紅 2,我會不換牌,暗示讓對方換紅牌到目標位置玩家(03-S)。還有玩家通過觀察牌面變化和反應時間推測對方過牌的原因：如果看到牌沒有什么變化,說明紅二已經出現。這個時候,如果同伴點了對手繼續,那自己就知道該怎么做了(04-D);如果對家一直“過”(很快地輪到我)這就說明,他手中有目標位置的牌了。

第四,通過明牌(U)提示對方,進行無聲交流。如同點玩家07-D這樣處理關鍵牌：如果手上有紅心2但是自己又不能達到目的,就放在亮牌位置,方便對方換取,完成任務。又如13-S的描述：如果一方拿到目標牌暫時無法實現任務時,就把目標牌放在名牌的位置,看誰更快完成誰就先拿目標牌。編號為12-D的被試沒有關鍵牌時也會采用這種方法：開始的時候,我們會先換明牌,以讓對方了解自己手中的牌。

(2)策略變化或配合不當的原因

第一,規則的熟悉及熟練應用需要時間。開始幾局,有玩家對自己的身份特點應用不熟練：游戲開始幾道題不是很默契,總是忘記自己扮演的角色(10-D);也有玩家總是控制不住競爭的心理：剛開始的時候總覺得我和同伴是競爭對手的關系,沒有相互配合。這正如某玩家(09-D)的總結：這是一個必經的過程,我覺得這個測驗分為三個階段,首先是熟悉游戲和探索配合方法,然后再去尋找策略,最后基本穩定。

第二,過于“理性”導致的配合不良。許多玩家會按照初始牌局特點,設想不同境況下的不同反應,如對方不能跟上自己的節奏就會出現配合不流暢的情況。如編號為04—S的玩家描述了4種情況下該如何反應：誰手里有紅桃2的話就先不走,手里沒有紅桃2的人就盡量給對方做牌,把目標位置換成對方能換的牌,然后讓對方來走。如果這兩點都不符合的話就換兩張暗牌。如果出現了不太配合的情況就把紅桃 2換到明牌上,作為一個提示,告訴對方手里是什么牌,這樣就可以形成配合了。

第三,雙方想法不匹配。有的是“太想配合”而導致的“不配合”：我們沒有形成固定的策略,有時都想給對方提供換牌的可能,結果弄巧成拙(12-S);有的是對雙方的分工有不同理解,如08-S所述：雙方需要在游戲當中形成分工,一個人做牌(注：將目標位置換成 2?或 4?),一個人胡牌(注：用 2?換牌)。但是同色應該比同點容易胡牌,但我的隊友好像沒太意識到,總在等著我給他做牌。還有對雙方地位的定位存在偏差：開始時,主動置換明牌的一方,是有策略、在合作中居于領導和主動地位的,另一方就是跟隨者,這樣就容易合作。如果雙方在合作中爭奪主導權,會走很多冤枉路(12-D)。

4 討論

4.1 TTT撲克牌游戲為依托的兩人問題解決中的慣例現象

慣例這一概念源于組織、管理和經濟學文獻(Becker,2007;March &Simon,1958;Nelson &Winter,1982;Stene,1940),可以視為一種群體思維定勢(Cohen &Bacdayan,1994)。本研究在重新設計的40局TTT撲克牌游戲中,證明了這一現象的普遍性。

研究首先采用事前事后設計和分析的思路探討了前后 5局模板上被試組表現的差異,這相比Egidi(1996)的研究將5局重復模板放到40局的中間且未對結果進行數據分析,是一種改進。研究發現,經過30次重復性解決同一類問題,被試組在同一模板上問題解決的效率以及所應用的策略均發生了變化(圖4)：第一,對每個模板上前后5局的對比表明,在每局的得分、所用步數和步時上,前后5局的差異在模板2、3、4上比較明顯;在平均步時上各個模板上差異均非常顯著。這主要是因為模板1和 5相對簡單,不論是否形成慣例,只要理解了游戲規則,完成并不難。平均步時這一指標對問題解決效率的體現更為明顯,它反映的是被試進行每一步換牌的思考時間。如果已經形成慣例,雖然完成每局所用總時間上可能變化不大,但每一步動作的目的性會更明確,因而,降低的幅度也最明顯。第二,將前后 5局各視為一個整體,對比其各項指標前后5局的差異后發現,在反映問題解決效率的各項指標上,均是后5局好于前5局,具體體現為總得分的增加、完成每局總時間的減少,和完成每步總時間的減少,但在完成每局的總步數上卻無顯著差異。這說明,問題解決效率的提高,集中體現于獲益和問題解決的速度上,對于所付出的努力,即步數不敏感。在策略的變異上,研究發現其主要體現在其他策略運用的減少上。這說明被試組問題解決過程中,逐漸變得更為理性,不再采用次優策略,轉而探索最佳策略。

對慣例的驗證和描述研究借鑒并完善了前人的指標：(1)可靠性的增加。 這代表了問題解決質量的提高。首先,為方便理解,本研究改變以往用四分位差作為衡量指標的做法(Cohen &Bacdayan,1994),直接用玩家完成每局游戲所用步數和被試組每局游戲得分作為衡量指標。通過這兩個指標的刻畫發現,被試組在重復解決問題的過程中,其可靠性逐漸增加,說明了慣例存在的可能。這是因為慣例的作用之一是節省認知資源,它的出現會使行為越來越自動化,進而空出更多的認知資源進行高水平的思考和更加復雜的決策(Becker,2008)。(2)速度的提高。它是問題解決效率提高的時間指標。本研究對其進行了兩處修正：第一,研究用被試完成每局游戲的總時間(由電腦自動記錄)代替以往研究(Cohen &Bacdayan,1994)采用各組完成每局游戲所用的平均時間(需事后計算)。這樣,通過采用原始數據不僅增加了研究的生態效度,還使數據處理簡潔化。第二,研究增加了平均步時這一指標。不同局甚至同一局游戲都可以用不同的步數來完成,每一步換牌時間直接體現了個體的思考時間,慣例的存在會使思考解決方案的時間縮短(Betsch,Fiedler,&Brinkmann,1998;Betsch,Haberstroh,&H?hle,2002)。分別以上述兩個指標為因變量,以局數為自變量的回歸分析結果均表明,隨著局數的增加,被試組完成每局游戲,及每步換牌所用時間均隨著局數的增加而減少,即問題解決的效率在提高。(3)重復行動序列的存在。這一指標以往只限于描述且僅列舉了 UU*T策略(Cohen &Bacdayan,1994),本研究不僅總結了被試組在重新設計的TTT撲克牌游戲中其他的模糊行為模式;還總結了完整的行動序列。研究表明(表2),通過重復地解決同一類問題,被試組形成了慣例,其集中表現在換右上位置的牌(C)和明牌(U)上。由事后訪談可知,明牌是被試在慣例形成中為與對方進行配合而有意采用的方法。但換右上位置的牌則可能源于游戲中因不斷進行推理和邏輯分析而更多應用大腦左半球的無意識行為,這可由隨著被試意識性的增加其應用次數顯著減少來證明(圖7)。(4)偶爾的次優性。以往研究(Cohen &Bacdayan,1994)對此或進行進行簡單陳述,或直接不分析(王建安,張鋼,2008),本研究通過個案剖析形象說明了慣例的頑固性。(5)基于特定策略的反應模式。與之前預期相一致,本研究發現,被試組在完成任務過程中主要采用了兩種最佳策略,這說明慣例不僅表現在行為層面,更表現在認知層面。

4.2 問題解決中的慣例的形成：微觀發生視角下的表征重述

本研究表明,被試組通過在不到1小時的時間內重復地解決同一類問題,形成了提高問題解決效率的策略,即慣例。這一過程既沒有反饋,也沒有指導,慣例是如何形成的？顯然,答案只能從重復性問題解決過程本身尋找。研究通過微觀發生法的分析表明,慣例的形成表現為策略及行為的不斷變化和調整,即認知表征由無意識走向意識,由程序性轉向陳述性知識。這一過程符合表征重述理論的假設(Kamiloff-Smith,2001),可突出表現為兩個階段：

第一,行為掌握階段,它包括表征水平I。由表4可知,階段Ⅰ中被試組每局得分、步數、每局用時、每步用時均與余3個階段差異顯著,但3個階段之間差異不顯著。這符合Kamiloff-Smith(2001)關于表征水平 I是成功取向的假設,被試通過調整行為和策略以提高問題解決效率。通過表5及表6的分析可知,這一過程行為的掌握是突變的,因為本階段的各項指標及所采用策略只與相鄰的階段Ⅱ差異顯著,與其他階段的差異均不顯著。然而,本階段被試問題解決效率的提高并不意味著慣例的形成。例如,雖然階段I時有16組被試固定了策略,但后續階段他們并未堅持這些策略,而是不斷對其進行調整(表7)。

第二,表征重述階段,包括表征水平 E1、E2和E3。在階段I的基礎上,被試進一步調整和優化自己的行為和策略,使其通達意識。這體現為三階段內各項指標為代表的問題解決效率的緩慢提高(表4),其他策略使用頻率的持續下降(圖6)及無意識行為(換右上位置牌)的逐漸較少(圖7)。與Kamiloff-Smith(2001)通過兒童實驗對三類外顯表征水平的清晰描述不同,TTT撲克牌游戲由于階段Ⅱ和階段Ⅲ被試的意識性無法測量,三類表征只能通過表7所示的各組被試策略使用的變化進行推測。表征水平 E1體現為階段Ⅱ中被試策略的使用更為多變和靈活。例如,階段I中偏向4?2?2?策略的7組被試在階段Ⅱ中有4組兩種策略并存,而并存體現了表征之間的相互作用。再如,其他策略的使用率從11%下降為4%(圖6)。表征水平E2體現為階段Ⅲ中策略的使用更為豐富、連貫。例如,階段Ⅱ中兩種最優策略并存的 3組被試在階段Ⅲ時均固定或偏向4?4?2?策略,且其他策略的使用率進一步下降為3%。表征水平E3體現為階段Ⅳ中策略使用的確定性。例如,階段Ⅲ時有12組被試固定了策略,階段Ⅳ有17組被試固定了策略。而且,與前3階段兩最優策略同時增加的趨勢不同,階段Ⅳ中4?2?2?策略增加,但 4?4?2?策略減少。這說明被試對兩種最優策略有意識地進行了選擇。

4.3 慣例的穩定性、意識性及與陳述性知識的關系

本研究采用微觀發生法的設計和分析思路,闡明了慣例從無到有的產生過程,為其意識性、穩定性爭議及其與陳述性知識關系提供了動態解釋。由上述分析可推測：階段I中被試致力于行為的掌握,形成的是程序性知識,慣例在這個過程中是無意識的,也未完全形成;直到階段Ⅳ被試組才形成了問題解決的最優策略,并能用言語報告,即慣例已轉變為陳述性知識。可見,慣例經歷了由陳述性知識變為程序性知識,由無意識轉向意識過程。這說明以往 Cohen和 Bacdayan(1994)所述的慣例是作為程序性知識進行存儲的觀點并不全面,慣例應是程序性知識與陳述性知識的結合。另外,從微觀產生過程來看,慣例是不斷變化(表7)的,會存在策略的調整、并存、偏向和固定幾種狀態。

上述解釋與慣例生成觀的描述不謀而合,本研究為其提供了實驗支持。Feldman和 Pentland(Feldman &Pentland 2003;Pentland &Feldman,2005;Pentland et al.,2012)認為,慣例包含形式面和執行面兩部分。前者說明慣例由什么組成和用來做什么,具有原則性;后者涉及組織慣例的具體化,指特定人在特定時間和地點參與特定組織慣例活動的真實行為。在任何實際的情境中,慣例的兩個方面均由各種載體承載或驅動。在 TTT撲克牌游戲為載體的慣例中,作為抽象面,形式面不僅如前人所述(Becker,2008)存儲于程序性記憶中,本研究證實,它也存儲于陳述性記憶中。從慣例的微觀產生過程來看,行為的掌握相當于慣例的執行面,而慣例形成的最終階段則相當于形成了慣例的形式面。這一過程與以往研究者所述一致(Feldman &Pentland,2003;Pentland &Feldman,2005),體現了變化性與穩定性的統一：形式面作為目標在還沒有達到或未達到理想狀態時,會一直保持穩定;這時,執行面為了與其保持一致會不斷變化。綜合上述分析,當以微觀發生的視角重新審視慣例時,慣例的生成觀可重新表述為圖8。

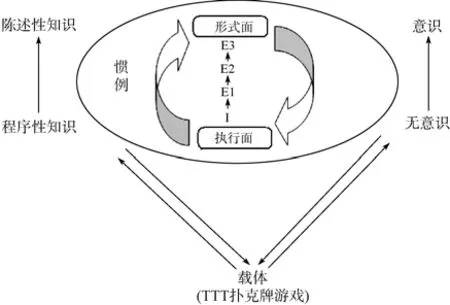
圖8 慣例的新生成觀圖示

由圖可知,慣例由相互聯系和彼此轉化的形式面和執行面組成,并由一定載體承載,其形成體現為由執行面通過表征水平I至E3的重述而通達形式面,并經歷由程序性向陳述性知識以及由無意識向意識的轉化過程。這從慣例產生過程的角度細化了生成觀的表述。

Becker,M.C.(2007).Routines-Abrief history of the concept.In S.Ioannides,&K.Nielsen(Eds.),

Economics and social sciences: Boundaries, interaction and integration

.Cheltenham,UK:Edward Elgar Publishing.Becker,M.C.(2008).

Handbook of organizational routines

.Cheltenham,UK:Edward Elgar Publishing.Betsch,T.,Fiedler,K.,&Brinkmann,J.(1998).Behavioral routines in decision making:the effects of novelty in task presentation and time pressure on routine maintenance and deviation.

European Journal of Social Psychology,28

(6),861-878.Betsch,T.,Haberstroh,S.,&H?hle,C.(2002).Explaining routinized decision making:Areview of theories and models.

Theory and Psychology,12

(4),453-488.Bonini,N.,&Egidi,M.(1999).

Cognitive traps in individual and organizational behavior:Some empirical evidence

.CEEL Working Papers 1999-04,Computable and Experimental Economics Laboratory,Department of Economics,University of Trento,Italia.Cohen,M.D.(1991).Individual learning and organizational routine:Emerging connections.

Organization Science,2

(1),135-139.Cohen,M.D.,&Bacdayan,P.(1994).Organizational routines are stored as procedural memory:Evidence from a laboratory study.

Organization Science,5

(4),554-568.De Boer,E.A.,&Zandberg,T.(2012).Decision-making by organizational routines:The influence of agency and personality traits on deviating from formal organizational routines.

Journal of Quality Assurance in Hospitality &Tourism,13

(4),316-325.Egidi,M.(1996).Routines,hierarchies of problems,procedural behaviour:Some evidence from experiments.In K.Arrow,E.Colombatto,M.Perlman,&C.Schmidt(Eds.),

The rational foundations of economic behaviour

(pp.303-333).London:Macmillan.Feldman,M.S.(2000).Organizational routines as a source of continuous change.

Organization Science,11

(6),611-629.Feldman,M.S.,&Pentland,B.T.(2003).Reconceptualizing organizational routines as a source of flexibility and change.

Administrative Science Quarterly,48

(1),94-118.Kamiloff-Smith, A.(2001).

Beyond modularity: Adevelopmental perspective on cognitive science

(X.C.Miu Trans.).Shanghai:East China Normal University.[A·卡米洛夫-史密斯.(2001).

超越模塊性——認知科學的發展觀

(繆小春 譯).上海:華東師范大學出版社.]Kuhn D.,Goh W.,Iordanou K.,&Shaenfield D.(2008).Arguing on the computer:Amicrogenetic study of developing argument skills in a computer-supported environment.

Child Development,79

(5),1310-1328.Labatut,J.,Aggeri,F.,&Girard,N.(2012).Discipline and change:How technologies and organizational routines interact in new practice creation.

Organization Studies,33

(1),39-69.Luchins,A.S.(1942).Mechanization in problem solving:The effect of Einstellung.

Psychological Monographs,54

(6),1-95.Luwel,K.,Siegler,R.S.,&Verschaffel,L.(2008).Amicrogenetic study of insightful problem solving.

Journal of Experimental Child Psychology,99

(3),210-232.March,J.G.,&Simon,H.A.(1958).

Organizations

.New York:John Wiley.Nelson,R.R.,&Winter,S.G.(1982).

An evolutionary theory of economic change

.Cambridge,MA:Harvard University Press.Pentland,B,T.,&Feldman,M.S.(2005).Organizational routines as a unit of analysis.

Industrial and Corporate Change,14

(5),793-815.Pentland,B.T.,Feldman,M.S.,Becker,M.,&Liu,P.(2012).Dynamics of organizational routines:Agenerative model.

Journal of Management Studies,49

(8),1484-1508.Salvato,C.,&Rerup,C.(2011).Beyond collective entities:Multilevel research on organizational routines and capabilities.

Journal of Management,37

(2),468-490.Stene,E.O.(1940).An approach to a science of administration.

The American Political Science Review,34

(6),1124-1137.Wang,J.A.,&Zhang,G.(2008).Knowledge,routines and performance in collective problem solving.

Acta Psychologica Sinica,40

(8),862-872.[王建安,張鋼.(2008).集體問題解決中的知識、慣例和績效.

心理學報,40

(8),862?872.]Wang,J.A.,&Zhang,G.(2010).Cognitive representations,behavioral routines and dynamic capabilities in collective problem solving.

Acta Psychologica Sinica,42

(8),862?874.[王建安,張鋼.(2010).集體問題解決中的認知表征、行為慣例和動態能力.

心理學報,42

(8),862?874.]Xin,Z.Q.,&Lin,C.D.(2002).The microgenetic method:Focusing on cognitive change.

The Advances in Psychological Science,10

(2),206?212.[辛自強,林崇德.(2002).微觀發生法:聚焦認知變化.

心理科學進展,10

(2),206-212.]