基于LMI和BMI的多時滯不確定離散系統穩定性凸優化算法
陳炎龍,段紅玉
CHEN Yan-long,DUAN Hong-yu
(河南牧業經濟學院 信息工程系,鄭州 450011)
0 引言
實際控制系統中產生的不確定性和時滯會降低系統的穩定性,這使得近十年來不確定時滯系統魯棒控制研究倍受關注[1~3],在不確定離散多時滯系統的穩定性研究和成本界方面也取得了一些成果[4~6]。然而,基于LMI的不確定多時滯離散系統穩定性和可保成本方面的研究較少。最近,文獻[7]利用線性矩陣不等式(LMI)解決了一類帶有單輸入輸出時滯不確定系統的保成本控制,文獻[8]推廣了這一系統,獲得了多時滯離散系統穩定性和可保成本的新LMI方法。真對文獻[8],本文研究了基于LMI和BMI的多時滯不確定離散系統穩定性凸優化算法,以提高可保成本控制水平和獲得較小下界。
1 相關基礎知識
以如下不確定多時滯離散系統為例[8]:


針對系統(1),選取Lyapunov函數為:

其中,P>0,Si> 0, Tj >0。
定義1 對系統(1)和成本函數(2),如果存在狀態反饋控制器u?(k)和正數J?,使得閉環系統(3)漸進穩定,且J ≤J?,則稱J?為可保成本,u? (k)為保成本控制律。
引理1[8]給定矩陣D,E 和維數適當的對稱矩陣G,對滿足FT F ≤ I的矩陣F,不等式G+DFE+ETFT DT <0成立的充要條件是存在實數e>0 使得G+eD D T+e?1ET E<0。
2 所提系統穩定標準

則系統(3)是漸進穩定的,且可保成本:

證明 由公式(4)的Lyapunov函數V(x(k))沿公式(3)系統任意軌線的向前差分為:

令,η(k)=(xT(k),xT(k?τ))T,將公式(7)中
i第二項改寫為:

因此:

根據Lyapunov穩定理論,公式(3)的系統是漸進穩定的。
不等式(8)表明:

上式可以改寫成:
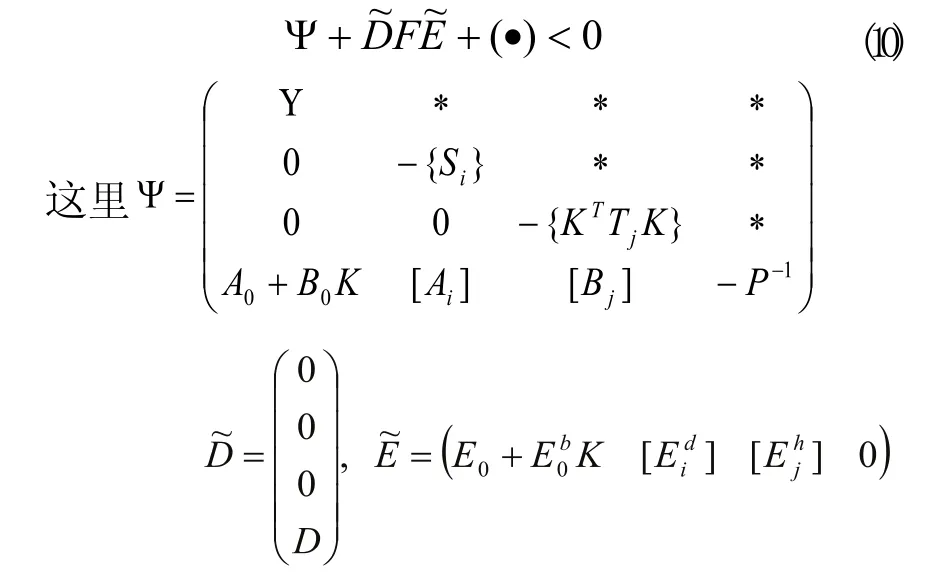

據引理,公式(10)成立當且僅當存在實數e >0使得下式成立:式(12)邊同時乘以diag(X,{X m },{X n },I,I),再次利用Schur complement引理,公式(12)與公式(5)等價。而且,由公式(7)式得到:

將公式(13)兩邊從0到∞求和,結合系統穩定性,就有:

3 所提相關凸優化算法

注3:本算法依賴于初始可行解,在不等式(6)有可行解得情況下,算法可能求不到解.但是如果初始可行解滿足算法,由于它考慮解的迭代搜索,使得獲得的近優解具有較少的保守性。
4 實例驗證
考慮不確定多時滯離散系統[8]:

K=(?0.0363,?0.0459,?0.0132).相應于(6)式的可保成本J *=16.5445,小于文獻[8]中的J *=18.5931。
5 結束語
本文研究了多時滯不確定離散系統的穩定性,給出了一個系統穩定定理,并基于LMI和BMI,提出了一個相關穩定性凸優化算法,同文獻[8]的方法相比,本文優化算法能夠獲得較小的可保成本。
[1]K.Ramakrishnan,G.Ray.Robust stability criteria for a class of uncertain discrete-time systems with time-varying delay[J].Applied Mathematical Modelling,2013,37(3):1468-1479.
[2]Duyu Liu,Shouming Zhong,Xinzhi Liu.Stability analysis for uncertain switched neutral systems with discrete timevarying delay:A delay-dependent method[J].Mathematics and Computers in Simulation,2009,80(2):436-448.
[3]吳江江,余世明.一類不確定多時滯離散系統的穩定性分析與魯棒控制器設計[J].自動化技術與應用,2010,29(1):1-3.
[4]羅躍生,龔新平,李彤.離散多時滯系統時滯記憶魯棒H∞容錯控制[J].華中科技大學學報(自然科學版),2011,30(11):61-67.
[5]Z.Q.Zuo.Y.J.Wang.Novel Optimal Guaranteed Cost Control of Uncertain Discrete Systems with Both State and Input Delays[J].Journal of Optimization Theory and Appli cations,2008,139(10):159-170.
[6]Zhang,Tang.Output feedbackH∞control for uncertain piecewise linear systems[J].Journal of Dynamical and Control Systems,2008,l4(1):141-144.
[7]李陽.多時滯離散系統的反饋控制器設計[J].科學技術與工程,2012,12(31):8434-8437.
[8]楊曉娜,吳華濱,林小峰.基于HDP的離散多時滯系統的優化控制[J].計算機測量與控制,2013,21(2):388-290.

