CORDIC 算法在正余弦函數中的應用及其FPGA 實現

常柯陽，曾岳南，陳 平，覃曾攀

廣東工業大學 自動化學院，廣州510006

1 引言

正余弦函數在眾多工程應用的場合非常廣泛，就典型的采用空間矢量控制方法的電機控制系統來說，坐標變換模塊就需要正余弦函數的實時參與。而在電機控制芯片的發展方面，現場可編程邏輯器件（FPGA）[1]以其速度、靈活性、可靠性和集成度而逐漸受人矚目。

由于計算精度與存儲容量的突出矛盾[2]，在存儲資源有限的FPGA 芯片中，常用的查找表方法沒有優勢；而CORDIC 算法，僅需通過移位與加減運算和占用少量的存儲資源，因此能夠方便地在硬件中實現。但該算法過程復雜，迭代次數較多，輸出時延較長，占用的硬件資源較多。因此，本文提出了一種查找表與CORDIC 相結合的算法，結合兩者的優勢，在保證精度的前提下優化了算法的輸出時延和資源消耗，并在QuartusII 7.2 開發環境下完成了算法的設計、仿真和硬件測試。

2 查找表法和傳統CORDIC 算法介紹

2.1 查找表算法原理

查找表算法的原理是根據計算精度要求，先把一個周期內的正余弦函數分為若干個點，分別求出對應點的函數值，并將結果寫入芯片存儲器中。然后，再通過適當的運算將輸入角度與存儲器地址對應起來，從而查表獲得結果。

用查找表[2]方法實現函數的計算，雖然沒有輸出時延，但其精度和表的容量是指數關系的，就勢必需要大規模的ROM，這在實際應用中需要占用大量的片上資源，甚至是不可行的。

2.2 CORDIC 算法原理

坐標旋轉數字計算機CORDIC（Coordinate Rotation Digital Computer）算法，是由Volder[3]于1959 年提出的，其基本思想是通過一系列與運算基數相關的角度的不斷偏擺，從而逼近所需旋轉的角度。在圓周模式下，其基本實現形式有兩種：旋轉計算模式和向量計算模式。計算正余弦函數時，需采用旋轉計算模式。在文獻[2]中，給出了其基本形式：

其中，xn、yn、zn是當前迭代變量；xn+1、yn+1、zn+1是下一次迭代變量；是符號函數；n是迭代次數。輸入，則輸出為，其中設增益因子，在n→∞時，K≈0.607 253。算法的角度覆蓋范圍[4]為(-99.88°～99.88°)。

3 改進型CORDIC 算法

3.1 改進型CORDIC 算法的思想

由上述算法描述可知，CORDIC 算法結構僅需要移位和加減運算，以及n-1 個旋轉常量，非常方便在FPGA 中實現。但其迭代次數較多，輸出時延大，占用硬件資源較多。考慮到上述因素，本文提出了一種改進型CORDIC 算法，將查找表方法與傳統CORDIC 方法相結合。這樣，可以利用少部分的存儲資源，也能降低迭代次數，節約了硬件資源和降低輸出時延。文獻[4]雖然提出了這種思想，但并未給出具體的實現方法。

CORDIC 算法是一種逐次逼近的算法：以一個初始向量為出發點，按照一定的逐漸減小的角度值上下擺動，最終逼近真實值。傳統的CORDIC 算法，初始向量為X軸，并依次以45°(arctan 20)、26.57°(arctan 2-1)…進行旋轉。

如圖1，在不考慮增益因子的情況下，待求向量d需經過2 次逆時針旋轉和1 次順時針旋轉到達臨近向量c。

圖1 CORDIC 算法角度逼近示意圖

但如果能夠知道待求向量d的范圍在向量b和c之間，并確切知道c的位置，就可以省略a、b和c三次旋轉。對于流水線型結果來說，就可以省略幾級流水線；對迭代式結構來說，就可以減少迭代次數，同時降低輸出時延。正如圖2 中所示，若已知向量d所代表的初始向量對應的坐標為(xi,yi)，則可以省略掉前面0～i次運算，僅需要i～n次的運算。與傳統算法相比，減少了i次運算，因此能夠將輸出時延降低i個時鐘，并降低一部分硬件資源。但同時，由于要獲取初始向量d的坐標信息，相對于傳統CORDIC算法，需要占用較多的存儲資源，其多少取決于算法的運算次數和精度；但相對于查找表方法[4]，其占用的存儲資源則要少很多。也就是說[4]，改進型CORDIC 算法就是解決了查找表算法占用存儲資源大與傳統CORDIC 算法輸出時延大之間的矛盾；在占用有限存儲資源，保證計算精度的情況下，減小了輸出時延和硬件資源。

圖2 改進型CORDIC 算法結構圖

3.2 改進型CORDIC 算法的FPGA 實現

算法實現結構主要分為三個模塊：預處理模塊、初始向量查找表模塊和算法主體及后處理模塊。

整個設計過程是在QuartusII 7.2 環境下實現，采用VHDL 語言與.bdf 原理圖編寫；設計文件內所有數據均采用Q14 格式；而函數floor()表示向負無窮舍入，round()表示向最接近的整數舍入。各模塊的作用如下所述。

3.2.1 預處理模塊

主要作用：擴展輸入角度范圍，并獲得初始向量查找表地址和剩余需旋轉角度。

上文中提到CORDIC 算法的輸入角度覆蓋范圍為(-99.88°～99.88°)，所以在計算前，需將輸入角度范圍擴大為[0 ～2π)。這里對輸入角度theta取其對的標么值，如表1 所示。

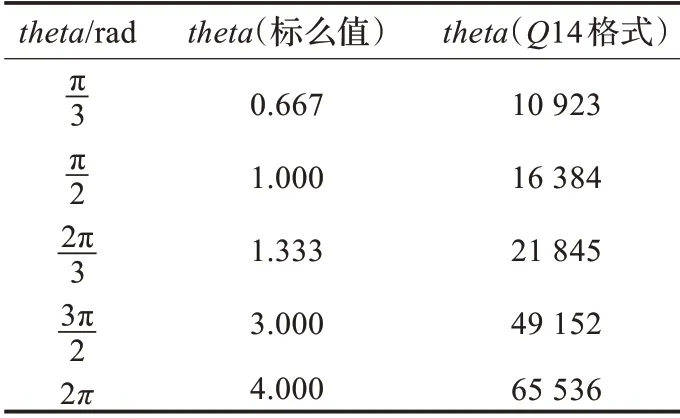
表1 輸入角度數據格式

擴展處理方法的偽碼如圖3。圖中，theta_m為處理后的輸出角度數據，其范圍為；verf為theta的象限狀態值，用于主體算法完成后的后處理；addra為余弦查找表地址，范圍為[0 ～255]；addrb為正弦查找表地址，范圍為[0 ～254]。

設計中，初始向量正余弦查找表由一塊ROM 存儲，地址范圍為[0 ～255]，存儲數據為故。在硬件實現時，僅需將theta_m右移6 位，而；仍需旋轉的角度z=theta_m-(addra+1)×26。

3.2.2 初始向量查找表模塊

模塊功能：根據輸入地址查找相應的正余弦值。

利用宏功能模塊生成兩輸入兩輸出的ROM 模塊，其容量為16 bit×256 word。相鄰兩地址所代表的角度差的標么值的Q格式為

3.2.3 算法主體及后處理模塊

模塊功能：計算輸入角度theta_m的正余弦值，并根據輸入象限狀態verf對輸出結果進行調整，最終得到初始輸入角度theta的正余弦值。

流水線級數的確定：角度旋轉常量如表2。

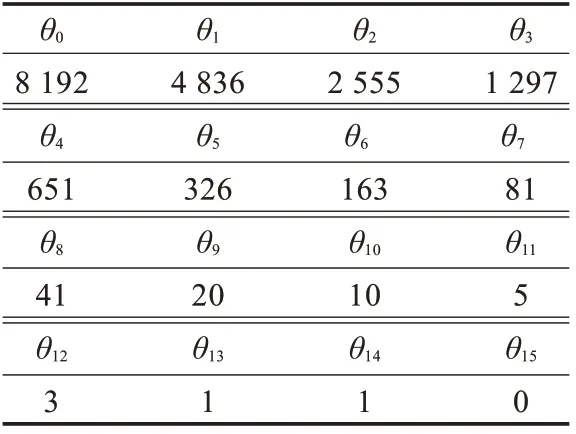
表2 角度常量θi=round(arctan(2-i)×214)

故按照傳統的CORDIC 算法需要15 級流水線。而由于，故采用改進型算法后，僅需8 級流水線，即在初始向量的基礎上擺動8 次就可逼近待求向量。由2.2 節可知，調整因子，文中忽略不計。

后處理部分，是根據verf 進行角度theta 的象限判定，并據此修改輸出結果。

將上述三部分連接，即可得到改進型CORDIC 算法（圖4）。

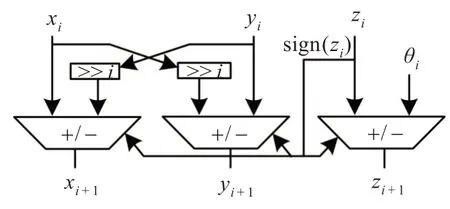
圖4 改進型CORDIC 算法的基本單元

4 仿真結果

在QuartusII 7.2 開發環境下對上述設計文件進行仿真。圖5 給出了傳統算法與改進后算法的仿真結果，其中，輸入角度theta是利用Matlab 軟件計算得到的：

Theta涵蓋了[0 ～2π)范圍。傳統算法的輸出結果較改進后算法延遲了7 個時鐘。

圖5 傳統與改進型CORDIC 算法仿真結果對比圖

將兩種算法的仿真數據與Matlab 計算數據作對比，可得[0 ～2π)輸入范圍內的誤差曲線，如圖6 所示，其中，叉號和圓圈曲線分別為余弦誤差和正弦誤差曲線。從圖中可以看出，兩種算法的誤差均在10-4數量級內，改進后算法誤差絕對值的最大值0.000 3較改進前0.000 4降低了約25%。

5 實驗結果

將上述算法編譯下載至Altera 公司CycloneII EP2C70F896C6 芯片。圖7 為編譯后芯片資源消耗的報告，編譯工具為QuartusII 7.2 自帶的；表3 將兩份報告進行了對比。

圖8 顯示了使用嵌入式邏輯分析儀對算法進行硬件測試的結果，系統時鐘為50 MHz，與仿真結果一致。

6 結論

將查找表算法結構和傳統CORDIC 算法結構相結合，提出了一種計算正余弦函數的改進型的CORDIC 算法，并完成了該算法的仿真設計和FPGA 實現。其結果表明本文算法占用的存儲資源比查找表算法少，硬件資源比傳統CORDIC 算法少，但與傳統CORDIC 算法相比，卻實現了同等數量級的計算精度，并減低了將近一半的輸出時延。將仿真和硬件測試結果與Matlab 計算結果進行了對比，驗證了算法的正確性。如果需要更高的計算精度，可以增加算法中計算數據的位寬；而且，精度越高，數據位寬越大，改進后的算法在資源利用方面的優勢就越明顯。

表3 設計資源消耗及輸出時延對比

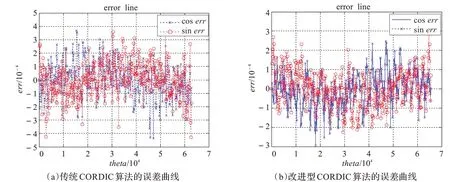
圖6 傳統與改進型CORDIC 算法誤差曲線對比圖

圖7 傳統與改進型CORDIC 算法資源消耗報告

圖8 改進型CORDIC 算法硬件測試結果圖

[1] 劉輝，鄒軒.基于FPGA 和CORDIC 算法的交流電動機直接轉矩控制[J].微特電機，2009，37（8）：57-60.

[2] 吳恒，王淦泉，陳桂林.CORDIC 算法在基于FPGA 的PMSM 控制器中的應用[J].電機與控制學報，2009，13（1）：113-118.

[3] Volder J E.The CORDIC trigonometric computing technique[J].IRE Transactions on Electronic Computers，1959，8（3）：330-334.

[4] 孫宇峰，陳國軍，王大鳴，等.一種高精度正余弦函數的FPGA實現方法[J].信息工程大學學報，2007，8（3）：368-370.