運籌學中關于幾類規劃問題的教學研究

徐 鑫

（安徽大學數學科學學院，安徽 合肥 230601）

1 引言

在經典的運籌學教材中線性規劃、目標規劃以及多目標規劃是分為三個獨立的章節進行教學的，教材中所給出的例題也都是針對這三種規劃問題按照各自章節介紹的方法進行優化和計算，如清華大學版運籌學教材[1]中第一章“線性規劃及單純形法”與第四章“目標規劃”中涉及了許多應用的例子，有生產安排的、有合理利用材料的以及人員分配等例子；而文獻[2-3]也僅僅對目標規劃問題提出不同的優化方法；上述這些文獻僅僅對所研究的規劃問題進行研究，都沒有從這三種規劃的關系角度就探究它們的本質聯系和區別，不具備一定靈活性、系統性；在教學過程中發現學生也只是機械的、單純的會去了解這三種規劃各自概念，然后按照書上給出的例題依葫蘆畫瓢地對相應的規劃問題進行求解，學習過程很刻板，且學習之后也不能很好地將相關章節內容靈活地聯系在一起，達到融會貫通；久而久之，學生不僅對所學內容理解不深刻，而且對相關章節聯系的理解脫節，從而不易提升學生自己對學習新知的能動性、創造性和方法論。因為本文以文獻[1]中例題為引例，結合多年教學過程的經驗和心得來分析三種規劃問題的聯系，并得到有效的結論，為以后的教學創新提供綿薄之力。

2 可化為多目標規劃問題的分析

2.1 線性規劃（LP）與目標規劃（LGP）的研究

2.1.1 引例

以[1]中P102例1為例，題為：某工廠生產Ⅰ、Ⅱ兩種產品，已知有關數據見下表：

?

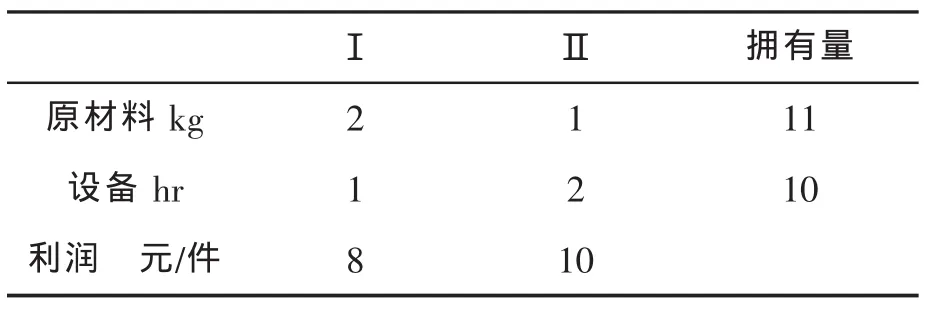
求獲利最大的生產方案。

由例中討論可用如下線性規劃描述

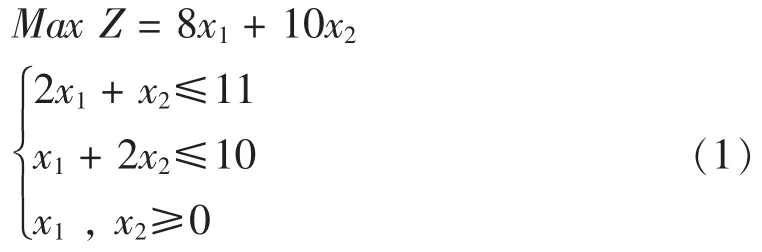
其中X1，X2表示生產產品Ⅰ、Ⅱ的件數。

該工廠的目的是要在不超過所有資源限量的條件下，如何確定X1，X2以得到最大利潤；所以上描述可轉化為目標規劃問題，其描述如下：

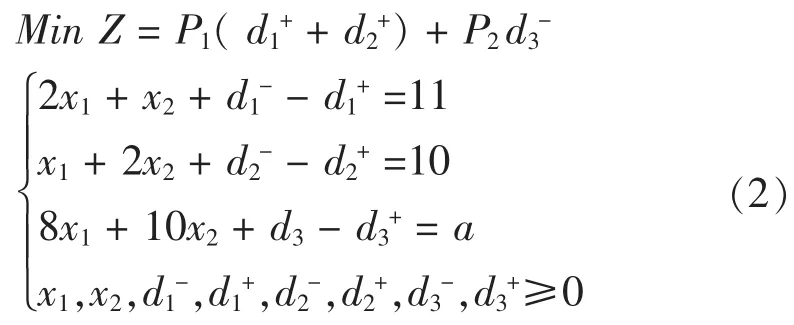
其中a為任一常數。

2.1.2 歸納及分析

我們通過上例得如下歸納：

對標準LP問題：

我們可以將（1）轉化為LGP問題：

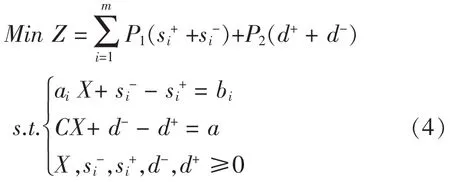
其中 a為任一常數 i=1，2，…，m

也就是說從LGP角度來看（4）式是除去一個目標外，把其余所有目標（在LP里的約束條件）放在等同的優先位置，要求它們必須盡可能地滿足，在此前提條件下，把剩下的一個目標（在LP里稱為目標函數）作為一級考慮因素予以最小化，顯然對于（4）與（3）式并不等價，但作為 LGP模型，（4）敘述更為靈活。事實上LP問題（3）有可行解當且僅當問題（4）第一級目標值為零[4]，這時兩問題的含義是相同的；若問題（3）無可行解，則（4）可以在其特定的算法中找到近似的可行點。

2.1.3 兩種規劃方法比較

一般來說LGP問題比LP問題更具有靈活性，也往往更切合實際。在應用型問題中，經常存在多個目標，這些目標之間可能沖突，可能相互聯系，則此時滿意解往往比最優解更具有現實意義。因為各目標優先級、同級中權系統以及指標值可由決策者提供。所以LGP與LP計算差別不大，同時LGP比LP更易求得結果。不過一旦數據改變，LGP問題也就隨之改變，就得重新計算。

2.2 目標規劃與多目標規劃的研究

上述的引例在實際作決策的時候，要考慮到市場等一系列其它條件，如：引例的決策在原材料供應受嚴格限制的基礎上考慮：首先是產品Ⅱ的產量不低于產品Ⅰ的產量；其次是充分利用設備有效臺時，不加班；再次是利潤不小于56元；求決策方案。

由分析可列得目標規劃為：

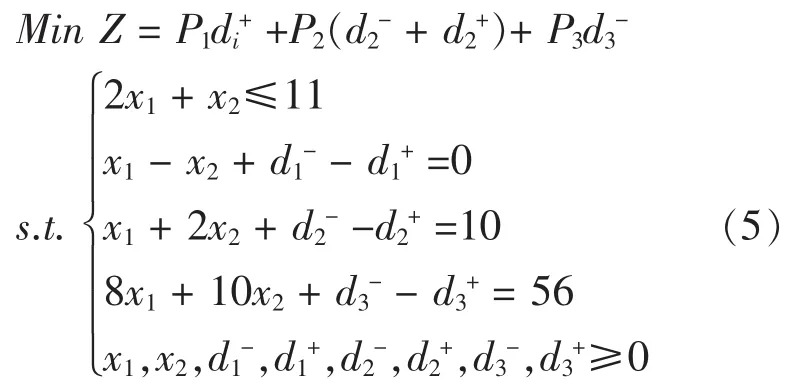
（5）中第一個條件是絕對約束條件，其余的是目標約束；（5）式可轉化為多目標規劃：

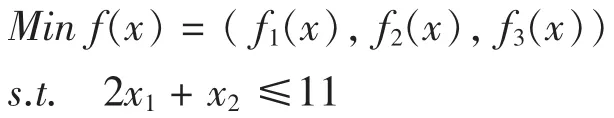
其中

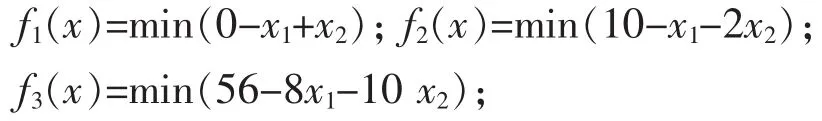
而目標規劃中 P1，P2，P3相當于多目標規劃中的權重，而權重是依實際情況由決策者而定；

我們可將上模型歸納為：

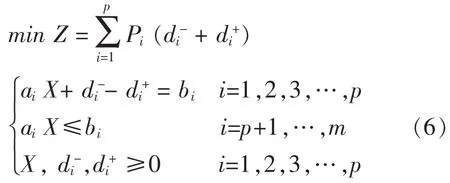
可將（6）式轉化為：

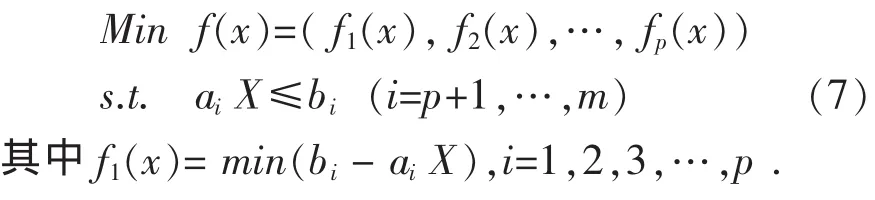
（7）中目標函數中的權重 ω=（ω1，ω2，…，ωm）是由實際因數加上決策者的偏好而定。

2.3 單目標規劃與多目標規劃的關系

線性規劃是屬于單目標規劃問題，但單目標規劃有其自身優點，在解決實際問題中也顯出了其不足之處。在現實生活和實際工作中遇到更為普遍的問題常常含有多個目標，如生產問題中，又想使利潤達到最大，又想使耗電量達到最小等。該問題只用有限個約束條件的單目標規劃是解決不了的，就得依靠多目標規劃進行求解，這就涉及到一個求解多目標規劃問題。多目標解法很多，有TOPSIS法、夾角向量法、層次分析法等等[5]。但要找一種方法把單目標規劃與多目標規劃有機結合在一起的方法——加權和法，見如下定理：

定理 已知多目標決策問題：

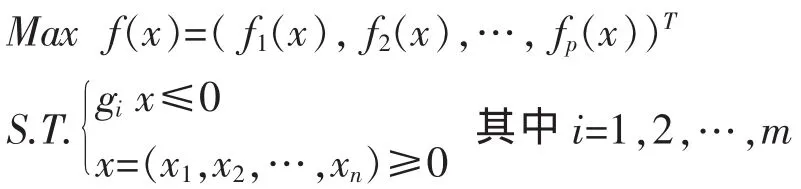
當各目標權重 ω=（ω1，ω2，…，ωp）＞0 時，下列單目標規劃決策問題

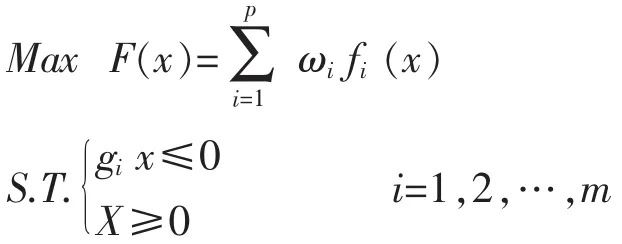
的最優解必為多目標決策的非劣解。

該定理可用K—T條件證明 。

該定理是將多目標規劃轉化為單目標規劃后，用圖象或單純形方法求解，但也有一定的局限性，對于多維情況則很難求解。

3 小結

本文通過對了運籌學中一個經典的線性規劃例子作為引例進行研究，從教學角度對線性規劃（LP）、目標規劃（LGP）及多目標規劃（MLP）這三種常見的規劃的概念、內在關系進行研究，發現在實際中線性規劃和目標規劃都可以轉化為多目標規劃來進行優化，不僅能將這三種規劃融匯貫通理解本質和含義，也為其它規劃問題的拓展研究提供理論和方法上教學借鑒。

從理論上看：線性規劃（LP）、目標規劃（LGP）以及多目標規劃（MLP）三者有著聯系，LGP是LP的推廣，顯然包括LP作為其特殊情況；在LGP中的優先級就相當于MLP中的權重，所以在某種意義上來說，MLP是LGP問題的推廣；所以LP、LGP都可以轉化為MLP來進行求解。

從實踐上看：在日常生活中所遇到的實踐問題中，大多數都涉及到多個目標和要求的，雖然有的可直接用LP和LGP去求解，但LP與LGP所解決的問題多限于一定變量個數，如遇大規模優化問題，LP與LGP解決起來不太靈活；而對于MLP問題求解，我們大多可用軟件來實現，但對MLP求解中，由于權重取的不同，則結果也不盡相同，所以我們可以多取一些權重的形式多進行幾次計算，找一個切合實際的滿意解即可。（因為在解決實際問題中，滿意解往往比最優解更具有現實意義）。

了解的這三種規劃的概念、聯系，也為以后進一步學習隨機規劃、模糊規劃做了鋪墊作用，這些規劃在理論上、方法上都是同出一轍，只是用不同的研究工具對規劃問題進行研究，是的對實際問題的優化問題的研究和討論更加與實際問題跟貼切。

[1] 運籌學教材遍寫組.運籌學（修改版）[M].北京：清華大學出版社，1990.

[2] 錢偉懿，楊菊，等.求解多目標規劃問題的一種新的群體搜索算法[J].遼寧師范大學學報，2007，（2）：141-143.

[3] 劉旺梅，韓旭里.一種求解多目標規劃的新方法[J].系統工程與電子技術，2001，（8）：15-17.

[4] 張建中，許紹吉.線性規劃[M].北京：科學出版社，1999.

[5] 邱箢華.管理決策與應用熵學[M].機械工業出版社，2000.