基于遺傳粒子群算法的飛行沖突解脫

崔莉薇，石為人，劉祥明，吳文政

重慶大學 自動化學院，重慶 400030

隨著民航運輸事業的高速發展，空中交通流量不斷增加，為了改善日益擁擠的空中交通狀況，國際民航界提出了“自由飛行”的概念，所謂自由飛行就是指說駕駛員可以選擇最合適的飛行路線和飛行速度進行飛行。在自由飛行環境下，航路擁擠問題將得到改善，但航路結構限制的取消，使得航空器間沖突問題的解決將變得異常復雜，管制員的工作也將變得更加復雜困難。自由飛行條件下的沖突探測與解脫近年來成為空中交通管理領域的一個研究熱點。

各國的研究人員進行了大量沖突解脫算法的研究工作。ALLIOT[1]論述了基于遺傳算法的解脫方法，該算法可以獲得最短航跡的無沖突飛行方案，但當飛機數目增多時計算比較復雜、耗費時間多。Durand[2]運用簡單的神經網絡來解決兩機間的沖突，可以得到滿意的結果，但當沖突的飛機多于兩架時，神經網絡拓展十分困難，三機比兩機的學習結構適應性差，而且三機以上的拓展使神經網絡的規模增加，學習更困難。Ghosh[3]采用勢能法解決飛行沖突，算法簡單，計算速度快，但該算沒有考慮解脫航跡長度與燃油消耗等因素，且隨著飛機架數的增加，可能會規劃出不適合實際飛機航行的航跡。國內對飛行沖突解脫的研究也取得了一定的成果，嘗試應用了線性規劃法[4]、模擬退火遺傳算法[5]、自適應遺傳算法[6]等方法解決飛行沖突解脫問題，這些方法各有特點，并取得了一定效果。本文在參考國內外有關文獻和的基礎上，采用一種遺傳粒子群算法解決多機的飛行沖突解脫問題，并與文獻[6]和粒子群算法的規劃結果進行了比較。

1 問題的描述與建模

本文根據我國的空管安全規定，對多機沖突解決問題進行簡化[7]：

（1）由于民用飛機一般除了在起飛和降落階段外，都是在固定的高度飛行，且考慮到乘客的舒適要求和燃油消耗要求，飛機之間在改變航路以避免沖突時，只是在水平面內改變方向。因此可以把三維立體問題簡化為二維平面問題。

（2）現實飛行中，民用飛機特別是民用運輸機是一種非高機動性能飛機，且飛機在高空巡航飛行時速度無太大變化，因此假設飛機的飛行速度不變。

（3）按照我國的空管安全規定，當兩架飛機之間間隔大于20 km時不存在飛行沖突。本文為提高沖突識別的準確性，采用10 km作為飛機移動的步長。

（4）民用飛機在巡航階段正常飛行時，一般沒有大角度轉彎或轉向飛行，且固定的航向改變使飛行員能夠更好地執行沖突解決方案，并減少反應時間。這里假設飛機在飛行中任何位置只能選擇3個飛行方向，即保持原有航向、左轉30°、右轉30°。

（5）避免沖突時，通過篩選路徑最短和飛行延誤最小的航路來實現最省油，也最省時。

在以上的前提條件下，假設有N架飛機同時進入一個正方形的沖突區，飛機不作任何航向調整時，保持直線飛行，飛離沖突區的點，稱之為理論上的退出點。算法把飛機在沖突內的飛行時間分為K步，在每一步中，飛機保持一定的航向。在進入每一步時，飛機進行航線調整，以避免發生沖突。

約束條件為沖突區內任意兩架飛機之間的距離D大于飛行安全間距δ：

航線的改變不可避免地會造成飛行路徑長度的增加，飛機飛離沖突區時偏離理論上的退出點。因此，本文的優化目標有兩個，分別是在保證不發生飛行沖突的情況下，使飛機的總航線長度最短且飛行延誤最小（飛行延誤是指每架飛機的理論退出點與實際退出點之間的距離）。

兩個目標函數如下：

其中，Si為第i架飛機在沖突區內飛行路徑的長度，di為第i架在沖突區內的延誤。

本文使用線性加權法確定評價函數，線性加權法是最簡單、最基本，也是應用最廣泛的多目標優化方法。

對每架飛機根據其進入沖突解脫域的入口點，起始航向和每一步的航向變化，計算其整個航跡，并檢查初始種群生成的實驗航跡是否存在飛機沖突。如果發現飛行沖突，該個體的適應值將設置為0。如果沒有沖突，對每一架飛機i,計算其在空域內飛機的總航線長度和飛行延誤，并使用線性加權法確定評價函數。

適應值函數如下：

其中，n為沖突區內的飛機數量，di為第i架的飛行延誤，Si為第i架飛機在沖突區內的飛行路徑長度，k1和k2為常數。

為簡單起見采用二進制編碼，如果在空域里有N架飛機，則將構造一個N×K×2維的解空間，將每個個體對應的解空間，分解成N個K維向量：Xn=( )xn1,xn2,L,xnk(k=1,2,…,K)，表示第k架航班在沖突區內的航線調整。其中：

通過合理的數學建模，將多機的沖突解脫問題簡化為帶約束的整數規劃問題。

2 基于遺傳粒子群算法的飛行沖突解脫

2.1 標準遺傳算法（SGA）

標準遺傳算法（Simple Genetic Algorithm，SGA）是Holland于20世紀60年代提出一種計算模型[8]，它是模擬生物在自然環境中的遺傳和進化過程形成的一種全局優化概率搜索算法。對于一個特定的問題，遺傳算法從代表問題可能潛在解集的一個種群開始，種群由經過基因編碼的一定規模的個體組成，之后按照適者生存和優勝劣汰的競爭原理，在每一代，采納了自然進化模型，根據問題域個體的適應度大小選擇優良個體，并借助自然遺傳學的遺傳算子進行組合交叉和變異，逐代進化以產生代表新的解集的種群。周而復始，反復迭代，直到滿足終止準則，最后將運算結果作為問題最優解。

經過多年的發展，遺傳算法理論逐漸成熟，已經被成功應用于優化設計、模糊邏輯控制、神經網絡、專家系統等領域。

2.2 粒子群算法（PSO）

粒子群優化算法（Particle Swarm Optimization，PSO）是由Eberhart與Kennedy提出的一種新的模擬鳥類捕食行為的全局優化進化算法[9]。該算法首先初始化一群隨機粒子，然后通過迭代找到最優解。在每一次迭代中，粒子通過跟蹤兩個“極值”來更新自己：一個是粒子本身所找到的最優解；另一個是整個種群目前找到的最優解。

粒子群算法結構非常簡單，參數少，只需簡單的數學運算便可以實現，自出現以來受到了廣泛的關注，在組合優化[10-11]、控制器參數調節[12]等領域得到了大量的應用。

2.3 基于遺傳粒子群算法的飛行沖突解脫

PSO與GA有很多共同之處：它們都起源于人類對生物學的研究，屬于仿生計算范疇；都使用適應度函數來評價系統，群體根據適應度值進行復制；兩種算法都經過不斷的搜索，找到最優解。它們又有所不同，遺傳算法具有交叉和變異操作，具有廣泛的空間搜索能力，在搜索過程中不容易陷入局部最優，但是算法復雜，搜索速度慢，沒有種群的移動，缺乏記憶功能，不能參考歷史信息。粒子群算法結構簡單，僅僅根據自己的速度來決定搜索，沒有GA明顯的選擇、交叉和變異操作，具有運行速度快，擁有記憶功能等特點。本文將遺傳算法和粒子群算法相結合，提出一種遺傳粒子群算法解決多機沖突解脫問題。該算法既保持了個體之間信息交流，避免陷入早熟收斂與局部最優，又提高了搜索效率與加快計算速度。該算法步驟描述如下：

圖1 算法編碼機制示意圖

步驟1隨機產生初始種群Pop。算法采用二進制編碼機制，種群中的任意個體Xi的維度為Q,Q=N×K×2,N為飛機數目，K為每架飛機在沖突區內航向調整的次數。編碼機制如圖1所示。

步驟2設定參數，確定遺傳交叉概率pc,變異概率pm,粒子群慣性因子w,加速度系數c1、c2和最大迭代次數NCmax。

步驟3計算每個個體的適應度函數值，采用輪盤賭選擇方法挑選出染色體對，以確定的概率進行交叉和變異操作，得到種群Pop′。

步驟4對Pop′中的個體進行適應度評估，得到個體最優位置pim和全局最優位置pgm,并按照式（5）和式（6）分別對種群速度和位置進行更新，產生下一代種群Pop。

步驟5判斷是否已經達到最大迭代次數，如果到達，結束進程，輸出結果；否則轉至步驟3。

該算法的流程圖如圖2所示。

圖2 遺傳粒子群算法流程圖

圖3 （a）實例1的沖突解脫路徑圖

圖3 （b）1到10步的沖突解脫路徑圖

圖3 （c）11到20步的沖突解脫路徑圖

3 仿真及驗證

在仿真實驗中，4架飛機以相同的速度飛行，把飛機的飛行時間分為20步，如不進行航線調整，在第10步時4架飛機將同時發生沖突。算法中，群體大小設480，對應著480條隨機航路。交叉運算的概率設置為0.7，變異概率為0.01。粒子群的慣性因子w=0.8，加速度系數c1=c2=0.7。

實例1 4架飛機直線交叉通過沖突區，其中A飛機從西向東飛行，B飛機從南向北飛行，C飛機從東向西飛行，D飛機從南向北飛行。

經10次抽樣記錄，此算法平均在運行10次迭代后能收斂于理想的結果，平均耗時為2.31 s。圖3（a）為實例1的沖突解脫路徑，圖 3（b）和3（c）分別為1到10步和 11到20步的解脫路徑。圖4為算法適應度函數值曲線。

圖4 實例1的適應度函數值曲線圖

為了評價本文算法的性能，將該算法所得到結果與文獻[6]中的算法，以及二進制粒子群算法的規劃結果進行了比較。表1列出了三種算法運行結果對比。

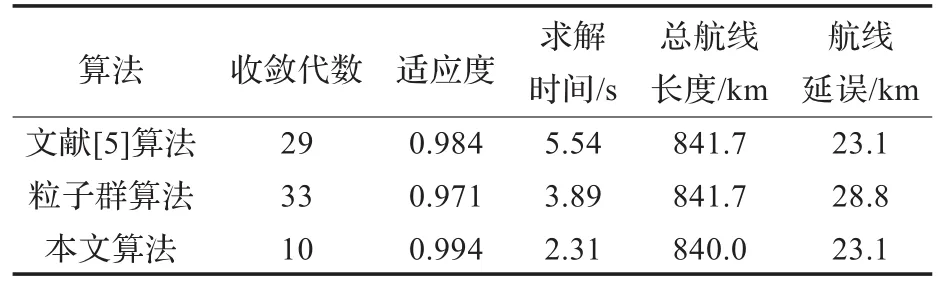
表1 實例1三種算法結果對比

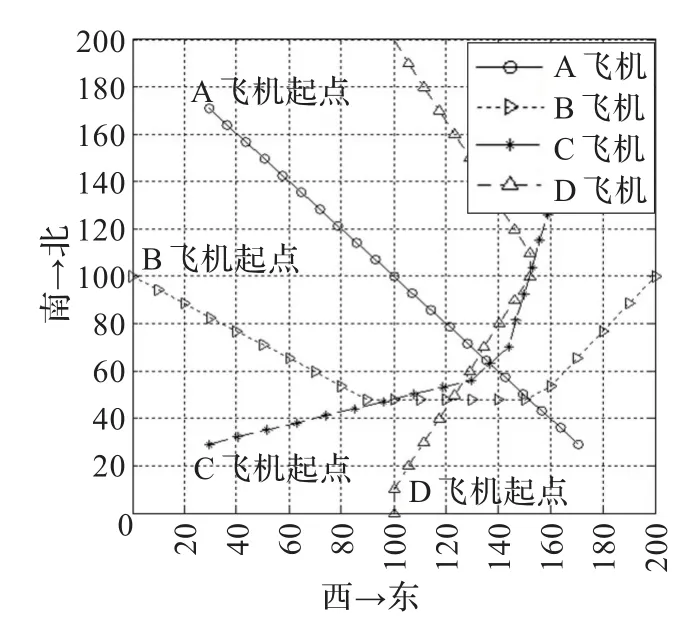
圖5 （a）實例2的沖突解脫路徑圖

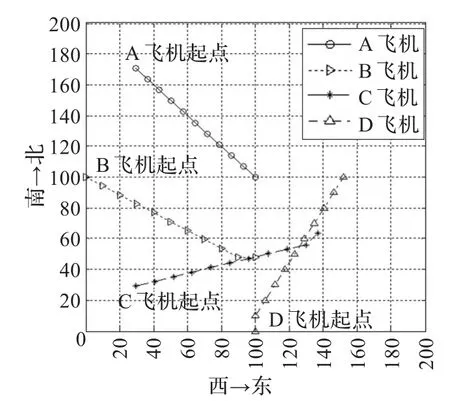
圖5 （b）1到10步的沖突解脫路徑圖

圖5 （c）11到20步的沖突解脫路徑圖

實例2 4架飛機以45°交叉飛過沖突區，每架飛機的起始位置到沖突區的中心的距離為100 km，其中A飛機從西北向東南方向飛行，B飛機從西向東飛行，C飛機從西南向東北飛行，D飛機從南向北飛行。

經10次抽樣記錄，此算法平均在運行29次迭代后能收斂于理想的結果，平均耗時為7.12 s。圖5（a）為實例2的沖突解脫路徑，圖5（b）和5（c）分別為 1到10步和11到20步的解脫路徑。飛機間的安全飛行間距為20 km，圖5中的4架飛機經過20步航向調整后，任意兩架之間的間距都大于安全間距。圖6為算法適應度函數值曲線。

表2為實例2中，本文算法與文獻[1]中的遺傳算法、文獻[6]中的自適應遺傳算法的規劃結果對比。

表2 實例2三種算法運行結果對比

仿真實驗證明，本文算法能夠快速有效地解決同一沖突區內4架飛機的沖突解脫。由表1、表2對比結果可以看出，遺傳粒子群算法在收斂代數和計算速度都優于其他兩種方法，且收斂時的適應度值更高，規劃出的路線更接近原航線，這就減少了飛機的燃油消耗和管制員的工作負荷。實驗證明，遺傳粒子群算法解決同一沖突區內4架飛機的飛行沖突問題效果更好。

4 結論

本文采用遺傳粒子群算法有效地解決了4架飛機的飛行沖突。該算法綜合了遺傳算法的全局搜索能力與粒子群算法記憶功能和快速收斂的特點，計算速度快，搜索效率高，可以在相當短的時間內規劃出飛行解脫航跡，且解脫后的飛機航跡平滑，更接近于原航線。本文假設飛機在固定高度層飛行，將飛行的運動限制在二維平面中，對于三維空間中的沖突解脫問題的研究，將是下一步的工作重點。

[1]Alliot J M，Gruber H，Joly G.Genetic algorithms for solving air traffic control conflicts[C]//Proceedings of the 9th Conference on Artificial Intelligence for Applications，Orlando，FL，USA，1993：338-344.

[2]Burdun I Y.An AI situational pilot model for real-time applications[C]//Proceedings of the 20th Congress on the International Council of the Aeronautical Sciences，Sorrento，Napoli，Italy，September 8-13，1996：210-237.

[3]Ghosh R，Tomlin C.Maneuver design for multiple aircraft conflict resolution[C]//Proceedings of the American Control Conference，Chicago，Illinois，2000，9：672-676.

[4]靳學梅，韓松臣，孫樊榮.自由飛行中沖突解脫的線性規劃法[J].交通運輸工程學報，2003，3（2）：75-79.

[5]裴志剛，李華星，王慶勝.模擬退火遺傳算法在飛行沖突解脫中的應用[J].交通與計算機，2005，23（1）：115-117.

[6]趙源.航路飛行輔助決策仿真系統關鍵問題研究[D].西安：西北工業大學，2005：33-37.

[7]中國民航局.CCAR-91-R2一般運行和飛行規則[S].2007-11-22.

[8]Holland J H.Adaption in nature and artificial system[M].Ann Arbor：The University of Michigan Press，1975.

[9]Kennedy J，Eberhart R C.Particle swarm optimization[C]//Proceedings of IEEE International Conferenceon Neural Networks，Perth，Australia，1995.

[10]陳自郁，何中市，何靜媛.一種求解集合組合問題的離散粒子群優化模型[J].華南理工大學學報：自然科學版，2010，38（4）：141-145.

[11]魏靜黃，王宇平.求解約束優化問題的改進粒子群算法[J].系統工程與電子技術，2008，30（4）：739-742.

[12]Kim T H，Maruta I，Sugie T.Robust PID controller tuning based on the constrained particle swarm optimization[J].Automatica，2008，44（4）：1104-1110.