基于組合預測模型的GDP統計數據質量評估研究
陳黎明,傅 珊
(湖南大學金融與統計學院,長沙 410079)
1 組合預測模型及數據質量評估方法
不同的預測方法根據相同的信息,往往會提供不同的結果,如果簡單的將誤差較大的一些方法舍棄掉,將會丟棄一些有用的信息,使得模型的精度不高。組合預測法是指通過建立一個組合預測模型,把多種預測方法所得到的預測結果進行綜合。由于組合模型能夠較大限度地利用各種預測樣本信息,所以它比單項預測模型考慮問題更系統、更全面,因而能夠有效地減少單個預測模型受隨機因素的影響,可以提高預測的精確度和穩定性[1]。
1.1 單項預測模型
1.1.1 灰色預測模型
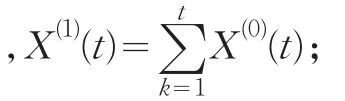
(1)殘差檢驗
按預測模型計算X^(1)(i),并將X^(1)(i)累減生成X^(0)(i),然后計算原始序列X(0)(i)與X^(0)(i)的絕對誤差序列Δ(0)(i)及相對誤差序列Φ(i),一般而言,當絕對誤差序列的數值波動較小且Φ(i)≤5%時,即可認為通過了殘差檢驗。
(3)后驗差檢驗

若所建模型不能通過殘差檢驗,為了提高灰色預測模型的精度可建立殘差GM(1,1)模型,用殘差GM(1,1)模型的修正值加到原預測值上,以補償原預測值。
1.1.2 回歸組合模型
一般而言,反映社會經濟現象的數據序列不平穩,往往呈現出一定的趨勢或者周期性,可以建立非平穩的時間序列模型。觀察GDP數據的時序圖,發現GDP數據確實存在如上的性質。因而可以用以下模型來描述其變化:
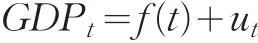
其中f(t)表示GDPt隨時間變化的均值,是序列的確定性趨勢,可以用多項式、指數函數等來描述,ut為GDPt序列中剔除確定性趨勢后的隨機部分,可以看做是一個零均值的平穩過程,用ARMA模型來描述。在實踐中對其通常有兩種處理方法:一是直接建立ARMA模型;二是采用一種組合模型,根據序列GDPt的特點,選取合適的函數形式擬合確定性部分f(t),直到剩余序列ut可以用ARMA模型擬合。該方法即考慮了時間序列變動的確定性因素,又考慮了隨機因素,具有良好的預測效果,本文采用這種處理方式。
1.1.3 雙指數平滑
時間序列平滑預測法,主要通過事物自身的發展變化,借以預測事物的未來發展趨勢。在沒有發生重大的經濟體制轉變時,GDP的發展趨勢可以延伸到未來,故采用時間序列來擬合GDP的發展趨勢是合適的。指數平滑法是對時間序列由近及遠采取逐步衰減的加權處理,當時間序列的變動具有線性趨勢時,采用雙指數平滑來消除滯后誤差。預測步驟如下:
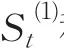
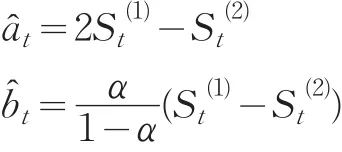
1.2 組合預測模型
權軼和張勇傳(2005)系統分析了組合預測模型的權重確定方法,并對各種權重的模型預測精度進行了比較,證明最優組合綜合模型的精度優于其中任何一個單一模型和其他的組合模型[2]。本文欲通過預測值代替“真值”進行數據質量評估,需盡量提高模型的預測精度,因此選擇使精度達到最高的權重,構建基于誤差絕對值和最小的組合預測模型。

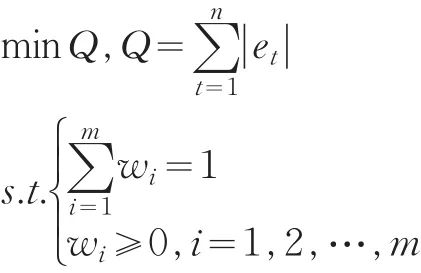
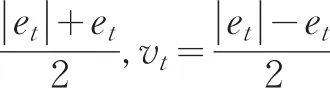
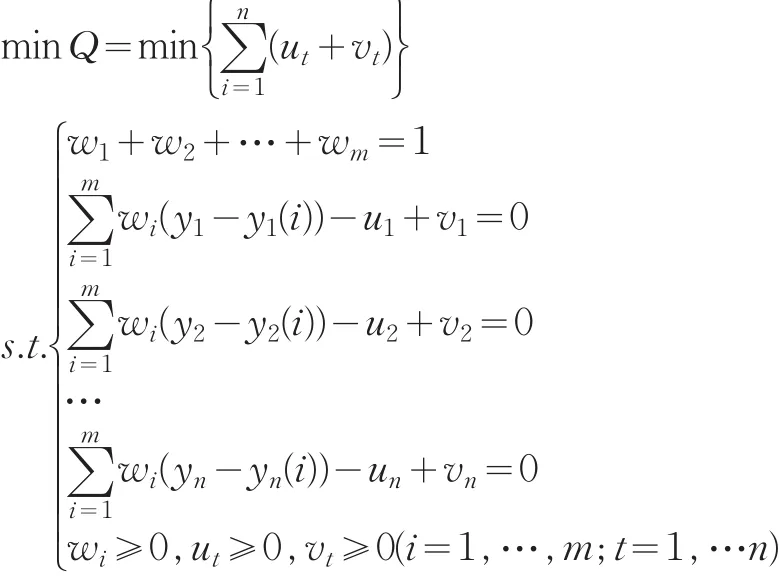
該線性規劃問題有m+2n個未知量和n+1個約束條件,可以利用單純行法進行線性問題的最優解求解[3]。
1.3 數據質量的評估
在估計出具體的評估模型之后,對數據質量評估方法的選擇,本文從檢驗異常值角度分析預測誤差,找出離群值的思想,利用Grubbs準則和Dxion準則檢驗模型預測相對誤差的異常值,進行數據質量評估。值得注意的是,異常值討論的前提是觀測樣本主體(除個別離群值外的大部分樣本值)均來自同一正態總體或近似正態總體,因此,需要事先對觀測樣本進行正態性檢驗。
(1)Grubbs準則
對于服從正態分布的n個相對誤差數據P1,P2,P3,…Pn,按從小到大排序,計算檢驗統計量Gn=P(n)-Pˉ/s,G1=Pˉ-P(1)/s,其中P(n)和P(1)分別為排序后的最大值和最小值,Pˉ和S分別是樣本均值和樣本標準差。在雙側情形下,給定顯著性水平α,若Gn≥G(α,n),Gn>G1,則認為P(n)為異常值;若G1≥G(α,n),G1>Gn,則認為P(1)為異常值。其中G(α,n)是檢驗統計量的臨界值,可通過查表得到。
(2)Dxion準則
對于服從正態分布的n個相對誤差數據P1,P2,P3,…Pn,按從小到大排序,得到順序統計量P(1)≤P(2)≤…≤P(n)。檢驗統計量根據樣本量n以及可疑數值的位置和個數來選取,具體由表1給出:

表1 Dixon檢驗統計量
在雙側情形下,給定顯著性水平α,查Dixon臨界值表對應n的臨界值D(α,n).若D>D',D>D(α,n),則可判斷P(n)為異常值;若D'>D,D'>D(α,n),則可判斷P(1)為異常值;否則,判斷數據沒有異常值。數學證明,在一組數據只有一個異常值時,Grubbs準則優于Dxion準則,當數據存在一個以上異常值時,Dxion準則要優于Grubbs準則[4]。
2 組合預測模型對我國GDP數據準確性檢驗的實證分析
2.1 數據的選取
我國統計部門于1985年才建立GDP核算制度,此后的GDP數據相對之前的數據更可靠。此外,本文是將樣本集即作為訓練集又作為評估集,需要假定樣本集的數據基本可信,因此選擇1985~2010年間的GDP數據作為樣本進行分析,為了剔除價格因素的影響,將其統一換算成1985年的不變價GDP。
2.2 單項預測模型的建立
2.2.1 灰色預測模型
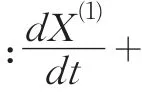
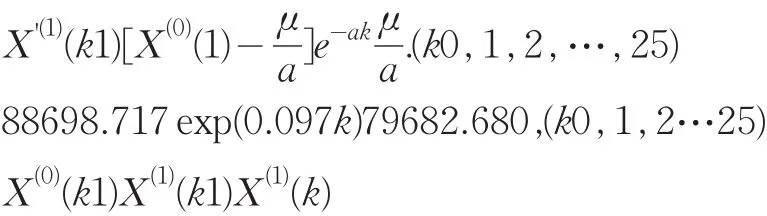
所建模型不能直接用于預測,需進行灰色預測檢驗,檢驗結果如表2所示:

表2 灰色預測檢驗
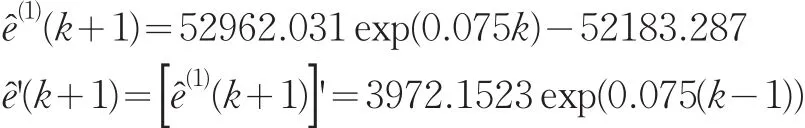

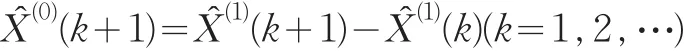
2.2.2 回歸組合模型
(1)對GDP序列確定性趨勢的模擬
對GDP繪制散點圖,通過圖形可以看出GDP數據呈現曲線上升的趨勢,為非平穩時間序列。可以考慮選擇二次曲線模型或者指數模型來擬合GDP的趨勢增長,經過實踐,發現指數模型的預測效果較好,因此,選擇擬合指數模型。
指數模型GDPt=aebt+εt可以通過數據的對數變換化為直線回歸模型,使分析更為直觀和簡便,因此對上式兩邊取對數得到線性回歸模型:lnGDPt=lna+bt+μt,其中t為趨勢項(t=1,2,…,26),采用最小二乘法估計得到如下模型:
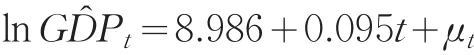
其中,可決系數為0.998,F統計量為9768.744,對應的P值為0.000,在5%的顯著性水平下,回歸方程和回歸系數都很顯著。然而模型的DW值較低,只有0.437,模型可能存在自相關。因此,對殘差序列進行LM檢驗,得到LM檢驗統計量為20.413,相伴概率為0.000088,在5%顯著性水平下,拒絕原假設,即認為模型的殘差序列存在二階自相關,考慮對殘差序列μt建立ARMA模型。
(2)對模型殘差序列μt的模擬
在建立ARMA模型之前先對序列μt進行平穩性檢驗,在5%的顯著性水平下,根據AIC準則選取階數,對殘差序列進行包括常數項和趨勢項的ADF檢驗,得到ADF統計量為-3.658,相伴概率為0.047,小于0.05,拒絕原假設,判定殘差序列平穩,可以建立ARMA模型。通過觀察μt的自相關與偏自相關圖,發現自相關拖尾,偏自相關二階截尾,初步判定μt存在二階自相關,可擬合AR(2),結果如下:
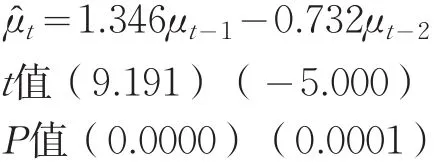
通過該模型殘差序列的自相關和偏自相關分析圖,發現其自相關系數和偏自相關系數都落入了2倍標準差之內,Q統計量的相伴概率都大于0.05,可認為殘差序列為白噪聲序列,說明AR(2)模型的擬合效果較好。
(3)最終回歸組合模型
將模型隨機誤差項μt的滯后項μt-1、μt-2引入原模型,在Eviews軟件中對原回歸方程重新做整體性估計,得到回歸組合模型為:

模型調整后的可決系數為0.999,F值為11892.62,對應的P值為0.000,模型顯著。為驗證模型殘差是否還存在自相關,對模型殘差進行LM檢驗,在5%的顯著性水平下,LM檢驗統計量為1.112,相伴概率為0.292,大于0.05,說明殘差序列已不存在自相關,模型擬合效果較好。
2.2.3 雙指數平滑
由上文可知,GDP序列呈指數形式增長,其對數序列線性增長,為了描述這一特征,將其對數序列進行雙指數平滑,得到平滑預測值,然后取其反對數,即可得我國GDP的預測值。運行Eviews軟件,采用使誤差平方和達到最小的準則對平滑參數進行估計,得到平滑參數α=0.999,殘差平方和為0.015,預測效果較好。
2.3 組合預測模型
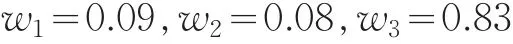
則組合預測模型為:
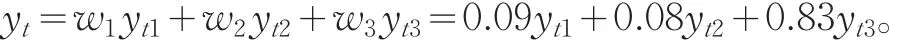
為檢驗組合預測模型的有效性,對所建的三個單項預測模型和組合預測模型進行精度比較,評價指標選用平均相對絕對誤差MAPE,計算結果如表3:

表3 模型預測精度評價結果
由表3可知,組合預測模型的MAPE最小,預測精度最高,利用該模型對我國1985~2010年間的GDP數據進行預測所得的預測值更接近“真值”,數據質量評估的可靠性更高。
2.4 數據質量評估
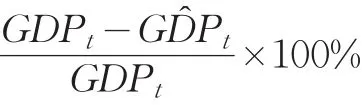
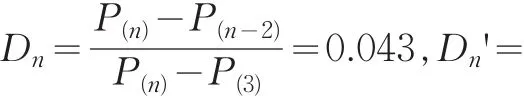
3 結論與評價
從異常值的角度進行數據質量評估,需結合異常值產生的背景進行分析。雖然1989年的GDP數據是異常值,但其異常與其所處的特殊時代背景有關,1988年中國發生了嚴重的通貨膨脹,與上年相比,零售商品價格上升了18.5%,居民消費價格上升了18.8%。全國各地發生了搶購商品潮。政府從1988年的第四季度起實行嚴厲的“治理整頓”,利用各種手段緊縮投資和貨幣投放,使得價格的上升速度迅速下降。但是嚴厲的緊縮也引起了經濟增長速度的迅速下滑,1989年和1990年GDP分別只增長了4.1%和3.8%。這是改革開放以來最慢的增長率。1989年間的GDP數據低于其他年份的數據是可以理解的,但是并不能確定1989年GDP數據的異常是否就是由客觀原因造成的,因此不能直接判斷其準確性,需要進一步研究,只能認為1985~2010年間的GDP數據基本上都是準確的。
利用統計模型對數據質量進行評估,基本思想是用模型的預測值充當“真值”,然后檢驗預測值與評估數據的差異是否顯著,若差異顯著,則數據存在異常值,如果異常值不是客觀原因(如外部沖擊、體制變革等)造成的,即可認為是數據本身的準確性問題。然而根據歷史數據得到的預測值和真實值之間存在一定的差異,要得到更準確的結論,需要采用預測效果更好的模型進行預測,盡可能地縮小這個差異。組合預測模型能將各種不同類型的單項預測模型兼收并蓄,集中更多的經濟信息與預測技術,減少預測系統誤差,顯著改進預測效果。可見,相比單項預測模型,運用組合預測模型對數據的準確性進行檢驗效果會更好。本文以我國1985~2010年間GDP數據的準確性為例進行實證分析,依據考察指標的特點構建了灰色預測模型、回歸組合模型和雙指數平滑模型三個單項預測模型,然后根據組合預測模型的基本思想,將三個單項預測模型的預測值進行加權組合得到組合預測模型。通過對比各個單項預測模型和組合預測模型的預測精度發現,組合預測模型確實優于單項預測模型,所得的預測值更接近“真值”,更適合于數據的準確性檢驗。可見,組合預測模型在統計數據的準確性檢驗中確實存在較高的實用價值,值得進一步研究。
[1]徐國祥.統計預測和決策[M].上海:上海財經大學出版社,2009.
[2]權軼,張勇傳.組合預測方法中的權重算法及應用[J].科技創業月刊,2006(5).
[3]農吉夫,金農,譚福錦,主毅.最優組合預測的短期氣候預報建模研究[J].數學的實踐與認識,2008,38(8).
[4]王華,金勇進.統計數據準確性評估:方法分類及適用性分析[J].統計研究,2009,26(1).

