一種光學元件面形三維重建的算法研究＊

穆 綿，劉纏牢

（西安工業大學 光電工程學院，陜西 西安 710021）

引 言

隨著光學技術的發展，光學元件的應用日益廣泛，因此對光學元件的質量檢測提出了更嚴格的要求。針對市場需要實現非接觸在線檢測的要求，提出一種基于結構光的三維檢測方法，目前這種方法多用于檢測高反射率的物體，因此將此方法運用于檢測光學元件面形是一種新的嘗試。基于結構光的三維檢測方法對于周圍的檢測環境要求較低，可用于工廠實現光學元件面形的在線檢測。

1 測量原理

本文探究的是基于線結構光掃描測量（光切法）［1－2］和立體視覺測量（雙目立體視覺法）［3－4］相結合的一種檢測光學元件面形的測量方法，測量原理如圖1所示。一定模式的結構光投射到被測物表面，相機采集受被測面形調制的光條圖像。

圖1 線結構光視覺法測量原理圖Fig.1 Schematics of line structure light vision measurement

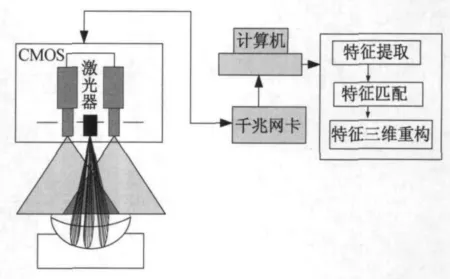
圖2 投影法檢測光學面形的設計方案Fig.2 Design scheme of optical surface characterization inspection by projection method

2 實驗方案設計及圖像采集

根據測量原理，設計投影法檢測光學面形方案如圖2所示。將兩個CMOS相機平行放置，再將線激光器放置在兩個攝像機中間并垂直平分兩相機連線。線結構光垂直水平面投射被測物體表面產生三條亮度很高的細線，左右相機采集到線結構光條的圖像，利用結構光平面標定技術，可以得到光條圖像坐標和世界坐標之間的轉換關系，實現三維坐標測量。

在實驗中，由于客觀條件的限制，采用單線激光器對光學元件表面掃描，電控平移臺每移動0.5mm，相機采集得到一組左右視圖，故實驗過程共采集得到了12組圖片（任選一組左右視圖如圖3所示）。圖4給出了對采集得到的圖片進行軟件編程算法的流程圖。

圖3 原始圖像對Fig.3 Untreated images

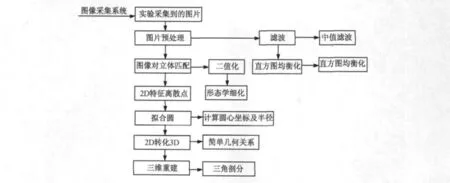
圖4 軟件算法流程圖Fig.4 The flow chart of software algorithms

3 數學模型

3.1 攝像機的成像模型

定義圖像坐標系（u，v）、攝像機坐標系（Xc，Yc，Zc）和世界坐標系（XW，YW，ZW）來描述攝像機成像過程。設原點位于（u0，v0）像素點上，這三個坐標系之間的關系見下式：

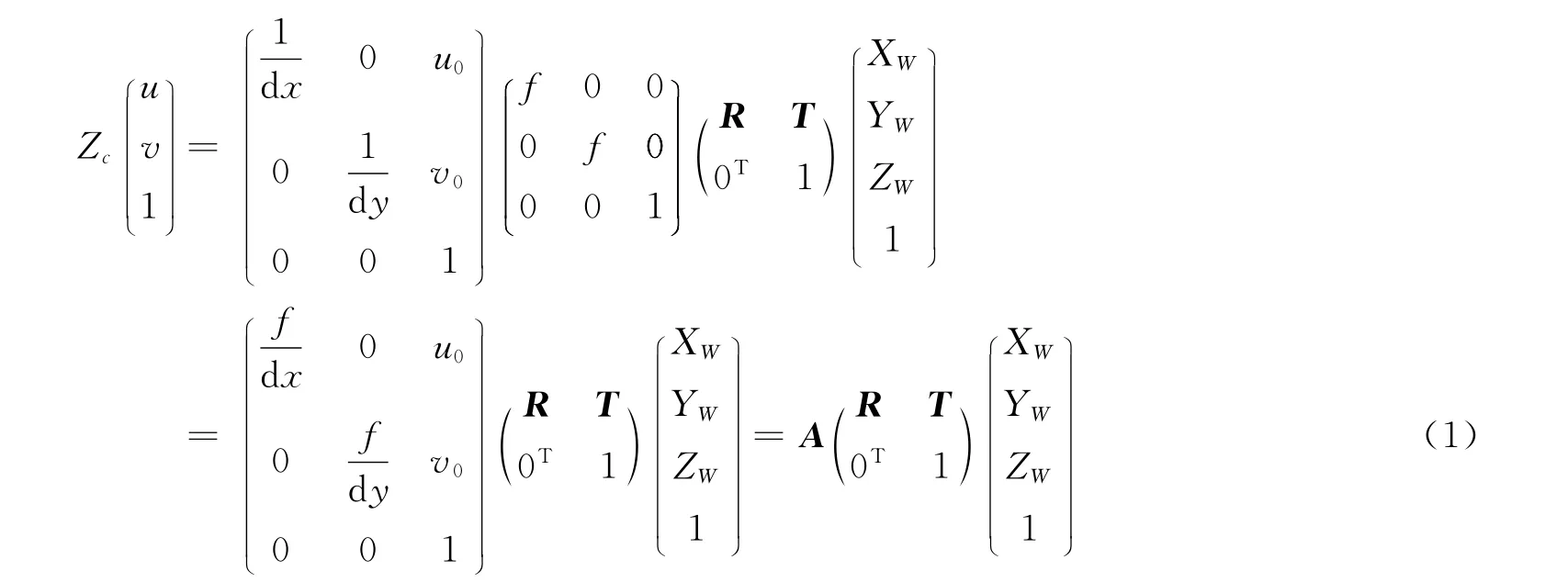
式（1）中，dx×dy是像素點的大小，以mm為單位；0T是零矩陣的轉置矩陣。A只與攝像機內部結構有關，稱其為攝像機內部參數；R，T完全由攝像機相對世界坐標系的方位決定，稱為攝像機的外部參數［5］。

由此可知，若已知攝像機的內外參數A，R，T以及圖像上坐標點的位置（u，v），就可以得到空間坐標點。攝像機標定的過程，就是求解攝像機內外參數的過程。

3.2 參數標定

采用文獻［6］中二維平板的標定法，標定程序的流程圖如圖5所示。

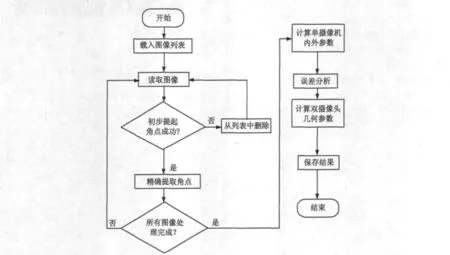
圖5 標定的流程圖Fig.5 The flow chart of calibration

根據平面棋盤格及公式，得出的標定結果如表1所示。

4 圖像處理

將采集得到的原始圖像對進行中值濾波去除孤立圖像噪聲，得到的其中一組圖像對如圖6所示。

濾波后的圖像對在視覺上與原圖像并無差別，所以在對濾波后的圖像進行直方圖均衡化來平衡圖像對之間的亮度差異，可以更清楚直觀地觀察到透鏡與光線的輪廓，直方圖均衡化的圖像對如圖7所示。經過直方圖均衡化后，立體圖像對的亮度差異降低，且亮度明顯提高，較原圖來說可以直觀地看到透鏡與光線的輪廓。

至此，經過圖像預處理的立體圖像對，亮度差異得到改善，灰度均勻地分布在0～255之間，能夠較好地滿足后面立體匹配的要求。

表1 標定結果Tab.1 Result of calibration

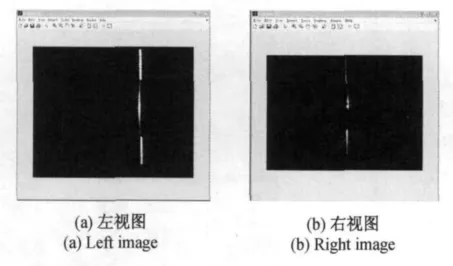
圖6 濾波后的立體圖像對Fig.6 Images from median filter

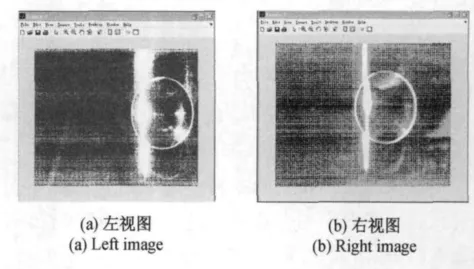
圖7 直方圖均衡后的立體圖像對Fig.7 Images after histogram equalization

4.1 基于區域的立體匹配

基于區域的立體匹配［7－8］就是要衡量像素鄰域（窗口）之間灰度或紋理的相似性。匹配實驗選用像素數為9×9的匹配窗口，以及式（2）所示的最小絕對差算法SAD算子來進行描述，在匹配完成之后需要利用式（3）進行視差圖的校正。

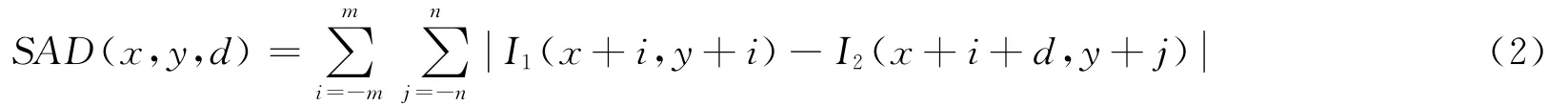
式（2）中，I1為左圖像上任意一點，I2是右圖像上I1的匹配點，d為搜索范圍。

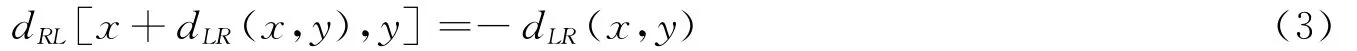
式（3）中，dRL是以左圖為基準，右圖相對于左圖的視差；dLR是以右圖為基準，左圖相對于右圖的視差。

從實驗得到的12組圖片中選擇效果較好的3組圖片進行立體匹配，并采用左右一致性檢驗、中值濾波，二值化等處理，最終輸出視差二值化圖像如圖8所示。

4.2 曲線擬合

立體匹配后的視差二值化圖需要確定其圓環中心點的位置，從3組立體匹配的視差圖中提取多個點，采用最小二乘法來擬合圓與曲線得到圓心坐標及半徑，擬合結果如圖9所示。

圖8 透鏡面形視差圖Fig.8 Parallax image of lens surface characterization

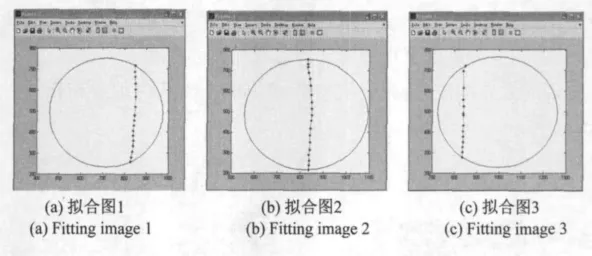
圖9 視差圖擬合Fig.9 Parallax image fitting

現以圖9（c）組擬合圓的圓心和半徑為基準，將圖9（a），圖9（b）擬合圓疊加在圖9（c）擬合圓上，從而構建成設計方案所述的三線激光投影的模型，擬合結果如圖10所示。

4.3 三維重建

在完成的擬合圖中選取多個二維平面坐標點，利用3節介紹的空間點坐標計算方法可得出透鏡表面的空間離散點集。三角剖分采用 Delaunay 標準的 Bowyer－Watson算法來實現［9－10］，剖分圖如圖11所示，并最終在OpenGL中得到透鏡模型的三維立體圖像，如圖12所示。

圖10 三線激光投影擬合圖Fig.10 Fitting image of 3－ray laser projection

圖11 透鏡三角剖分過程圖Fig.11 Lens triangulation process

圖12 透鏡三維重建Fig.12 Lens model 3Dreconstruction

4.4 實驗結果

具體計算重構三維面形的2點PV值，20點PV值和均方根誤差（RMS值），并與單線掃描法檢測的相應結果比較（見表2）。由于單線掃描法檢測光學元件面形的技術目前已經較為成熟，故將三線投影法的檢測結果與之比較即可驗證可行性。

從測量結果比較可以看出，三線投影法與單線掃描法的PV值的差異約為0.02μm，對于RMS值，兩者的差異約為0.03μm，這個結果是較為理想的，與干涉檢測法和數字刀口檢測法的精度是較為接近的，從而驗證了結構光投影法檢測光學元件是可以滿足通常的測量要求，具有一定的可行性。

表2 測量結果比較Tab.2 Comparison of the measurement results

5 結 論

本文采用投影法檢測光學元件面形，即線結構光掃描測量和立體視覺測量相結合的檢測方法，這種方法最終剖分得到的透鏡模型圖像初步具有真實透鏡模型的三維外貌形狀。但由于計算誤差、匹配精度、圖像采集環境等因素的影響，造成最后得到的三維圖像有明顯的變形。為了得到更完善更精細的重建圖像，還需要進一步的研究和改進。

［1］孫國強，許增樸.用于產品造型設計的三維反求測量系統的研究［D］.天津：天津科技大學，2007.

［2］王曉林，陳偉民，黃尚廉.光切法三維輪廓測量的原理及其應用［J］.光學技術，1997，3（2）：39－43.

［3］陳 江.二目立體視覺測量系統關鍵技術研究［D］.南京：南京航空航天大學，2006.

［4］高 文，陳熙霖.計算機視覺—算法與系統原理［M］.北京：清華大學出版社，1999.

［5］宋 龍.線結構光實物反求測量儀的研究與開發［D］.哈爾濱：哈爾濱理工大學，2008.

［6］李洪海，王敬東.攝像機標定技術研究［J］.光學儀器，2007，29（4）：7－11.

［7］達飛鵬，蓋紹彥.光柵投影三維精密測量［M］.北京：科學出版社，2011.

［8］HIRSCHMULLER H.Improvements in real－time correlation－based stereo vision［J］.IEEE Workshop on Stereo and Multi－Baseline Vision，2001，22（11）：141－148.

［9］程曉亮.基于雙目立體視覺的三維重構研究［D］.哈爾濱：哈爾濱工業大學，2006.

［10］WATSON D F.Computing then－dimensional Delaunay tessellation with applications to Voronoi polytopes［J］.The Computer Journal，1981，24（2）：167－172.