BP神經網絡分步賦初值算法的研究
池凱莉,董林璽
(杭州電子科技大學電子信息工程學院,浙江杭州310018)
0 引言
工程中遇到的問題多數是非線性關系,很難用數學模型來計算,而神經網絡具有高度非線性映射的性能特點,只要構建合適的網絡,就可以以任意的精度逼近任何的非線性映射,所以神經網絡有著十分廣泛的應用前景,在網絡監測以及交通、醫療、農業等方面獲得了廣泛的應用。該算法的思想是通過梯度下降法修正各層神經元之間的權值,使誤差不斷下降以達到期望誤差的目的。從本質上說,這種算法是一種迭代過程,迭代算法一般都與初值的選擇密切相關,如果初值選擇不當,則算法的收斂速度會很慢甚至不收斂,在訓練過程中也容易陷入局部極小值。研究者一直致力于算法的改進[1],目前已有很多BP網絡改進算法產生,如:批處理、增加動量項、變學習效率等,然而,這些改進方法都是基于隨機初始化權值進行訓練仿真的,所以不能解決對初始權值的依賴問題。
本研究將采用分步賦值的方法設置初始權值。輸入到最后一級隱層的權值矩陣對網絡的影響不是很大,只要保證網絡的抗干擾性和容錯性,使網絡處于一個很好的狀態即可,本研究采用敏感區賦值,通過矩陣相乘來計算各級的權值。最后一層的輸出權值直接作用于輸出,對算法的影響最大,筆者進行單獨賦值,利用期望值作為實際輸出構成線性方程組,以方程組的解作為輸出層的權矩陣的初始值,這樣不僅可以避免陷入局部最小點,同時也可大大地縮短訓練的時間。
1 BP神經網絡
傳統BP神經網絡的思想是:學習過程由信號的正向傳播與誤差的反向傳播兩個過程組成[2]。正向傳播是將樣本經過逐層處理后傳向輸出層,誤差反傳是將輸出誤差以某種形式通過隱層向輸入層逐層反傳,并將誤差分攤給各層的所有單元,從而獲得各層單元的誤差信號,該信號即作為修正各單元權值的依據。信號正傳后誤差信號反傳,周而復始地進行,該過程就是網絡的學習訓練過程。該過程一直進行到網絡輸出的誤差減少到可以接受的程度,或進行到預先設定的學習次數為止。
筆者以3層的神經網絡為例來闡述神經網絡的工作原理[3],其結構圖如圖1所示。
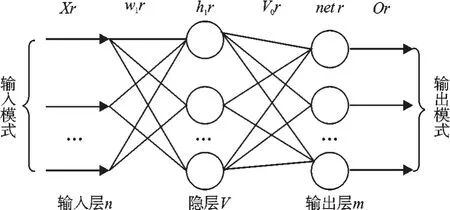
圖13 層BP神經網絡結構
網絡參數如下:輸入樣本數為k,輸入層節點數為n,隱層節點數為v,隱層加權和向量為net,輸出層節點數是m,輸入層到隱層的權值矩陣為Wij,輸出層權值矩陣是Vjk,教師向量是tk,學習效率為η,動量項為ε,輸入和隱層之間的激勵函數是f1,輸出層的激勵函數是函數f2,通常激活函數取單極性S變換函數。
2.1 正向傳播
定義網絡輸出和期望輸出不等時,輸出誤差E可以表示為:

第1隱層加權和netj如下所示:

第1隱層輸出hj如下所示:

第2隱層的加權和與輸出層的輸出計算方法同上。
2.2 反向傳播
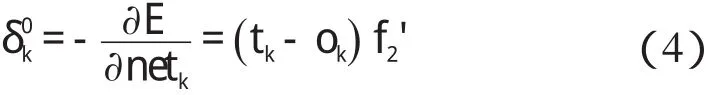
輸出層的權值Δvjk變化如下:
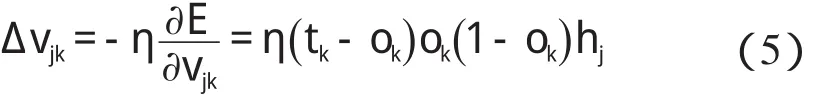
隱層的權值Δwij變化表示為:
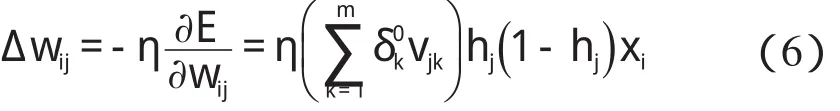
2 BP神經網絡賦初值算法
傳統BP神經網絡算法采用的反向迭代逐步調整各層權值,最終得到最優權值矩陣,研究者利用該矩陣對樣本進行訓練校準,得到更準確的信號數據。但是這種標準的BP算法在應用中暴露了不少內在的缺陷。網絡是在權初值基礎上展開訓練的,因此權值的初值是網絡訓練的最根本的影響因素,有些文獻提出了新的賦初值算法[3-4],主要過程如下。
輸入和隱層之間的激勵函數是線性分段函數f1,輸出層的激勵函數采用的是sigmoid函數f2。其中:p=1,2,3…k。輸入層和隱層、隱層和輸出層的權值矩陣分別是:

輸入層與輸出層的隱層分別采用不同的賦初值方法來賦值,方法如下:首先對輸入層到隱層的權值賦初值,前層對輸出的影響很小,主要考慮的是網絡的抗干擾性,使網絡處于一個良好的狀態,該賦值方法已經被驗證是切實可行的。
為了使前層穩定,最后網絡收斂到設定精度,本研究選擇的激勵函數是已經研究很成熟的單極性的S函數,如下所示:
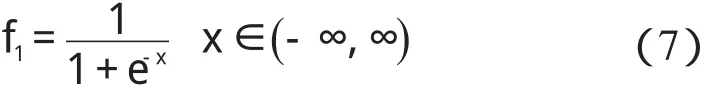
該函數保證隱層的輸出和樣本保持一致的相關性。其賦值原理可總結如下:
f1的反函數如下所示:
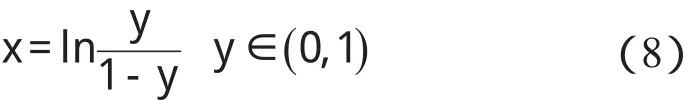
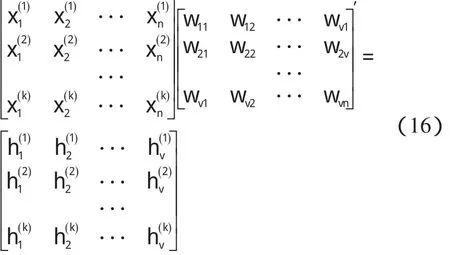
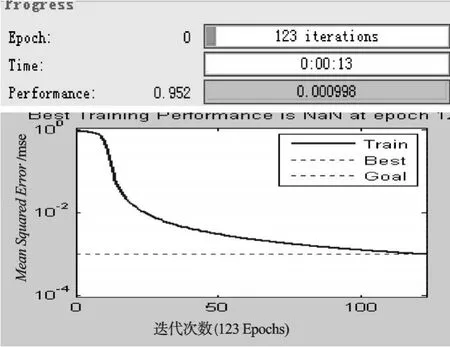
某隱層節點的輸出值是a(-1 一個隱節點的輸出值為a的等值超平面定義為等值超平面Pa,隱層節點的起始節點為P0,具體計算公式如下: 式中:hw—隱層節點權向量w的單位向量,稱為隱層節點方向。 一個隱層節點的a水平敏感區域Aa被本研究定義為節點輸出在(0,a)范圍內輸入區域,敏感區域寬度是由隱層節點的權值和閥值來決定的,從公式(2,3)可以得到a水平敏感區域的寬度Ga可表示為: 本研究采集多組數據,取數據集中的點作為特殊樣本輸入,該樣本是:X=(x1x2x3…xq),其中,q?n。本研究隨機選取兩個不同的樣本點(xh1xh2)作為輸入,如果該兩樣本點對應的輸出相同則重新選擇樣本點。其中前層隱層的賦初值方法可總結如下: (1)激勵函數的敏感區如下: (2)設隱層節點輸出為a(-1 (3)隱層的第i個節點(i (4)重復以上3步選擇不同的樣本值,求出n對權值,這樣就可以求出隱層權值矩陣Wij的初值,Wij=(w1w2…wn)T。 如果不只一個隱層,后面的隱層和輸出的權值矩陣求解可以表示為: 針對后層隱層權值矩陣這樣計算,使得后層的權值矩陣小于前層,保證了網絡的抗干擾性。 這種方法雖然在一定程度上避免了局部極小的問題,但是采集樣本難度大,并且沒有考慮到輸出層的獨特性和重要性。輸出層權值矩陣直接作用于實際輸出,直接決定網絡訓練結果的好壞,所以本研究在前層的賦值基礎上,提出了新的賦初值算法,對輸出層進行單獨的全新賦值。 第1層的權值賦值使用的特殊樣本,由最能反映對象規律的數據組成,緊接其后的采集到的數據應該與前面的數據出入不大,此時對后面的權值賦值和前面的賦值連續,是可行的[5]。在此本研究對輸出層采用新的方法進行求解,為使輸出的數值在一定的范圍內,采集k組樣本Xp=(x1px2px3p…xnp),其中,p 本研究使用的f2也是單極性的S函數,使輸出限制在(0,1)之內,求解線性方程。 其輸出層權值矩陣的賦值步驟可總結如下: (1)求取隱層的輸出hi,激勵函數為f1=x(-1 利用輸出期望值tk,求解f2的反函數得到netq,可以表示為: (2)隱層加權和為netq,求取輸出層第q節點的權值矩陣Vjk,如下所示: 該方程在vk時有解,為了使網絡結果簡單,本研究取v=k方程有唯一解。同時第一隱層采取上述方法賦值的理由是: (1)第一層隱層的矩陣賦值方法可以提高網絡的抗干擾性。在求解輸出層權值矩陣時,前層隱層的輸出h矩陣必須是滿秩,才能保證公式(16)有解。由于第一層權值舉證已經固定,不再變化,本研究多次選擇樣本輸入求解,就可以得到公式(16)的解。 (2)重復上述賦值步驟(1)、(2),輸出層剩下的節點對應的權值也可以得到,解得m個k階方程組即可。通過線性方程組的解和前面得到的輸入到隱層的初值就得到了整個網絡的權值矩陣。 方程的解是輸出層的權矩陣初值,在初值基礎上,通過輸入樣本對網絡進行訓練就可以得到最優的權值矩陣。本研究利用期望輸出來得到初值,十分接近最優權值,通過輸入新的樣本訓練,不僅降低了訓練的時間,也解決了局部極小的問題[6-7]。 本研究采用上述方法對神經網絡進行賦值,輸出層需要求解線性方程組即A X=b,輸入大量不同樣本來求解,然而通常情況下系數矩陣A是不可逆矩陣,所以就不存在根,得不到相應的輸出層的權值矩陣。本研究采用一種Gause-Jardon消元法來解方程組[8],將這個方法解得的輸出層權值矩陣和前層的權值矩陣結合在一起,通過仿真驗證可知其大大地提高了訓練后續樣本的速度,是可行的。以下就簡要地敘述這種消元法的原理。 線性系統A X=b在生產實踐和科學研究中會經常遇到,該矩陣方程的解分為兩種情況:當系數矩陣A的行數大于或者等于列數的時候,方程有解,當行數小于列數的時候,方程無解。 當方程無解的時候,即方陣A沒有可逆矩陣的時候,一般研究者可以在Frobenius范數意義下,找到一時本研究還要借助廣義矩陣[9],來求解此時的逆矩陣。利用廣義矩陣求解的矩陣方程A X=b的極小范數最小二乘解的表達式可所示為: 本研究依據的定理是: 按照該方法就可以求出線性方程A X=b的系數矩陣A的廣義矩陣,繼而可以得到要求的極小范數的最小二乘解。 該實驗構建的是3層2-4-1的神經網絡,訓練算法函數選擇是傳統的梯度最降法,隱層和輸出層的激勵函數是單極性S函數,如公式(7)所示。訓練次數設為30 000,學習效率為0.05,誤差精度為0.001。本研究用傳感器采集溫度數據,選擇樣本集中的點利用敏感區賦值,計算出前層的隱層權值。筆者分別利用兩種不同算法的賦初值的方式,對后續采集的溫度數據進行驗證。 采用文獻[3]中的賦初值算法得到的仿真結果如圖2所示。 圖2 賦初值算法仿真圖 筆者利用本研究提出的分步賦初值算法訓練網絡,得到的仿真圖如圖3所示。 圖3 分步賦初值算法仿真圖 圖2中顯示的是BP賦初值算法的誤差曲線和訓練過程,其誤差曲線平滑緩慢的下降,在訓練了75次誤差接近設定精度的時候,曲線幾乎不再變化,整個訓練過程歷時13 s,平均迭代次數123次。 圖3中顯示的是采用分步賦初值算法訓練的結果,誤差訓練曲線是直線,誤差一直呈直線下降,整個訓練小于1 s,迭代2次。 由上述的分析結果可以看出,優化賦初值算法不僅大大地提高了訓練的速度,而且使誤差函數的下降趨勢變得陡峭,在一定程度上避免了陷入局部極小的現象。 本研究分別利用傳統的BP神經網絡算法和優化的分步賦值算法對樣本進行訓練,可以看出,優化賦值方法使訓練時間縮短到1 s之內,這樣就大大地縮短了數據的處理時間,提高了收斂速度;同時訓練過程沒有出現振蕩,誤差幾乎呈直線下降,克服了傳統BP算法的收斂易陷入局部極小的問題。 計算機仿真結果表明該算法是有效的。 ( ): [1]李良,吳紅娉,陳瑜.基于BP神經網絡算法及推導的研究[J].中國水運,2008,8(1):161-162. [2]韓力群.人工神經網絡教程[M].北京:北京郵電大學出版社,2006. [3]侯媛彬.提高神經網絡收斂速度的一種賦初值算法研究[J].模式識別與人工智能,2001,14(4):385-389. [4]宋紹云,仲濤.BP人工神經網絡的新型算法[J].電腦知識與技術,2009,5(5):1197-1198. [5]陳樺,程云艷.BP神經網絡算法的改進及在Matlab中的實現[J].陜西科技大學學報,2004,22(4):44-47. [6]MENG J E.Face recognition with radial basics function(rbf)neural network[J].IEEE Transactions on Neural Networks,2003,3(3):697-710. [7]張潛,武強.基于BP神經網絡的一種傳感器溫度補償方法[J].電子設計工程,2011,19(9):152-154. [8]SYEDA M,ZHANG Y,PAN Y.Parallel Granular Neural Network forFast Credit Card Fraud Detection[C]//Proceedings of the 2002 IEEE Internatinal Conference on Fuzzy Systerm.2002:572-577. [9]張大志.用Gause-Jardon消去法求解線性方程AX=b的極小范數最小二乘解[J].阜陽師范學院學報,2007,24(3):21-23.
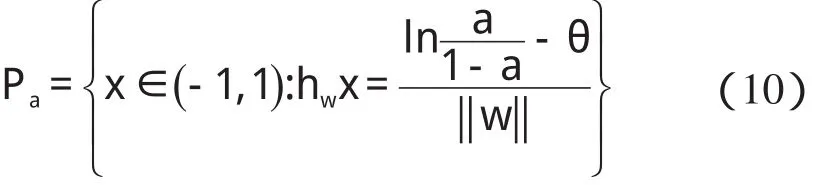

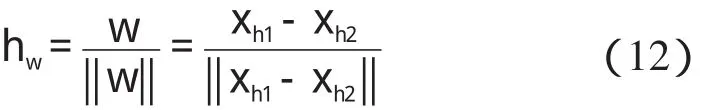
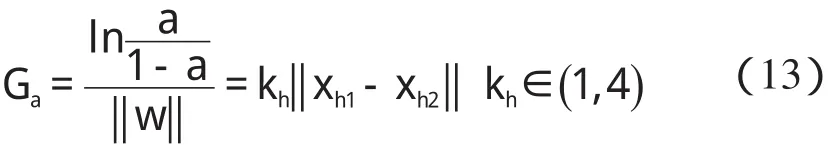
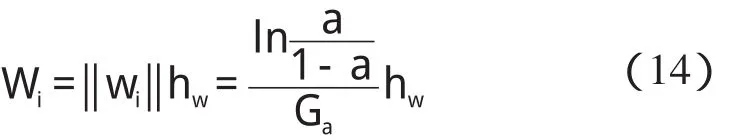
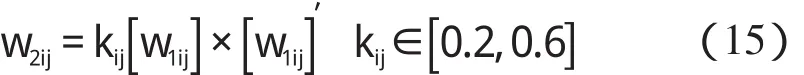
3 BP神經網絡新算法

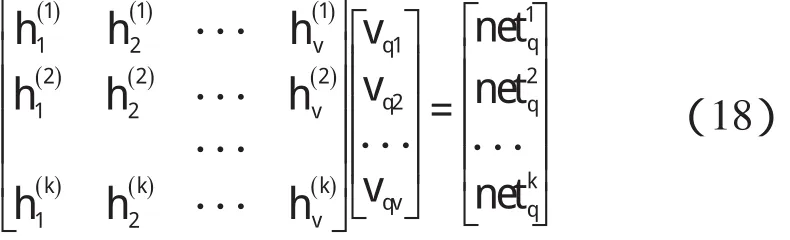

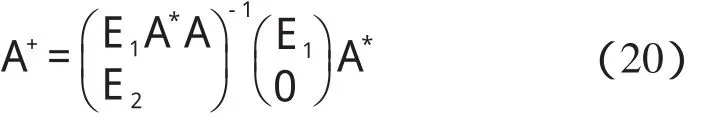
4 Matlab仿真分析與結果

5 結束語

