一種基于反饋的Raptor碼編碼改進方案

張 偉，雷維嘉，謝顯中

(重慶郵電大學移動通信技術重慶市重點實驗室，重慶400065)

0 引言

文獻［1］在1998年首次提出數字噴泉碼這一概念，文獻［2］在2002年給出了第1種實用的數字噴泉碼—LT碼。對于LT碼，編譯碼k個源數據包需要k ln k次異或(XOR)運算，也就是說LT碼并不具有線性時間譯碼［3］。基于此，2006年文獻［4］提出了另外一類數字噴泉碼，即Raptor碼，它由外碼和內碼通過級聯編碼的方式實現。外碼是傳統的信道糾刪碼，內碼是弱化的LT碼。這里，弱化的LT碼是指其度分布中最大度為一個較小的值，且平均度d*是個常數，編譯碼k個源數據包需要kd*次XOR運算。因此，Raptor碼實現了線性時間譯碼。

為了提高噴泉碼的譯碼效率，許多方案都引入了反饋。文獻［5］提出一種實時遺漏糾錯方案，接收端向發送端反饋譯出的源數據包個數，發送端根據反饋信息選擇一個固定的度分布，使接收端譯出全部源數據包的時間減短。同樣，文獻［6］給出一種混合噴泉碼，發送端根據反饋信息直接發送相應的源數據包，加速了譯碼進程。又有學者針對短碼給出一種無率反饋碼方案［7］，該方案通過多次反饋并改變度分布，使譯碼開銷減少等。

以上方案雖然通過反饋提高了譯碼效率，但忽略了譯碼效率變化的特點。本文針對Raptor碼譯碼的最后階段出現譯碼效率明顯降低的問題，提出了一種帶反饋的編碼改進方案，并給出最佳的反饋控制點。仿真結果顯示:改進的方案明顯提高了譯碼效率，減小了譯碼開銷等。

1 Raptor碼

1.1 Raptor碼的編碼和譯碼

Raptor碼的編碼包括預編碼和LT編碼兩部分。預編碼:編碼器對k個源數據包使用糾刪碼(比如，LDPC碼［8］)產生K個中間數據包，其中K比k略大一點。LT編碼:根據弱化的LT碼度分布對K個中間數據包進行噴泉編碼，產生需要的編碼包數量。

相應地，Raptor碼的譯碼包括了兩階段譯碼，采用與LT碼相同的置信傳播算法［2］。LT譯碼:編碼包譯出絕大多數中間數據包。預編碼的譯碼:由譯出的這部分中間數據包恢復全部源數據包。

Mackay在文獻［9］中指出:當譯碼器接收N(N比k略大一點)個編碼包后進行譯碼，有一部分中間數據包不能恢復出來，其比例為f=exp(－d*)。對此，他提出了一種編譯碼策略:預編碼階段應產生k/(1－f)個中間數據包，而譯碼器只需譯出大約k個中間數據包，然后通過預編碼的譯碼恢復全部的源數據包。

1.2 弱化的LT碼度分布

在LT碼的譯碼過程中，為了避免冗余，希望每次迭代中只有一個度為1的編碼包。由此得到一種理想孤子分布ρ:

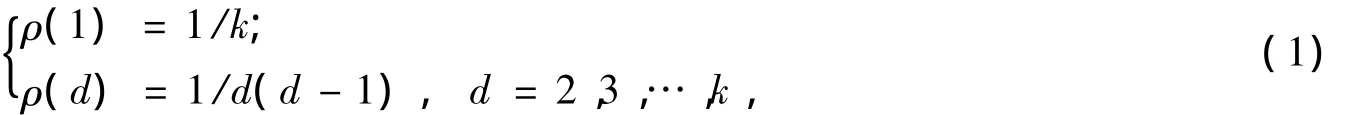
其中，ρ(d)為選到度為d的概率。

然而實際中，理想孤子分布的效果并不好。一方面，譯碼過程中很可能因為沒有度為1的編碼包而出現譯碼中斷;另一方面，編碼時可能有些源數據包沒有被覆蓋，導致無法譯出。Luby對理想孤子分布進行了修改［2］，設計了一個正數函數τ:

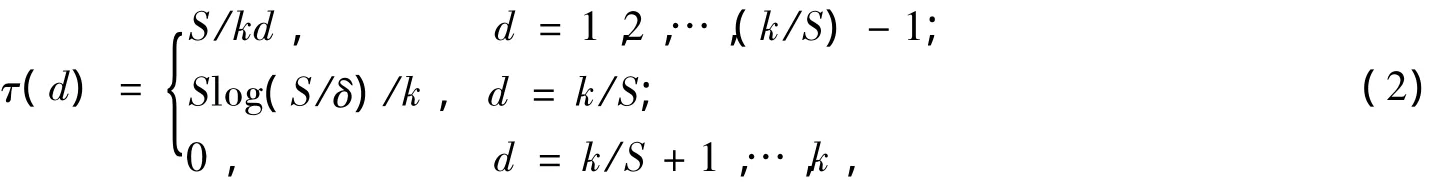
其中，參數с和δ保證了譯碼過程中期望產生度為1的編碼包個數大約為:

式中，с為0和1之間的某一常數;δ為接收一定數量的編碼包后，未能成功譯出全部源數據包的概率。然后，將ρ與τ相加再歸一化得到魯棒孤子分布μ:

魯棒孤子分布的最大度是k，而弱化的LT碼度分布是將魯棒孤子分布的最大度設置成一個較小的值，但理想孤子分布和正數函數的最大度不變［9］，下面定義其表達式:

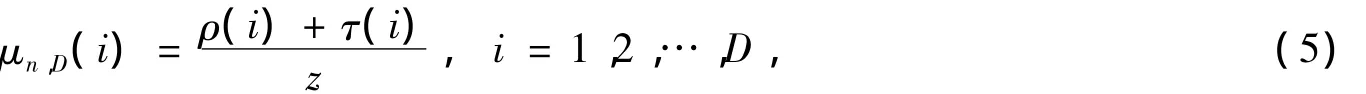
式中，n為參與編碼的數據包個數;D為最大度;i為度;z=ρ(i)+τ(i)。特別地，對于不同的n，當D取8時，μn，D的平均度d*均為3。

2 譯碼性能及改進的編碼方案

2.1 譯碼性能

這里主要研究Raptor碼的LT譯碼階段，即由編碼包譯出k個中間數據包這一過程。預編碼采用LDPC碼，其度分布Ω(x)=(2x+3x2)/5［4］，碼率為0.95。為了便于分析，定義4個參數:譯碼比例β，表示譯出的中間數據包個數M占源數據包個數k的比例，即β=M/k;接收比例θ，表示接收的編碼包個數N占k的比例，即θ=N/k;譯碼效率η=M/N;譯碼開銷ε［10］，表示成功譯碼時接收的編碼包個數與k的差值占k的比例。圖1給出了k分別取1 000和5 000時，多次仿真其譯碼比例β隨接收比例θ變化的曲線，其中每條曲線代表每次仿真的結果。

觀察圖1a中k=1 000的譯碼曲線，當橫坐標0＜θ＜0.8時，曲線比較平緩，縱坐標β的值非常小，只譯出少部分中間數據包，說明譯碼效率很低;當θ大約為0.9時，曲線出現陡增，β迅速增大到0.8左右，表明譯出了大約0.8k個中間數據包，譯碼效率大大提高;最后一段曲線變平緩，β變化緩慢，說明譯碼效率明顯降低，當θ大約為1.2時，譯碼結束，譯碼開銷約為0.2。觀察圖1b，k=5 000時表現出與k=1 000相似的譯碼曲線。

2.2 理論分析

度分布的設計對于數字噴泉碼來說是至關重要的，它的好壞直接決定了譯碼性能。在譯碼過程中，度為1和其他低度的編碼包的數量決定了譯碼能否開始并持續進行，但這些數據包攜帶的原始信息較少，可能不會覆蓋全部的源數據包。為了譯出全部源數據包，譯碼器需要接收更多的編碼包。度分布的平均度代表了平均的編譯碼復雜度。因此，較小的平均度確保了譯碼過程的流暢性，但可能造成譯碼開銷增大。比如，當d*=3，不同k值的譯碼開銷ε均達到了0.2之多，而這個值并不理想。

圖1 不同的源數據包數k，譯碼比例β隨接收比例θ變化的曲線

譯碼開銷增大主要是因為譯碼的最后階段譯碼效率明顯降低。分析認為:當譯碼器譯出大約βk個中間數據包后，編碼器新生成的編碼包中只包含譯出數據包信息的比例為P=βd*，而這些編碼包對未譯出的數據包是冗余信息。由圖1可看出:當β大約為0.8時，曲線開始變平緩。這時，P=0.83，大約為50%。因此，最后階段接收的編碼包中有一半是不包含未譯出的數據包信息，導致了譯碼效率明顯降低。

為了提高這一階段的譯碼效率，編碼器再編碼時可以考慮只對未譯出的數據包進行編碼，但需要譯碼器反饋這部分數據包的包號。下面給出具體的改進方案。

2.3 改進的編碼方案

根據反饋控制編碼器中參與編碼的數據包的思想，改進的編碼方案為:

(Ⅰ)編碼器按照度分布μK，8對K個中間數據包進行噴泉編碼。

(Ⅱ)譯碼器接收一定數量的編碼包后開始譯碼;當譯出大約αk個中間數據包時，向編碼器反饋剩余未譯出的數據包個數(K－αk)和具體數據包的包號。

(Ⅲ)編碼器根據反饋信息，僅對這(K－αk)個數據包按照度分布μ(K－αk)，8噴泉編碼。

(Ⅳ)譯碼器譯出大約k個中間數據包后，由這k個數據包恢復出全部的源數據包。

這里，稱α為反饋控制點。從圖1中曲線的變化趨勢來看，曲線在α=0.8左右開始變平緩，而改進方案的關鍵是α取何值時，可使譯碼開銷最少，即尋找最佳的反饋控制點。從理論上推導最佳的反饋控制點α的值比較困難，本文通過仿真的方法，對不同的源數據包數k、α分別取0.75、0.80、0.85和0.90這4個值，比較各自的譯碼開銷來得到最佳的反饋控制點。圖2仿真了不同的源數據包數k，譯碼開銷ε隨反饋控制點α變化的關系。從該圖可得到最佳的反饋控制點α為0.8，此時譯碼開銷均最少。

改進方案需要譯碼器反饋未譯出數據包的包號，這樣雖然增加了系統的復雜度，但譯碼開銷的大幅降低遠彌補了這一不足。另外，當源數據包數k較大時，反饋數據較多，復雜度增加，也會使總的效率降低。例如k=5 000時，反饋量達到1 000。因此，改進方案更適合k不超過1 000的情況。

3 性能仿真

本文通過仿真的方法，與原來無反饋的編碼方案作比較，驗證改進方案的性能。仿真中，弱化的LT碼度分布中с和δ分別取0.03和0.50。首先，比較兩種方案的譯碼開銷。原來的方案(圖2中，當α= 1.00時縱坐標ε的取值)，對于不同的源數據包k，譯碼開銷都達到了0.22;而改進的方案(圖2中，當α=0.80時縱坐標ε的取值)，譯碼開銷減小了10%左右，且隨著k的增大，譯碼開銷逐漸減小，當k=1 000時，ε僅為0.096。

譯碼效率η是衡量一種方案的性能很重要的參數，η越趨近1說明方案的性能越好。圖3為不同的源數據包數k，兩種方案的譯碼效率對比情況，原來方案的η大約為0.82且隨k的變化很小;改進方案的η隨k的增大而增大，當k=1 000時，η達到了0.91，體現了很好的性能。

為了更清楚表明譯碼的最后階段，改進方案明顯提高了譯碼效率，這里定義另外一個參數，最后階段的譯碼效率η0=0.2k/△N，△N表示譯出最后0.2k個中間數據包，譯碼器還需接收的編碼包數。η0的具體含義為譯碼器接收一個編碼包平均能譯出中間數據包的個數。表1為不同的源數據包數k，兩種方案最后階段的譯碼效率η0對比，由表1可看出:譯碼的最后階段，無反饋的方案中譯碼器接收一個編碼包可譯出一個中間數據包，而改進的方案可譯出兩個中間數據包，效率提高了一倍以上。

圖2 不同的源數據包數k，譯碼開銷ε和反饋控制點α的關系

圖3 不同的源數據包數k，兩種方案的譯碼效率對比情況

4 結束語

本文給出了一種基于反饋的Raptor碼編碼改進方案，它通過反饋來控制編碼器中參與編碼的數據包，減少了冗余信息，提高了最后階段的譯碼效率。經仿真得到最佳的反饋控制點。仿真結果顯示:與原來無反饋的編碼方案比較，改進方案的譯碼性能得到明顯改善。

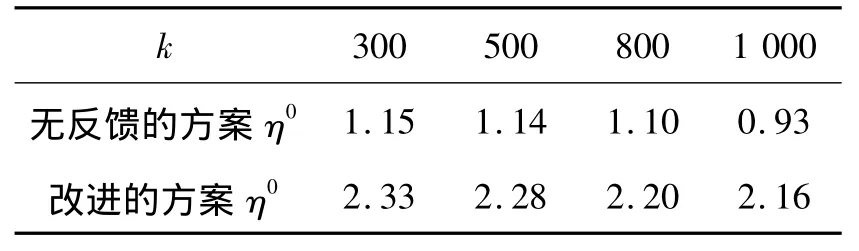
表1 不同的源數據包數k，兩種方案最后階段的譯碼效率η0對比

［1］ Byers J，Luby M，Mitzenmacher M，et al.A Digital Fountain Approach Distribution of Bulk Data［J］.ACM Sigcomm Computer Communication Review，1998，28(4):56－67.

［2］ Luby M.LT Codes［C］//Proceedings of 43rd Annual IEEE Symposium on Foundations of Computer Science(FOCS’02).USA:IEEE Press，2002:271－280.

［3］ 慕建君，焦曉鵬，曹訓志.數字噴泉碼及其應用的研究進展與展望［J］.電子學報，2009，37(7):1571－1577.

［4］ Shokrollahi A.Raptor Codes［J］.IEEE Transactions on Information Theory，2006，52(6):2551－2567.

［5］ Beimel A，Dolev S，Singer N.RTOblivious Erasure Correcting［J］.IEEE/ACM Transactions on Networking，2007，15(6): 1321－1332.

［6］ Kokalj-Filipovic S，Spasojevic P.ARQ with Doped Fountain Decoding［C］//IEEE ISSSTA’08.2008:780－784.

［7］ Jesper H S，Toshiaki K A，Philip O.Rateless Feedback Codes［C］//IEEE International Symposium on Information Theory Proceedings.2012:1767－1771.

［8］ 王立新，劉躍軍，吳亮.基于LDPC優化圖結構的ACE改進算法［J］.河南科技大學學報:自然科學版，2010，31(4):46－52.

［9］ Mackay D JC.Fountain Codes［C］//IEE Communications Proceedings.2005:1062－1068.

［10］ Mitzenmacher M.Digital Fountains:A Survey and Look Forward［C］//IEEE Information Theory Workshop.USA:IEEE Press，2004:271－276.