雙函數(shù)展開法及m KdV方程的行波解

李向正

(河南科技大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，河南洛陽471023)

0 引言

現(xiàn)代物理學(xué)的進(jìn)展在很大程度上為依賴于非線性數(shù)學(xué)及求解非線性方程方法的進(jìn)展［1］。近50年來，利用不同的方法尋求非線性發(fā)展方程的顯式解成為許多研究者的主要目標(biāo)，已經(jīng)構(gòu)造出了很多行之有效的方法，諸如反散射方法、貝克隆變換法、廣田雙線性算子法、截?cái)嗯藖砭S展開法、雙曲正切函數(shù)展開法及其擴(kuò)展、Jacobi橢圓函數(shù)展開法、F展開法［2］、輔助方程法［3－4］、(G'/G)展開法［5］等，然而，至今尚未有一種統(tǒng)一的方法用于處理所有類型的非線性發(fā)展方程。本文提出一種求解非線性發(fā)展方程的雙函數(shù)展開法，在第1部分簡(jiǎn)介該方法，第2部分以mKdV方程為例介紹方法的應(yīng)用，最后給出一些結(jié)論。

1 雙函數(shù)展開法簡(jiǎn)介

給定非線性偏微分方程(PDE)，為簡(jiǎn)單起見以含兩個(gè)自變量為例，

P為其變?cè)亩囗?xiàng)式，其中包含有非線性項(xiàng)和高階偏導(dǎo)數(shù)項(xiàng)。

求方程(1)的行波解

其中，k＞0;ω為待定常數(shù)。將式(2)代入方程(1)，則方程(1)化為u(ξ)的常微分方程(ODE)

設(shè)方程(3)的解u(ξ)可表示為f(ξ)和g(ξ)的多項(xiàng)式

其中，a0，a1，…，an和b1，…，bn是待定常數(shù)，正整數(shù)n由具支配地位的非線性項(xiàng)與最高階偏導(dǎo)數(shù)項(xiàng)的齊次平衡［4－6］確定，f(ξ)和g(ξ)分別為

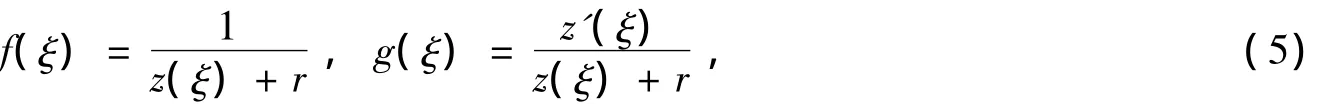
其中，r≥0為待定常數(shù);z(ξ)滿足二階線性O(shè)DE

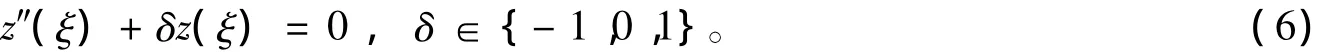
方程(6)的解易于判定并給出。可以解出:

(Ⅰ)當(dāng)δ=－1時(shí)，

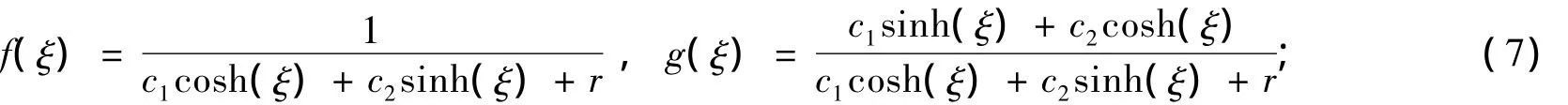
(Ⅱ)當(dāng)δ=0時(shí)，

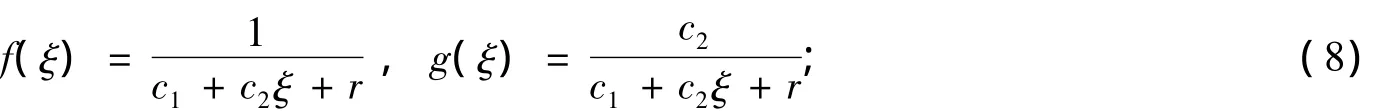
(Ⅲ)當(dāng)δ=1時(shí)，

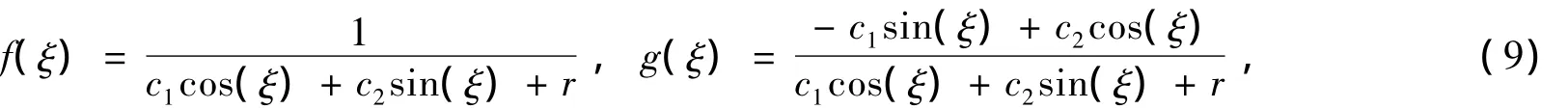
其中，c1、c2為任意常數(shù)。顯然f(ξ)和g(ξ)滿足如下關(guān)系

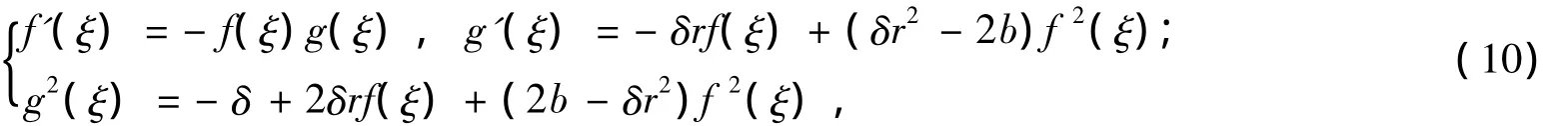
其中，z'2(ξ)=2b－δz2(ξ)，b為積分常數(shù)，且b≠δr2/2。

將式(4)代入方程(3)，利用式(10)可將方程(3)的左端變成f(ξ)和g(ξ)的多項(xiàng)式。置f(ξ)和g(ξ)的各次冪項(xiàng)的系數(shù)為零，得到包含所有待定常數(shù)的非線性代數(shù)方程組。解上述代數(shù)方程組(可借助Mathematica或Maple)，將結(jié)果代入式(4)得PDE(1)的行波解。

2 m KdV方程的行波解

考慮如下形式的mKdV方程

其中，β＞0是實(shí)常數(shù)。尋找方程(11)的行波解

其中，k＞0;ω為待定常數(shù)。

利用行波約化式(12)，方程(11)轉(zhuǎn)化為u=u(ξ)的ODE

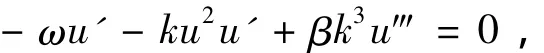
關(guān)于ξ積分一次得

其中，C是待定積分常數(shù)。

考慮方程(13)中u″和u3的齊次平衡(n+2=3n?n=1)，可設(shè)方程(19)的解具有形式

其中，a0、a1、b1是待定常數(shù)。

將式(14)代入方程(13)，利用方程(10)，合并f(ξ)和g(ξ)的同類項(xiàng)，方程(13)的左側(cè)可以轉(zhuǎn)化為f(ξ)和g(ξ)的多項(xiàng)式(其中若出現(xiàn)g2(ξ)項(xiàng)，則可利用關(guān)系式(10)將其轉(zhuǎn)化為f(ξ)的多項(xiàng)式)。令多項(xiàng)式的系數(shù)為零，得到一組關(guān)于a0，a1，b1，k，ω和r的代數(shù)方程組，解此代數(shù)方程組，可得到7種類型的解:

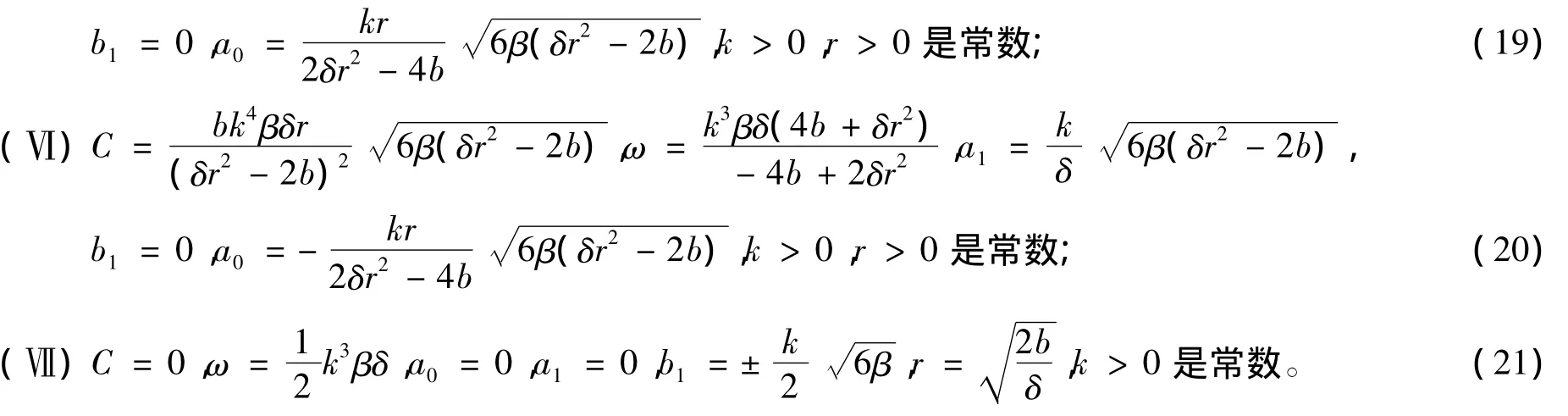
將解(15)～(21)分別代入方程(14)，可得到mKdV方程(11)的精確行波解。

(ⅰ)將解(15)代入方程(14)可得mKdV方程(11)的3種類型的行波解。

其中c1和c2為任意常數(shù)(下同)。

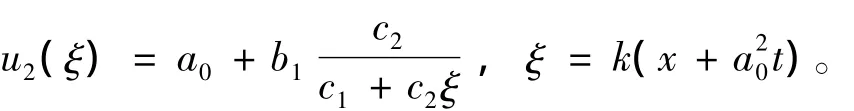
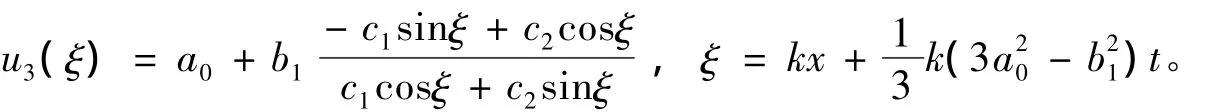
(ⅱ)將解(16)代入方程(14)可得mKdV方程(11)的3種類型的行波解。

當(dāng)δ=－1，C=0時(shí)，

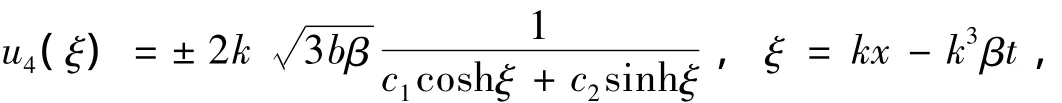
其中，b≥0為任意常數(shù)。

當(dāng)δ=0，C=0時(shí)，

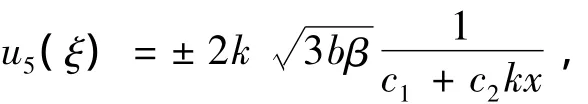
其中，b≥0為任意常數(shù)。

當(dāng)δ=1，C=0時(shí)，

其中，b≥0為任意常數(shù)。

(ⅲ)將解(17)代入方程(14)可得mKdV方程(11)的3種類型的行波解。

當(dāng)δ=－1，C=0時(shí)，

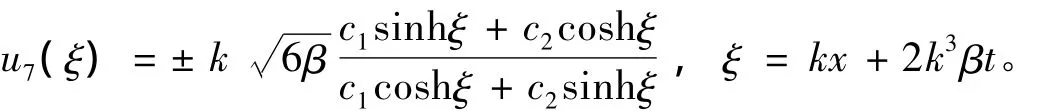
當(dāng)δ=0，C=0時(shí)，

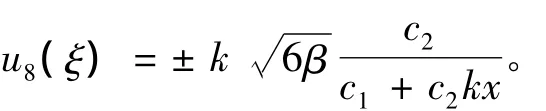
當(dāng)δ=1，C=0時(shí)，

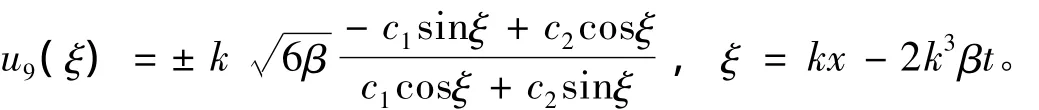
(ⅳ)將解(18)代入方程(14)可得mKdV方程(11)的3種類型的行波解。

當(dāng)δ=－1，C=0時(shí)，

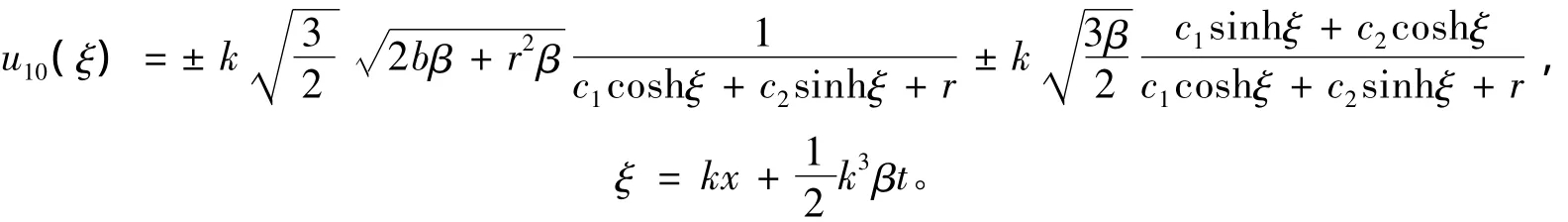
當(dāng)δ=0，C=0時(shí)，

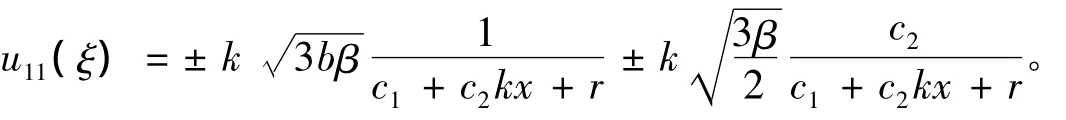
當(dāng)δ=1，C=0時(shí)，

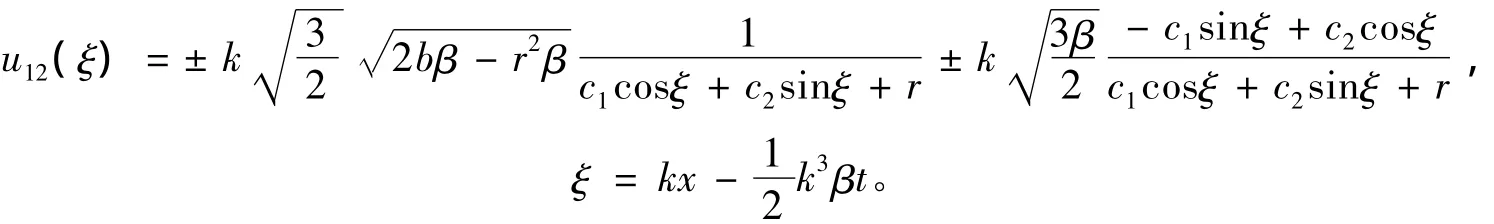
(ⅴ)將解(19)代入方程(14)可得mKdV方程(11)的2種類型的行波解。

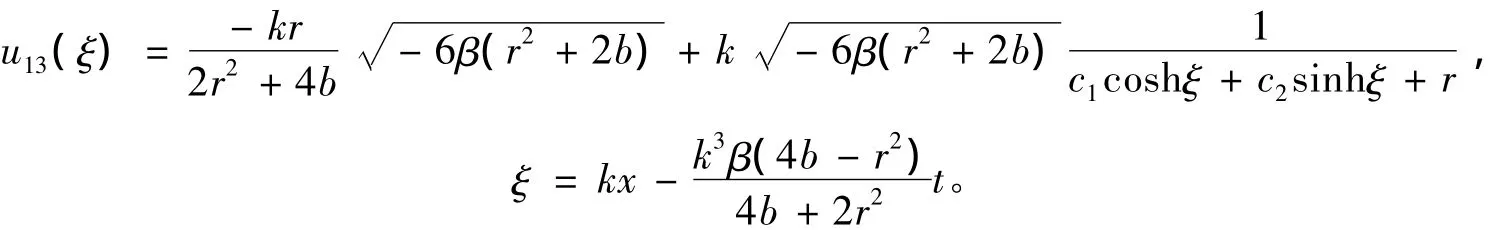
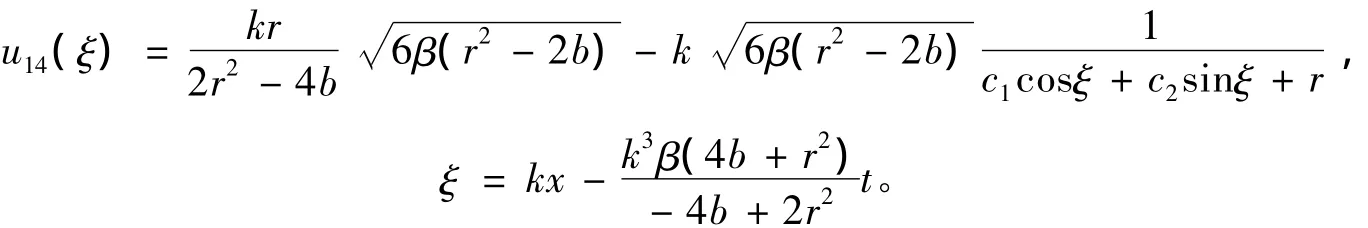
(ⅵ)將解(20)代入方程(14)可得mKdV方程(11)的2種類型的行波解。

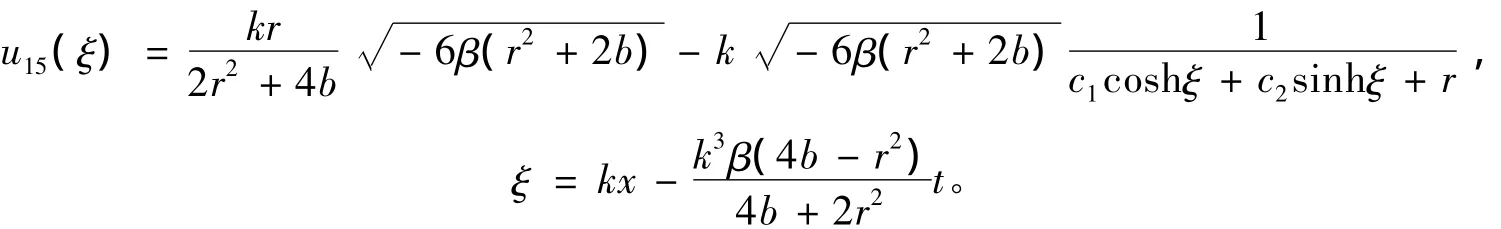
(ⅶ)將解(21)代入方程(14)可得mKdV方程(11)的2種類型的行波解。

當(dāng)δ=－1，C=0時(shí)，

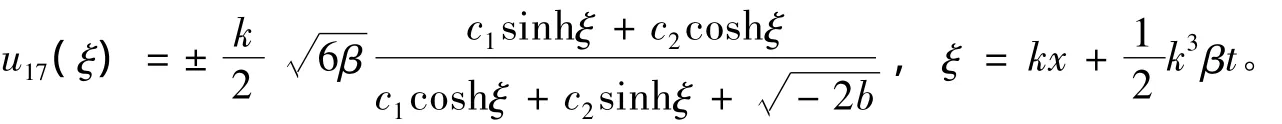
當(dāng)δ=1，C=0時(shí)，

3 結(jié)論

本文利用雙函數(shù)展開法求出了mKdV方程的許多行波解，其中，u1～u3，u10～u18為文獻(xiàn)［5，7］中沒有出現(xiàn)的新解。首先，該方法的要點(diǎn)在于假設(shè)行波約化所得ODE的解可表示為f(ξ)和g(ξ)的多項(xiàng)式，多項(xiàng)式的階數(shù)可由齊次平衡得到，多項(xiàng)式的系數(shù)可通過求解相關(guān)的代數(shù)方程組得到。函數(shù)f(ξ)，g(ξ)由函數(shù)z(ξ)表示，z(ξ)滿足一個(gè)二階線性O(shè)DE。第二，解所得代數(shù)方程組非常重要，一般可借助于Mathematica或Maple軟件解出，然而對(duì)于復(fù)雜的非線性演化方程組，其解未必能解出，但雙函數(shù)展開法依然十分重要。第三，雙函數(shù)展開法直接、簡(jiǎn)潔、基本和有效，其中二階線性O(shè)DE的解眾所周知。本方法還可用于求解Klein-Gordon方程［8］，KdV方程［9］，KdV-Burgers方程［10］，KP方程［11］等，將陸續(xù)報(bào)告相關(guān)結(jié)果。

［1］ Joel S.Shock Waves and Reaction-diffusion Equations［M］.New York:Springer-Verlag New York Inc，1983.

［2］ 李向正，張金良，王躍明，等.非線性Schrodinger方程的包絡(luò)波解［J］.物理學(xué)報(bào)，2004，53(12):4045－4051.

［3］ Sirendaoreji S J.Auxiliary Equation Method for Solving Nonlinear Differential Equations［J］.Phys Lett A，2003，309:387－396.

［4］ Li X Z，Wang M L.A Sub-ODEMethod for Finding Exact Solutions of a Generalized KdV-mKdV Equation with High-order Nonlinear Terms［J］.Physics Letters A，2007，361:115－118.

［5］ Wang M L，Li X Z，Zhang J L.The(G’/G)-expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics［J］.Physics Letters A，2008，372(4):417－423.

［6］ Wang M L.Solitary Wave Solutions for Variant Boussinesq Equations［J］.Physics Letters A，1995，199:169－172.

［7］ 李修勇，秦青，李保安，等.mKdV方程的精確解［J］.河南科技大學(xué)學(xué)報(bào):自然科學(xué)版，2004，25(4):86－89.

［8］ Qin Y P.Exact Solutions to the Klein-Gordon Equation in the Vicinity of Schwarzschild Black Holes［J］.Science China，2012，55(3):381－384.

［9］ 李向正，李修勇.F展開法的發(fā)展和兩個(gè)廣義KdV方程的孤立波解［J］.河南科技大學(xué)學(xué)報(bào):自然科學(xué)版，2006，27 (5):90－92.

［10］ 李向正，王躍明，李曉燕，等.組合KdV-Burgers方程的一種解法［J］.河南科技大學(xué)學(xué)報(bào):自然科學(xué)版，2003，24 (4):104－107.

［11］ Wang Y Y，Zhang JF.Variable Coefficient KPEquation and Solitonic Solution for Two-temperature Ions in Dusty Plasma［J］.Physics Letters A，2006，352:155－162.