BD-2/GPS組合導(dǎo)航系統(tǒng)選星算法及定位分析

應(yīng)士君， 李金金， 劉衛(wèi)， 邱烺

(上海海事大學(xué) 商船學(xué)院，上海 201306)

0 引 言

隨著衛(wèi)星導(dǎo)航系統(tǒng)在各個領(lǐng)域中的應(yīng)用，人們對衛(wèi)星定位技術(shù)的要求越來越高，而定位精度是判斷衛(wèi)星定位效果好壞的最主要標(biāo)準(zhǔn).[1]目前，世界上投入實際運行的全球定位系統(tǒng)只有美國的GPS和俄羅斯的GLONASS，還有正在建設(shè)中的中國北斗二代(BD-2)衛(wèi)星導(dǎo)航定位系統(tǒng)和歐洲的伽利略系統(tǒng).北斗衛(wèi)星導(dǎo)航系統(tǒng)(BeiDou(COMPASS)Navigation Satellite System)是我國正在實施的自主發(fā)展、獨立運行的全球衛(wèi)星導(dǎo)航系統(tǒng)，是具有民族意義的研發(fā)項目.2012年9月19日，第14和15顆北斗導(dǎo)航衛(wèi)星被成功送入預(yù)定轉(zhuǎn)移軌道.

多系統(tǒng)組合定位[2]具有可見衛(wèi)星數(shù)(Visible Satellite Number,VSN)多、定位精度高等優(yōu)點，所以多系統(tǒng)組合的研究顯得尤為重要.由于多系統(tǒng)組合增加VSN，如何快速、準(zhǔn)確地選擇定位衛(wèi)星在整個導(dǎo)航定位過程中起著至關(guān)重要的作用，本文主要介紹BD-2/GPS組合導(dǎo)航系統(tǒng)[3]的選星算法.目前的選星算法主要有傳統(tǒng)選星算法、基于衛(wèi)星幾何精度因子(GDOP)貢獻法[4]、基于仰角和方位角法[5]及模糊選星算法等，BD-2/GPS組合導(dǎo)航系統(tǒng)VSN增加，傳統(tǒng)的選星算法計算量大，不能達到快速定位[6]的要求.本文提出一種基于遺傳算法的定位選星算法，將各組衛(wèi)星中最優(yōu)GDOP作為算法尋優(yōu)的目標(biāo)函數(shù)，選出最佳定位衛(wèi)星組合，最后通過48 h實地觀測數(shù)據(jù)對比分析最佳GDOP算法和本文所提選星算法的定位精度，最終驗證該算法的可行性及優(yōu)越性.

1 組合系統(tǒng)GDOP算法改進

衛(wèi)星導(dǎo)航在一定的偽距測量誤差下，一般利用GDOP表征定位精度的大小，反映由于衛(wèi)星幾何布局的影響所造成的偽距測量誤差與定位誤差間的比例系數(shù)，是對偽距測量誤差的放大倍數(shù).定位衛(wèi)星選擇的基本原則就是選取GDOP最小的衛(wèi)星組合，使可選衛(wèi)星組合的定位精度達到最大.[7]由于利用BD-2/GPS組合系統(tǒng)定位增加鐘差變量，所以至少需要5顆衛(wèi)星實現(xiàn)定位、定時計算.GDOP(式中用λGDOP代替)計算過程如下：

(2)

式中:l,m,n表示方向余弦;N表示用于解算的衛(wèi)星個數(shù).觀測矩陣為

(3)

則幾何誤差系數(shù)可以表示為

(4)

式中:t代表矩陣求跡運算.從式(4)可見，每計算一次λGDOP就要進行一次矩陣乘和矩陣逆運算，組合系統(tǒng)VSN的增加使運算量加大，系統(tǒng)實時性較差.因此，可化簡式(4)，避免矩陣乘和矩陣逆運算[8].

簡化式(4)可得：

(5)

經(jīng)化簡，λGDOP可表示為

(6)

式中:aij表示觀測矩陣的伴隨矩陣元[9].

2 BD-2/GPS組合導(dǎo)航系統(tǒng)的選星算法

選星在導(dǎo)航定位中起著至關(guān)重要的作用，選擇最佳幾何構(gòu)成的星座可以達到高精度的定位要求，因此需要合適的選星算法完成快速、準(zhǔn)確的星座組合[10].遺傳算法模擬自然選擇和自然遺傳過程中發(fā)生的繁殖、交叉和基因突變現(xiàn)象，在每次迭代中都保留一組候選解，并按某種指標(biāo)從解群中選取較優(yōu)的個體，利用遺傳算子(選擇、交叉和變異)對這些個體進行組合，產(chǎn)生新一代的候選解群，重復(fù)此過程，直到滿足某種收斂指標(biāo)為止.[11]基于遺傳算法比傳統(tǒng)優(yōu)化算法應(yīng)用范圍廣、全局優(yōu)化性好、魯棒性和通用性強、隱含并行性高、易于實現(xiàn)等優(yōu)勢，本文提出一種基于遺傳算法的選星算法[12].

同時，由于GDOP是影響衛(wèi)星定位精度的主要因素之一，GDOP的大小代表定位精度的高低，GDOP越小，定位精度越高，故以GDOP計算模型作為遺傳算法中判斷解優(yōu)劣的適應(yīng)度函數(shù).

由衛(wèi)星對地面目標(biāo)和地球的覆蓋特性可知，頂座星仰角越大GDOP越小，底座星仰角越小GDOP越小，所以最佳星座組合中必然包括仰角最大和最小的那兩顆衛(wèi)星.將GPS導(dǎo)航衛(wèi)星從0到23分別編號，北斗導(dǎo)航衛(wèi)星從24到38分別編號.BD-2/GPS組合導(dǎo)航系統(tǒng)在高度角大于5°時，平均捕獲跟蹤12顆衛(wèi)星，從中選擇仰角最大的衛(wèi)星(假設(shè)為6號衛(wèi)星，則字符串編碼為000110)；25號衛(wèi)星編碼為011001，然后從剩下的11顆衛(wèi)星中任意選取4顆衛(wèi)星進行組合.假設(shè)選取的樣本為1號、15號、23號、30號、32號衛(wèi)星，則染色體編碼為000001 001111 010111 011110 100000.經(jīng)過交叉變異，適應(yīng)度較高的部分樣本遺傳到下一代，再進行交叉變異，最終達到最優(yōu)解，選擇最佳幾何構(gòu)成的星座組合.選星算法流程見圖1.

圖1 選星算法流程

以上工作全部由軟件完成，通過軟件計算最終得到GDOP最小的組合衛(wèi)星編號.

3 BD-2/GPS組合導(dǎo)航系統(tǒng)實驗結(jié)果分析

導(dǎo)航接收天線安裝在上海海事大學(xué)商船學(xué)院C樓樓頂，位置為：30°52′26.927″N，121°54′7.974″E.接收機參數(shù)設(shè)置如下.

定位參數(shù)設(shè)置：信噪比門限值為36 dB/Hz，高度角為5°，PDOP(空間位置精度因子)門限值為36，RAIM(接收機自主完好性監(jiān)控)門限值為80.

接收機基帶工作參數(shù)設(shè)置：多普勒頻率搜索區(qū)間為-10～10，500 Hz，環(huán)路積累時間為4 ms，環(huán)路類型為3PLL，鎖相環(huán)帶寬為18 Hz，鎖頻環(huán)帶寬為5 Hz.數(shù)據(jù)分析結(jié)果如下.

3.1 VSN

圖2，3和表1為48 h內(nèi)接收機同時工作在兩種不同定位模式下的VSN示意圖.

圖2 BD-2/GPS導(dǎo)航系統(tǒng)VSN

通過以上數(shù)據(jù)可以明顯看出，組合導(dǎo)航系統(tǒng)在相同條件下能夠捕獲的衛(wèi)星數(shù)目遠大于單一系統(tǒng).

圖3 GPS導(dǎo)航系統(tǒng)VSN

表1各系統(tǒng)VSN顆

導(dǎo)航系統(tǒng)最多最少平均BD?2/GPS16512GPS1348

組合導(dǎo)航系統(tǒng)可以選擇最合適的星座組合，達到高精度定位要求，特別是在惡劣環(huán)境下，也可以有足夠數(shù)目的衛(wèi)星進行星座組合，達到定位要求.

3.2 某一采樣時段內(nèi)可見衛(wèi)星的原始數(shù)據(jù)

此時段內(nèi)捕獲跟蹤到16顆衛(wèi)星，GPS導(dǎo)航衛(wèi)星9顆，北斗導(dǎo)航衛(wèi)星7顆，衛(wèi)星分布均勻，為選擇最佳星座組合提供足夠的衛(wèi)星.可見衛(wèi)星的原始數(shù)據(jù)見表2.

表2 可見衛(wèi)星的原始數(shù)據(jù)

通過表2可以看出:仰角最大的衛(wèi)星是GPS的11號星，本文設(shè)置編號為10;仰角最小的衛(wèi)星是GPS的13號星，本文設(shè)置編號為12.所以，最佳衛(wèi)星星座組合必然包括GPS的11和13號星.

矩陣乘法和矩陣求逆運算比較復(fù)雜，在計算機上實現(xiàn)占用資源相當(dāng)多[13]；而利用本文提出的方法，首先將GDOP計算過程簡化，避免大量矩陣運算，然后通過仰角選出2顆定位衛(wèi)星，最后通過遺傳算法選擇最終定位衛(wèi)星組成.某一采樣時段內(nèi)最佳GDOP算法與本文提出算法的分析結(jié)果見表3.

表3 某一采樣時段內(nèi)的分析結(jié)果

48 h內(nèi)最佳GDOP算法與本文提出選星算法的λGDOP及差值對比見圖4～6.

圖4 本文提出選星算法的λGDOP

圖5 最佳GDOP算法的λGDOP

圖6 本文提出選星算法與最佳GDOP算法的λGDOP差值變化曲線

通過表3和圖4～6可見：本文提出選星算法得出的λGDOP和最佳GDOP法得到的λGDOP的誤差值很小，48 h內(nèi)輸出172 696個數(shù)據(jù)的λGDOP差值平均為0.063 042 945，最大誤差為3.1，最小誤差為0.在部分時間段內(nèi)出現(xiàn)較大差值，是由于遺傳算法尋優(yōu)過程出現(xiàn)局部最優(yōu)解.在遺傳算法中，交叉和變異算子發(fā)生的頻率分別由交叉概率和變異概率控制；在迭代過程中，由于隨機誤差使得全局最優(yōu)解有可能丟失，所以需要設(shè)置適當(dāng)?shù)慕徊娓怕手岛妥儺惛怕手?對于出現(xiàn)局部最優(yōu)情況，可以通過以下幾種方法解決：根據(jù)個體適應(yīng)度值，自適應(yīng)地調(diào)節(jié)交叉概率和變異概率；群體有陷入局部最優(yōu)解的趨勢時，相應(yīng)提高交叉概率和變異概率；群體在解空間發(fā)散時，降低交叉概率和變異概率；也可以使用模擬退火算法或神經(jīng)網(wǎng)絡(luò)[14]方法進行改進.

數(shù)據(jù)設(shè)置每秒更新1次，最佳GDOP算法與本文提出算法在20 min內(nèi)所用時間對比見圖7和8.

圖7 最佳GDOP算法所用時間變化曲線

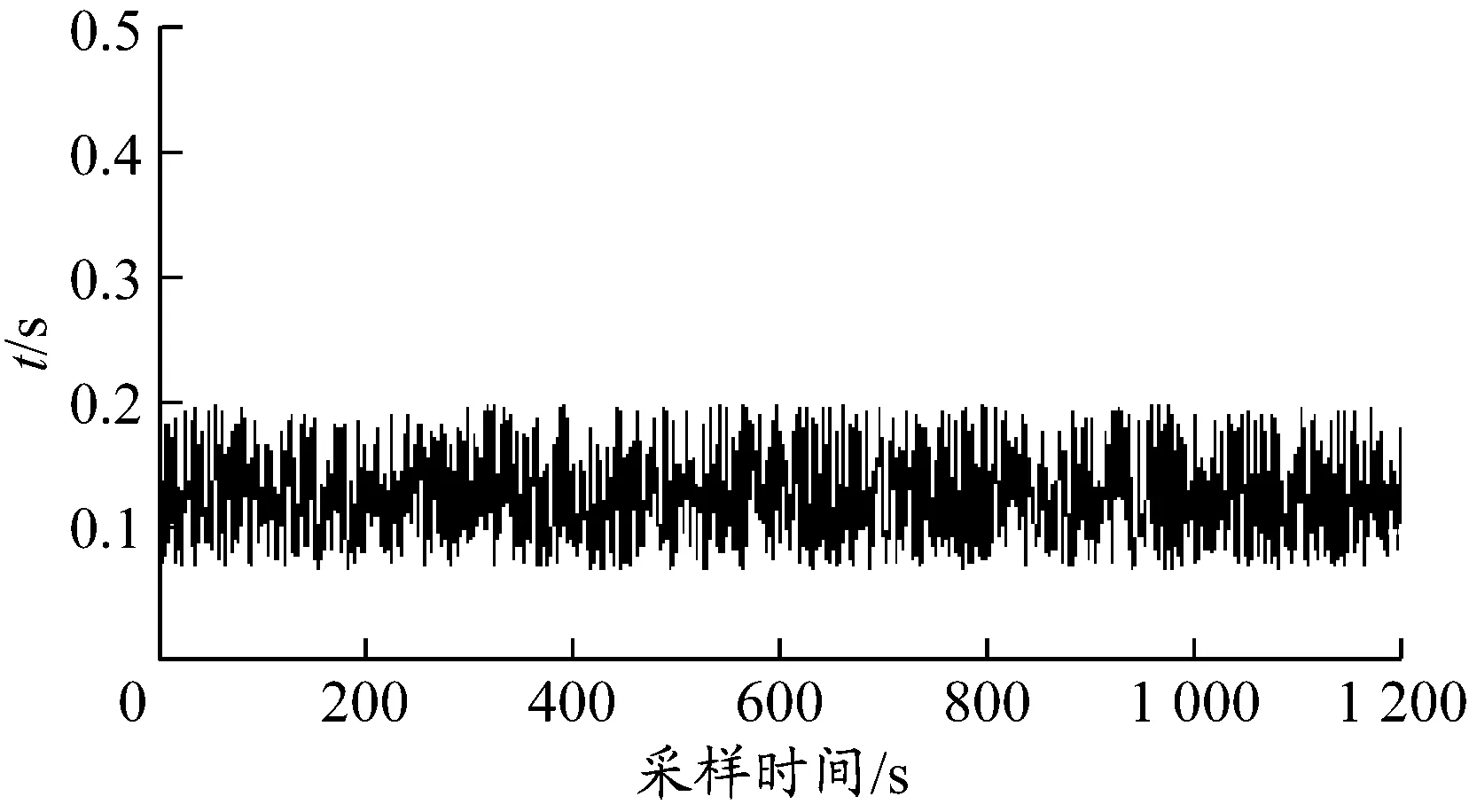
圖8 本文提出算法所用時間變化曲線

4 結(jié)束語

將可見衛(wèi)星仰角與遺傳算法相結(jié)合，以GDOP計算模型作為遺傳算法中判斷解優(yōu)劣的適應(yīng)度函數(shù)，提出一種新的組合導(dǎo)航系統(tǒng)選星算法.算法同時將GDOP計算過程簡化，結(jié)合遺傳算法尋優(yōu)的特點實現(xiàn)最優(yōu)定位衛(wèi)星組合的快速求解，在達到定位精

度要求的前提下有效節(jié)省算法的執(zhí)行時間，效率大大提高.實驗數(shù)據(jù)分析結(jié)果驗證算法的可行性、準(zhǔn)確性和快速性.

參考文獻：

[1] 孫洪瑞, 沈云中, 周澤波. GPS/GLONASS組合點定位模型及其精度分析[J]. 測繪工程, 2009, 18(1): 8-10.

[2] 龐春雷, 趙修斌, 盧艷娥, 等. BD-2/GPS雙模導(dǎo)航定位精度分析及仿真[J]. 現(xiàn)代防御技術(shù), 2011, 39(4): 35-54.

[3] 孫延鵬, 張贏碩, 王爾申, 等. BD-2/GPS組合系統(tǒng)的設(shè)計與定位算法[J]. 電子設(shè)計工程, 2011, 19(23): 74-77.

[4] 叢麗, 談?wù)怪? 提高衛(wèi)星導(dǎo)航定位精度和實時性的選星算法[J]. 系統(tǒng)工程與電子技術(shù), 2008， 30(10): 1914-1917.

[5] 吳瑞祥, 蔡體菁. 基于高度角和方位角的選星方法[J]. 艦船電子工程, 2009, 185(11): 73-75.

[6] 高迪駒. 基于北斗衛(wèi)星通信系統(tǒng)的船載終端串口通信[J]. 上海海事大學(xué)學(xué)報, 2008, 29(4): 10-14.

[7] HURSKAINEN H. Research tools and architectural considerations for future GNSS receivers[D]. Tampere, Finland: Tarnpere Univ of Technol, 2009.

[8] MA Rui, MA Yingli. Study on positioning algorithm for the combined Galileo/GPS system[J]. J Telemetry Tracking & Command, 2009, 30(1): 7-11.

[9] 黃繼拯, 劉紅, 趙艷, 等. GPS/北斗的組合選星算法研究[J]. 艦船電子工程, 2011, 32(8): 81-83.

[10] 金玲, 黃智剛, 李銳, 等. 多衛(wèi)星組合系統(tǒng)的快速選星算法研究[J]. 電子學(xué)報, 2009, 37(9): 1931-1936.

[11] 白治江, 劉廣鐘. 遞歸式多目標(biāo)遺傳算法[J]. 上海海事大學(xué)學(xué)報, 2007, 28(2): 62-74.

[12] 張尚悅, 賈傳熒. 基于遺傳算法的最佳天文定位星座組合[J]. 交通運輸工程學(xué)報, 2004, 4(1): 110-113.

[13] 應(yīng)士君, 王坤, 劉衛(wèi), 等. 基于北斗二代系統(tǒng)的船載定位終端[J]. 上海海事大學(xué)學(xué)報, 2012, 33(3): 1-4.

[14] 朱武亭, 劉以建. BP網(wǎng)絡(luò)應(yīng)用中的問題及其解決[J]. 上海海事大學(xué)學(xué)報, 2005, 26(2): 64-66.