環境激勵下大跨度連續剛構橋動力分析模型修正

盧海林，吳 玏，黃民水，徐文勝

(1．武漢工程大學環境與城市建設學院，湖北 武漢 430074； 2．華中科技大學土木工程與力學學院，湖北 武漢430074)

0 引 言

傳統橋梁安全性評估主要依據表觀損傷調查的結果.隨著檢測技術和計算機技術的發展，對于大型橋梁結構進行損傷識別，都通過建立有限元模型進行仿真分析[1].但是，按照橋梁設計圖建立的有限元模型往往不能完全反映橋梁結構的真實狀態，這就需要對有限元模型進行修正.本文采用基于優化理論的模型修正法修正大型橋梁結構動力分析模型.該方法在不影響橋梁正常使用的情況下，通過環境激勵下橋梁的振動測試，采用功率譜峰值法來獲得大型橋梁主要模態特征值，然后挑選對于模態數據有足夠靈敏度的參數進行修正.參數型模型修正計算復雜，具有非線性特點，修正后的有限元動力分析模型可以更高精度的反映橋梁結構的真實狀態.

通過該方法修正的動力分析模型用于橋梁結構損傷識別可以提高損傷量的判斷和損傷的定位的精度.本文應用該方法對黃河某特大橋的有限元動力分析模型進行了修正.

1 模態識別

傳統模態識別方法，為了建立頻響函數必須同時知道系統的輸入-輸出，然而對大型橋梁結構，人工激勵復雜昂貴，且效果并不理想.基于環境激勵的模態識別方法克服了這些缺點，直接利用行人、風、地面微動等環境作用下，橋梁所受的激勵是平穩的各態歷經寬帶隨機力，其響應的主諧量是在其固有頻率附近的振動，然后獲得結構各階頻率.

環境激勵模態參數識別方法主要有峰值法(PP)、頻域分解法(FDD)、NExT-ERA法、隨機減量法(RD-ITD)、時間序列分析法(AR/ARMA)、隨機子空間法(SSI)[2]等.功率譜峰值法在工程上廣泛應用.其原理為假設輸入為平穩白噪音激勵時，環境振動響應的自功率譜函數和頻響函數具有相似關系[3]，如式(1).

Syy(ω)=H(ω)RuuHH(ω)

(1)

Syy(ω)為自功率譜函數，H(ω)為頻響函數，Ruu為常數矩陣.如果結構阻尼比較小，模態頻率近似平均分布，則在固有頻率ωi處，可以將功率譜模態近似分解式為：

(2)

理論上，系統的各階頻率都應該可以在功率譜圖中找到對應的峰值點.選取峰值點，就可以確定結構的頻率.根據動力響應信號的功率譜密度曲線進行參數識別，快速準確，是橋梁檢測中最常用的方法之一.但也存在峰值選取具有主觀性的特點，因此需要檢測人員具有相應的工程實際經驗[4].

2 參數化模型修正

2.1 參數化有限元模型

考慮后期要通過ANSYS的優化功能進行參數化選代修正，前期有限元模型(FE)建立須考慮以下幾個問題：

a.參數化模型建立.對于大型橋梁建模，利用ANSYS的GUI界面繁瑣復雜，且不利于進行后期參數化迭代計算，所以使用APDL語言(ANSYS Parametric Design Language,參量化設計語言)建立模型幾乎成了唯一的選擇.

b.采用BEAM188單元.BEAM188單元適合分析從細長到中等粗短的梁結構，該單元基于鐵木辛哥梁結構理論，并考慮了剪切變形.SECTYPE,SECDATA, SECWRITE,SECREAD, SECOFFSET等命令可以將自定義的梁截面寫入，并調整截面中原始參考點，生成變截面梁；利用 *do,i,,命令可以進行大量循環創建常截面和變截面梁單元.同時，相對于Solid45單元建模后迭代計算費時太長，BEAM188單元計算耗時相對較少，適合大型工程實際應用.

c.建立較為完善的邊界條件，選用適當的物理參數，對不同強度混凝土采用不同的彈性模量和密度.

2.2 參數型模型修正

模型修正是伴隨有限元理論發展而發展起來的，它利用振動測試得到的動力特性來修正理論模型，使得修正后理論模型的模態參數與實測參數接近.類型大致可以分為：參數型模型修正，矩陣型模型修正[4].

參數型修正法則是對矩陣元素或結構的設計參數(如材料的E，ρ，A，I等)進行修正.這種方法物理意義明確，實用性強，能保持系統矩陣的對稱帶狀特征，便于實際大型橋梁分析計算，并與其它結構優化設計過程密切相關.其主要缺點是計算復雜，對非線性目標函數的優化采用迭代算法，其修正效果也依賴于計算方法和測試精度，而且難以引入振型修正[5].

參數型修正方法又可以分為模態法與頻響函數法，本文采用模態法，其思路與結構優化理論類似，基本原理如下[6]：

無阻尼結構動力方程為:

MA{x″}+KA{x}={0}

(3)

MA、KA為系統質量和剛度矩陣.理論頻率和振型分別為ωA、ΦA，它們與實際結構的動力學特性，即通過實驗模態分析分別獲得的頻率ωt和振型Φt，有一定的誤差.兩者之間差值為：

ΔΦ=Φt-ΦA

(4)

Δω=ωτ-ωA

(5)

引入參數ε，則實測值和理論值的關系可以表達為：

ωt=ωA+εΔω

(6)

Φr=ΦA+εΔΦ

(7)

設Mt、Kt具有ε的冪次級數形式：

Mt=MA+εΔM1+ε2ΔM2+L

(8)

Kt=KA+εΔK1+ε2ΔK2+L

(9)

由振型歸一化正交性條件有：

(10)

KtΦt=MtΦtωt

(11)

對質量矩陣進行修正，將(5)、(6)代入(8)，可得

(ΦA+εΔΦ)T(MA+εM1+…)(ΦA+εΦ)=I

(12)

展開式(10)，收集同次冪的項，得

(13)

(14)

……

由式(12)得到

(15)

式中ΔΦ、ΦA和MA為已知，可以得到M的修正量ΔM.然后對K進行修正，現將式 (5)、(6)、(7)代入式(9)得：

(KA+εΔK1+…)(ΦA+εΔΦ)=

(MA+εΔM1+…)(ΦA+εΔΦ)(εA+εΔω)

(16)

展開式(14)，收集同次冪的項，得

KAΦA=MAΦAωA

(17)

式(15)是原方程的特征方程.

KAΔΦ+ΔK1ΦA=MAΦAΔω+ΔM1ΦAωA+MAΔΦωA

(18)

由式(16)得到:

ΔK1ΦA=MAΦAΔω+ΔM1ΦAωA+MAΔΦωA-KAΔΦ

(19)

ΔΦ、Δω都是已知的，若ΔM=0，可以得到K的修正量ΔK[7].

3 工程實例

3.1 有限元模型建立與模態分析

黃河某特大橋(圖1)起點樁號K598+882.600，終點樁號K599+702.750，橋梁全長為820.15 m.孔跨布置為40+88+2×160+88(連續剛構)+7×40(m)(先簡支后連續T梁)，橋共分4聯.兩側各設50 cm防撞護欄，預制梁頂設6 cm混凝土調平層，FYT-1型防水材料、10 cm瀝青混凝土橋面鋪裝，主橋下部橋墩為鋼筋混凝土雙肢薄壁變截面矩形空心墩，墩高86～100 m，墩頂雙壁中距10 m.

圖1 黃河某特大橋Fig.1 Grand bridge in the Huang River

a.主橋結構布置：88+2×160+88 m(連續剛構)預應力混凝土箱梁.

b.橋面寬度：10.0+2×0.5 m(防撞護欄).

c.道路等級：公路-Ⅰ級.

d.設計車速：60 km/h.

本文采用BEAM188，link2(模擬預應力鋼筋)單元，采用參數化方法建立仿真模型；主梁混凝土采用C50，橋墩混凝土采用C40，預應力鋼筋采用fpk=1 860 MPa鋼絞線.對有限元模型(圖2)進行模態分析，結果如表1所示.

圖2 有限元模型Fig.2 Finite element model

3.2 振動測試

測試系統采用DH3817N，傳感器有4個(如圖3)，分別為DH610V(1個)，地震所941B型傳感器(1個，V08358)，DH610H(2個)，3個測點，每個測點1-2號傳感器測豎向加速度，3號測橫橋向加速度，4號測縱橋向加速度.在第3、5跨選擇3/4截面、1/2截面和1/4截面作為控制截面，每截面選擇一個測點，該測點沿豎向布置兩個拾振器，橋縱向和橋橫向各布置一個拾振器.將拾振器布置在各測點，采用脈動法測試橋梁結構的脈動位移曲線，如圖4.進行功率譜分析后得到橋梁結構的自振特性.圖4中峰值都代表可能的固有頻率，但還必須排除由于車輛隨機制動力和豎向>沖擊力造成的功率譜波段雜亂，所以要與ANSYS模型分析的頻率進行比對和排查.理論值與實測值結果見表2.

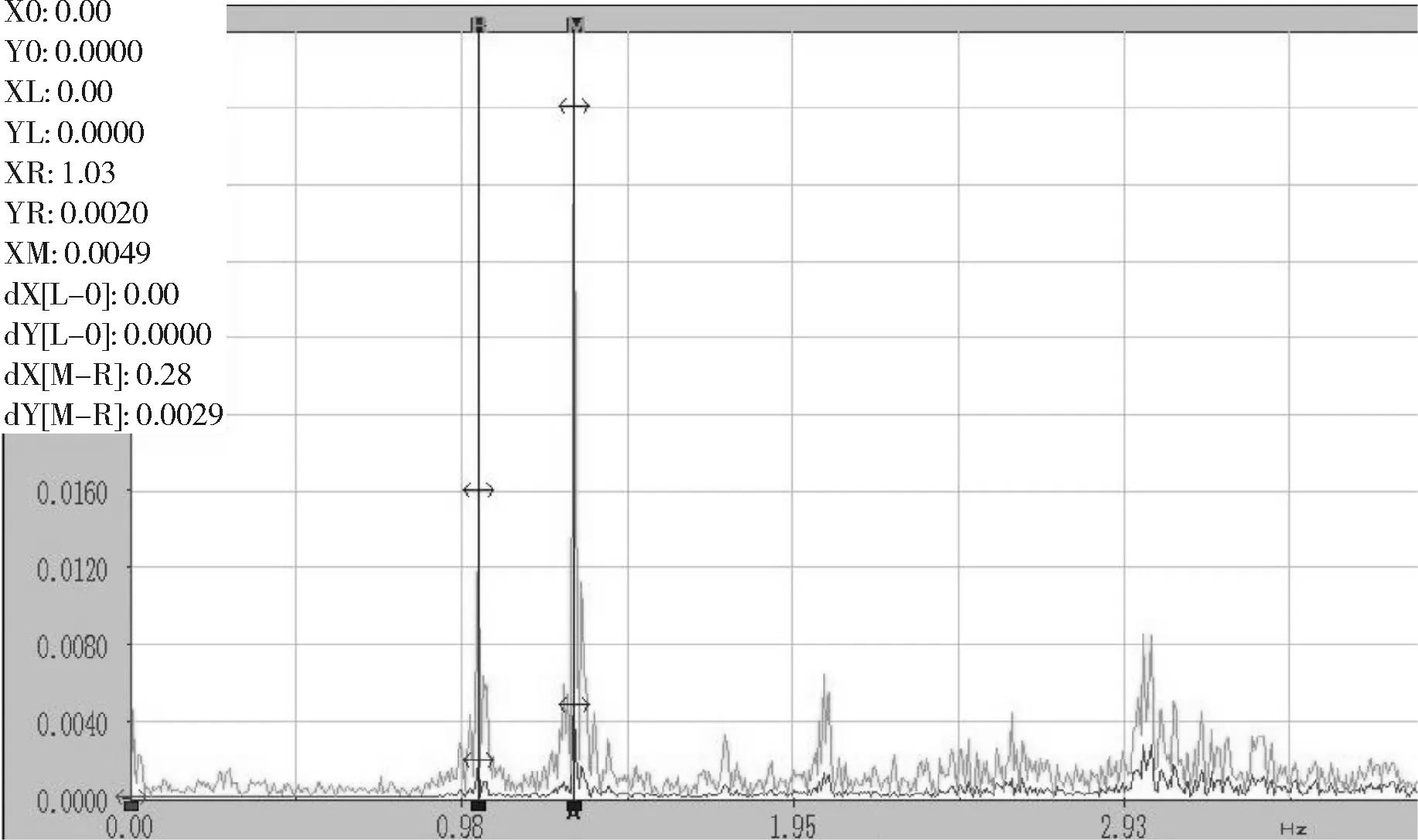
圖4 功率譜峰值法Fig.4 Method of power spectrum peak

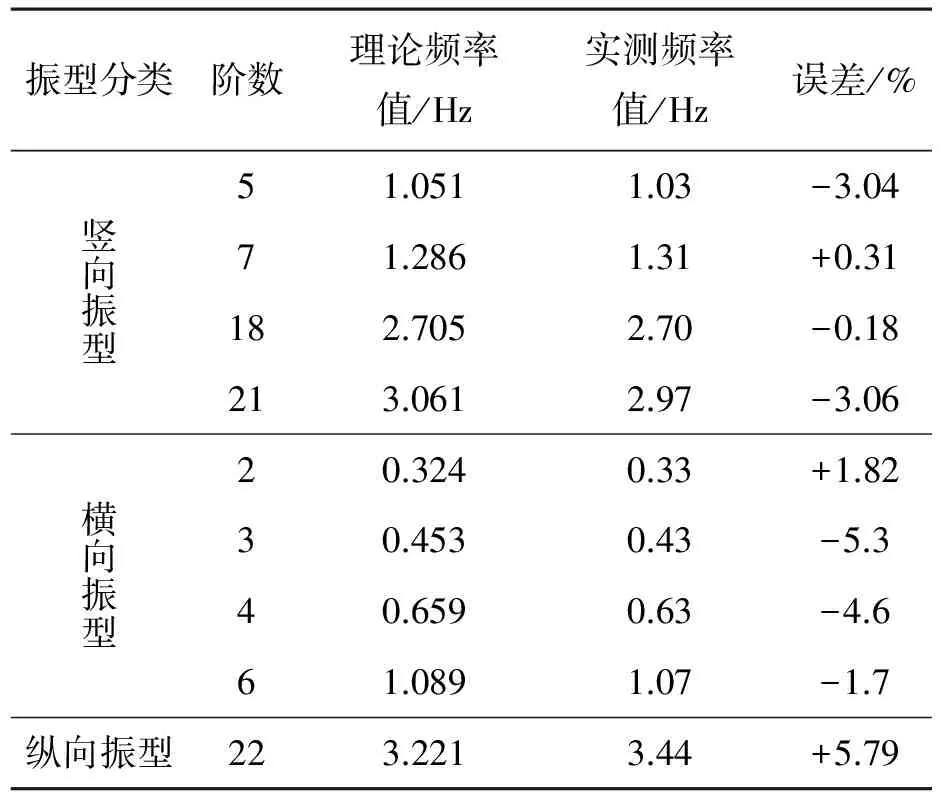
表2 理論值與實測值Table 2 Theoretical values and measured values

3.3 修正參數

ANSYS可以利用PSD命令從主要參數(包括主梁高度h1,頂板厚度T1,底板厚度T2,主梁彈性模量E1、高墩彈性模量E2、箱梁混凝土密度ρ1)中選取模態參數靈敏度高的值.研究中發現，相對于各階頻率，主梁的混凝土彈性模量變化最為明顯.假設主梁初始彈性模量設計值為3.55×1010，當混凝土彈性模量提高15%，豎向基頻增加約28.8%，橫向基頻增加約48.5%，縱向基頻增加約5.4%，即豎向頻率與橫向頻率對彈性模量變化比較敏感，而縱向頻率對主梁彈性模量的變化反應不明顯，并且在后續損傷識別過程中，通過表征剛度的參數來判別損傷是常用手段之一.根據結構動力學原理，剛度元素中包含表達式EI或EA，都與彈性模量有直接的關系，所以，本文選擇彈性模量EI為主要修正參數.

利用ANSYS的APDL語言，將第三跨1號單元到22號單元劃分為四段，1到2號單元彈性模量設置為EX1，3到9號單元彈性模量設置為EX2，10到16號單元彈性模量設置為EX3，17到22號單元彈性模量設置為EX4.同理，根據對稱性，第六跨可以布置為四段，分別為EX22，EX23，EX24，EX25.三個0號箱分別設置為EX5，EX13，EX21，第四跨分別為EX6，EX7，EX8，EX9，EX10，EX11，EX12，第五跨分別為EX14，EX15，EX16，EX17，EX18，EX19，EX20.劃分原則是將跨中部位箱梁的頂板和底板尺寸變化不大者，劃分為同一彈性模量段，將梁高、頂底板厚度按照二次曲線變化劃分為三段.這樣，就將橋梁彈性模量劃分為25個區段，保證修正后能初步判斷箱梁剛度下降段位置.

初次計算時，賦予EX1～EX25=3.55×1010，運用： opvar，EXi，DV，0，4.0e10，1e4將EX1至EX25定為設計變量，其上限為4.0×1010，下限為0，步長為1.0×104；也可以將下限值適當提高，適當縮小搜索范圍，降低收斂運算次數.

將理論頻率和實測頻率之間相對誤差的平方和定義為目標函數，分別提取表2中的兩組值，得到公式(20)和(21).

(20)

(21)

再以橋梁結構在環境激勵下的動力響應作為約束條件和目標函數，在一定范圍內搜索設計變量的取值.尋求f(x)最小值的過程，就是不斷調整目標函數，從而使主梁彈性模量不斷向實際值逼近的過程.利用ANSYS命令：*get，freqi，mode，i，freq 來提取需要模態的頻率，然后使用ANSYS命令：opvar，f(x) ，obj，，，1e-4 來實現目標函數的最小化.其中步長為1×10-4[8].

4.4 修正結果

ANSYS通過循環30次，其中第8次迭代為最優解，最終結果如表3.

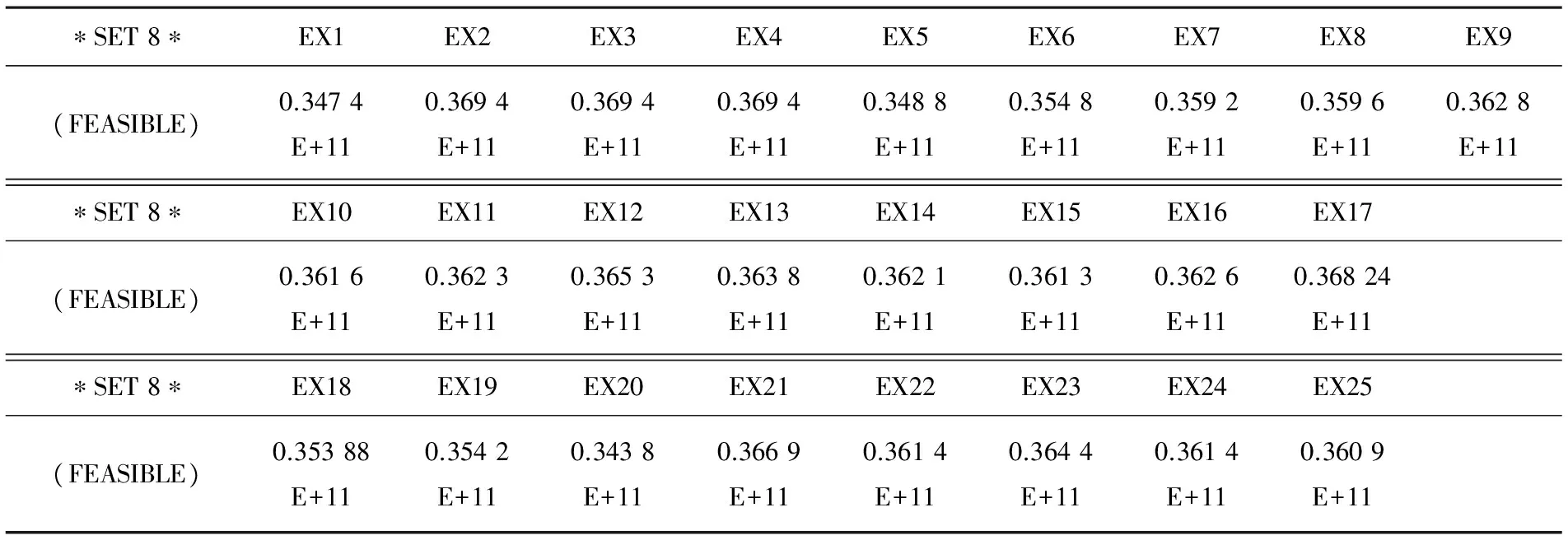
表3 迭代后彈性模量值Table 3 The elastic modulus value after iteration

通過迭代修正后，頻率與修正前頻率對比如表4所示.

從修正后的模型可以快速判斷橋梁健康狀況，也可為后續的損傷識別提供依據.

a.總體動力特性良好；修正后除個別梁段外，彈性模量均高于規范值，反映出橋梁總體滿足承載能力的設計要求.

b.預應力混凝土構件由于全截面(無裂縫)或接近全截面(裂縫控制)參與工作，所以其結構剛度本應該比普通混凝土構件大[9]，但從修正結果可以看出，局部梁段混凝土彈性模量比規范值略低，分別集中在：第三跨懸臂梁端部、第四跨左側根部、第五跨右側根部，如圖5所示.圖中顏色深度表示彈性模量下降的程度.分析其原因主要有以下幾點.

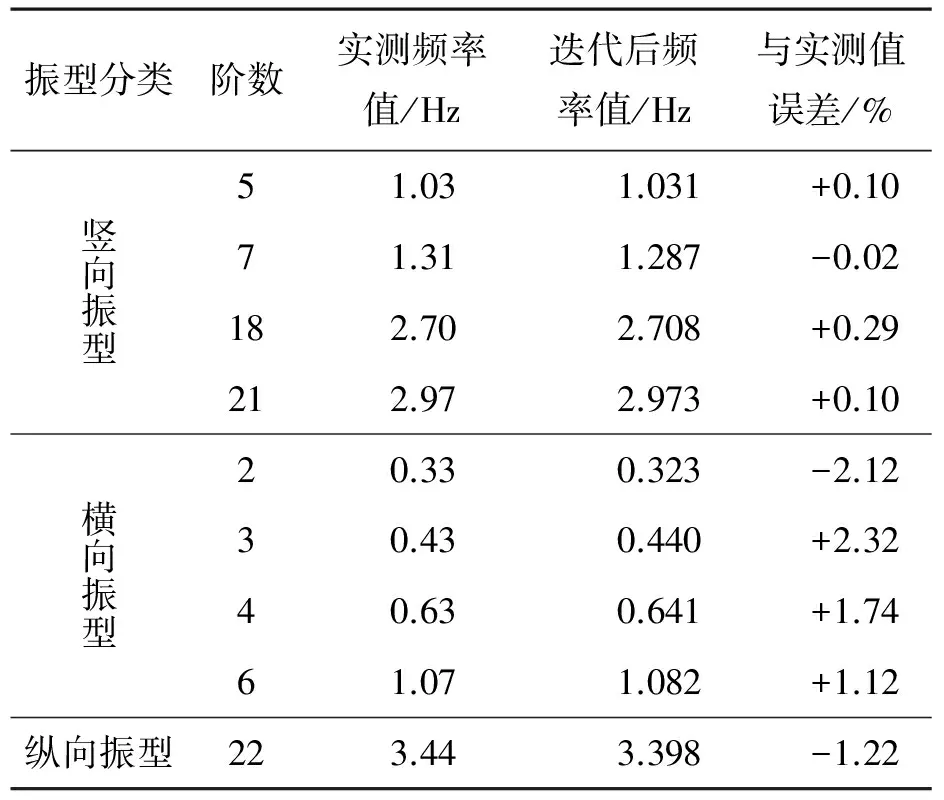
表4 迭代后模型頻率與實測值對比Table 4 After iteration model frequency compared with the measured values

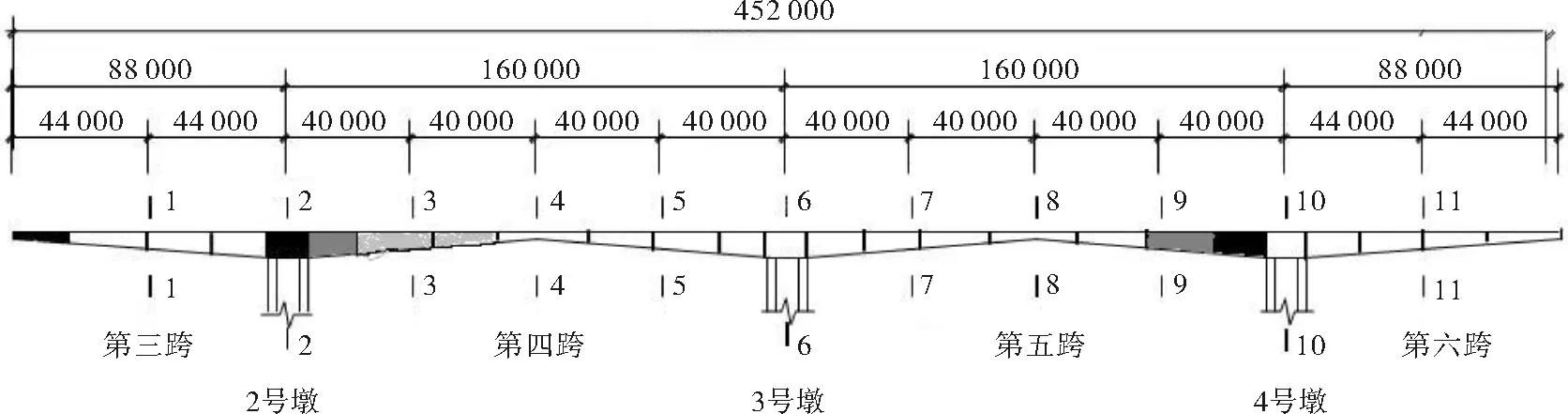
圖5 梁段彈性模量Fig.5 Elasticity modulus of beam sections

①現場觀察，大型運煤車隊通過該橋頻繁來往于附近煤礦，車隊超載較為嚴重.主梁根部負彎矩和剪力較大.同時超載也可能使主梁跨中撓度超過限定值，進一步增大梁根部彎矩[10].

②混凝土澆筑質量問題.箱梁內部表面可見蜂窩和裸露鋼筋，可能是混凝土澆模時，保護層墊塊移位或混凝土漏振、振搗不均勻造成的.

③第三跨懸臂梁處彈性模量下降可能由于引橋部分橋墩不均勻沉降、支座側斜或轉動不自如等造成的，原因需要進一步調查.

④混凝土的彈性模量本身具有一定的離散性，這可能也是修正后的彈性模量與規范值有偏差的原因之一.

4 結 語

a.有限元模型的修正使模型的動力特性與實際情況更加接近，各階頻率修正后的誤差基本在2%以下，精度較高.

b.本文所采用的基于優化理論的有限元動力模型修正方法，利用現有的有限元軟件ANSYS，不用再次輸出繁瑣的M、K和C矩陣即可進行有限元模型修正，快速有效，適合于大型橋梁工程實際應用.

c.經過有限元模型修正，理論模態值與實測模態值基本吻合，可以作為橋梁健康監測和損傷識別的依據，也可為后續橋梁預防性養護等工作提供理論指導.

致謝

本研究得到湖北省教育廳和武漢工程大學的經費資助，在此一并表示衷心地感謝！

參考文獻：

[1] 王元清，姚南，張天申，等.基于最優化理論的多階段模型修正及其在橋梁安全評估中的應用[J].工程力學，2010,27(1):91-97.

WANG Yuan-qing,YAO Nan,ZHANG Tian-shen,et al. An application of multistage model updating based on optimization theory to the safety appraisal of bridge[J], Engineering Mechanics, 2010,27(1):91-97.(in Chinese)

[2] 陳宇．有限元模型修正技術在橋梁工程中的應用研究[D]. 成都：西南交通大學,2009.

CHEN Yu.Research on the Applic-ation of Finite Element Model Updating Technique in Bridge Engineering[D].Chengdu:Southwest Jiao-tong University,2009.(in Chinese)

[3] 劉繼承，周傳榮.一個基于優化的有限元模型修正方法[J].振動與沖擊，2010，22(2):330-340.

Liu Jicheng,Zhou Chuanrong. FE model updating method based on optimization[J].Journal of Vibration and Shock, 2010，22(2):330-340. (in Chinese)

[4] 榮見華，鄭建龍，許飛鴻.結構動力修改及優化設計[M].北京：人民交通出版社，2011.

[5] Salama M, Rose T, Garba J.Optimal placement of exciters and sensors for verification of large dyna-mical systems[C]//Kedward K-T. Proceedings of SDM conference,AIAA-87-0782,1987:1024-1031.

[6] Imamovic N.Model validation of large finite element model using test data[D].London: Imperial College,1998.

[7] Berman A, Nagy E J. Improvement of a large analy-tical model using test data[J].AIAA J,1983,21(8):1168-1173.

[8] 朱宏平，徐斌，黃玉盈.結構動力模型修正方法的比較研究及評估[J].力學進展，2002,32(4)：513-525.

Zhu Hongping, Xu Bin, Huang Yuying. Comparison and evaluation of analytical approaches to structural dynamic model correction[J]. Advances in Mecha-nics，2002,32(4)：513-525.(in Chinese)

[9] 白寶玉，王麗榮.橋梁工程[M].北京：高等教育出版社，2002.

[10] 邵旭東，程翔云，李立峰.橋梁設計與計算[M].北京:人民交通出版社，2006.