小學數學“解決問題”解題習慣的培養

唐麗娟

在一節新課里，同一類型的題目有相對應的解題方法，靠死記硬套公式也可以答對。當題目稍微改變，學生卻一片茫然。原因在于學生沒有養成良好的解題習慣，不能真正理解題意和里面的數量關系。因此，教師在解決問題課堂教學中不但要傳授解題方法，還要重視培養學生良好的解題習慣，否則，學生的解決問題能力不但得不到提高，還不利于學生數學應用意識的養成。

“無論是什么類型的問題，其核心都是需要學生通過觀察、思考、猜測等富有思維成分的活動才能解決的。”因此，可以培養學生以下幾方面的解題習慣，提高學生的解決問題能力。

一、正確的審題習慣——觀察

審題要做到“三部曲”即“讀——動口，想——動腦，劃——動手”相結合的三次讀題。解決問題往往是在生產生活中的實際問題情境，生活化的語言與數學語言差別較大，加上語句長、敘述抽象的特點，使得學生對題意的理解往往產生困難。學生第一次讀題目就要從具體情境里發現數學問題，找出數學信息有意識地重點讀。第二次讀題要重視數學語言的表達，讓學生把題目的條件、問題逐一表述出來，使學生對題目的結構意義達到正確的理解。例如：把一些日常生活中常見的數量概括成數學術語，如時間、速度、路程；單價、數量、總價等等。為了促使學生在讀的同時加強感知，第三次讀題，培養學生在關鍵的、重要的字詞下面“用鉛筆畫”做標記的習慣。例如：分數與百分數解決問題題目中用直線劃出單位“1”的量，圈出已知條件與問題中不統一的數量單位，找出隱蔽的已知條件，去掉多余的已知條件等等。

二、畫圖分析題目的習慣——思考

在解決問題教學中，有些教師只在黑板幫助學生畫圖，不要求學生學會畫圖，學生沒有想象發揮的機會，體驗不到將抽象的實際問題轉化為具體形象的數學問題這一重要環節。一般情況下，許多類型的問題而言，圖形表征是發現解決問題方法的一種有效手段。當學生遇到不會解的題目時，通過以下畫圖方法加深理解題意，在涂涂畫畫中有可能找出解題方法。

1.畫實物圖。低年級的解決問題，往往都是以小動物、花果等編題，教師在教學和作業中，可以要求學生按照題目畫實物圖，再分析列式解答，這樣學生不僅得到畫畫的樂趣，同時也可以得到正確分析解題的方法。在高年級里畫實物圖有助于把問題化繁為簡。例如：雞免同籠的問題，如果使用畫實物圖的方法，學生容易理解。先按照題目數量畫出動物頭，然后每個頭添兩只腳（因為無論是雞還是兔都會有一個頭和至少兩只腳），再把剩下的腳每兩只添到一個頭上，添上兩只腳的頭數就是兔子的數量。

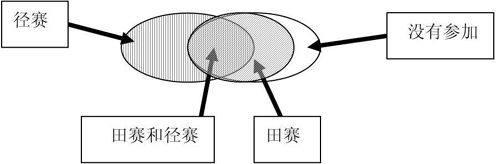
2.示意圖。到了中、高年級，數字比較大，題目難度也加深了，可以用示意圖取代實物圖幫助學生依靠直觀的感知進行抽象思維。例如：三（1）班同學參加學校運動會，參加田賽的有26人，參加徑賽的有30人，以上這兩項都參加的有12人，這兩項都沒參加的有4人，問全班有多少學生？

通過示意圖，數形結合感知情境問題，把多個的已知條件轉化為的直觀表象，學生容易想出多種解題方法：

解法一：26+30-12+4=48（人）

解法二：26+（30-12）+4=48（人）

解法三：26-12+30+4=48（人）

解法四：（26-12）+（30-12）+12+4=48（人）

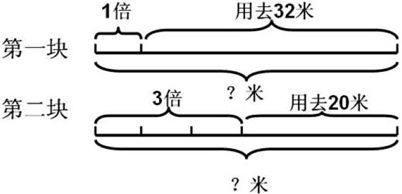
3.畫線段圖。蘇霍姆林斯基指出：“畫線段圖不僅是表象和概念加以具體化的手段，也是一種使學生進行自我智力教育的手段。”線段圖在小學數學應用題教學中起到了奇妙的作用，它可以幫助學生輕松、愉快的學會復雜關系的應用題，是教學中行之有效的教學方法。例如有兩塊同樣長的布，第一塊用去32米，第二塊用去20米。結果第二塊所剩的米數是第一塊的三倍，兩塊布原來各長多少米？

從線段圖容易找出解題的關鍵：第一塊布比第二塊布多用去的正好是第一塊布剩下的（3-1）倍。

解法一：（32-20）÷（3-1）+32

= 12÷2+32

= 38（米）

解法二：（32-20）÷（3-1）×3+20

= 12÷2+32

= 38（米）

三、比較歸類的習慣——猜測

比較歸類出運用相同知識點解答的題目，對表述相近的題目或有多種解法的題目進行比較，抽象概括出事物的本質特點，學會分類、總結其規律，能夠最快地找出解題策略，使解題能力得到提升。例如：歸類出分數和百分數這類型的解決問題，遇到這種題型，首先找單位“1”的量、分量、分率，然后判斷問題求什么？根據等量關系式“單位1的量=分量÷分率，分量=單位1的量×分率，分率=分量÷單位1的量”解題。

總之，教師在數學教學活動中重視學生良好解題習慣的養成，使教學效果事半功倍，提高學生的解決問題能力和數學思維能力，變“學會”為“會學”，為終身學習打下堅實基礎。