簇類特征城市群間的TSP問題研究
王 興
(武漢科技大學信息科學與工程學院,湖北 武漢 430081)
0 引言
旅行商問題(traveling salesman problem,TSP)是指尋求N個城市間遍歷所有城市的最短路徑。該問題是一個經典的組合優化問題,所有的路線組合數為(N-1)!/2。當遍歷的城市數不斷增加,其搜索空間隨著城市數N的增大而迅速增大,并且遍歷所有城市所需時間為問題規模的指數階時間。針對該問題已經提出了多種有效算法,如最近鄰居法、貪婪算法、集群算法等[1-2]。由于群體規模較大,需要對較多的個體進行大量的遺傳和演化操作,從而使得演化運算過程進展緩慢,難以達到相應的計算速度要求。
現實生活中,許多城市在地域上的分布經常呈現區域特征,所以在尋求最優路徑時,應首先提取城市的遍布特征,以相應地減少全局搜索最優解的盲目性;然后再配合使用一些優化算法的組合,從而大量節省最優解的尋解時間。
本文基于上述思想,提出了一種基于平衡聚類的TSP演化算法。
1 聚類算法
根據同類數據集應具有相近特性,而不同數據集在這些特性上差異較大的假定,將所研究的數據集進行分類,這種研究方法稱為聚類[3-4]。聚類是數據挖掘、模式識別等研究方向的重要研究內容之一,傳統的聚類算法在識別數據的內在結構方面往往指導性不強,從而導致聚類算法效率過低。本文為了加強聚類的收斂速度,在使用傳統的聚類算法前,采用城市群稀疏度初提取的方法為以后的聚類提供相應指導。
1.1 城市群稀疏度的提取
隨著當今衛星航拍技術的發展,可以很輕易地得到分布在各個地區的貨物配送城市的地圖。這些地圖是提取城市群稀疏度最后的依據。城市群稀疏度提取的步驟具體如下。
首先將這些貨物配送城市的地理位置量化成具有二維屬性的數據空間S=S1×S2。將每維空間均勻地劃分為p份,則共有p×p個單元網格。所有代表城市的二維地理分布特征數據點將遍布在這p×p個單元網格中。
然后計算每一個單元網格的城市分布稀疏度ρ=nij/N(其中nij為第i行j列的單元網格,N為總城市數量)。與此同時,確定網格密度的閾值,網格單元的密度閾值參數在很大程度上影響算法的聚類質量。在此選取平均密度作為閾值,具體平均密度求解為:

式中:ρij為非空網格密度;M為非空單元網格數。
最后,判別每一非空單元網格的稀疏性。當某一單元網格的密度時,則判定該單元網格為過稀疏網格;當時,則判定該單元網格為稀疏網格;當時,則判定該單元網格為密集網格;當時,則判定該單元網格為過密網格。
1.2 K-均值聚類
K-均值算法是一種得到廣泛使用的聚類算法[4]。它是將各個聚類子集內的所有數據樣本的均值作為該聚類的代表點。算法的主要思想是通過迭代過程,將數據集劃分為不同的類別,使評價聚類性能的準則函數達到最優,從而使生成的每個聚類類內緊湊,類間獨立。
K-均值算法描述如下。
①為每個聚類確定一個初始聚類中心,這樣就有K個初始聚類中心。
②將樣本集中的樣本按照最小距離原則分配到最鄰近聚類。
③將每個聚類中的樣本均值作為新的聚類中心。
④重復步驟②~步驟③,直到聚類中心不再變化。
⑤結束,得到K個聚類。
1.3 平衡聚類算法
根據K-均值聚類的算法原理可知,一旦當聚類的樣本點過多,算法的迭代次數就迅速增加。因此,可以通過提前學習,提取樣本分布特征來指導K-均值聚類,使其成為一種有監督的聚類算法。在此提出平衡聚類算法。
平衡聚類算法的主要思想是以每一個非空單元網格為基準,在其8-鄰域內開通連通區間。若其8-鄰域內存在非空單元網格,則將其連通,并且以新連通的單元網格為基準,開辟新的連通區間直致無法開辟新的連通區域為止。此外,若最終形成的連通域的邊緣存在過密或過稀的單元網格,將影響到聚類中心的預選取,因此將游離該單元網格;若最終形成了K個連通域,將K值作為接下來K-均值聚類的類簇數,并計算每個連通域的城市分布均值,將其作為K-均值聚類的初始聚類中心。
2 免疫遺傳算法
傳統的遺傳算法[5-8]是一種具有“生成 +檢測”的迭代過程的搜索算法。從理論上分析,迭代過程中,在保留上一代最佳個體的前提下,遺傳算法是全局收斂的[9]。然而,在對算法的實施過程中不難發現,兩個主要遺傳算法是模擬生物體的免疫系統算子,其都是在一定發生概率的條件下,隨機地、沒有指導地迭代搜索,因此它們在為群體中的個體提供了進化機會的同時,也不可避免地產生了退化現象。在某些情況下,這種退化現象還相當明顯。每一個待求的實際問題都會有自身一些基本的、顯而易見的特征信息或知識。遺傳算法的交叉和變異算子卻相對固定,在求解問題時,可變的靈活程度較小。這對算法的通用性無疑是有益的,但卻忽視了問題的特征信息對求解問題時的輔助作用,特別是在求解一些復雜問題時,這種“忽視”所帶來的損失往往就比較明顯了。
針對這些問題,提出一種新的算法——免疫遺傳算法(immune genetic algorithm,IGA)[10]。該算法借鑒生物免疫系統的自適應識別和排除侵入機體的抗原性異物等性能,將生物免疫系統的學習、記憶、多樣性和識別的特點引入遺傳算法。在保留遺傳算法優良特性的前提下,該算法力圖有選擇、有目的地利用待求問題中的一些特征信息或知識,以抑制其優化過程中出現的退化現象。
2.1 免疫算子
本文所提出的免疫思想主要是在合理提取疫苗的基礎上,通過接種疫苗和免疫選擇兩個操作步驟來完成的。前者是為了提高適應度,后者則為了防止群體的退化。
①接種疫苗
設個體x,給其接種疫苗是指按照先驗知識來修改x的某些基因位上的基因,使所得個體以較大的概率具有更高的適應度。首先考慮以下兩種特殊情況:其一,若個體y的每一基因位上的信息都是錯誤的,即每一位碼都與最佳個體不同,則對任一個體x,其轉移為y的概率為0;其二,若個體x的每個基因位都是正確的,即x已經是最佳個體,則下一代個體將完全復制上一代的最佳個體基因。此外,設有群體c=(x1,x2,…,xn0),對 c 接種疫苗是指在c中按比例a隨機抽取na=an(0<a≤1)個個體而進行的操作。疫苗是從對問題的先驗知識中提煉出來的,它所包含的信息量及其準確性對算法的性能起著重要的作用。
②免疫選擇
這一操作分兩步完成。第一步是免疫檢測,即對接種了疫苗的個體進行檢測,若其適應度仍不如父代,說明在交叉、變異的過程中出現了嚴重的退化現象。這時該個體將被父代中所對應的個體所取代;如果子代適應度優于父代,則進行第二步處理。第二步是退
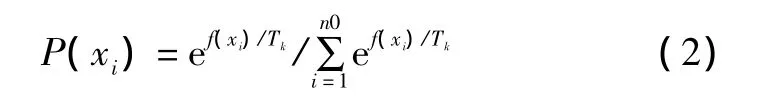
式中:f(xi)為個體xi的適應度;{Tk}為趨近于0的溫度控制序列。
2.2 免疫遺傳算法
免疫遺傳算法流程如圖1所示。火選擇,即在目前的子代群體Ek=(x1,…,xn0)中以概率P(xi)選擇個體xi進入新的父代群體。
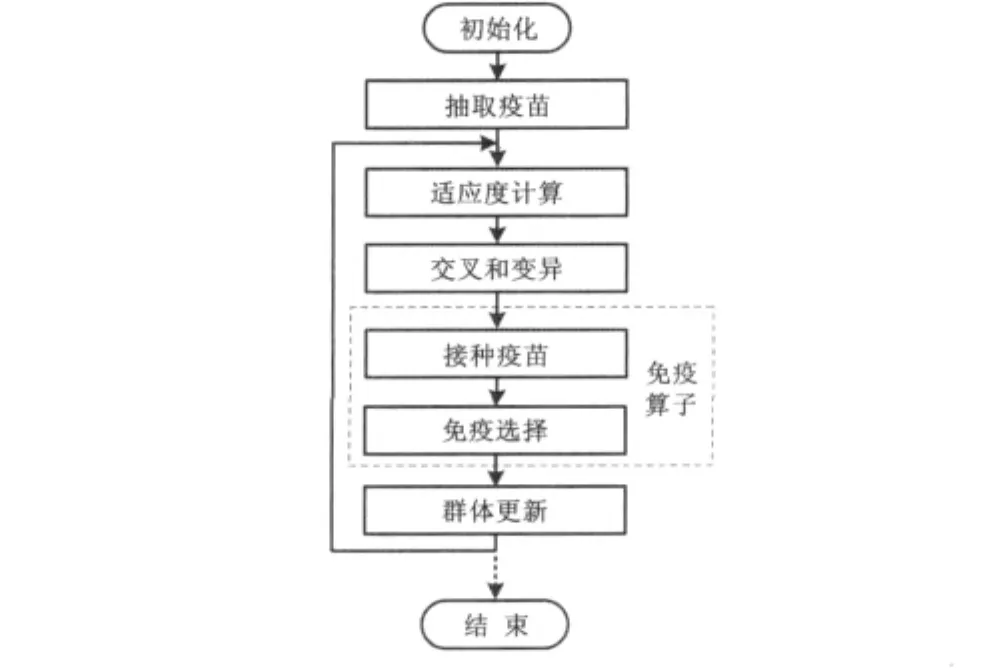
圖1 免疫遺傳算法流程圖Fig.1 Flowchart of the immune genetic algorithm
3 城市群間貨物配送算例
城市群間貨物配送時的路徑選擇問題是一個難解問題,可以使用演化算法求解。當節點很多時,使用演化算法則不可避免地要解決計算速度慢、求解成功率低等問題。
本文提出的基于平衡聚類的免疫遺傳算法大體上分為兩個階段:第一階段是要將所有的城市按照地理分布情況聚成K類,并找出類與類間相隔最近的點;第二階段是在已聚成的類中采用免疫遺傳算法尋求類中的最短城市路徑。具體介紹如下。
第一階段:采用平衡聚類將樣本城市聚類,此處取城市數量為50,聚類數為3。聚類后找出類間最短距離,即找到兩類間相聚最近的兩點。類間最短路徑如圖2所示。
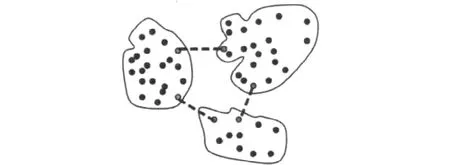
圖2 類間最短路徑Fig.2 The shortest route among clusters
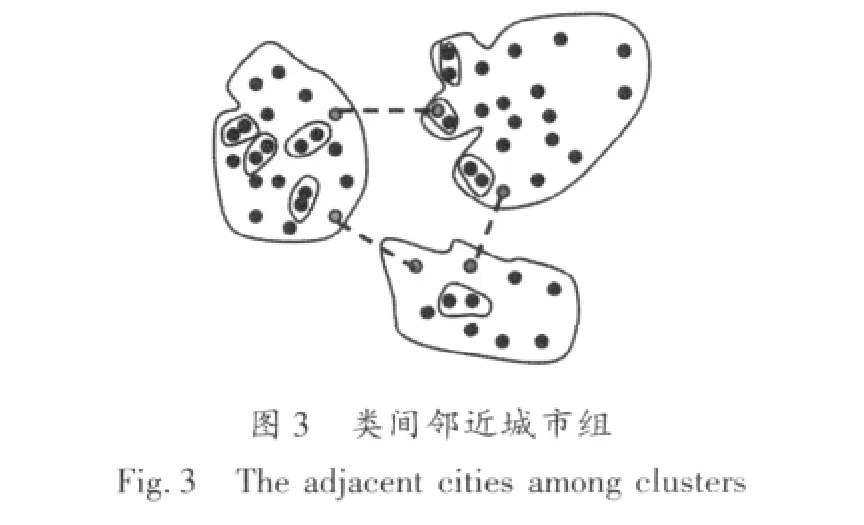
第二階段:在已聚成的每一個類中用免疫遺傳算法尋求最短路徑。此處取類一為例。在確定了首尾城市后,即類一城市群的路線為{c1,…,c2}。根據先驗知識抽取免疫疫苗,類一中相鄰較近的城市組有(c4,c12)、(c23,c9)、(c42,c18)及(c13,c6),其示意如圖 3 所示。因此,經免疫遺傳算法后類一的路徑為{c1,…,c4,c12,…,c23,c9,…,c42,c18,…,c13,c6,…,c2}。以此類推其他幾類內部城市路徑,最終得出所有城市的路徑,其示意圖如圖4所示。
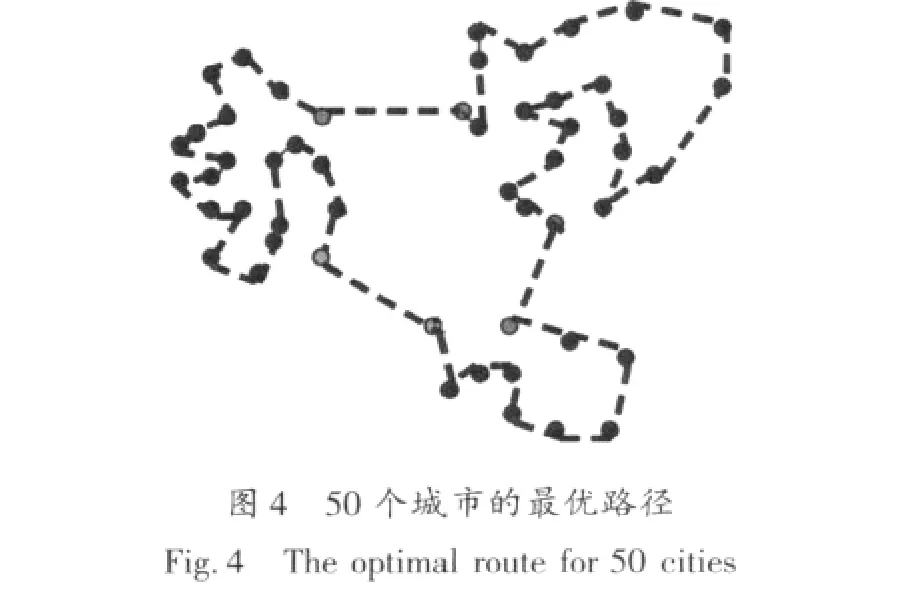
4 算法仿真
采用 CHN144數據,在 Core 2 GHz、0.99 GB 內存的計算機上,分別進行傳統遺傳算法及基于平衡聚類的免疫遺傳算法的仿真。將兩種算法分別仿真5次,每次仿真得到最優解的時間如表1所示。
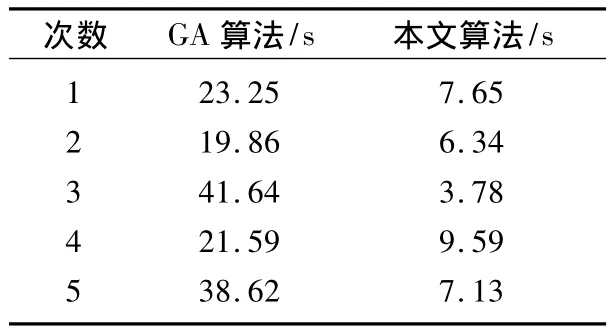
表1 數據仿真結果Tab.1 Simulation result
從表1可知,經5次仿真后,傳統遺傳算法在尋求到最優解時所耗的平均時間為27.59 s,而本文算法平均時間為6.9 s。因此,在具有簇類特征的城市群間尋求最短路徑問題上,基于平衡聚類的免疫遺傳算法的收斂速度較傳統的遺傳算法提高了近3倍。
5 結束語
本文通過聚類與免疫遺傳算法的結合,不僅在具有簇類特征的城市群貨物配送路徑選擇問題上加快了算法的收斂速度,而且還在遺傳算法的基礎上,增加了多樣性保持、免疫記憶和免疫選擇的機制,這樣能使算法收斂速度更快,而多樣性的保持增強了算法全局搜索能力。通過對CHN144數據的試驗后,證明了本文的基于平衡聚類的免疫遺傳算法的可行性,尤其對于具有明顯稠密度的地理分布的大樣本數據,算法的收斂速度較傳統的優化算法有更顯著的提高。
[1]熊盛武,李程俊.基于機群的求解TSP問題的分布式演化算法[J].小型微型計算機系統,2003,24(6):959 -961.
[2]劉宏兵,熊盛武.基于模糊C-均值聚類的TSP演化算法[J].計算機工程與應用,2006(8):32-27.
[3]Sun Y,Lu Y.A scalable grid-based clustering algorithm for very large spatial databases[C]//Proceeding of the International Conference on Computational Intelligence and Security,2006:763 -768.
[4]米源,楊燕,李天瑞.基于密度網格的數據流聚類算法[J].計算機科學,2011(12):54-59.
[5]Huang Z.Extensions to the k-means algorithm for clustering large data sets with categorical values[J].Data Mining and Knowledge Discovery II,1998(2):283 - 304.
[6]陳國良,王煦法,莊鎮泉,等.遺傳算法及其應用[M].北京:人民郵電出版社,1996.
[7]周明,孫樹棟.遺傳算法原理及其應用[M].北京:國防工業出版社,1996.
[8]莉維茨.演化程序—遺傳算法和數據編碼的結合[M].北京:科學出版社,2000.
[9]Rudolph G.Convergence analysis of canonical genetic algorithms[J].IEEE Transactions on Neural Networks,1994,5(1):96 -101.
[10]蔡自興,龔濤.免疫算法研究的進展[J].控制與決策,2004(8):18-23.

