槽式太陽能熱發電聚光集熱器性能計算
崔文智,陳 庚
(重慶大學低品位能源利用技術及系統教育部重點實驗室,重慶 400044)
太陽能熱發電是太陽能發電的一種重要方式,可分為槽式太陽能熱發電、塔式太陽能熱發電、碟式太陽能熱發電[1-3],其中槽式太陽能熱發電站是目前唯一實現了商業化運行的太陽能熱發電系統。聚光集熱器(以下簡稱集熱器)是槽式太陽能熱發電系統的關鍵設備,它的性能直接影響太陽能熱發電系統的整體性能,并與系統的經濟性密切相關,因此很多學者通過各種方法對槽式聚光集熱器進行了大量的研究。
美國加州的SEGS(Solar Electric Generating System)項目中的九座槽式太陽能熱電站主要使用了Luz公司設計的LS系列集熱器,其中LS-2型集熱器使用最多,安裝在多座SEGS太陽能熱電站上,該型號集熱器占SEGS所安裝集熱器數量的65%[4]。美國Sandia國家實驗室使用LS-2型集熱器的實驗臺,在白天輻射正常,集熱器處于工作狀態時對集熱管的熱性能進行實驗研究,并利用實驗數據擬合得到了效率的計算關系式,但該關系式僅以少數幾個實驗數據擬合,適用范圍較小[5],并且需要知道出口溫度。R Forristall[6]在考慮了影響集熱器性能的各種因素基礎上建立了一個較為精確的計算集熱器傳熱及熱損失的模型。梁征和由長福[7]建立了管內流體的一維傳熱模型,研究了太陽能槽式集熱系統的動態傳熱特性。肖杰、何雅玲[8]采用蒙特卡羅光線追蹤法模擬了拋物槽式系統的聚光特性,在此基礎上結合有限容積法研究了真空集熱管表面熱流分布與管內換熱特性。
本文在R Forristall模型[6]的基礎上,不考慮玻璃套管的吸熱量與集熱器支架的熱損失,使用忽略管內摩擦影響的Gnielinski[9]簡化公式計算管內對流換熱,采用整個實驗范圍內都適用的Churchill與Bernstein公式[10]計算管外對流換熱,與Sandia國家實驗室LS-2型集熱器的實驗臺實驗結果比較后表明本文模型優于R Forristall的模型。然后采用該模型計算在不同太陽輻射強度、工質入口溫度、流量組合下,對集熱器的效率與流體工質出口溫度進行計算,求得了多個工況下的集熱器效率與出口溫度。再通過非線性Nelder Mead算法[11]對這些數據進行擬合,得到了集熱器效率與工質的出口溫度的多變量擬合關系式。該關系式可以為其他類型聚光集熱器效率及出口溫度多變量關系式的擬合以及實際工作的太陽能熱電站集熱器場的設計提供參考。
1 計算模型
1.1 建立模型
太陽能聚光集熱器是通過反射器、自動跟蹤等裝置使陽光聚焦到真空集熱管上,將吸收的熱量傳給管內循環的流體工質,集熱管傳熱過程如圖1所示。

為簡化計算,對集熱管作如下假設:聚光反射鏡效率保持不變;忽略集熱管端部波紋管的熱損失;忽略選擇性吸收涂層的熱阻;玻璃的導熱系數不變;玻璃套管內壁面和選擇性吸收涂層為灰體,內部為漫反射和漫射輻射;有效天空溫度低于環境溫度8℃;太陽光線進入拋物槽的入射角為0°。
根據導熱、對流和輻射傳熱定律,以及集熱器傳熱過程,能量守恒方程如下:
真空集熱管吸收的太陽輻射量如式(1)。
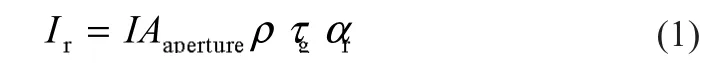
式中:Ir為真空集熱管吸收的熱量,W;I為太陽輻射強度,W/m2;Aaperture為聚光反射鏡開口面積,m2;ρ為聚光反射鏡效率;τr為玻璃管透過率;αr為金屬吸收管涂層吸收率。
金屬吸熱管壁面與玻璃管內壁面及流體工質之間的能量守恒式為:
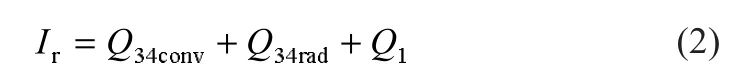
式中:Ir表示集熱管吸收的太陽輻射能量,W;Q34conv表示金屬吸熱管外壁面與玻璃套管內壁面之間的換熱量(近似真空條件下的換熱主要是分子導熱[6]),W;Q34rad表示金屬吸熱管外壁面與玻璃套管內壁面之間的輻射換熱量,W;Q1表示流體工質吸收的熱量,W。
金屬吸熱管管壁與流體工質之間的能量守恒式為:

式中:Q12conv為流體工質吸收的熱量,W;Q23cond為通過集熱管壁面的熱量,W。
金屬吸熱管外壁面3與玻璃套管內壁面4之間的能量守恒式為:
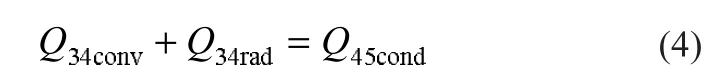
式中:Q45cond表示通過玻璃套管管壁的導熱量,W。
玻璃套管壁面與周圍環境和天空之間的能量守恒式為:
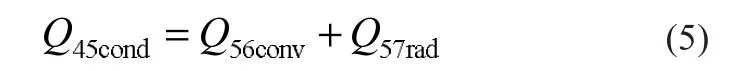
式中:Q56conv表示玻璃套管外壁面與環境空氣之間的對流換熱量,W;Q57rad表示玻璃管外壁面對天空的輻射換熱量,W。
熱損失為:
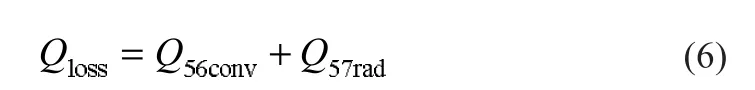
出口溫度為:
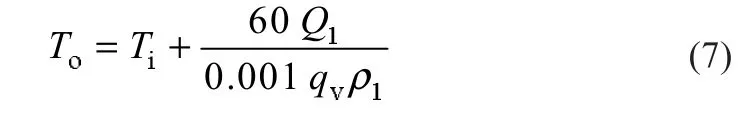
式中:qv表示體積流量,L/min;ρ1表示Ti溫度下的流體工質密度,kg/m3。
集熱器效率為:

式中:I表示太陽輻射強度,W/m2;Aaperture表示聚光器開口面積,m2。
1.2 模型驗證
為便于驗證擬合出來的關系式,本文以Dudley[5]的LS-2集熱器參數為基礎進行多變量關系式擬合,計算中采用的流體工質為導熱油Syltherm 800。
圖2 中,Δt=(Ti+To)/2-Ta,Ti為導熱油入口溫度,℃;To為導熱油出口溫度,℃;Ta為環境溫度,℃。
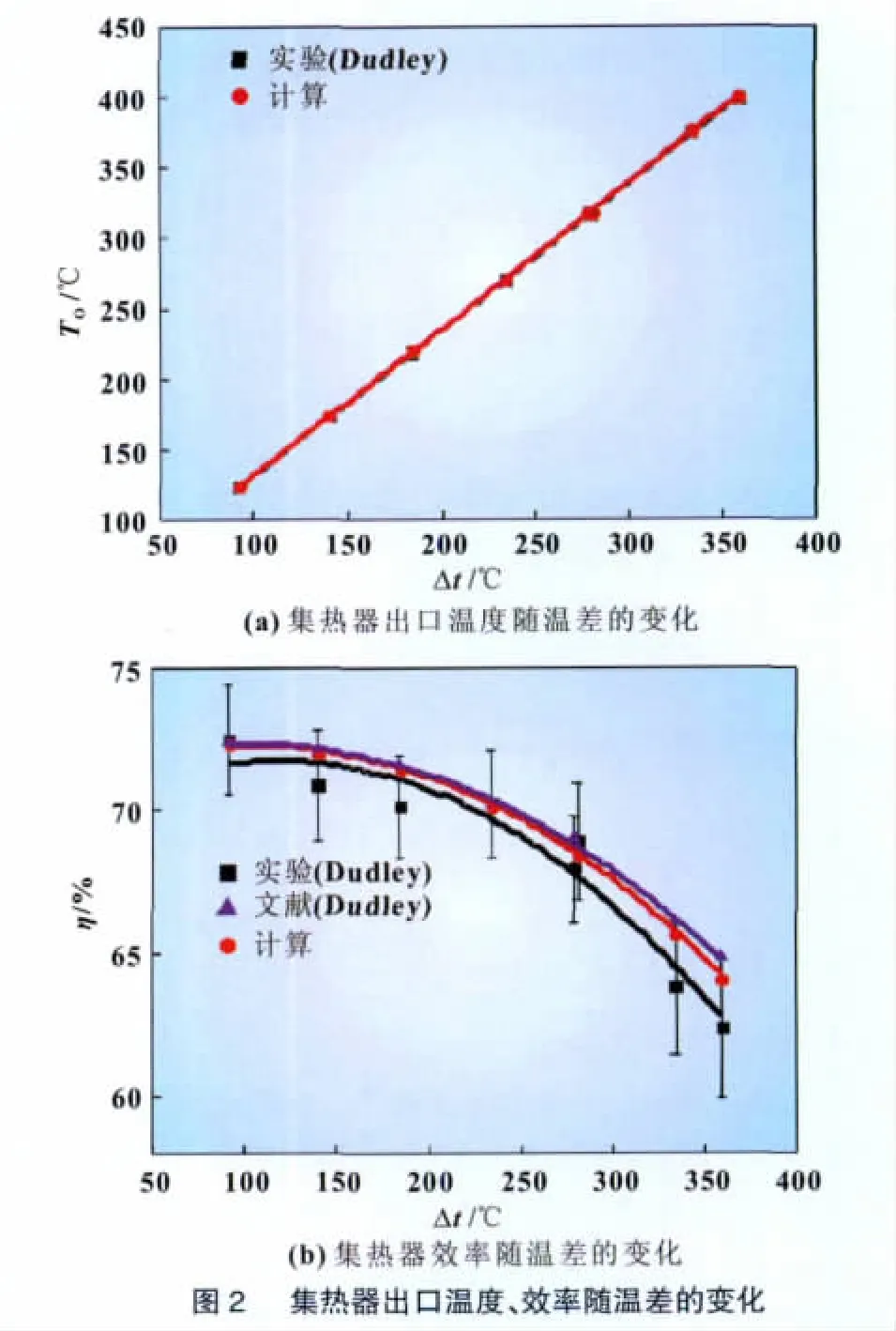
圖2表明,出口溫度與集熱器效率的計算結果與實驗測量結果吻合較好,其中導熱油出口溫度To的相對誤差最大為0.29%;集熱器效率相對誤差最大為2.80%,R Forristall的文獻中所建立的模型效率相對最大誤差為3.95%。本模型除溫差較高的兩個工況點略高于實驗誤差外,其余效率計算值都在實驗誤差范圍之內。因此,總體上本模型優于R Forristall文中的模型。
2 多變量關系式擬合
由模型計算可知,在影響集熱器性能的幾個因素中,太陽輻射強度、工質入口溫度、流量對集熱器效率和出口溫度影響較大,風速及環境溫度影響較小。因此,為了避免擬合出的關系式過于復雜,本文僅對太陽輻射強度I,入口溫度Ti,工質流量qv三個影響因素進行擬合。
2.1 輻射強度的影響
將工質流量、入口溫度設為定值,計算不同輻射強度下的效率η與出口溫度To。
如流量設定為40 L/min,入口溫度為Ti=130℃,輻射強度在300~1000 W/m2范圍內變化,變化間隔為50 W/m2,可得到如下關系式:
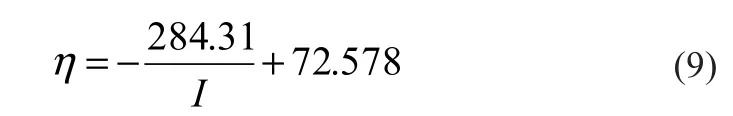
同理,保持流量不變,改變工質入口溫度,可得到不同入口溫度下的效率與輻射的關系式。
2.2 入口溫度的影響
通過2.1節中得到的不同入口溫度下的效率與輻射的關系式,可得到流量為40 L/min工況下的效率與入口溫度、輻射強度的關系式。

同理,改變工質流量,可得到不同流量下效率計算關系式。
2.3 工質流量的影響
根據不同流量下的關系式,可擬合得到效率與輻射強度、入口溫度和工質流量的關系式。

用同樣方法可擬合得到集熱器流體工質出口溫度關系式:
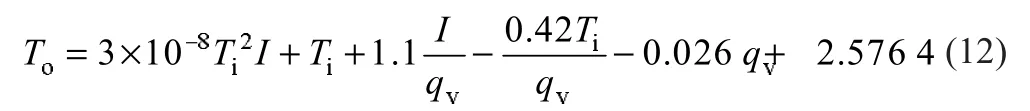
2.4 擬合關系式驗證
為驗證所擬合關系式的準確性,分別計算了在相同運行工況[5](幾何參數和環境參數)下聚光集熱器效率和流體工質出口溫度,并與Dudley的實驗結果及其擬合的關系式進行比較。
由表1可知,本文擬合出的效率關系式與實驗值比較的最小相對誤差為0.221%,最大相對誤差為1.990%,小于Dudley所擬合關系式計算的最大相對誤差5.809%。
由表2可知,出口溫度的擬合關系式結果與實驗結果符合較好,最小相對誤差為0.13%,最大相對誤差為0.38%,誤差較小。總之,以上比較表明擬合結果較好。
3 結論
本文在已有模型的基礎上經過簡化建立了一個比原有模型簡單且精確的模型。利用該計算模型的計算結果,擬合出了聚光集熱器效率和流體工質出口溫度分別與輻射強度、入口溫度、工質流量之間的多變量關系式,誤差較小,擬合效果顯著。
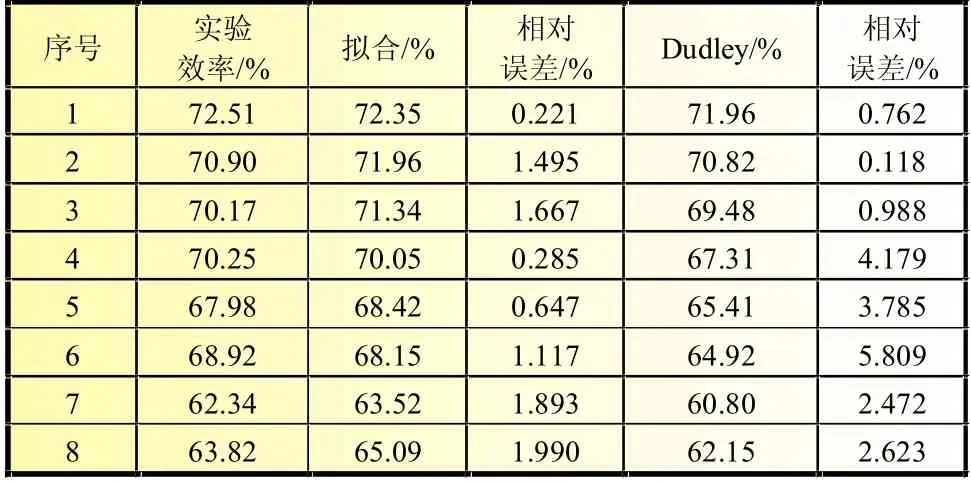
表1 集熱器效率實驗結果與擬合關系式計算結果
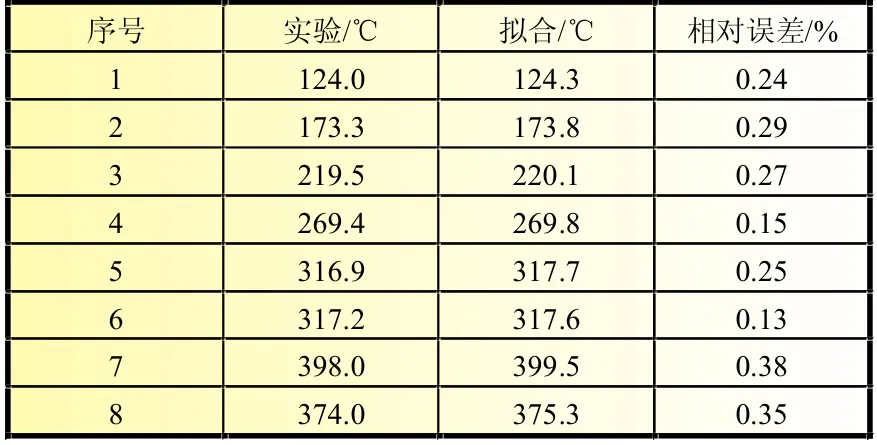
表2 工質出口溫度實驗結果與擬合關系式計算結果
利用所擬合出來的多變量關系式可以計算得到集熱器效率與流體工質出口溫度,便于設定實驗參數以及為進一步提高聚光集熱器及太陽能熱發電站的整體效率提供理論依據,也可以為其他類型的集熱器效率和工質出口溫度擬合提供參考。
[1]袁建麗,林汝謀,金紅光,等.太陽能熱發電系統與分類(2)[J].太陽能,2007(5):29-32.
[2]羅運俊,何梓年,王長貴.太陽能利用技術[M].北京:化學工業出版社,2005.
[3]嚴陸光,陳俊武.中國能源可持續發展若干重大問題研究[M].北京:科學出版社,2007.
[4]MOSS A T,BROSSEAU A D.Test results of a schott HCE using a LS-2 collector[C].Florida USA:ASME 2005 International Solar Energy Conference,2005:737-740.
[5]DUDLEY V,KOLB G,MAHONEY A R,et al.Test results SEGS LS-2 solar collector[R].Albuquerque,NM:SANDIA National Laboratories,1994.
[6]FORRISTALL R.Heat transfer analysis and modeling of a parabolic trough solar receiver implemented in engineering equation solver[R].Golden,Colorado:National Renewable Energy Laboratory,2003.
[7]梁征,由長福.太陽能槽式集熱系統動態傳熱特性[J].太陽能學報,2009,30(4):451-456.
[8]肖杰,何雅玲.槽式太陽能集熱器集熱性能分析[J].工程熱物理學報,2009,30(5):729-733.
[9]GNIELINSNSKI V.New equations for heat and mass transfer in turbulent pipe and channel flows[J].Int Chem ENG,1976,16:359-368.
[10]CHURCHILL S W,BERNSTEIN M.A correlating equation for forced convection from gases and liquids to a circular cylinder in cross flow[J].ASME J Heat Transfer,1977,99(1):300-306.
[11]POWELL M J D.Search on directions for minimization algorithms[J].Mathematical Programming,1973,4:193-201.

