擴展的Sinh-Gordon方程展開法與Kaup-Kupershmidt方程的Jacobi橢圓函數解
王倩,陳曉燕
(西北大學數學系,陜西西安 710127)
擴展的Sinh-Gordon方程展開法與Kaup-Kupershmidt方程的Jacobi橢圓函數解
王倩,陳曉燕
(西北大學數學系,陜西西安 710127)
利用擴展的Sinh-Gordon方程展開法研究了Kaup-Kupershmidt方程的Jacobi橢圓函數解,此方法也適用于求解其他非線性演化方程,從而豐富了方程解的范圍.
擴展的Sinh-Gordon方程展開法;Kaup-Kupershmidt方程;
1 引言
非線性偏微分演化方程出現在數學,物理,化學,生物,通信等廣泛領域,它具有相異于線性演化方程的豐富內涵,與生活聯系更為緊密.在(1+1)維可積模型中,有Kaup-Kupershmidt方程(以下簡稱KK方程):
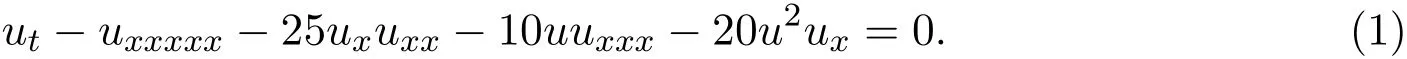
到目前為止,已有很多種方法用來求解KK方程.2003年,文獻[1]通過使用雙曲函數法求得了方程(1)的一些孤立波解;2005年,文獻[2]利用Jacobi橢圓函數的特性和平衡法的思路求得了方程(1)的多種周期解,而文獻[3-5]所提出的Sinh-Gordon方程展開法是一種方便快捷的辦法,已經被用來求解了很多非線性演化方程的Jacobi橢圓函數解.
本文在Sinh-Gordon方程展開法的基礎上,對文獻[5]中變換方法以及所設解中第二項系數函數稍加改變,即擴展的Sinh-Gordon方程展開法[6]再次研究了KK方程,并獲得了由Jacobi橢圓函數表示的方程的通解.進而在極限的形式下,得到了方程相應的三角函數解,從而擴大了解的范圍.
2 擴展的Sinh-Gordon方程展開法
利用擴展的Sinh-Gordon方程展開法求解非線性演化方程的步驟:
步驟一對于含有三個獨立變量x,y,t的非線性演化方程:
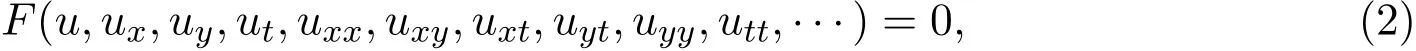

得來,通過平衡(3)式中最高階導數項和起決定性作用的非線性項可以確定n的值.而若參數n恰好不是正整數,則需要再次進行變換u=vn.
步驟三將(4)式代入(3)式,再結合(5)式,可以得到一個關于sinhiω(ξ),coshiω(ξ)的多項式方程,令含有sinhiω(ξ),coshiω(ξ)的各項系數為0,得到關于k,l,λ,A0,Ai,Bi的代數方程組,利用Maple可以解出k,l,λ,A0,Ai,Bi的關系式.
步驟四將得到的k,l,λ,A0,Ai,Bi的關系式代回到(3)式,再利用(4)式的通解,經過分析即可以得到(2)式的Jacobi橢圓函數解.
3 五階KK方程的Jacobi橢圓函數解

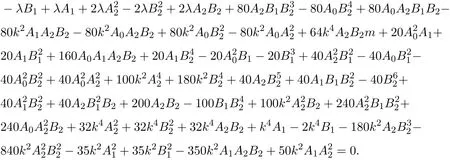
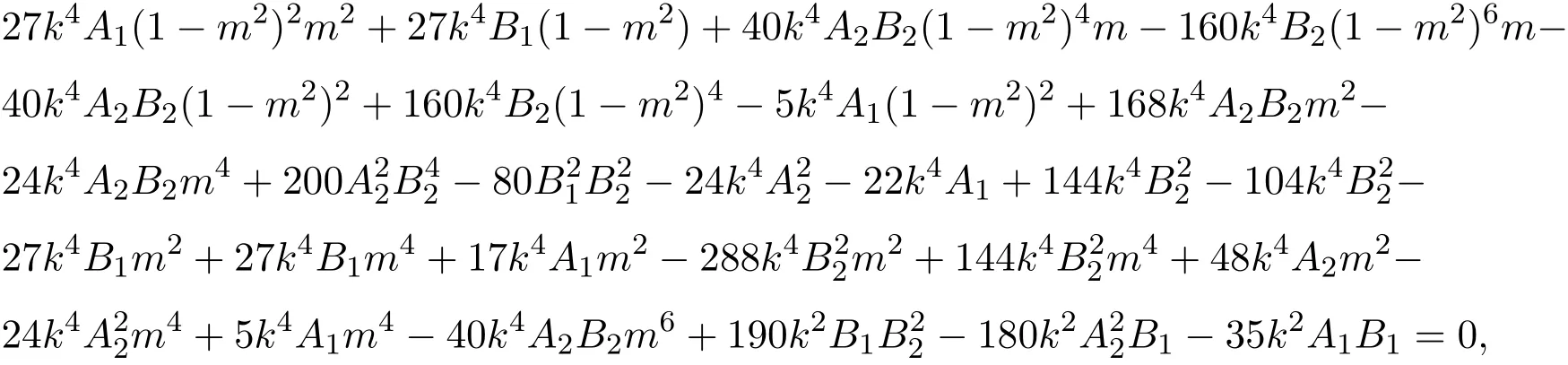


從而將上述解(1)-(6)分別代入(7)式,即可獲得KK方程的對應的(6)式的新的Jacobi橢圓函數解:
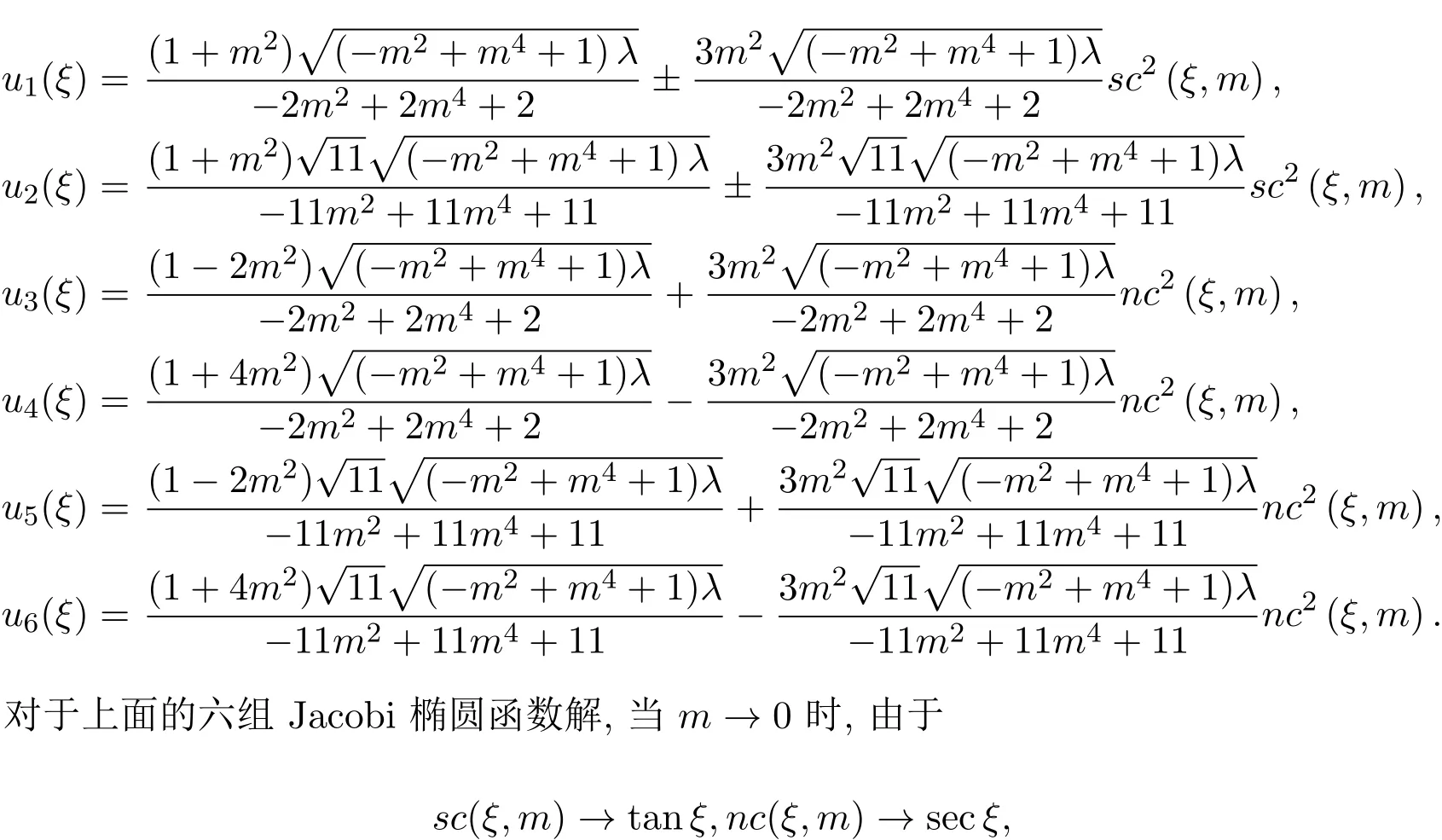
從而得到KK方程相應的三角函數解.
類似地,利用以上步驟還可以對著名方程Benjamine-Ono方程,對稱長波方程和mKdV方程[8]進行求解.用擴展Sinh-Gordon方程展開法求解時方便且快捷,值得在以后的研究中將其推廣,應用到更多的非線性演化方程的求解中.
[1]翁建平.利用雙曲函數法求Kaup-Kupershmidt方程的精確解[J].長沙大學學報,2003,17(6):7-11.
[2]Fu Z,Liu S,Liu Shida.Exact solutions to double and triple sinh-Gordon equations[J].Z.Naturforsch, 2004,59:933-937.
[3]楊先林,唐駕時.非線性演化方程的新Jacobi橢圓函數解[J].動力學與控制學報,2011,2(6):147-150.
[4]劉式適,付遵濤,劉適達.Jacobi橢圓函數展開法及其在求解非線性波動方程中的應用[J].物理學報,2001, 50(11):2068-2073.
[5]翁建平.用Jacobi橢圓函數求非線性方程的解析解[J].安徽大學學報:自然科學版,2005,9(5):36-39.
[6]劉式適,付遵濤,劉適達.非線性波動方程的Jacobi橢圓函數包絡周期解[J].物理學報,2002,51(4):718-722.
[7]Perring J K,Skyrme T H.A model unified field equation[J].Nucl.Phys.,1962,31:550-555.
[8]張善卿,李志斌.Jacobi橢圓函數展開法的新應用[J].物理學報,2003,52(5):1066-1069.
[9]張平.KK方程和改進的Boussineep方程的新精確解[J].數學的實踐與認識,2009,39(4):189-197.
[10]趙云梅,芮偉國.Zhiber-Shabat方程的孤立波解與周期波解[J].純粹數學與應用數學,2008,24(2):283-288.
[11]曹瑞.帶色散項的高階非線性Schrdinger方程的精確解[J].純粹數學與應用數學,2012,1(2):92-98.
Extended Sinh-Gordon equation-expansion method and solutions to Kaup-Kupershmidt equation with Jacobi elliptic function
Wang Qian,Chen Xiaoyan
(Department of Mathematics,Northwest University,Xi′an710127,China)
The paper tends to introduce the extended Sinh-Gordon equation-expansion method which is a convenient tool in solving equations,and the solutions to Kaup-Kupershmidt equation with Jacobi elliptic function can be derived by this method.Furthermore,the related famous equations can also be derived by the method above,which has enriched solutions of them.
extended Sinh-Gordon equation-expansion method,Kaup-Kupershmidt equation, the solutions with Jacobi elliptic function,the solutions with trigonometric function
O175.29
A
1008-5513(2013)02-0159-05
10.3969/j.issn.1008-5513.2013.02.008
2012-11-14.
國家自然科學基金(10671156).
王倩(1989-),碩士生,研究方向:非線性偏微分方程.
Jacobi橢圓函數解;三角函數解
2010 MSC:35J15

