基于Adams的汽車動力總成-整車系統隔振優化設計

潘公宇，嚴 友

(江蘇大學汽車與交通工程學院，江蘇鎮江 212013)

隨著人們的生活品質不斷提升，對車輛乘坐舒適性的要求也越來越高。動力總成因為發動機燃燒和變速器齒輪之間的機械接觸成為汽車振動的主要來源。動力總成和底盤之間依靠懸置元件連接，如何通過合理設置懸置元件的相關參數來提高系統的隔振效率、降低振動傳遞等問題逐漸成為汽車設計人員關注的焦點。

懸置系統的基本功能:①連接動力總成和車架;②承受來自動力總成的往復慣性力和力矩;③隔離發動機與車身之間的振動［1］。

本文應用已測得的動力總成各項參數，建立動力總成-整車動力學模型。運用能量解耦原理，考慮系統各階振動固有頻率的合理分配對優化過程加以約束，利用系統動力學仿真分析軟件Adams對動力總成-整車動力學模型中的懸置系統進行優化設計。

1 動力總成懸置系統模型建立

動力總成通過懸置元件安裝在整車系統中，構成了一個振動系統。要獲得良好的隔振效果，必須對這個系統進行詳細的動力學分析，以獲取最優的懸置元件隔振相關參數及系統的振動特性。一般情況下，動力總成和車身(或車架)的剛度遠大于懸置的剛度，為了簡化分析，常常將動力總成和車身(或車架)考慮成一個具有無限剛度的剛體模型。此時，動力總成懸置系統就簡化成一個6自由度的剛體振動模型，如圖1所示。

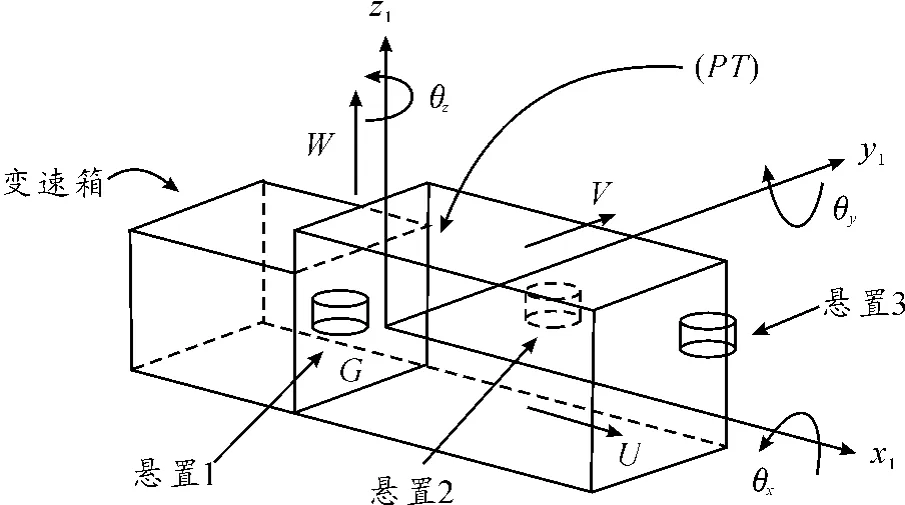
圖1 動力總成懸置系統動力學模型

對圖1的模型進行如下假設:

1)動力總成為帶常系數慣性矩陣的剛體;

2)加載的激振力是周期性簡諧力;

3)懸置近似成具有三向剛度和阻尼彈簧的減震器。

動力總成的運動可以分解為沿X、Y、Z軸的平移運動(平動位移為 x、y、z)和繞 OX、OY、OZ 軸的扭轉運動(角位移為 θx、θy、θz)。廣義坐標向量表示為

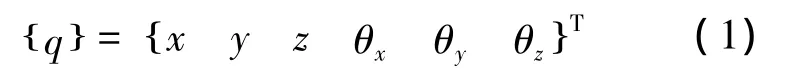
動力總成6自由度振動微分方程為

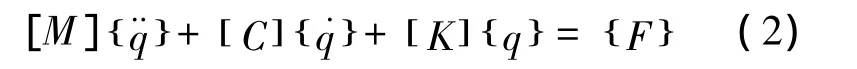
質量矩陣為

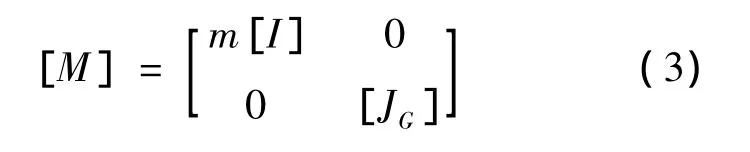
其中［JG］是動力總成轉動慣量矩陣。

剛度矩陣和阻尼矩陣分別為:

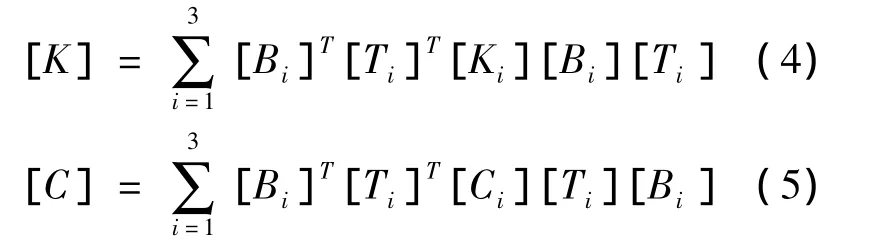
其中:［Ci］、［Ki］分別是阻尼器彈性主軸的剛度和阻尼矩陣;［Bi］、［Ti］分別是位置轉移矩陣和方向轉移矩陣，可以表示為:

其中αi、βi、γi分別表示懸置元件彈性主軸和主坐標軸之間的夾角。

2 能量法解耦原理

對于6自由度振動系統，運動耦合在能量層面的表現是6個自由度方向上均有振動能量的分布，而且分布的百分比并不確定。懸置元件的隔振方向是有限的，振動能量的不集中大大降低了懸置元件的隔振效率。

能量法解耦的原理:在得到6自由度懸置系統各階固有頻率以后，根據在各振動方向上的能量分布來判斷動力總成懸置系統的解耦程度，然后通過修改懸置元件的參數有目的地提高系統在主振方向上的解耦率［2］。在Adams中可以根據式(8)解得系統的振動能量矩陣，記為KE。

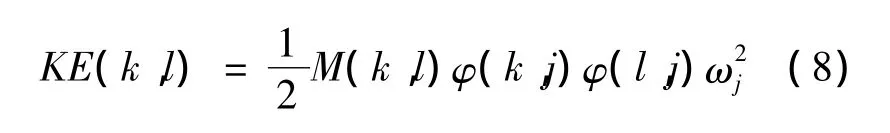
懸置系統總能量近似等于矩陣所有元素之和，記為(KE)j。因此，根據式(9)求出系統以第j階模態振動時第k個廣義坐標的振動能量百分比:

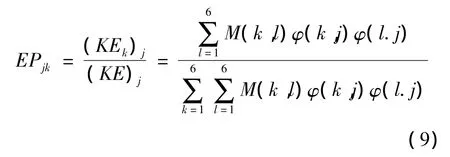
其中:φ(k，j)和 φ(l，j)分別為第 j階振型的第 k 個和第l個元素;M(k，l)為系統質量矩陣第k行、第l列的元素;ωj為第 j階固有圓頻率(k，l，j=1，2，…，6)。

EPjk即為擬求得的振動能量百分比，以此衡量解耦程度的高低。故要提高懸置系統主振方向上的解耦程度(沿z軸及繞x軸的振動)，可通過改變懸置元件的相關參數，使主振方向的振動能量百分比有所提高［3］，并盡量接近于100%。

3 系統振動仿真分析

本文對采用三點懸置布置形式的某型號柴油發動機動力總成進行仿真分析。在Adams/View中建立動力總成懸置系統物理模型［4］，選取地面為廣義坐標平面XOY平面，重力方向為沿Z軸的負方向，基于能量法原理在Adams環境下對系統進行振動仿真。表1是動力總成質量和慣量參數。

表1 動力總成質量和慣量參數 kg·m2

懸置元件近似為三向彈簧減震器，在3個主軸方向上均具有剛度。通過檢測某型號懸置元件的剛度參數對優化前各懸置三向主軸剛度設定的優化值如表2所示。

本文的研究目的是求得系統解耦優化后懸置元件的最佳剛度配置，故以懸置元件的主軸剛度作為設計變量對系統進行優化設計。因此，利用上述初步設定的懸置元件剛度參數對振動系統進行仿真。

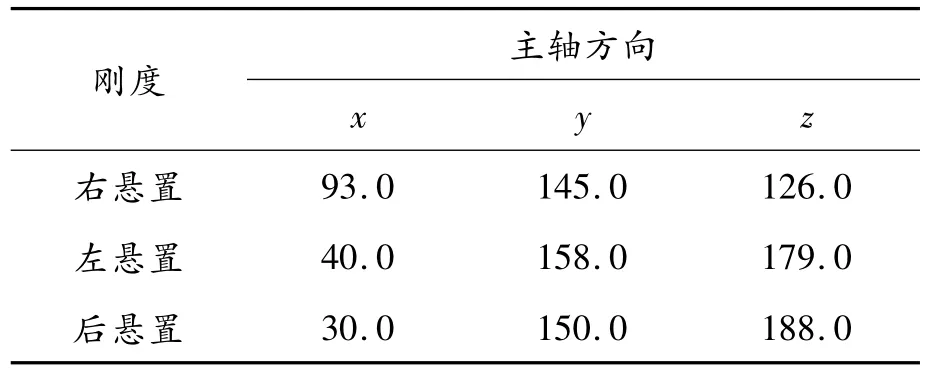
表2 優化前懸置元件主軸剛度 N/mm

仿真分析得到系統振動特性如表3所示。對系統的固有頻率和能量分布進行初步分析，得出以下結果:

1)直列四缸發動機在怠速工況下以2階扭矩激勵為主，其激勵頻率與2階不平衡力相同，在怠速工況下發動機轉速為800 r/min，根據振動分析理論可得其激振頻率為f=2n/60=26 Hz。根據隔振原理可知，要獲得良好的隔振效果，系統固有頻率應該在激振頻率的倍以下，因此，得出固有頻率上限應設定為18 Hz。表3顯示系統的第6階固有頻率為17.51 Hz，說明此系統具有一定的隔振效果，滿足實際需要［5］。

2)從系統振動能量分布來看，表3中動力總成主振方向Z向和θx向的振動能量分別占總振動能量的68.8%和80.2%，說明動力總成懸置系統沿各個方向的振動干擾大，即系統解耦率很低。因此，需要對懸置元件的剛度和阻尼重新設置，以降低振動干擾，提高隔振效率［6］。

表3 優化前動力總成懸置系統振動特性及各方向能量分布

4 懸置系統優化及結果分析

4.1 設計變量選取

在Adams/View中將3個懸置元件的主軸剛度的值取為設計變量(Design Variable)。在Adams中加載振動分析模塊(Vibration)之后，根據初始設定參數新建設計變量，9個剛度變量的變量名分別記為:Stiffness_1X，Stiffness_1Y，Stiffness_1Z……Stiffness_3Z。

4.2 目標函數設置

將系統動能百分比作為優化設計的目標函數，在Adams/View中，用Design Objective命令新建目標函數，選擇View Variable and Vibration Macro一項，在優化目標對話框中選擇Modal Energy。Kinetic Energy選項定義系統沿Z軸和θx方向的動能百分比為目標函數［7］。

4.3 約束條件

為滿足汽車工程實際需要，還須在仿真過程中加入約束條件:

1)懸置系統固有頻率約束

表4 頻率約束范圍 Hz

2)懸置元件主軸剛度約束

懸置剛度過大會使動反力增加，從而加大振動傳遞率;而過小的剛度會讓人感覺懸置偏軟，導致動力總成位移增加，影響懸置元件的使用壽命。故優化時，將各懸置元件的主軸剛度設定在如下范圍:x向，30～200 N/mm;y向，100～300 N/mm;z向，100 ～ 300 N/mm。

4.4 優化計算

設定設計變量、目標函數后進行優化計算。選用 Design Evaluation，選取最近一次仿真結果(Last_Sim)，對目標函數按預設的目標進行優化計算［8］。

4.5 結果分析

經過優化計算得出滿足要求的設計變量值，在物理模型上的反映就是對3個懸置元件的主軸剛度和阻尼進行了重新安排，得出3個懸置點的新一組坐標值，如表5所示。

表5 優化后懸置元件主軸剛度 N/mm

眾所周知，動力總成懸置系統并不是獨立的振動系統，單獨分析動力總成系統的優化結果并不全面，因此，將動力總成布置到Adams整車模型中，加載其他相關參數之后從振動傳遞率、質心垂向位移和加速度的角度來對動力總成-整車系統進行隔振優化設計。

參考前人整車平順性研究時普遍采用的7自由度模型，在Adams中將整車模型和動力總成模型相互結合，兩者在軟件中的安裝示意圖見圖2。

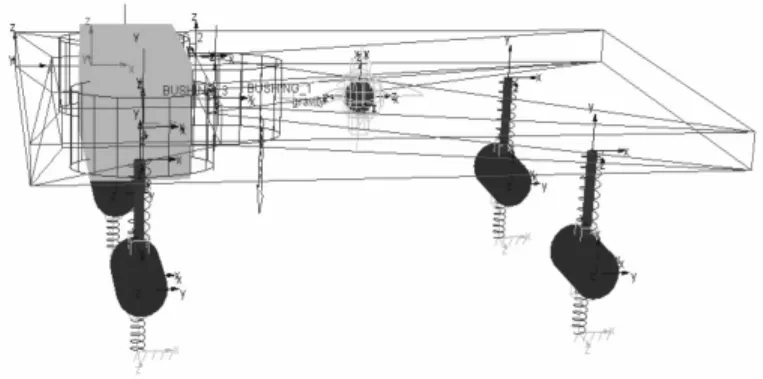
圖2 動力總成-整車物理模型在軟件中的安裝示意圖

定義前軸中心為車輛坐標系原點，動力總成、車身及非簧載質量坐標系均可通過坐標系的轉換獲得。整車模型系統參數設置如表6所示。

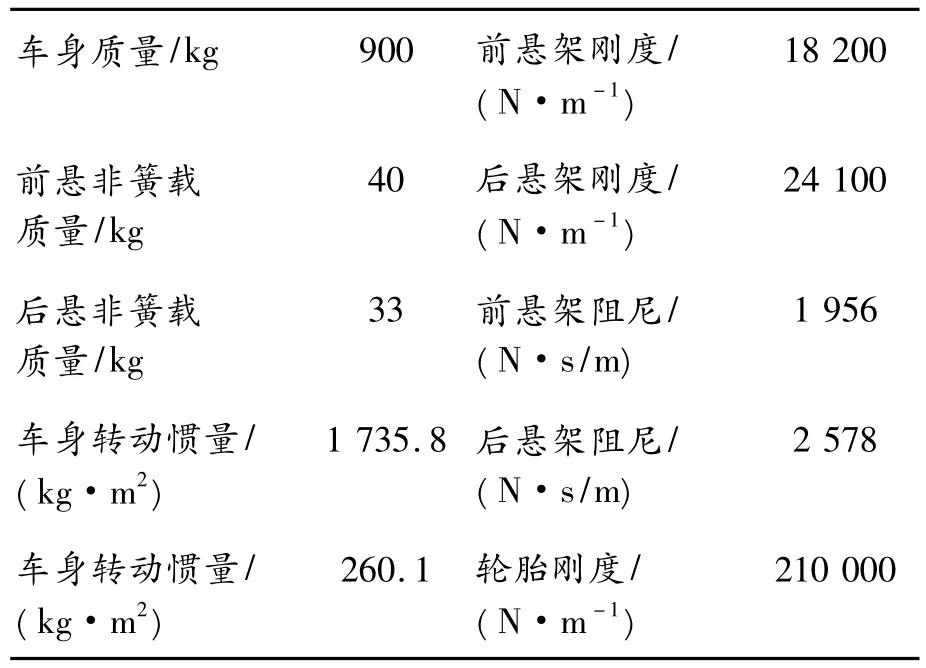
表6 整車模型參數

4.5.1 能量分布分析

系統優化后再次進行仿真，并計算系統各階模態能量分布百分比，結果如表7所示。

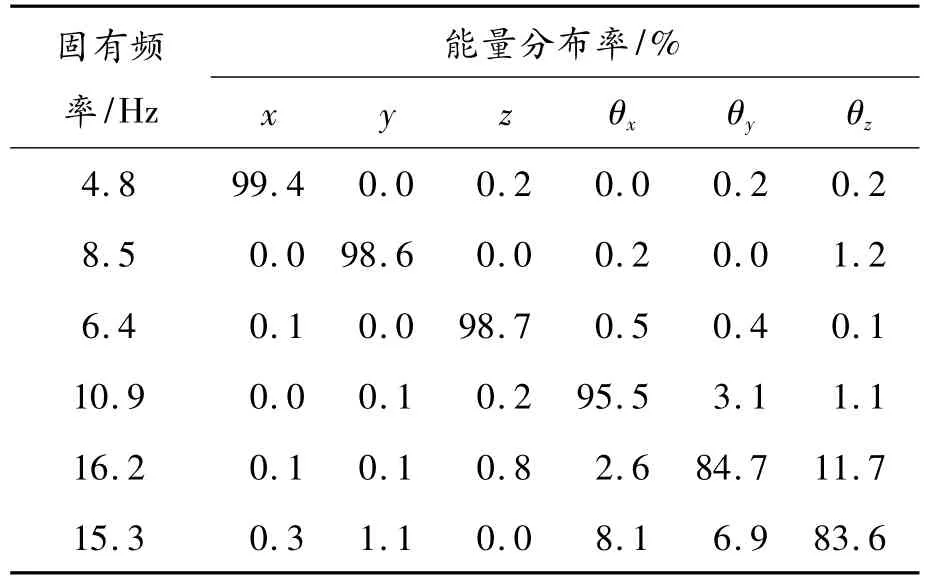
表7 優化后動力總成懸置系統振動特性及各方向能量分布

分析表7可以看出，在主振動方向上—沿Z軸平動和繞X軸轉動，振動能量在總能量中占的比例分別為98.7%和95.5%。此時其他自由度上的解耦率均有較大的提升，整體解耦率有所改善。

4.5.2 優化前后振動傳遞率對比

如圖3所示，優化前的懸置系統垂向振動隔離效果不佳，尤其是怠速階段，左懸置的振動傳遞率高達39%，其他工況下的傳遞率也在21% ～32%，所以各懸置優化前的振動傳遞率均不符合理想隔振的標準。

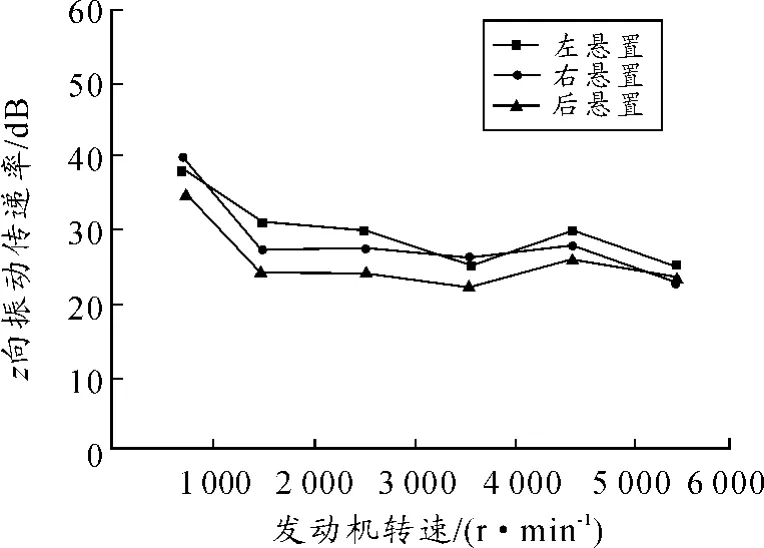
圖3 優化前z向振動傳遞率

如圖4所示，懸置元件主軸剛度優化后，中高轉速工況下，3個懸置點的振動傳遞率均保持在11% ～25%。怠速時，雖然傳遞率較大，但數值均下降到40%以下，能滿足工程應用對隔振的要求。其他工況下，3個懸置也都達到了理想的隔振效果，特別是從各懸置點的振動傳遞率變化趨勢來看，傳遞率波動不大，系統比較穩定。

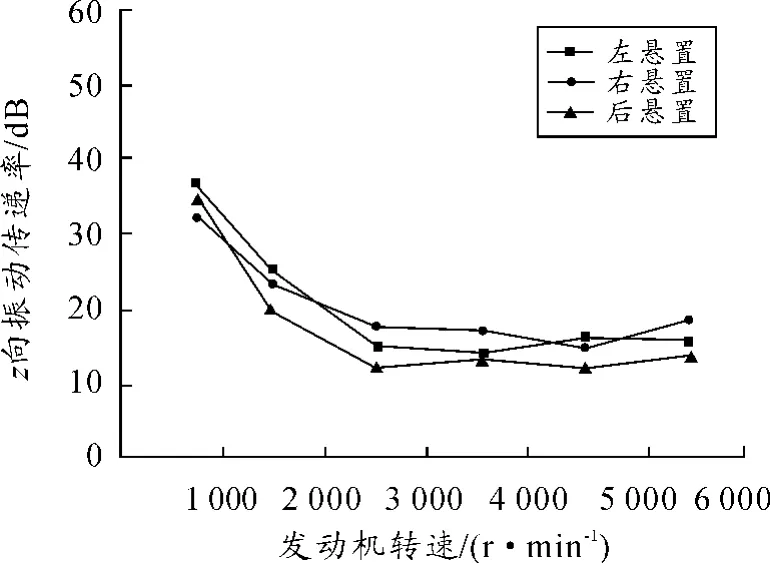
圖4 優化后z向振動傳遞率

如圖5所示，懸置主軸剛度優化前，動力總成在θx方向的振動傳遞率峰值達到27%，表明在θx振動方向上的振動傳遞率過高。

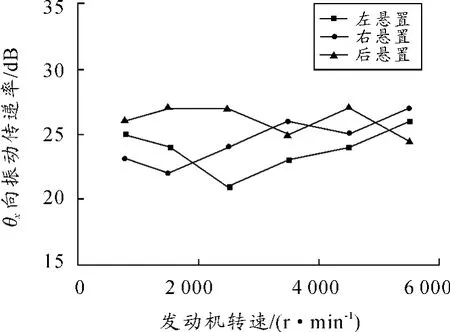
圖5 優化前θx向振動傳遞率

如圖6所示，優化后動力總成振動θx方向的振動傳遞率峰值變為22%，大大減小了動力總成懸置系統在θx向的振動傳遞，對懸置系統的隔振性能有了一定的提升。

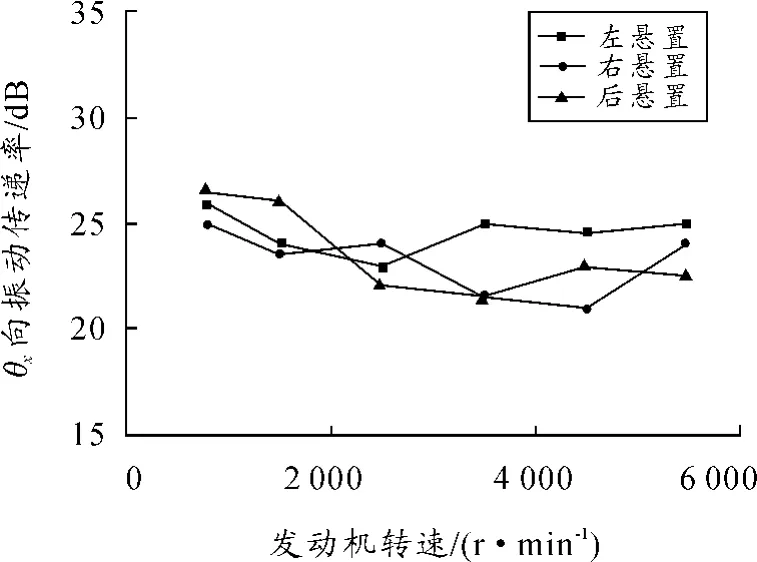
圖6 優化后θx向振動傳遞率

4.5.3 頻域響應分析

如圖7所示，懸置主軸剛度優化前，動力總成質心位移隨著頻率變化而變化的趨勢較快，對汽車減振不利。優化后，動力總成質心位移在中頻振動范圍內保持平穩，說明在此頻率區間內汽車振動幅度較小。而在低頻和高頻時，雖然不平穩，但變化幅度也趨于平緩。

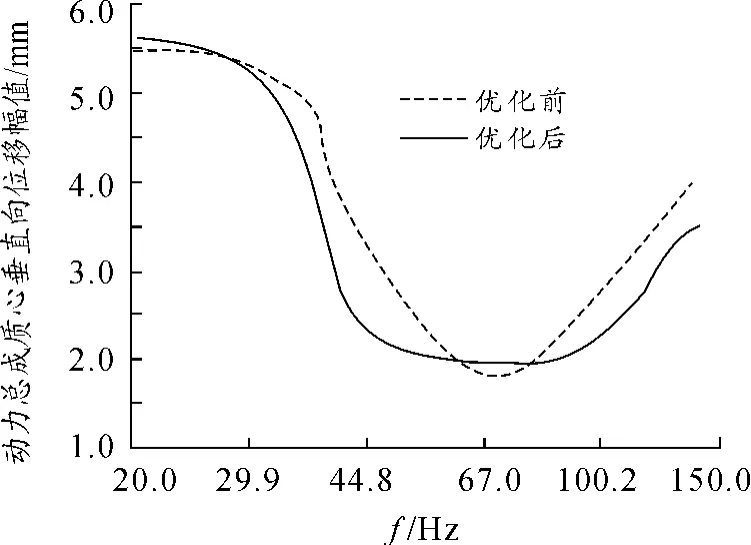
圖7 優化前后質心垂向位移曲線

如圖8所示，優化前動力總成質心垂向加速度波動量比較大，而優化后質心垂向加速度的變化趨勢較平緩，且幅值也有所降低，提高了懸置系統的減振性能。

圖8 優化前后質心垂向加速度曲線

5 結束語

本文利用已經測得的發動機動力總成的各項參數，在Adams環境下建立虛擬動力總成懸置模型。運用能量法解耦的基本原理，以懸置主軸剛度為設計變量、主振動方向(θx，Z)能量百分比為目標函數對系統進行優化設計。在對模型進行優化計算以后，得出整車模型仿真結果，表明優化后重新設計懸置主軸剛度可以有效地提高懸置系統主振動方向的解耦率。證明了解耦效果良好，提高了系統的隔振效率，一定程度上改善了整車的乘坐舒適性。

［1］沈志宏，郭福祥.基于能量解耦法的動力總成懸置系統優化設計［J］.噪聲與振動控制，2010(3)：35-37.

［2］張旭.基于免疫進化算法的發動機懸置系統穩健優化［J］.汽車科技，2012(5)：10-13.

［3］時培成.汽車動力總成懸置系統隔振分析與優化研究［D］.合肥：合肥工業大學，2010.

［4］Ali Hafidi.Vibration reduction on city buses：Determination of optimal position of engine mounts［J］.Mechanical Systems and Signal Processing，2010：2198-2209.

［5］王峰.汽車動力總成懸置系統振動分析及優化設計［D］.上海：上海交通大學，2008.

［6］Johnson Stephen，Subhedar Jay.Computer optimization of Engine Mounting systems［J］.SAE paper，1979(9)：74.

［7］鄭穎，魏朗，鄭顯鋒.基于ADAMS軟件的發動機懸置系統仿真分析［J］.計算機技術與發展，2011，21(4)：231-234.

［8］李增剛.ADAMS入門詳解與實例［M］.北京：國防工業出版社，2006.