偏置正交面齒輪的設計及插齒加工試驗

李天興，劉豫喜，張 華，徐愛軍

(1.河南科技大學機電工程學院，河南洛陽471003;2.河南工程學院機械工程學院，河南鄭州451191)

0 引言

面齒輪傳動是一種圓柱齒輪與圓錐齒輪相嚙合的齒輪傳動形式［1－3］，可應用于正交與非正交場合的傳動。但人們常常忽視面齒輪傳動的另外一種形式—小輪偏置面齒輪傳動［4］。偏置面齒輪是新發展的一種面齒輪傳動形式，偏置能最大限度地拓寬面齒輪傳動的應用領域，為設計者提供更大的發揮空間。因此，偏置面齒輪傳動在機械工程領域具有良好的應用前景。文獻［1－3］對面齒輪傳動的嚙合理論做了研究，從幾何原理的角度獲得了避免面齒輪根切和齒頂變尖的條件。文獻［5－8］由產行齒輪展成面齒輪過程中嚙合角度變化出發，對面齒輪齒寬的研究做了進一步的分析。本文利用齒輪嚙合原理，推導了偏置面齒輪的齒面方程，確定了偏置面齒輪受限的最小內半徑和最大外半徑，提出了偏置面齒輪的加工方法，設計了相應的插齒工裝，最后，在普通插齒機上完成了偏置面齒輪的插齒加工試驗。

1 偏置正交面齒輪齒面方程

1.1 刀具齒面方程

偏置正交面齒輪是由插齒刀范成加工而成，刀具的漸開線齒廓如圖1 所示。

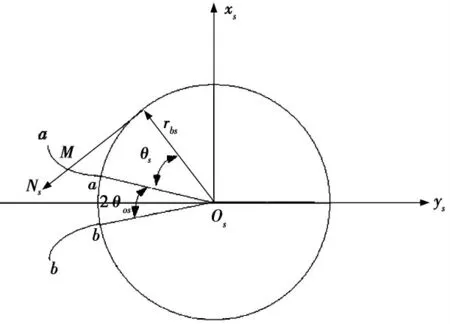
圖1 刀具漸開線齒形

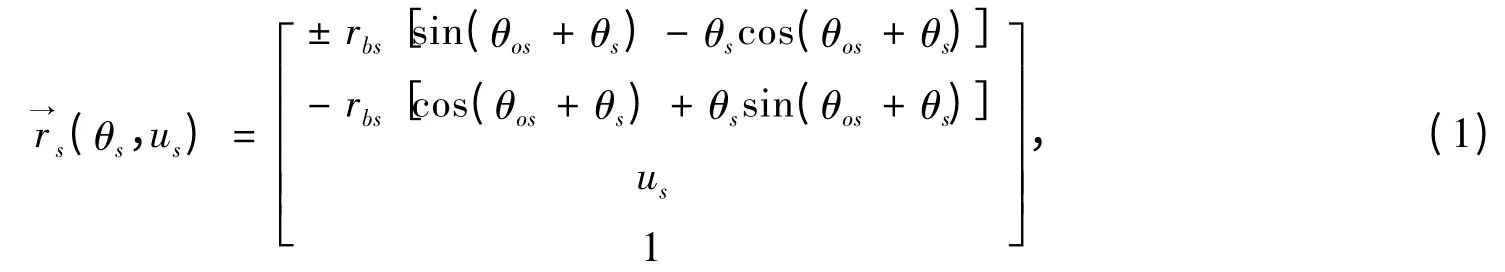
其中，rbs為插齒刀的基圓半徑;(us，θs)為Σs的曲面坐標;θos為確定插齒刀在基圓上的齒槽寬的參數，其值由下式表示:

式中，αo為插齒刀壓力角;Ns為插齒刀的齒數。

刀具的單位法線矢量為:

1.2 偏置正交面齒輪齒面方程

面齒輪齒面Σ 2 由插齒刀齒面Σ S 包絡而成，其齒面方程可由式(4)求出:

式中，M2s為刀具Ss坐標系到被加工面齒輪坐標系S2的變換矩陣;f(θs，φs，us)= 0 為嚙合方程，可由嚙合式求得。

設刀具與面齒輪的接觸點為P，vs為刀具面上p 點的牽連速度，v2為齒面上p 點的牽連速度，把P 點的相對運動速度表示在坐標系Ss下為:

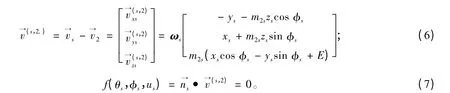
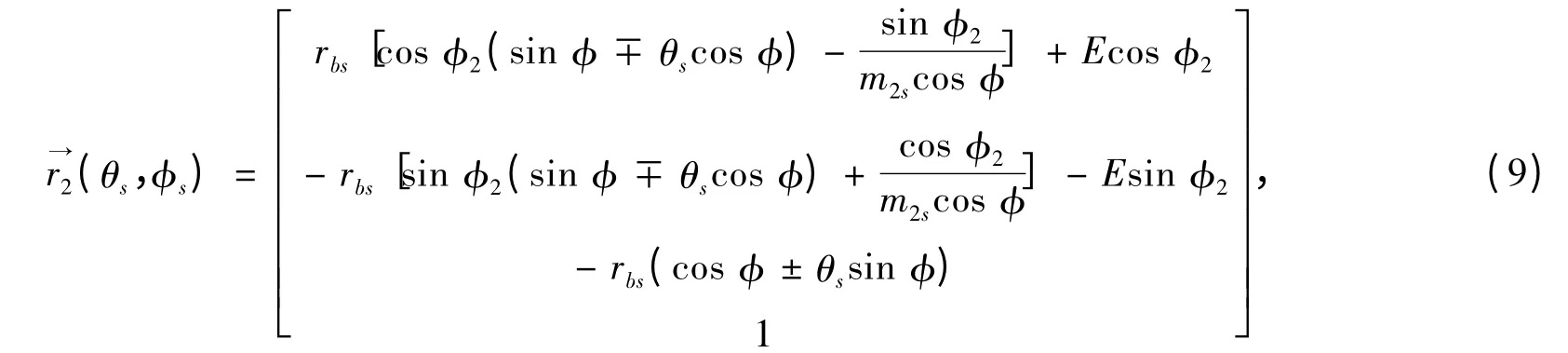
其中，φ=φs±(θs+θos)。

2 面齒輪不發生根切的最小內半徑

根切可以用消除包含奇異點齒面的方法來避免，即

將方程(6)帶入式(10)化簡，再根據嚙合方程得到刀具齒面的限制條件:

將方程(11)中第2 式全微分得:

將方程(11)和(12)聯立可以得到:

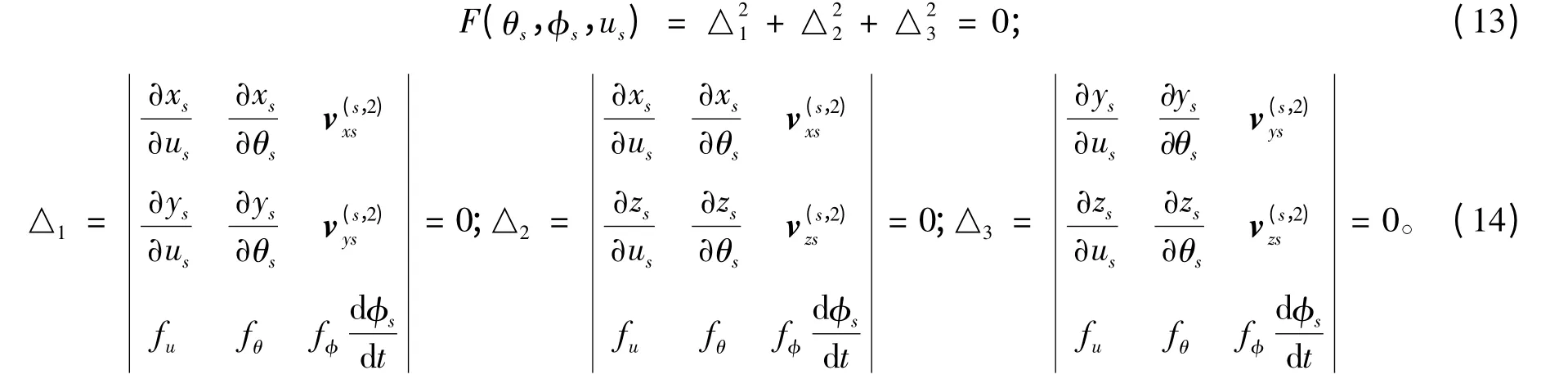
插齒刀的頂圓與根切界限處的交點就是根切極限點，在插齒刀的齒頂，參數θs用下面的方程確定:

式中，ras、rbs分別為刀具的齒頂圓半徑和基圓半徑。

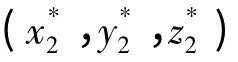
由于偏置正交面齒輪的兩側輪廓是不對稱的，故會有兩個極限值R1a和R1b，在設計中，取兩者的最大值，所以

3 面齒輪齒頂變尖的最大外半徑

把坐標系S2固結于面齒輪并沿z2軸線平移到面齒輪齒頂的位置，建立一新的坐標系Sg，如圖2 所示。將面齒輪的齒面方程轉換到坐標系Sg下，即

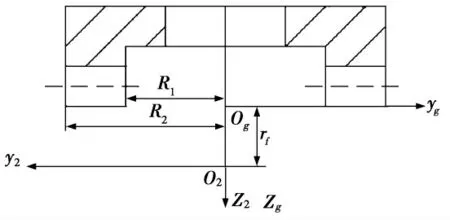
圖2 面齒輪齒面的另一坐標系

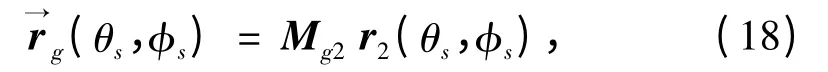
式中，Mg2是從S2到Sg的坐標變換矩陣。

齒頂變尖是指輪齒的兩側齒面相交以后，使得齒頂的厚度等于零或者接近于零，考慮到偏置正交面齒輪兩側輪廓的不對稱性，輪齒變尖的條件為:

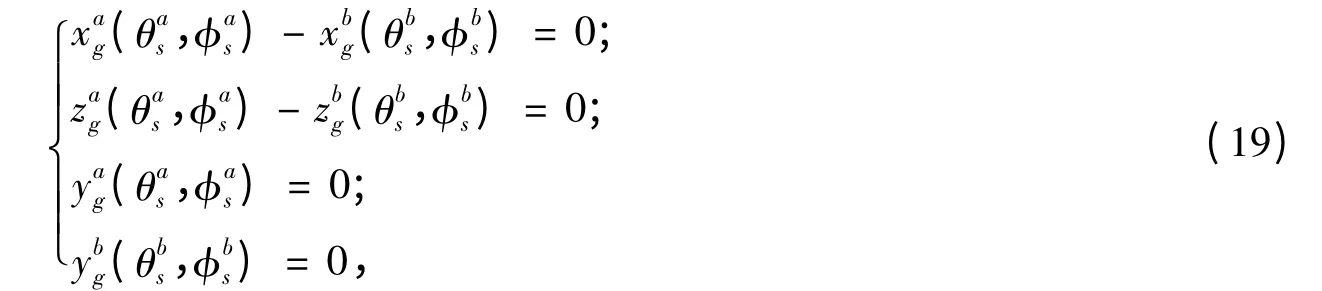
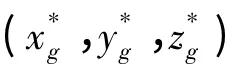
4 偏置面齒輪的插齒加工原理及其試驗

4.1 偏置面齒輪的插齒加工原理

偏置面齒輪的加工除了要求插齒刀插削運動方向同面齒輪軸線垂直外，還要求插齒刀軸線與面齒輪軸線偏置一個距離。插齒刀軸線的偏置是實現偏置面齒輪插齒加工的關鍵。在文獻［9］中，對現有圓柱齒輪插齒機(Y514)，添加了一個錐齒輪傳動，以轉換插齒機傳動鏈的終端，使其由豎直變換到水平方向，實現了正交面齒輪的插齒加工。

圖3 為偏置面齒輪插齒加工原理圖，因為水平軸錐齒輪在同一水平面內的任何方向都可以與垂直方向的錐齒輪嚙合傳動，利用這一特點，讓箱體繞安裝于轉動盤上的垂直軸錐齒輪轉動一個角度γ，錐齒輪的嚙合關系仍不變，面齒輪的軸線將與插齒刀軸線偏離一個距離E，插齒刀插削面齒輪的位置將不再通過面齒輪的軸線平面，而是偏離了一個距離E，這樣即可實現偏置面齒輪的插齒加工。γ 角度根據偏置距離E 的要求進行計算調整。該工裝設計已獲得實用新型專利［10］。

在實際加工中，γ 角的大小與偏置距有如下關系:

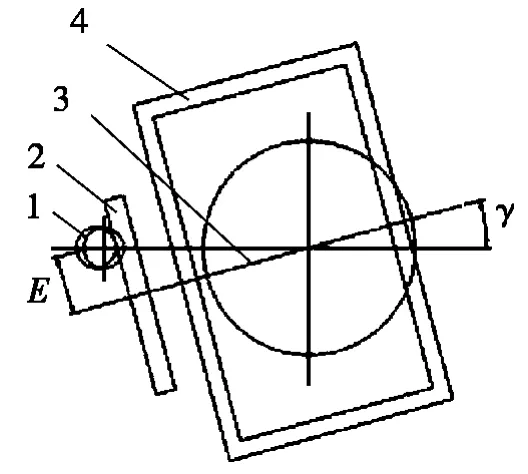
圖3 偏置面齒輪插齒加工原理圖

式中，E 為偏置距;L 為轉盤中心到面齒輪輪坯外端的距離。

4.2 偏置面齒輪的加工與滾檢試驗

插齒刀具齒數Ns=25，面齒輪齒數N2=88，壓力角α0=20°，偏置距E =15 mm，m =3，面齒輪安裝好后的工裝如圖4 所示。圖5 是加工完成的偏置面齒輪在Y9550 型錐齒輪滾檢機上的滾檢照片，得到的接觸印痕如圖6 所示。

圖4 偏置面齒輪插齒加工

圖5 滾檢試驗

圖6 偏置面齒輪上的接觸痕跡

從試驗結果可以看出:輪齒縱向傾斜了一個角度，這正是偏置面齒輪的特點，面齒輪的傾斜齒形保證了與直齒輪圓柱齒輪在偏置位置上的嚙合。因此，利用該方法也可以實現斜齒面齒輪的插齒加工。面齒輪輪齒沒有頂尖和根切現象，齒寬也在計算的范圍內。但接觸印痕質量欠佳，可能因齒面粗糙、工裝誤差引起，但印痕走向符合理論分析。試驗達到了預期的效果，從而驗證了本文所提理論方法的可行性，分析計算的正確性。

5 結論

通過對偏置正交面齒輪齒面方程的推導，得出了齒頂變尖與根切的限制條件。提出了偏置面齒輪的插齒加工方法，在Y514 插齒機上完成了偏置面齒輪的插齒加工試驗。在Y9550 型錐齒輪滾檢機上進行了偏置面齒輪副滾檢試驗。試驗結果達到預期目的，從而驗證了偏置面齒輪設計和加工方法的正確性和可行性。

［1］ David G L，Robert F H，Gregory F H，et al. Evaluation of Carburized and Ground Face Gears［J］. NASA/TM，1999，209188:ARL-TR-1998.

［2］ Hendrik K，Emmeloord N.Face Gear Transmission:United States，4744263［P］.1998－05－17.

［3］ Litvin F L.Gear Geometry and Applied Theory［M］.Englewood Cliffs:Prentice Hall Inc，1994:490－525.

［4］ 魏冰陽，袁群威，吳聰.偏置正交面齒輪的幾何設計及三維造型［J］.河南科技大學學報:自然科學版，2012，33(3):8－11.

［5］ 李龍，朱如鵬.正交面齒輪彈流潤滑分析［J］.機械工程師，2007，36(2):63－65.

［6］ 沈云波，方宗德，趙寧，等.斜齒面齒輪齒寬設計［J］.航空動力學報，2008，23(4):754－758.

［7］ 趙寧，曾曉春，郭輝，等.斜齒面齒輪仿真及其輪齒接觸分析［J］.航空動力學報，2008，23(11):1927－1932.

［8］ 賀鵬，劉光磊.面齒輪數值仿真［J］.科學技術與工程，2007，7(12):2956－2958.

［9］ 姬存強，魏冰陽.正交面齒輪的設計與插齒加工試驗［J］.機械傳動，2010，34(2):58－60.

［10］ 吳聰，魏冰陽，徐增軍，等.一種面齒輪插齒工裝:中國，201220012874.5［P］.2012－07－13.