激光散斑技術中的圖像細分方法

李新忠，臺玉萍，聶兆剛，張利平，李慧娟

(1.河南科技大學a.物理與工程學院;b.化工與制藥學院，河南洛陽471023;2.洛陽市光電功能材料重點實驗室，河南洛陽471003;3.南洋理工大學數學物理學院，新加坡637371，新加坡)

0 引言

激光散斑測量技術［1－8］在測量物體的形變、位移、表面粗糙度等方面有著廣泛的應用［9－11］，而與這些應用緊密聯系在一起的便是測量散斑圖之間的相關系數。在提高散斑測量精度的發展中，圖像細分技術是有利的手段。

圖像細分技術可分為像素級別的與亞像素級別的配準，其中，像素級別的包括:強度相關［12］、相位相關［13］;亞像素級別的包括:強度插值［14］、相位相關插值［15］等。這些方法中，像素級的配準方法精度太低，而亞像素級的配準方法卻過分依賴于插值算法的質量，因此精度得不到保證。

文獻［13］提出了利用相位相關來進行亞像素圖像配準的思想，此種方法不需依靠插值，且能對圖像進行高精度的配準，隨后文獻［16］把這種方法廣泛用于測振工程上。

由于在工程應用上沒有考慮到誤差所帶來的影響，所以不能使測量的精度達到最佳值，文獻［13］中已經提到公式近似，圖像重疊所帶來的誤差以及消除辦法，本文不再敘述。本文主要研究由于降采樣導致頻率域重疊所引入的誤差以及消除誤差的辦法，將其應用于激光散斑測量技術中，并利用相關系數說明該算法的正確性。

1 圖像細分原理及其誤差分析

1.1 相關理論及應用

相關在數學理論和信息處理理論中常用卷積來表示，因此，卷積被稱之為卷積相關。其實圖像相關來源于兩幅圖像f(x，y)和t(x，y)在圖像位分辨率上的卷積關系［17］，

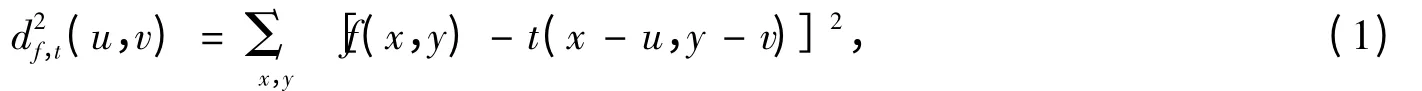
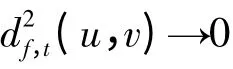
對式(1)進行展開可得到:

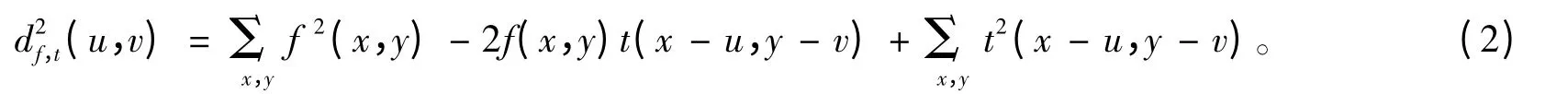
由于t2(x - u，y - v)項為常量，如果f2(x，y)也為常量的話，那么剩下的相關項為:

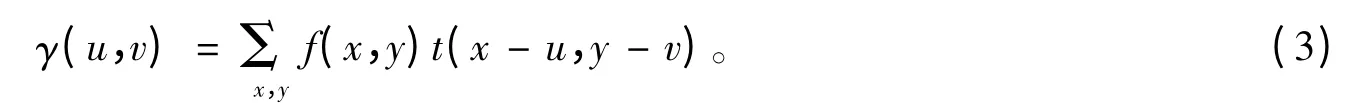
但事實上，f2(x，y)由于激光照射條件的改變而改變，且相關項γ(u，v)隨著匹配模板t(x，y)大小的改變在同一點(u，v)取值也隨之改變。

若此時引入概率統計論中的協方差和相關系數把f(x，y)和t(x，y)當成隨機變量［18］，對它們的相關關系進行描述，則上述的缺點就可以迎刃而解，

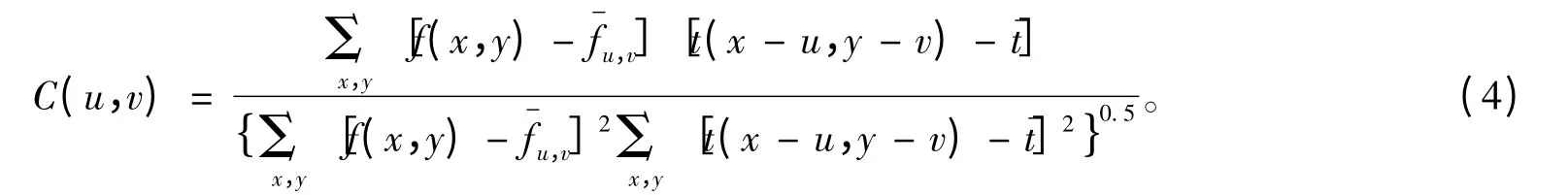
此種對于灰度進行統計描述的方法在圖像處理上稱為“強度相關”，雖然強度相關系數C(u，v)對于計算兩幅圖的相關很有效，但是由于u、v 只能取整數值，所以精度只能達到整像素級，故此技術不能用來測量亞像素級的配準，只能用來作為粗匹配和最后試驗結果的檢驗。即先采取別的辦法對圖像進行亞像素配準，然后再把圖像按照配準的結果進行插值平移，最后，再用強度相關系數計算平移后兩幅圖片的相關系數，從而驗證亞像素配準算法的正確性。

1.2 圖像細分原理

圖像的亞像素級的移動是由于圖像的采樣率低，采樣間隔過大(降采樣)產生的，可以認為當數字圖像采樣間隔減小(過采樣)，就會使亞像素的移動由非整數變成整數，即像素級的移動。例如，對分辨率為128 Pixels×128 Pixels 的圖像移動量為0.5 個像素，當分辨率為1 280 Pixels×1 280 Pixels 時，其移動量為5 個像素。

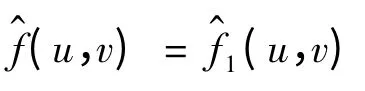
因而，降采樣后的歸一化交叉能量譜為［13］:

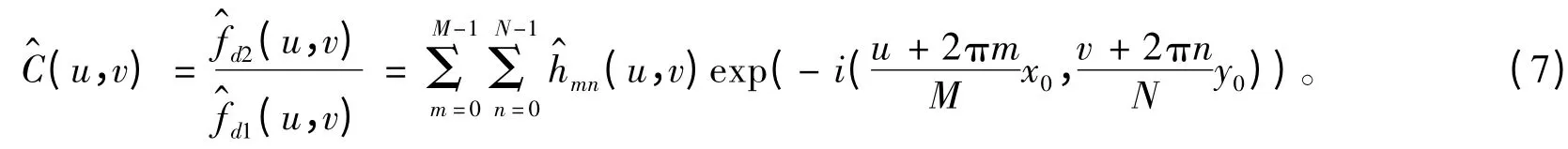
其中，W、H 為降采樣前圖像的寬和高，事實上常用一個sinc 函數來取代式(8)，

考慮

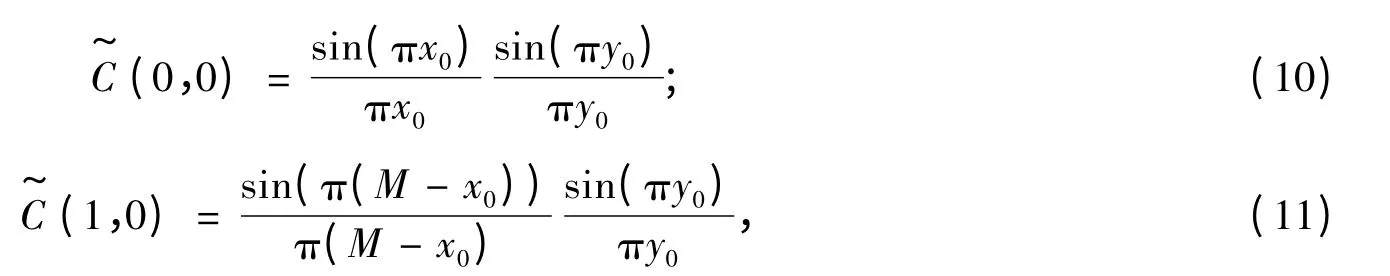
可以得到亞像素移動［20］，

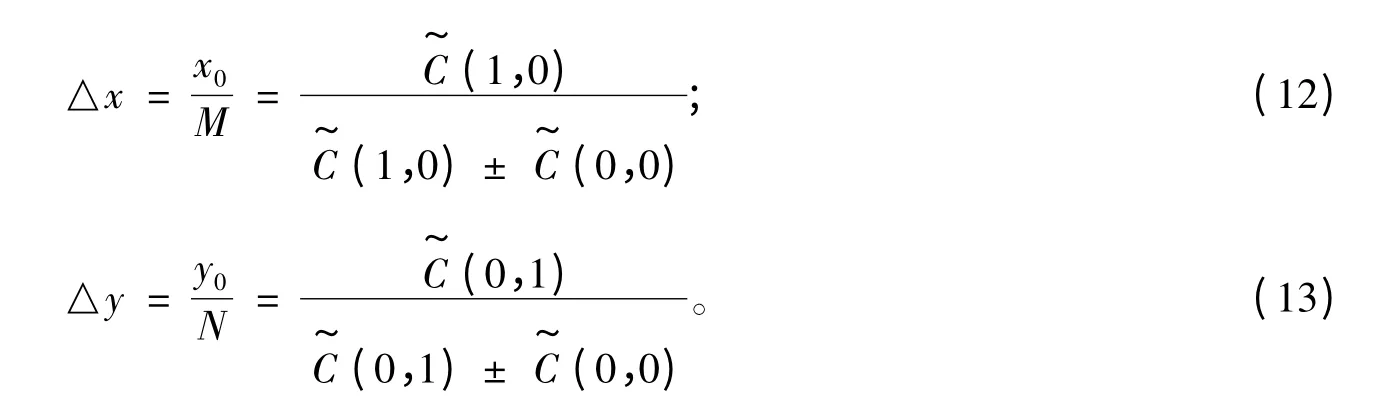
上述兩式的±號主要是決定于M、N 的奇偶性，若為奇數則取正號，若為偶數則取負號。

1.3 圖像細分算法的誤差分析

在1.2 描述的亞像素配準過程中，主要考慮以下3 個方面的誤差源:

(Ⅰ)用式(9)代替式(8)的公式替代誤差。

(Ⅱ)兩幅圖像中非重疊區域帶來的噪聲。

其中，誤差來源(Ⅰ)和(Ⅱ)分別在文獻［20］和文獻［13］中提到，現在考慮誤差來源(Ⅲ)。

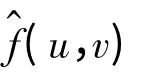
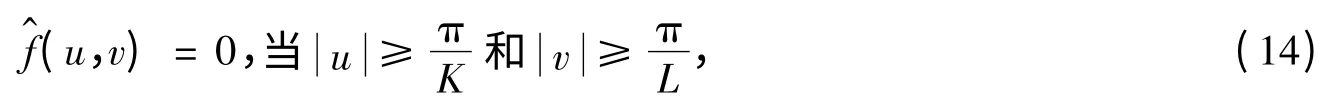
那么，只要當M ＞K 和N ＞L，就能發生頻率混疊的情況，至于混疊的嚴重性就決定于M、N 分別比K、L大的倍數。一旦頻率域出現混疊的情況，那么h^mn(u，v)就不再是理想的帶通濾波器，從而式(7)的逆傅里葉變換就不再是式(8)，從而產生誤差。

假設M = SK 和N = TL，其中S，T ＞1，那么可以通過在交叉頻率譜采用低通濾波來解決頻域混疊所帶來的誤差，其中要濾掉的高頻部分，即濾波條件是:

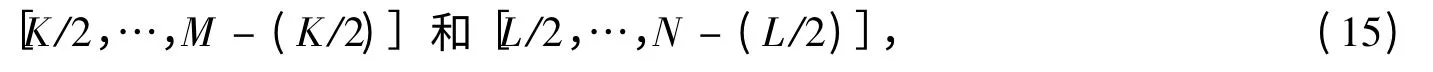
這時式(7)應寫為:

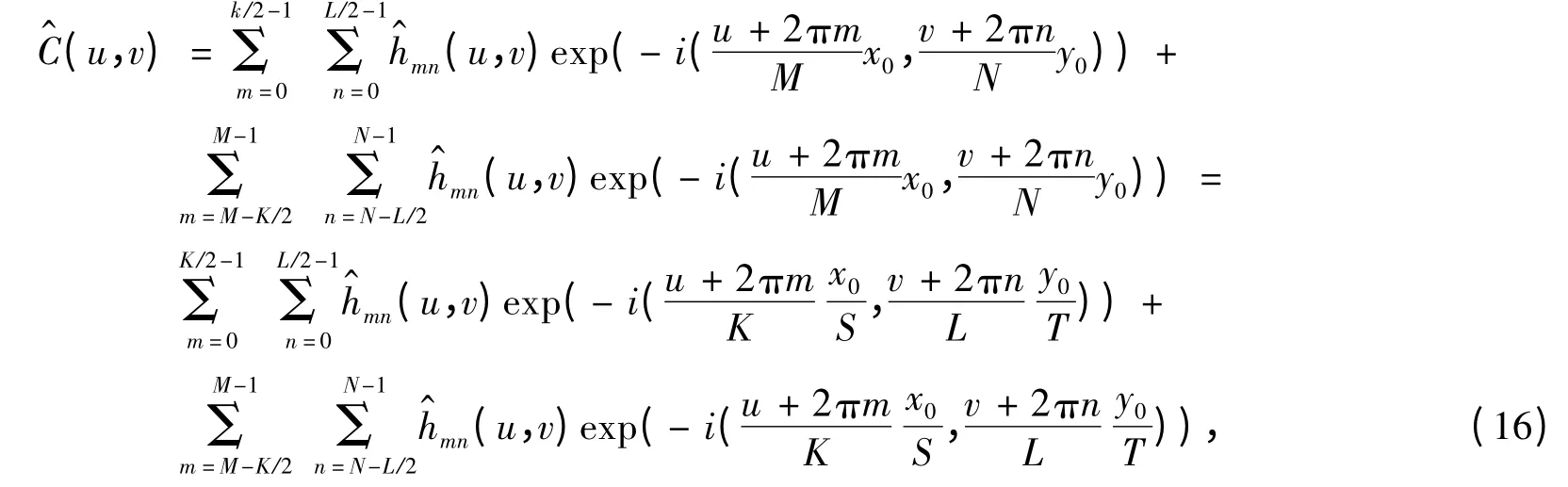
式(16)中的逆傅里葉變換為:

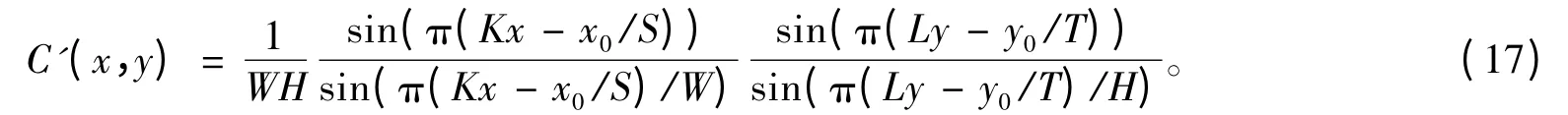
同樣，可以通過C'(1，0)、C'(0，0)、C'(0，1)來求(x0/S)/K = x0/M = △x，同理求得△y。

2 試驗結果及討論

2.1 激光散斑試驗

散斑測量試驗光路如圖1 所示，在圖1 中，RS 為粗糙毛玻璃;GT 為可以使RS 旋轉及測量旋轉角度的旋轉載臺。

當RS 為豎直方向時，用一束與RS 法線方向成θ 角的激光(氦氖激光器)對RS 表面進行照射，然后在另外一個相對的方向用電荷耦合元件(CCD)拍攝RS 表面形成的散斑圖，如圖2 所示。

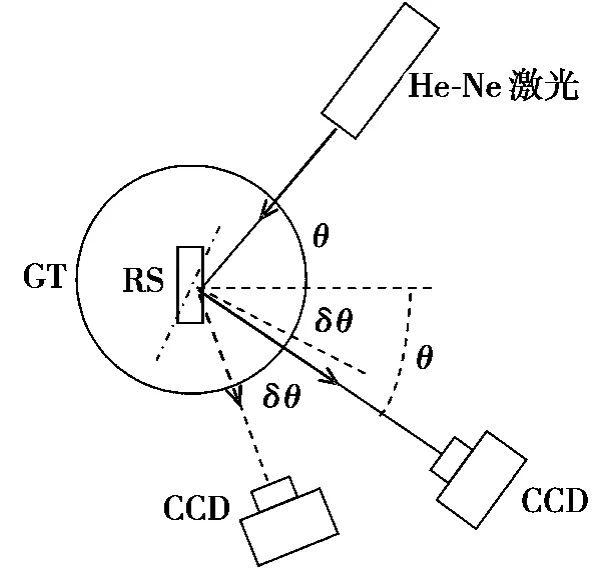
圖1 激光散斑試驗原理圖

然后，讓GT 旋轉δθ 角度，使RS 旋轉同樣的角度，此時把CCD按同樣方向也旋轉δθ 角度，對RS 表面形成的散斑圖進行拍攝，如圖3 所示。由圖3 可以看出:在RS 旋轉δθ 角度后，反射光線應按相同的方向旋轉2δθ，而此時CCD 卻只按相同方向旋轉了δθ，因而能夠拍攝出兩幅散斑圖之間的相對位移。

2.2 試驗結果分析

在對圖像進行配準以前，由于圖片部分區域曝光過強，CCD 產生飽和，因此需要對配準區域進行人工選擇，這里選擇兩幅圖片的左上角坐標(310，0)，右下角坐標(500，250)作為配準區域。

以下是對這兩幅圖像進行分析的步驟:

(Ⅰ)用強度相關對圖像進行粗匹配，得出配準結果為(△x，△y)=(0，0)。

(Ⅱ)強度相關公式(4)計算出圖2 和圖3 兩幅圖像的相關系數c=96.34%。

(Ⅲ)用圖像細分公式(9)～(13)算出配準結果為(△x，△y)=(0.278，0.310)。

(Ⅳ)根據配準結果對圖像進行(△x，△y)=(0.278，0.310)的平移。

(Ⅴ)利用強度相關公式(4)算出平移后圖像的相關系數c=97.67%。

從上面步驟V 得到的相關系數可以看出:在對圖像進行亞像素配準后，圖像相關精度有了明顯的提高，初步顯示出亞像素配準技術的改善效果。

圖2 δθ=0°時的激光散斑圖像

圖3 δθ=1°時的激光散斑圖像

利用濾波條件(15)對圖像進行濾波，嘗試進一步減小誤差。進行以下處理:

(Ⅰ)利用式(15)的濾波帶寬對圖像2 和圖像3 進行濾波。

(Ⅱ)通過式(7)計算濾波后兩幅圖像的交叉能量譜，得到誤差修正模型(17)。

(Ⅲ)利用C'(1，0)、C'(0，0)、C'(0，1)，算出配準結果為(△x，△y)=(0.282，0.320)。

(Ⅳ)同樣根據配準結果對圖像進行(△x，△y)=(0.282，0.320)的平移。

(Ⅴ)同樣的利用強度相關公式(4)統計相關，算出平移后圖像的相關系數c=98.25%。

可以看出:在對圖像進行濾波后，圖像相關精度有了進一步的提高，從而說明了誤差分析的正確性。

3 結束語

通過分析圖像細分過程中誤差產生的原因，引入誤差矯正模型，可以進一步提高圖像配準精度，在試驗上說明了其精度小于0.01 個像素的可能。另外，目前只考慮到頻率域的一階重疊所引入的誤差，若考慮高階的頻域重疊，則將進一步提高配準精度，使此技術在微機電系統中的振動測量精度達到納米水平。

由于在激光散斑檢測技術中，兩幅散斑圖之間除了平動以外可能還存在著轉動，所以在下一步研究中，擬采用互信息配準來對散斑圖進行配準［21］，但散斑圖由于其特殊性，在特征點的提取上有一定的難度，這將成為下一步工作的重點。

［1］ 臺玉萍，李新忠，張利平，等. 磁流體顯示器件光學性能的激光散斑表征［J］. 河南科技大學學報:自然科學版，2012，33(1):92－95.

［2］ 李新忠，臺玉萍，聶兆剛，等.太陽能硅電池表面特性的激光散斑研究［J］.河南科技大學學報:自然科學版，2012，33(4):28－31.

［3］ Li X Z，Tai Y P，Nie Z G.Application of Dynamic Speckle Method Using in Sedimentation Process of Silver Chloride［J］.Optik，2011，122(23):2155－2157.

［4］ Li X Z，Tai Y P，Nie Z G.Digital Speckle Correlation Method Based on Phase Vortices［J］.Optical Engineering，2012，51(7):0770041－0770044.

［5］ Rabal H J，Cap N，Trivi M，et al. Q-statistics in Dynamic Speckle Pattern Analysis［J］. Opt Lasers Eng，2012，50(6):855－861.

［6］ Huang Y H，Liu Y S，Hung S Y，et al.Dynamic Phase Evaluation in Sparse-sampled Temporal Speckle Pattern Sequence［J］.Opt Lett，2011，36(4):526－528.

［7］ Almoro P F，Glückstad J，Hanson S G.Single-plane Multiple Speckle Pattern Phase Retrieval Using a Deformable Mirror［J］.Opt Express，2010，18(18):19304－19313.

［8］ Sendra G H，Rabal H J，Arizaga R，et al. Vortex Analysis in Dynamic Speckle Images［J］. J Opt Soc Am:A，2009，26(12):2634－2639.

［9］ 羅伯特，厄爾夫K.散斑計量學:原理及應用［M］.北京:機械工業出版社，1981.

［10］ Asmad M，Baldwin G，Maczeyzik C，et al. Study of the Surface Roughness in Metals with Different Surface Finishing by Two-dimensional Correlation of Laser Speckle Pattern［C］//Pro SPIE.2004:1495－1500.

［11］ 唐經源，樂開端，張文定.大動態范圍激光散斑位移測量研究［J］.半導體光電，2001，22(2):124－127.

［12］ Goshtasby A，Gage S H，Bartholic J F.A Two-Stage Cross-Correlation Approach to Template Matching［J］. IEEE Trans Pattern Analysis and Machine Intelligence，1984，6(3):374－378.

［13］ Shekarforoush H，Berthod M，Zerubia J.Subpixel Image Registration by Estimating the Polyphase Decomposition of Cross Power Spectrum［C］//Proc CVPR.1996:532－537.

［14］ Dvorchenko V N. Bounds on Correlation Functions with Applications to Registration［J］. IEEE Trans Pattern Anal Machine Intell，1983，5(2):206－213.

［15］ Pearson J J，Hines D C，Golosman S，et al.Video Rate Image Correlation Processor［C］//Proc SPIE.1977:197－205.

［16］ Serio B，Hunsinger J J，Teyssieux D，et al. Phase Correlation Method for Subpixel In-plane Vibration Measurements of MEMS by Stroboscopic Microscopy［C］//Proc SPIE.2005:755－762.

［17］ Lewis J P.Fast Normalized Cross Correlation［J］.Circuits，Systems，and Signal Processing，2009，28(6):819－843.

［18］ 歐俊豪，王家生，徐漪萍，等.應用概率統計［M］.天津:天津大學出版社，1999.

［19］ 奧本海姆，謝弗，巴克.離散時間信號處理［M］.劉樹棠，黃建國，譯.西安:西安交通大學出版社，2001.

［20］ 劉為光，崔江濤，周利華.插值和相位相關的圖像亞像素配準方法［J］.計算機輔助設計與圖形學報，2005，17(6):1274－1277.

［21］ 周永新，羅述謙.基于形狀特征點最大互信息的醫學圖像配準［J］. 計算機輔助設計與圖形學報，2002，14(7):654－658.