對稱邏輯度量次范整子空間及其性質

樓志剛，劉宏昭，胡明娣

1.西安理工大學 機械與精密儀器工程學院，西安 7100482.西安郵電大學 通信與信息工程學院，西安 710121

對稱邏輯度量次范整子空間及其性質

樓志剛1，劉宏昭1，胡明娣2

1.西安理工大學 機械與精密儀器工程學院，西安 710048
2.西安郵電大學 通信與信息工程學院，西安 710121

1 引言

現實世界中的命題是多種多樣的，其中有大量的具體命題是不能簡單地用“真”和“偽”對其可信性作二值判斷的，而應當對它們的可信性程度進行量化判斷。正式基于這種考慮，王國俊教授將程度化思想引入到了數理邏輯之中，建立起了計量邏輯學的基本理論（參看文獻[1-6]）。此后又與概率邏輯學相結合，將隨機化思想引入到了經典的推理模式中（參看文獻[7-8]）。如今已在包括Lukasiewicz，L*，G?del，和Goguen等多種命題邏輯系統中構造出了相應的邏輯度量空間，從而將近似推理引入到了素以嚴格的形式化推理為特征的各種命題邏輯系統之中。值得注意的是，對于邏輯度量空間自身構造的研究已漸次開始被關注（參看文獻[9-14]）。由于對于二值命題邏輯而言，邏輯公式的真度完全由其誘導的布爾函數所決定，而在密碼學中已經對布爾函數有了非常深刻的研究（參看文獻[15]），所以在文獻[12]將密碼學中對稱布爾函數的概念引入到了二值計量邏輯學理論之中，定義了對稱邏輯公式和準對稱邏輯公式，討論了對稱公式集在經典邏輯度量空間中的分布。那么，又進一步思考，在經典邏輯度量空間中，能否構造出類似于Banach空間、Hilbert空間等一樣的空間，能否在這樣的空間中存在一些組合表示等。正是基于這些思考，在本文中引入最簡對稱邏輯公式，定義了邏輯公式的加法和數乘運算。證明了對稱邏輯公式的全體關于所定義的加法和數乘構成線性次范整子空間，并且討論了該子空間的一些簡單性質。

2 基礎知識

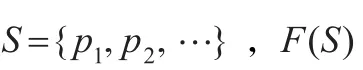
設{0，1}是最簡單的布爾代數，其中：

﹁a=1-a，a?b=max{a,b}，a→b=1當且僅當a≤b（1）則{0，1}也是(﹁，?，→)型代數。

定義2.2[4]設A(p1,p2,…，pn)是含有原子公式p1,p2,…，pn的邏輯公式，用 xi取代 pi(i=1，2，…，n)，并按式（1）理解邏輯連接詞﹁，?，→，則得一布爾函數 fA:{0，1}n→{0，1}，稱為A所誘導的布爾函數。稱 f-1(1)/2n為公式A的真度，記為τ(A)。設A，B為F(S)中的兩個公式，稱

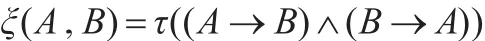
為A與B之間的相似度。再令

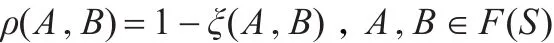
是F(S)上的偽距離，稱(F(S)，ρ)為邏輯度量空間。

已知兩個邏輯公式邏輯等價當且僅當它們之間的相似度為1，或等價地，它們之間的偽距離為0[4]。

注2.1公式A中的原子公式的標號未必是從1到n的連續編號，但設其中最大編號為n，令B=A?(p1?﹁p1)?…?(pn?﹁pn)，則B與A邏輯等價，B中原子公式的標號就是從1到n的連續編號了，所誘導的布爾函數也就可寫為f(x1，x2，…，xn)的形式了。以下凡提到含有n個原子公式的邏輯公式A，恒假定A中的原子公式的標號是從1到F(S)的連續編號。

定義2.3邏輯等價關系≈是F(S)上的(﹁，→)型同余關系，商代數[F(S)]=F(S)/≈是布爾代數，稱為Lindenbaum代數。以[A]記邏輯公式A所在的等價類，定義

則ρ*是[F(S)]上的距離函數，將ρ*簡記為ρ，稱M=([F(S)]，ρ)為經典邏輯度量空間。

3 經典邏輯度量次范整線性空間

定義3.1[11]令M(n)={[A]:A中含有的原子公式包含于{p1，p2，…，pn}}，則

由注2.1容易得到上式成立，并且原子公式 pk∈M(n)當且僅當k≤n。

命題3.1[11]用 B(n)記全體n元布爾函數之集，那么，M(n)與 B(n)之間存在一一對應關系 (n=1，2，…)，且(M(n)，ρ)是經典邏輯度量空間M的有限的閉子空間。

注3.1任取[A]∈M(n)，則φ(A)是一個 n元布爾函數。將其自變量之集{0，1}n中的全體2n個n維向量按字典序從小到大排列為 β1，β2，…，β2n。設φ(A)(βk)=ck，則(c1，c2，…，c2n)是一個 2n維 0-1向量，記為Vec(A)。則φ(A)，[A]，Vec(A)完全相互唯一決定。

定義3.2[11]在{0，1}中規定加法⊕為模2加法，即，0⊕0=0，0⊕1=1⊕0=1，1⊕1=0。將⊕按點式方法作用于V(2n)中的向量的每個坐標，則得V(2n)上的模2加法運算，仍記為⊕，即

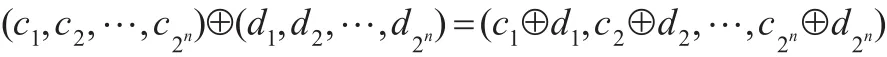
定義3.3[16]設(X,+,θ)是Abel群，Z是整數加群。如果

（1）對于每個序對(m，x)∈Z×X，X中有唯一的元mx與之對應，且滿足：

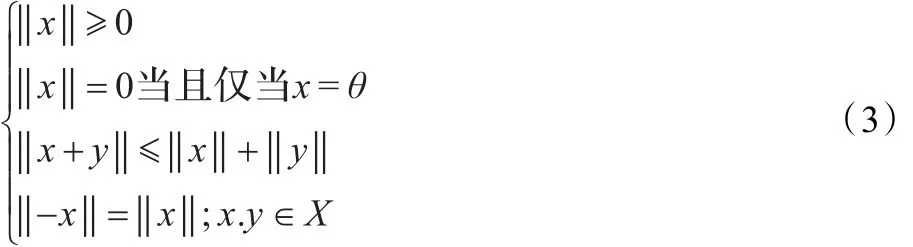
證明 設[A]、[B]是M(n)中的任意兩個元，并且與之對應的Vec(A)=(a1，a2，…，a2n)，Vec(B)=(b1，b2，…，b2n)。

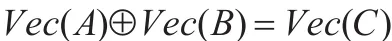
即

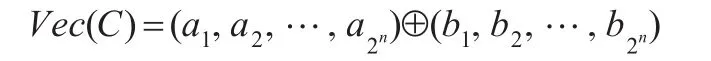
由上定義可見，M(n)中的加法滿足交換律，結合律。

設m是任意整數，定義m[A]=[A]⊕[A]⊕…⊕[A]，m個[A]相加。則易證在M(n)中數乘滿足：m[A]=若m是偶數，m[A]=[A]若m是奇數，m∈Z（4）由式（4）易證式（2）中的各等式對于 x，y∈M(n)和m，n∈Z都成立。

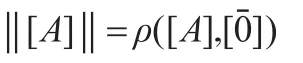
[A]+[B]=[C]當且僅當Vec(A)⊕Vec(B)=Vec(C)此時有：

這里 ρ是經典邏輯度量空間([F(S)]，ρ)的子空間M(n)中的度量函數。顯然

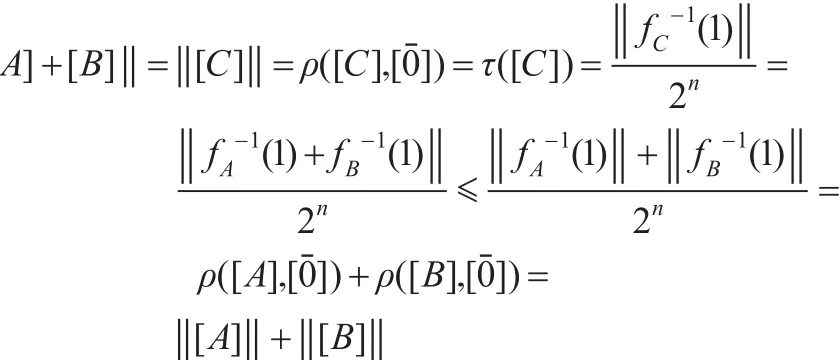
4 對稱邏輯度量次范整線性空間S(n)

定義4.1[15]稱映射 f:{0，1}n→{0，1}為n元布爾函數。設α=(x1，x2，…，xn)∈{0 ，1}n，若 f(α)=1，則稱α為 f的特征向量；稱α中1的個數為α的重量。若一旦{0 ，1}n中某重量為k的向量是 f的特征向量，那么{0 ，1}n中全部重量為k的向量都是 f的特征向量(0≤k≤n)，則稱 f為對稱的布爾函數。以下用N(f)記 f的特征向量的個數，顯然：

注4.1上面關于 f對稱性的表述并非文獻[15]中的原始定義，但易證本文的定義和文獻[15]中的定義是等價的。

定義4.2[15]稱

為n元對稱布爾函數 f的基本表示形式，其中：

注4.2定義4.2中采用的是 f的多項式表示，由于不影響本文的推導，為節省篇幅起見，對什么是多項式表示不作介紹。

定義4.3[15]設A是含有n個原子公式的邏輯公式。如果A所誘導的布爾函數是對稱布爾函數，則稱A為n元對稱邏輯公式。

命題 4.1[12]設 B(p1，p2，…，pm)與對稱邏輯公式A(p1，p2，…，pn)邏輯等價，且 B(p1，p2，…，pm)不是對稱邏輯公式，則n＜m。

命題4.2[12]設二對稱邏輯公式 A(p1，p2，…，pm)與B(p1，p2，…，pn)邏輯等價，且A與B不是重言式，也不是矛盾式，則m=n。

由命題4.1，命題4.2容易得到：

注4.3令S(n)={[A]|A是n元對稱邏輯公式}，那么S(1)?S(2)?…?S(n)?…不成立。例如：A=p1?p2∈S(2)，但是不屬于S(k)，k≠2。

例4.2設Y=M(2)?M(n)（當 n＞2時），容易驗證(M(2)，+，‖?‖)滿足定義4.4的條件，成為Z-子空間。同理，由定義3.1知中有很多個Z-子空間存在。

5 對稱邏輯次范整線性空間的簡單性質

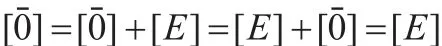
證明 設[A]是n元對稱邏輯公式，假設[B]和[C]都是[A]的負元素，當且僅當滿足：

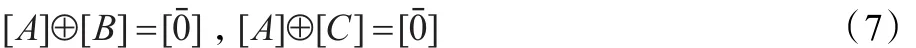
首先由文獻[12]的論證可知[B]和[C]都是n元對稱邏輯公式。其次，式（7）成立當且僅當：

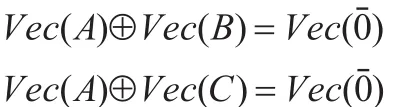
當且僅當對任意的α∈{0，1}n，有：

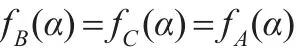
當且僅當：

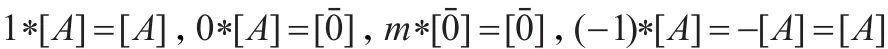
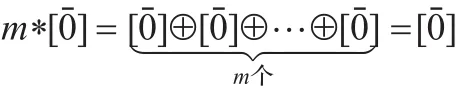
最后，因為1*[A]=[A]，

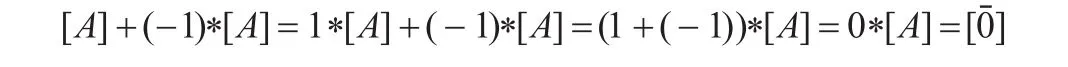
知：

(-1)*[A]=-[A]=[A]

6 結束語

本文繼文獻[11]利用平移群建立M(n)次范整線性空間和文獻[12]引入對稱邏輯公式并討論了對稱邏輯公式及在邏輯度量空間中的分布之后，給出M(n)次范整線性空間新的運算的定義，首次提出對稱邏輯度量次范整線性子空間的概念，并討論了它的簡單性質。這樣的討論使得對邏輯度量空間內蘊結構的建立邁進了新的一步。當然，緊接著可以類似其他賦范空間一樣，給出它的一組基，確定它的維數，探討該空間中是否存在收斂的柯西序列等，這些結果于另文給出。

[1]王國俊.計量邏輯學（I）[J].工程數學學報，2006，23（2）：191-215.

[2]王國俊，宋建社.命題邏輯中的程度化方法[J].電子學報，2006，34（2）：252-257.

[3]王國俊，傅麗，宋建社.二值命題邏輯中命題的真度理論[J].中國科學：A輯，2001（11）：998-1008.

[4]王國俊.數理邏輯引論與歸結原理[M].2版.北京：科學出版社，2006.

[5]WangG J，Zhou H J.Introductiontomathematical logic and resolution principle[M].Oxford，U.K：Alpha Science International Limited，2009.

[6]Wang G J，Zhou H J.Quantitative logic[J].Information Sciences，2009，179：226-247.

[7]王國俊，惠小靜.概率邏輯學基本定理的推廣[J].電子學報，2007，35（7）：1333-1340.

[8]惠小靜，王國俊.經典推理模式的隨機化研究及其應用[J].中國科學：E輯，2007，37（6）：801-812.

[9]Wang G J，She Y H.A topological characterization of consistency of logic theories in propositional logic[J].Mathematical Logic Quarterly，2006，52（5）：470-477.

[10]胡明娣，王國俊.經典邏輯度量空間中的反射變換[J].陜西師范大學學報：自然科學版，2009，37（6）：1-4.

[11]王國俊，胡明娣.經典邏輯度量空間中的模2次范整線性空間結構[J].電子學報，2011，39（4）：899-906.

[12]胡明娣，王國俊.對稱邏輯公式在經典邏輯度量空間中的分布[J].電子學報，2011，39（2）：418-423.

[13]胡明娣，樓志剛.經典邏輯度量空間中的邊角關系[J].西北大學學報：自然科學版，2011，41（2）：206-211.

[14]王慶平，王國俊.對稱邏輯公式在L_3_邏輯度量空間中的分布[J].計算機學報，2011，34（1）：105-114.

[15]溫巧燕，鈕心忻，楊義先.現代密碼學中的布爾函數[M].北京：科學出版社，2000.

[16]王國俊，王偉.經典邏輯度量空間[J].數學學報，2001，44（1）：159-168.

LOU Zhigang1,LIU Hongzhao1,HU Mingdi2

1.School of Mechanical and Precision Instrument Engineering,Xi'an University of Technology,Xi'an 710048,China
2.School of Telecommunication and Information Engineering,Xi'an University of Posts&Telecommunications,Xi'an 710121,China

Addition and number multiplication are defined in the classical logic metric space,and the norm are introduced by using the degree of the formulas.It is proved that the classical logic metric space builds a Z（2）-normable linear logic space.The concept of a Z（2）-normable linear logic sub-space is introduced,according to the definition,it is proved that the set of n-symmetric logical formula constitutes the a Z（2）-normable linear logic sub-space.Some basic characters of the sub-space are discussed.

symmetric Boolean function；symmetric logic formula;Z（2）-normable linear logic space;norm;symmetric logic Z（2）-normable linear sub-space;classical logic metric space

在經典邏輯度量空間中定義了加法和數乘運算，利用公式的距離引入了經典邏輯度量空間中的范數的概念，從而證明了經典邏輯度量空間作成線性次范整空間。引入了次范整線性子空間的概念。證明了n元邏輯公式之集中的對稱邏輯公式子集構成了次范整線性子空間，并討論了該子空間的簡單性質。

對稱布爾函數；對稱邏輯公式；次范整線性空間；真度；對稱邏輯子空間；經典邏輯度量空間

A

O159

10.3778/j.issn.1002-8331.1112-0131

LOU Zhigang,LIU Hongzhao,HU Mingdi.Classical symmetrical logic metric sub-space and its properties.Computer Engineering and Applications,2013,49（5）：40-43.

陜西省基金項目（No.102-00X903）。

樓志剛，男，在讀博士研究生，講師，主要研究領域為故障識別、數據分析、模糊控制；劉宏昭，男，教授，博士生導師，主要從事機電系統建模、測試及控制、機構學及CAD、機械動力學研究；胡明娣，女，副教授，主要研究方向為數理邏輯、模糊控制。

2011-12-08

2012-03-13

1002-8331（2013）05-0040-04

CNKI出版日期：2012-05-21 http://www.cnki.net/kcms/detail/11.2127.TP.20120521.1142.075.html