微小深度尺寸測量系統的誤差與測量不確定度分析

齊皇仲，葉懷儲，陳 歡，潘 璐，李 建

（浙江省計量科學研究院，浙江 杭州 310013）

0 引 言

項目中自制的測量系統包括電子目鏡、光切顯微鏡、三軸運動平臺以及上位機。由于該測量系統定位于工業現場測量，電子目鏡和上位機可以實現電腦讀數以提高測量速度，光切顯微鏡提供精準的測量方法，三軸運動平臺模擬了工業環境中的取樣送樣環節，整個測量過程盡可能地還原生產現場，實現全自動測量。現場測量環境相對于實驗室較為復雜多變，因此對其誤差來源及測量不確定度的分析尤為重要。

1 任務目標

根據測量系統的測量原理及過程找出其中影響測量精度的誤差來源，并計算其擴展不確定度。

2 測量原理

測量系統結構如圖1所示。被測量的工件放置在載物臺上，通過各運動軸的運動自動調整物距成像。如被測工件表面有劃痕則會呈現倒三角形影像。在本測量系統中為了驗證測量系統的準確度，利用量塊人為制造階梯差得到圖2所示影像。通過計算成像后的像素點計算出兩條光帶之間的距離D，代入公式H=D×K（K為固定值，由標定得出）得到階梯的高度。

3 數學模型分析

式中：H——測量結果；

H1——儀器讀數。

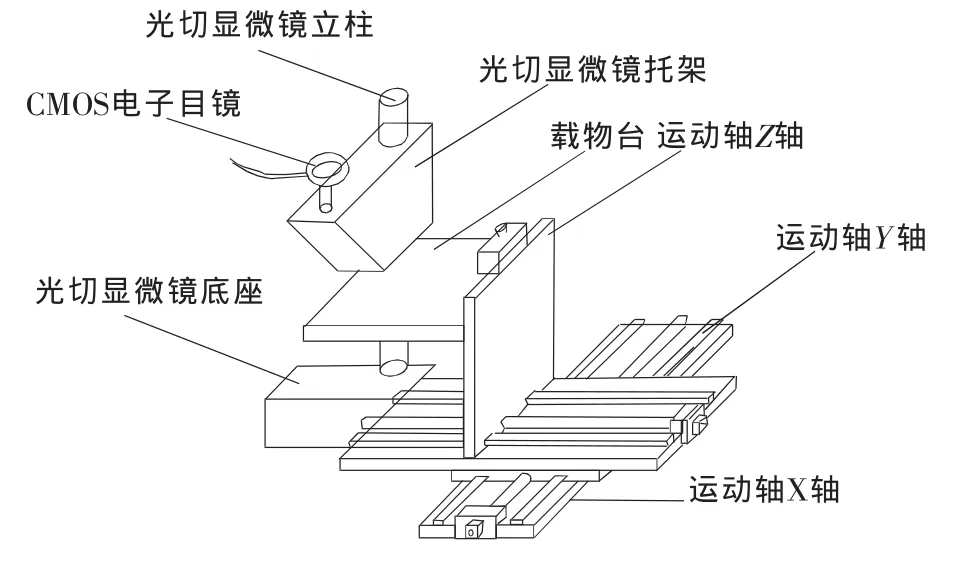
圖1 測量系統結構圖

圖2 利用量塊人為制造階梯差所得影像

4 誤差來源與標準不確定度分量分析

4.1 光切顯微鏡儀器本身誤差引入的標準不確定度分量

光切顯微鏡的機械結構無法達到完美狀態，光學鏡片的加工也無法保證透鏡焦點和鏡面曲率的準確，電子目鏡成像不可避免的發生扭曲等情況都會影像光切顯微鏡的示值誤差[2]。本測量系統的光切顯微鏡由普通光切顯微鏡改造而成，并通過計量機構校準，其示值誤差可以參考上海市計量測試技術研究院出具的“微小深度尺寸現場測量系統”檢測報告（證書號：2012D33-30-410003）中的檢測結果（截取結果部分），如表1所示。

表1 檢測結果

儀器示值誤差在測量范圍內均勻分布[3]，故取均勻分布系數b=0.58，本測量系統7倍鏡頭測量范圍最大為800μm，示值誤差為±40μm，14倍鏡頭測量范圍最大為100μm，示值誤差為±10μm。由此得到標準不確定度：

4.2 三軸工作臺自動定位引入的標準不確定度分量

本測量系統中的三軸工作臺是由伺服電機通過絲杠帶動運行，各軸的最小運行間距為0.1μm。在自動定位的過程中儀器無法每次都停留在最佳位置上，對此進行了定位實驗。在其他條件不變的情況下采取多次相鄰位置測量的方法分析其誤差，數據如表2、表3所示。

通過對以上實驗數據的觀察，可以斷定由運動軸定位引起的誤差基本呈三角分布[3]，故取均勻分布系數b=0.40。7倍物鏡定位實驗結果顯示臨近位置測量結果最大差值為3.48μm，取其半寬度為1.74μm；14倍物鏡定位實驗結果顯示臨近位置測量結果最大差值為2.82μm，取其半寬度為1.41μm由此得到標準不確定度：

表2 7倍物鏡定位實驗結果 單位：μm

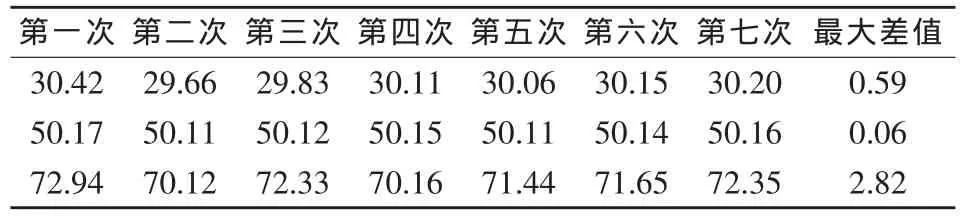
表3 14倍物鏡定位實驗結果 單位：μm

4.3 測量重復性引入的標準不確定度分量

在目前科學理論水平上，無論何種精密儀器都無法完全解析其誤差來源，對于這類暫時無法分析但又確實影響測量結果準確性的因素統一歸類為隨機誤差[3]。隨機誤差帶來的標準不確定度通常以重復性實驗得到數據，如表4所示，代入貝塞爾公式計算得到。

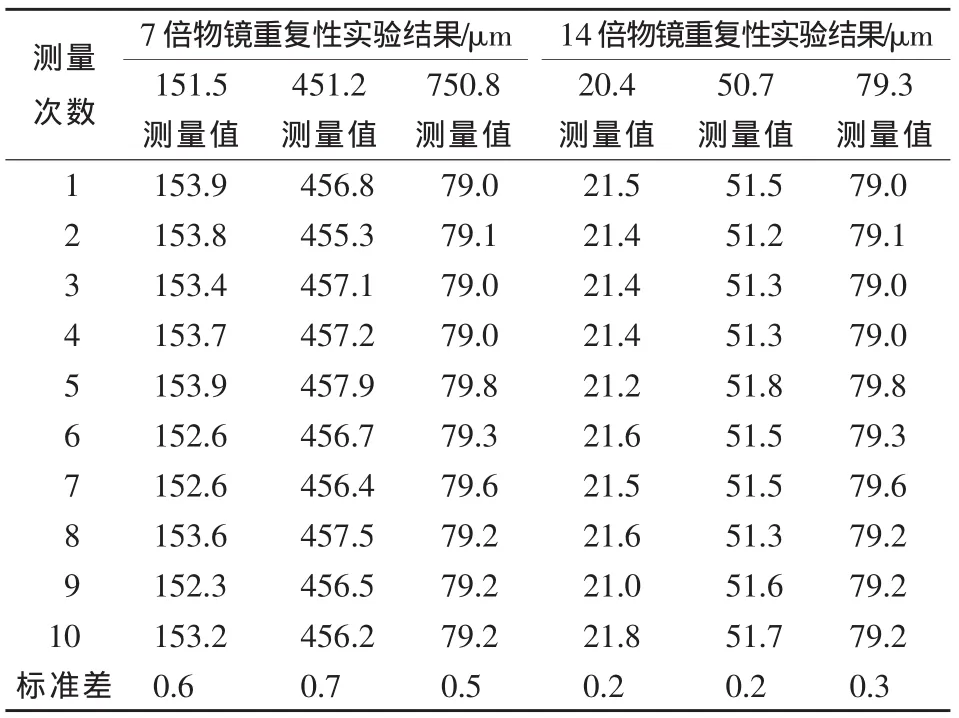
表4 測量10次數據

由此得到標準不確定度：

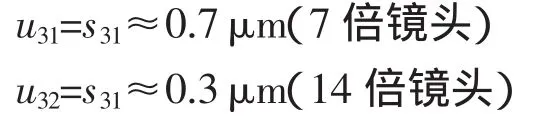
5 各標準不確定度分量相關性分析

由數學模型可知各標準不確定度分量顯然不相關。

6 合成標準不確定度

標準不確定度匯總見表5。合成標準不確定度為

表5 標準不確定度匯總表

7 擴展不確定度

取包含因子k＝2，則擴展不確定度計算結果如下

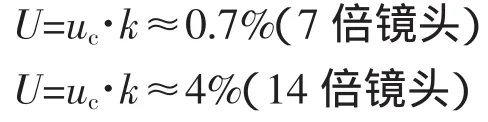
8 結束語

本文對浙江省計量科學研究院開展的“微小深度尺寸現場測量系統的研究”項目中自制的表面深度測量系統在測量微小深度時的誤差來源與不確定度進行了分析。通過本次測量不確定度的分析，得到的最終結果符合預期目標，擴展不確定度不大于10%。實驗室環境溫度為20℃，而將來該測量系統應用到現場測量時溫度將偏離20℃，會引入新的系統誤差，故本次分析暫未考慮溫度變化對測量系統測量精度變化的影響。

[1]施昌彥，宣安東.實用測量不確定度評定及案例[M].北京：中國計量出版社，2003.

[2]JJF 1092—2002光切顯微鏡校準規范[S].北京：中國計量出版社，2002.

[3]JJF 1059—2012不確定度評定與表示[S].北京：中國質檢出版社，2012.

[4]黃柳，余桂英，鄭穎君.微小深度尺寸現場測量系統的研究[J].光學技術，2011，37（5）：556-561.