要素雙重模糊下的合作博弈Shapley值的算法

趙寶福，張艷菊

遼寧工程技術大學工商管理學院，遼寧葫蘆島 125105

要素雙重模糊下的合作博弈Shapley值的算法

趙寶福，張艷菊

遼寧工程技術大學工商管理學院，遼寧葫蘆島 125105

1 前言

相比于非合作博弈研究局中人的具體結盟對策，經典的合作博弈研究的是聯盟最終形成及聯盟內部的公平收益分配。Shapley值是合作博弈理論上的一種解的表達式。

經典合作博弈存在以下兩個嚴格假設：局中人至多加入一個聯盟且局中人完全地加入某個聯盟；聯盟支付事前已知。可是在實際中，局中人有時可以以不同的參與度參加到不同的聯盟中，并且他們不同合作策略選擇下的收益也具有不確定性。為了更好地將博弈論應用到實際生活中，國內外學者展開了模糊合作博弈理論研究。

到目前為止，國內外學者主要圍繞以下兩方面進行研究：

（1）僅參與度模糊的模糊合作博弈（也稱為聯盟模糊的模糊合作博弈）。主要成果：Aubin[1]正式提出了模糊合作博弈的概念；Butnariu[2-3]對模糊Shapley值給出了定義，但是該定義未能很好地滿足現實的應用需求；Tsurumi[4]在前人研究的基礎上構造了一個具有Choquet積分的模糊Shapley值，該構造既單調非減又連續；文獻[5]將局中人的聯盟隸屬度表示為介于[0，l]區間的三角模糊數，該研究未考慮模糊被測函數下的Choquet積分計算中的一個重要問題，即不同置信水平下模糊隸屬度截集的排序問題。

（2）僅具有模糊支付的模糊合作博弈。主要成果：Mares[6-7]拓廣了原有的模糊合作博弈，指出帶有模糊支付的合作博弈也是模糊合作博弈的一種形式，按照傳統的Shapley值定義了模糊Shapley值，但是，他定義的模糊Shapley值無法滿足Shapley提出的三條公理；Aarts[8]等從集合論的角度，研究了合作博弈的Shapley值，使模糊Shapley值得到了拓展和延伸；文獻[9]利用區間數運算的性質，拓展了傳統Shapley函數滿足的三條公理，提出了聯盟支付為區間數的Shapley函數形式，該研究對本文的研究起到一定的啟發作用。

模糊合作博弈除了以上兩部分內容之外，還應包括具有模糊支付和模糊參與度的模糊合作博弈。Borkotokey[10]構建了帶模糊支付和模糊聯盟的模糊合作博弈的基礎理論框架，并對其進行了初步分析。孟凡永、張強[11]定義了模糊支付下具有Choquet積分形式的模糊合作博弈，提出了該模糊合作博弈下具有Choquet形式的Shapley值。該研究本質上是帶模糊支付的合作博弈，局中人相對于合作的隸屬度仍為實數。鄒珍珍[12]僅提出了該模糊合作博弈的思想，支付函數以及Shapley函數等問題都未提及。

綜上所述，目前對于具有模糊支付和參與度模糊的模糊合作博弈的研究只是提出了這個理念，尚未有人進行全面研究，究其原因是該研究涉及到模糊數的運算及模糊數的排序，以往基于擴張原理的模糊數的排序和運算存在遍歷性，非常復雜。本文利用模糊數學相關理論，在Choquet積分形式的基礎上，將支付函數和參與度拓展為模糊數，給出要素雙重模糊下的模糊合作博弈的定義及其Shapley值的定義。應用模糊結構元理論[13-17]，構造了要素雙重模糊下的模糊合作博弈的模糊Shapley值，使模糊Shapley值的隸屬函數得到解析表達。該研究使得模糊Shapley值的表達易操作、推廣，必將使模糊合作博弈理論在現實應用中發揮更充分的作用。

2 傳統合作博弈的Shapley值

合作博弈是局中人在競爭中為取得自己的最大利益而進行決策分析的模型。在合作博弈的過程中，局中人需要考慮如何結成聯盟及如何分配合作所取得的收益。

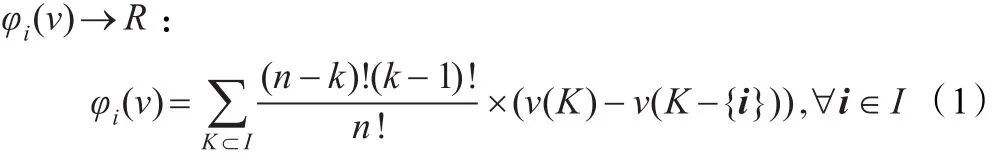
其中，k為聯盟K中的人數，n為局中人的個數。φ(ν)=(φi(ν)),i∈I，為Shapley值向量，簡稱Shapley值，它是支付函數ν的單調非減函數，在滿足超可加性的合作博弈中表示某一確定的分配。

3 基于模糊結構元的模糊數表示及模糊數排序

設E為實數域R上的模糊集，隸屬函數記為E(x)，x∈R。如果E(x)滿足下述性質：（1）E(0)=1；（2）在區間[-1，0)上E(x)是單增右連續函數，在區間（0，1]上是單降左連續函數；（3）當x＜-1或者x＞1時，E(x)=0。則稱E為R上的模糊結構元。

若模糊結構元E滿足：（1）?x∈(-1，1)，E(x)＞0；（2）E(x)連續，且在[-1，0)上嚴格單增，在（0，1]上嚴格單降，則稱E為正則的；若E(-x)=E(x)，稱E為對稱的。

定理1[15]設E是R上的任意模糊結構元，具有隸屬函數E(x)，f(x)是[-1，1]上單調有界函數，則f(E)是R上有界閉模糊數。反之，對于給定的正則模糊結構元E和任意的有界閉模糊數A~，總存在一個[-1，1]上的單調有界函數f，使得A~=f(E)，稱模糊數A~是由模糊結構元E生成的。

定理2[15]若模糊數A~=f(E)，則A~的隸屬函數為E(f-1(x))，這里f-1(x)是f(x)關于變量x和y的輪換對稱函數（若f(x)是連續嚴格單調的，則f-1(x)是f(x)的反函數）。

上述定理的證明可參見文獻[13-17]。

例如，對于三角模糊數A~=(a，b，c)，取模糊結構元E，其隸屬函數為：

定理3[15]設E是對稱模糊結構元，如果f和g是[-1，1]上兩個同序單調函數（不妨假定都是單調增函數），模糊數A=f(E)，B=g(E)，fτk是f的同序變換，則有如下結論：

（1）A和B是任意有界模糊數，則A+B=(f+g)(E)，具有隸屬函數：

模糊數可按照該定義進行比較排序，詳盡內容請見參考文獻[18]。

4 要素雙重模糊下的模糊合作博弈定義、性質及Shapley值

5 模糊Shapley值的結構元表示

證明證明過程同定理6，此處略。

6 結構元線性生成的模糊Shapley值表達式

證明證明過程同結論1，此處略。

7 算例

假設局中人a1、a2、a3三家企業欲合作一項目，如果局中人獨立完成，則a1可獲利約為100萬元，a2、a3分別可獲利約為200萬元；如果a1、a2合作、a1、a3合作分別可獲利約為600萬元，如果a2、a3合作可獲利約為800萬元，如果a1、a2、a3合作可獲利約為1 200萬元。a1、a2、a3參與該項目的參與度分別約為0.2、0.4、0.6。上述預期收益用三角模糊數表示為：

根據定理7，要素雙重模糊下的模糊合作博弈的局中人a1的Shapley值計算過程為：

8 結論

在前人提出具有模糊支付和模糊參與度概念的基礎上，本文基于Choquet積分，將支付函數和參與度拓展為模糊數，給出要素雙重模糊下的模糊合作博弈的定義和要素雙重模糊下的模糊合作博弈Shapley值的定義。應用模糊結構元理論，構造了要素雙重模糊下的模糊合作博弈的Shapley值，使模糊Shapley值的隸屬函數得到解析表達。從算例可以看出該研究使得模糊Shapley值的表達易操作、推廣，必將使模糊合作博弈理論在現實應用中發揮更充分的作用。

[1]Aubin J P.Cooperative fuzzy games[J].Mathematical Operation Research，1981，6：1-13.

[2]Butniariu D.Fuzzy games：a description of the concept[J]. Fuzzy Set and System，1978，1：181-192.

[3]Butnariu D.Stability and Shapley value for an n-persons fuzzy gaimes[J].Fuzzy Set and System，1980，4：63-72.

[4]Tsurumi M，Tanino T，Inuiguchi M.A Shapley functicn on a classofcooperativefuzzygames[J].EuropeanJournalof Operational Research，2001，129：596-618.

[5]逄金輝，陳秋萍.基于模糊機會約束的博弈聯盟收益[J].北京理工大學學報，2010，30（11）：1383-1386.

[6]Mares M.Fuzzy Shapley value[C]//Proceedings of Transactions of IPMU 2000，Madrid，2000：1368-1372.

[7]Mares M.Fuzzy cooperative games：cooperation with vague expectations[M].New York：Physica-Verlag Press，2001.

[8]Arts H，Hoede C，Funaki Y.A marginalisitc value for monotonic set games[J].International Journal of Game Theory，1997，26：97-111.

[9]于曉輝，張強.模糊合作對策的區間Shapley值[J].中國管理科學，2007，15（Z1）：76-80.

[10]Borkotokey S.Cooperative games with fuzzy coalitions and fuzzy characteristic functions[J].Fuzzy Sets and Systems，2008，159（2）：138-151.

[11]孟凡永，張強.具有Choquet積分形式的模糊合作對策[J].系統工程與電子技術，2010，32（7）：1430-1436.

[12]鄒珍珍.不完全信息模糊合作博弈特征函數研究[D].遼寧大連：大連理工大學，2011.

[13]郭嗣琮.模糊分析中的結構元方法（I）[J].遼寧工程技術大學學報，2002，21（5）：670-673.

[14]郭嗣琮.模糊分析中的結構元方法（II）[J].遼寧工程技術大學學報，2002，21（6）：808-810.

[15]郭嗣琮.模糊實數空間與[-1，1]上同序單調函數類的同胚[J].自然科學進展，2004，14（11）：1318-1321.

[16]郭嗣琮.[-1，1]上同序單調函數的同序變換群與模糊數運算[J].模糊系統與數學，2005，19（3）.

[17]Guo Sizong.Fuzzy analysis and calculate based on structured element，appliedcompuationalintelligence[C]//Proceedings of the 6th International FLINS Conference.[S.l.]：World Scientific Publishing Co Pte Ltd，2004：128-134.

[18]劉海濤，郭嗣琮.基于模糊結構元表述的模糊數排序[J].模糊系統與數學，2010，24（5）：61-67.

[19]Tsurumi M，Tanino T，Inuiguchi M.A Shapley function on a class of cooperative fuzzy games[J].European Journal of Operational Research，2001，129：596-618.

ZHAO Baofu,ZHANG Yanju

School of Business Administration,Liaoning Technical University,Huludao,Liaoning 125105,China

Considering that in the practical applications,the player can attend different league with the different participation,and they don’t sure benefits before cooperation under different cooperation strategy choice,the paper uses fuzzy mathematics theory in the traditional cooperative game.This paper expands benefits and participation as fuzzy numbers based on the Choquet integral and gives the definition of fuzzy cooperative games and fuzzy Shapley value with dual fuzzy factors.The fuzzy structured element theory is applied to analyze fuzzy cooperative games with dual fuzzy factors.The membership function of the fuzzy Shapley value can get analytic expression.An example is used to illustrate the specific application of the model.It can be seen that this method and conclusion is easy to master and promote.Fuzzy cooperative game theory can be applied more widely to real life.

cooperative games;fuzzy mathematics;Shapley value;structured element

考慮到現實應用中，局中人可能以不同的參與度參加到不同的聯盟中，并且他們在合作之前不確定不同合作策略選擇下的收益，則在傳統合作博弈中應用模糊數學理論。基于Choquet積分，將支付函數和參與度拓展為模糊數，給出要素雙重模糊下的模糊合作博弈的定義和模糊合作博弈Shapley值的定義。應用模糊結構元理論，構造了要素雙重模糊下的模糊合作博弈的Shapley值，使模糊Shapley值的隸屬函數得到解析表達。通過一個算例，來說明該模型的具體應用。可以看出，該研究方法和結論易掌握、推廣，使模糊合作博弈理論可以更廣泛地應用到現實生活中。

合作博弈；模糊數學；Shapley值；結構元

A

TP301

10.3778/j.issn.1002-8331.1306-0123

ZHAO Baofu,ZHANG Yanju.Algorithm of Shapley value for cooperative games with dual fuzzy factors.Computer Engineering and Applications,2013,49（19）：25-30.

國家自然科學基金（No.71201012）；教育部人文社會科學研究規劃基金（No.12YJC630071）；葫蘆島市科技局研究項目。

趙寶福（1957—），男，教授，博士生導師，研究方向：模糊決策理論與應用，區域經濟學股份制經濟等；張艷菊（1983—），通訊作者，女，博士研究生，研究方向：模糊決策理論與應用，區域經濟學等。E-mail：juzi2002@126.com

2013-06-12

2013-08-01

1002-8331（2013）19-0025-06

CNKI出版日期：2013-08-05http://www.cnki.net/kcms/detail/11.2127.TP.20130805.0943.002.html

◎理論研究、研發設計◎