人工魚群算法在橋梁傳感器優化配置中的應用

趙宇，彭珍瑞，殷紅

蘭州交通大學機電工程學院，蘭州 730070

人工魚群算法在橋梁傳感器優化配置中的應用

趙宇，彭珍瑞，殷紅

蘭州交通大學機電工程學院，蘭州 730070

1 引言

目前，國內外橋梁結構健康監測系統的研究與應用已取得了一定的成果與進展，傳感器子系統作為其中不可或缺的重要部分，在橋梁結構健康監測系統中為反映橋梁結構健康狀況信息的獲取奠定了基礎[1]。如何在最小的經濟投入下，使用最少的傳感器獲取最全面的信息，是一個完整橋梁健康監測系統所需解決的問題之一。黃民水[2]等人在基本遺傳算法的基礎上進行改進，提出了一種基于二重結構編碼的遺傳算法橋梁結構傳感器優化配置方法；田莉[3]等人基于自適應模擬退火遺傳算法研究了傳感器的優化配置。采用隨機類算法（如遺傳算法、模擬退火算法、粒子群算法等）來進行傳感器的優化配置，是目前研究橋梁結構健康監測傳感器優化配置的熱點，但這些算法收斂速度慢精度低，易早熟陷入局部最優。

人工魚群算法（Artificial Fish School Algorithm，AFSA）是一種基于動物行為的仿生類新型智能優化算法，模擬魚群在覓食過程中的行為，通過魚群中人工魚之間的協作達到群體最優。人工魚群算法已經在參數估計[4]、聚類分析[5]、神經網絡[6]、故障診斷[7]等方面的到了應用，并取得了較好的效果。本文采用人工魚群算法對橋梁結構健康監測傳感器進行優化配置，經比較，其結果優于粒子群算法（Particle Swarm Optimization，PSO）。

2 人工魚群算法的描述

人工魚群算法是李曉磊[8]等提出的一種基于魚類覓食、聚群、追尾、隨機等行為的群體智能優化算法。

在求解問題時，首先初始化魚群，魚群中每條人工魚是給定范圍內的隨機n維數組。設一條人工魚的當前位置為Xi=(x1，x2，…，xn)，感知范圍為Visual，某時刻所在位置在求解極小值問題中，若該時刻所在位置目標函數值Yν=f(Xν)即食物濃度低于當前位置食物濃度Yi，則人工魚向該位置前進，到達位置Xnext：

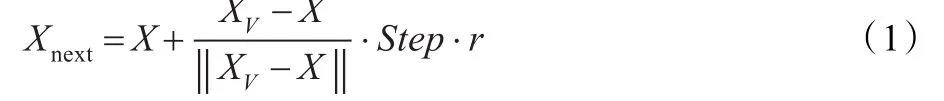
其中，r為[0，1]之間的隨機數；Step為步長。若該位置食物濃度Yν高于當前位置，則繼續對周圍環境做出巡視。人工魚群算法就是基于觀測感知范圍內其他人工魚食物濃度決定自身前進方向這種思想實現尋優過程的。

圖1 橋梁平面布局圖（單位：mm）

3 基于人工魚群算法的橋梁傳感器優化配置

3.1 橋梁傳感器優化配置數學模型

首先，建立橋梁有限元模型，進行模態分析，提取其模態振型。設橋梁有限元模態振型矩陣Φn×l，n為有限元模型節點自由度即傳感器待配置點的自由度，l為模態振型的階數。從中選取m個自由度作為傳感器最終配置點，使目標函數MAC矩陣的非對角線元達到最優，即：

橋梁傳感器優化配置作為一種典型的組合優化問題，要求使用最少的成本將傳感器配置在最合理的位置，使得傳感器所測得的信息能夠真實的反映橋梁的健康狀況，為橋梁狀態的評估提供依據。而人工魚群算法在對問題目標函數最優解的搜索過程中，有一定的自適應力，可以并行搜索，具有較強的全局優化能力。故運用人工魚群算法求解橋梁傳感器優化配置的數學模型所得的目標函數，解決了這一優化問題。

3.2 橋梁傳感器優化配置算例

本文對一座主橋（21 133.4+33 509.8+21 133.4）的拱橋[10]進行傳感器優化配置，橋面寬度8 000 mm，主要結構由梁和板材料（橋面材料厚度為12 mm）組成。橋面材料的彈性模量為E=1.6×105MPa，泊松比為0.35；其他梁材料的彈性模量為E=2.06×105MPa，泊松比為0.3。橋梁平面布局圖如圖1所示。

利用ANSYS13.0建立拱橋有限元模型，其中桁架采用BEAM188單元模擬，橋面板采用SHELL63單元模擬，有限元模型如圖2所示。對橋梁結構進行模態分析，提取前l階振型，構造模態振型矩陣Φn×l，n為節點自由度即傳感器待配置點的自由度，為了便于計算將節點自由度從小到大進行編號，假定單個節點自由度為3，則編號為1，2，…，3n。將該矩陣作為人工魚群算法解決橋梁傳感器優化配置問題的基本數據，用于求得MAC矩陣。

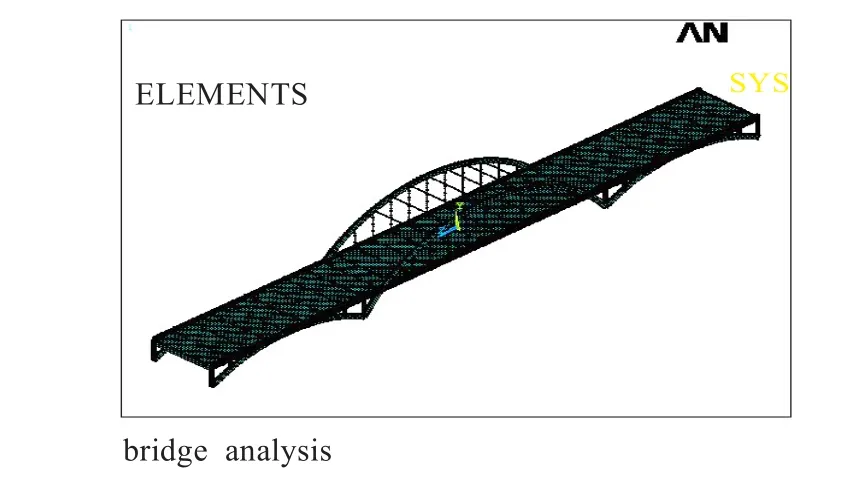
圖2 橋梁有限元模型圖

3.3 人工魚群算法在橋梁傳感器優化配置中的應用

3.3.1 人工魚群算法的三種行為

人工魚群算法主要有覓食、聚群、追尾等行為。模擬魚群趨向食物的行為，稱為覓食行為。設人工魚當前位置Xi，感知范圍內的某一位置Xj，若當前食物濃度Yi＞Yj，則向Xj方向前進一步；否則，繼續嘗試try_number次。若仍不滿足前進條件，則隨機移動一步，隨機行為就是在感知范圍內隨機的選擇移動方向。

魚類大量或少量的進行聚群行為，覓食或躲避敵害。設人工魚當前位置Xi，感知范圍內其他人工魚的數目nf，當前中心位置Xc，食物濃度Yc。若＜δYi（δ為擁擠度因子），表明當前中心位置有較多食物并且周圍不太擁擠，人工魚向當前中心位置Xc方向前進一步；否則，執行覓食行為。同時，某一條人工魚Xj，食物濃度Yj。若＜δYi，表明當前位置有較多食物并且周圍不太擁擠，人工魚向當前位置Xj方向前進一步，附近的人工魚會尾隨其后游過來，完成追尾行為；否則，執行覓食行為。

人工魚通過以上幾種行為感知周圍環境，在所對應問題中，某條人工魚表現出的狀態即為目標函數最優解。

3.3.2 人工魚群算法橋梁傳感器優化配置步驟

在人工魚群算法求解橋梁傳感器優化配置問題中，每條人工魚作為傳感器候選配置點，MAC矩陣最大非對角元最小時的人工魚所對應的點為傳感器的最終配置點。

（1）初始化魚群，針對橋梁傳感器優化配置問題，初始化魚群，人工魚群大小為N，隨機產生n行N列初始魚群，n為節點自由度即傳感器待配置點的自由度，人工魚行號與節點自由度編號相對應，每列表示一條人工魚的傳感器待配置點，每條人工魚取[0，1]范圍的隨機數。設置最大迭代次數MAXGEN，覓食行為嘗試次數try_number，感知范圍Visual，步長Step以及擁擠度因子δ。

（2）計算各條人工魚的目標函數值，根據有限元模態分析后構造的模態振型矩陣Φn×l，n為節點自由度即傳感器待配置點的自由度，按式（2）給出的目標函數，隨機選取其中m(2＜m＜n)行求得的MAC矩陣最大非對角元，m為傳感器最終配置點自由度。

（3）對人工魚群執行聚群行為、追尾行為，選擇目標函數值小的方向為移動方向，若兩種行為均不滿足前進條件，則執行覓食行為，若達到覓食行為最大嘗試次數try_number時仍不滿足前進條件，則執行隨機行為。

（4）重新計算各條人工魚的目標函數值，判斷是否達到最大迭代次數，是則繼續下一步，否則執行步驟（3）。

（5）確定最優解，即MAC矩陣最大非對角元最小時的配置點為最優解，此時傳感器最終配置點自由度m及MAC矩陣最大非對角元均為最優。

人工魚群算法流程圖如圖3所示。

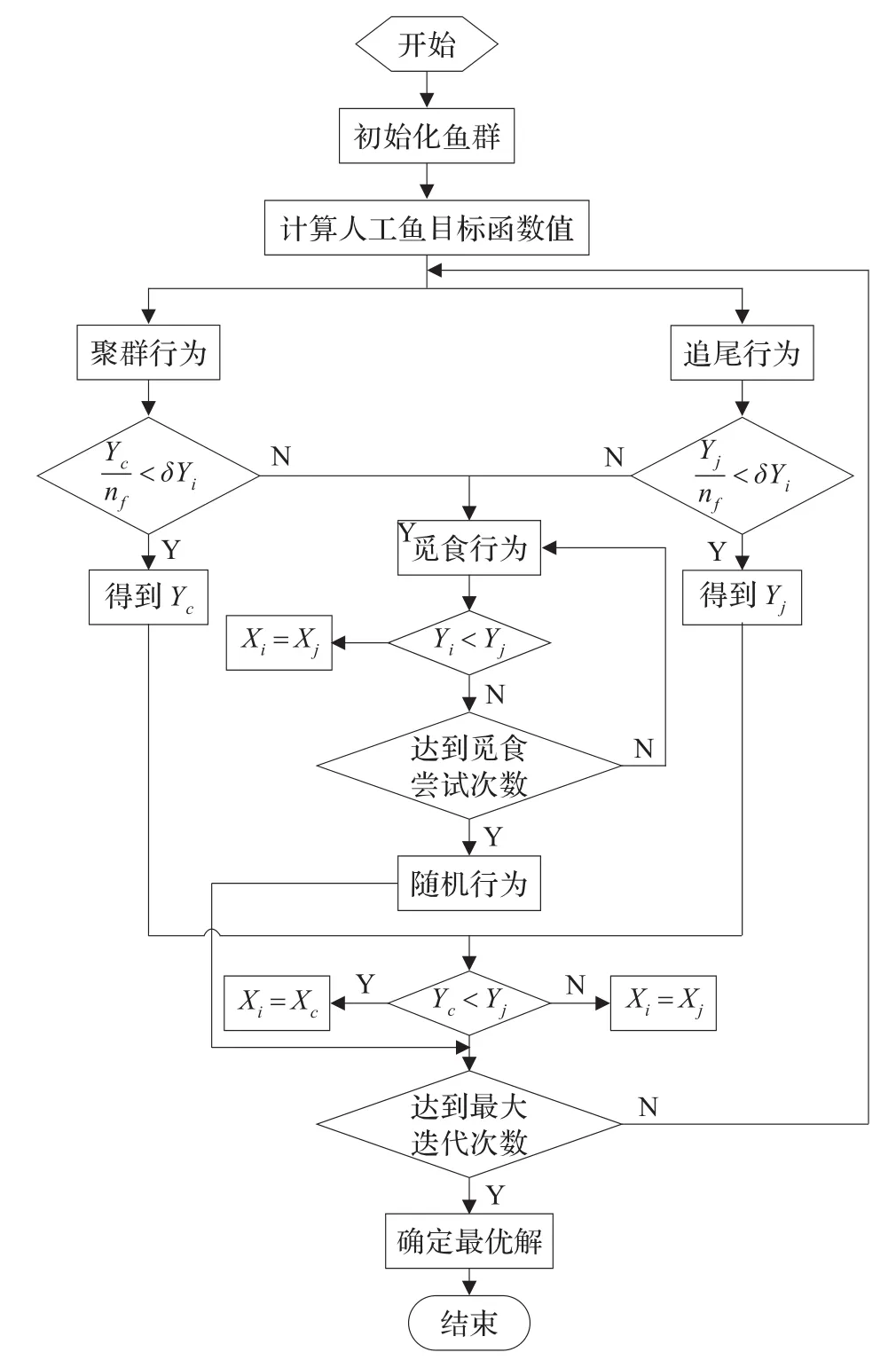
圖3 人工魚群算法流程圖

4 仿真實驗

在圖2橋梁有限元模型中，全橋共劃分12 631個單元，11 332個節點，提取模型前6階振型。選取橋面主梁與主拱拉梁及副拱立柱連接處作為傳感器候選測點，由于橋梁結構對稱，選擇橋梁1/4結構進行傳感器優化配置，其他部分參照配置。共26個節點，每個節點3個自由度，即x、y、z方向的平動，共78個自由度，模態振型矩陣Φ78×6。候選測點示意圖如圖4所示，并將節點自由度從小到大進行編號1，2，…，78。例如，節點12的3個自由度編號為1、2、3。

圖4 傳感器候選測點示意圖

4.1 人工魚群算法參數選取

根據人工魚群算法的流程，利用MATLAB R2009b編程對算例進行求解。針對參數的不同設置對橋梁結構健康監測傳感器優化配置結果的影響，通過多次實驗測試，對各參數進行調整，觀察各參數的取值對優化值（目標函數值MAC矩陣的最大非對角線元最小）的影響。初選人工魚群大小N=100，最大迭代次數MAXGEN=150，覓食行為嘗試次數try_number=5，感知范圍Visual=0.5，步長Step=0.1，擁擠度因子δ=0.5。

4.1.1 覓食行為嘗試次數try_number與優化值

人工魚群大小N、最大迭代次數MAXGEN、感知范圍Visual、步長Step、擁擠度因子δ均為初選值，對覓食行為嘗試次數try_number取不同的值，程序運行20次，它與優化值關系如圖5所示。

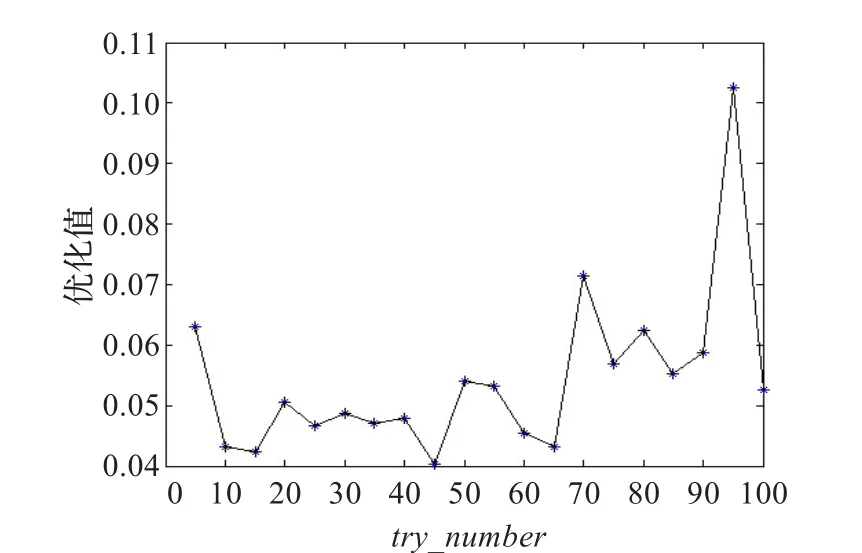
圖5 try_number與優化值關系曲線圖

從圖5來看，當try_number在10到45之間時，優化值在0.04到0.05之間且波動不大；當try_number=95時，優化值達到最大0.102 5，誤差較大。

4.1.2 擁擠度因子δ及感知范圍Visual與優化值

其他參數均為初選值，運行程序，觀察不同擁擠度因子δ及感知范圍Visual對優化值的影響，關系曲線如圖6所示。

由圖6可知，δ在0.5到2.0之間所對優化值較小，Visual在1之后，優化值在0.032到0.042之間。總體來看，當δ的取值在0.5到2.0之間，Visual為3時優化值較小，其他取值對優化值影響較大。

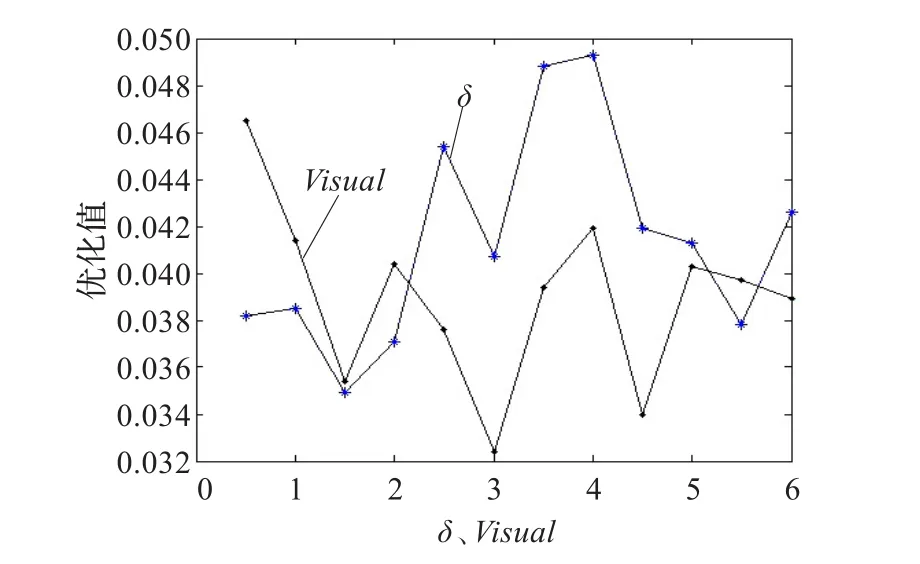
圖6 δ、Visual與優化值關系曲線圖

4.1.3 步長Step與優化值

參數選取同上，調整步長Step，測試結果如圖7所示。

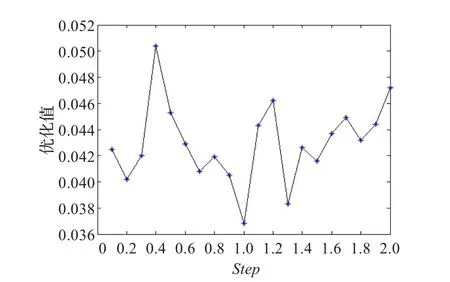
圖7 Step與優化值關系曲線圖

從測試結果可以看出，在0.1到0.4之間，隨著Step的增加，優化值會變大，但是當達到0.4以后，優化值又逐漸減小，隨后有波動，Step為1時最小，Step在1.4到2.0之間優化值變化不大。

綜合考慮各參數設置與優化值的關系，最終選取所用傳感器最少且MAC矩陣的最大非對角線元最小時所對應的參數值，參數設置如表1所示。

表1 人工魚群算法參數設置

4.2 橋梁傳感器優化配置

根據以上參數設置運行程序，從78個自由度選擇m(2＜m＜78)個自由度配置傳感器，各自由度所對應MAC矩陣的最大非對角線元，如圖8所示。自由度在2到10之間MAC矩陣的最大非對角線元迅速減小，10到20之間其值平穩，自由度在20以后緩慢增大。當自由度為10時，可達到傳感器配置要求（MAC矩陣的非對角線元越接近于0越好），MAC矩陣的最大非對角線元為0.029 5，故所選傳感器數目為10個。傳感器配置方案如表2所示。

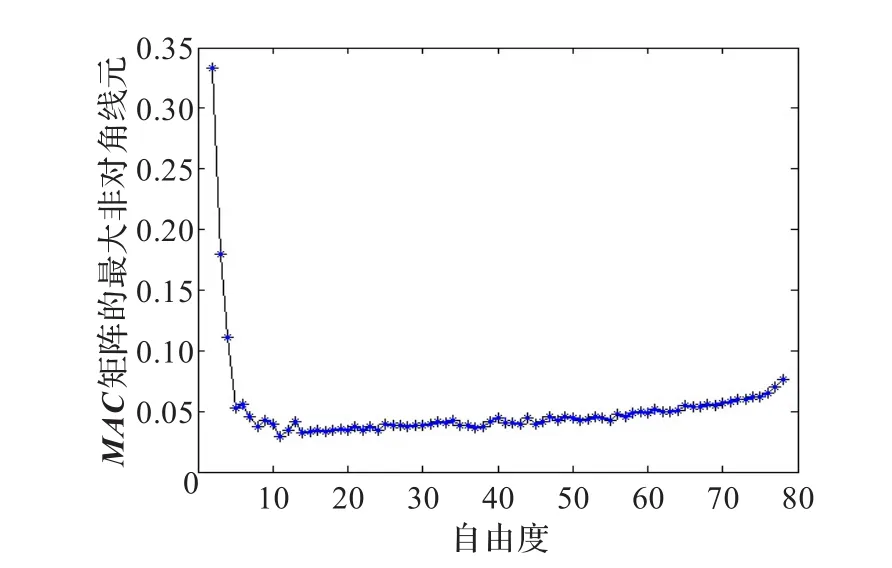
圖8 MAC矩陣的最大非對角線元變化曲線圖

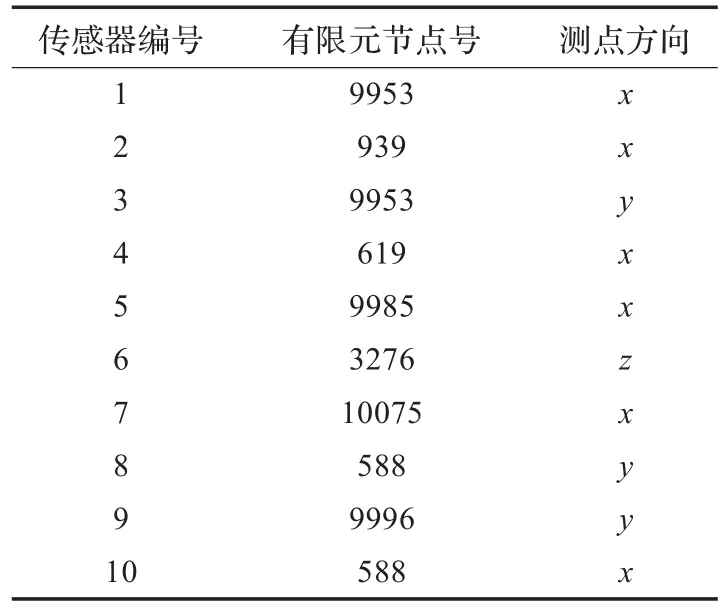
表2 傳感器配置方案

4.3 結果對比

為了評價基于人工魚群算法的橋梁傳感器優化配置方法的優劣，將人工魚群算法與基于粒子群算法的傳感器優化配置方法進行比較，收斂對比曲線如圖9所示。

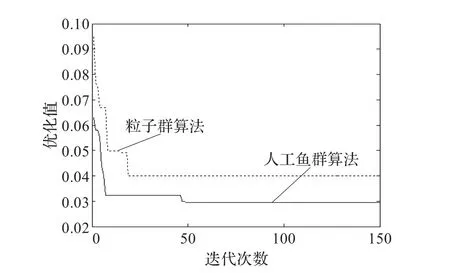
圖9 人工魚群算法與粒子群算法收斂曲線對比圖

由圖9可以看出，在第1到7次迭代過程中，人工魚群算法快速收斂到0.033 0，隨后繼續收斂且在第48次迭代后達到傳感器配置要求（MAC矩陣的最大非對角線元為0.029 5），而粒子群算法得到的MAC矩陣的最大非對角線元為0.040 0。人工魚群算法迭代速度稍慢于粒子群算法，但人工魚群算法自適應能力強，收斂精度高，克服了一般算法過早收斂陷入局部最優的問題，可以實現橋梁結構健康監測傳感器優化配置。

5 結論

本文提出了針對橋梁結構健康監測傳感器優化配置問題的人工魚群算法。為了更好地實現算法在該問題中的應用，通過多次實驗測試觀察各參數對算法性能的影響，最終選取傳感器配置最優的參數設置，提高了人工魚群算法求解橋梁傳感器優化配置問題的精度，實現了人工魚群算法在組合優化問題上的又一應用。

[1]李愛群，繆長青.橋梁結構健康監測[M].北京：人民交通出版社，2009：157-173.

[2]黃民水，朱宏平，李煒明.基于改進遺傳算法的橋梁結構傳感器優化布置[J].振動與沖擊，2008，27（3）：82-87.

[3]田莉，陳換過，祝俊，等.基于自適應模擬退火遺傳算法的傳感器優化配置研究[J].振動工程學報，2012，25（3）：238-243.

[4]李曉磊，薛云燦，路飛，等.基于人工魚群算法的參數估計方法[J].山東大學學報：工學版，2004，34（3）：84-87.

[5]蘇錦旗，吳慧欣，薛惠鋒.基于人工魚群算法的聚類挖掘[J].計算機仿真，2009，26（2）：147-150.

[6]張穎.基于改進魚群算法的BP神經網絡優化設計[D].廣州：華南理工大學，2012.

[7]陳安華，周博，張會福，等.基于改進人工魚群算法的機械故障聚類診斷方法[J].振動與沖擊，2012，31（17）：145-148.

[8]李曉磊，邵之江，錢積新.一種基于動物自治體的尋優模式：魚群算法[J].系統工程理論與實踐，2002，22（11）：32-38.

[9]劉寒冰，吳春利，程永春.不同適應度函數的遺傳算法在橋梁結構傳感器布設中的應用[J].吉林大學學報：工學版，2012，42（1）：51-56.

[10]涂振飛.ANSYS有限元分析工程應用實例教程[M].北京：中國建筑工業出版社，2010：83-94.

[11]吳月萍，杜奕.改進的人工魚群算法的參數分析[J].計算機工程與應用，2012，48（13）：48-52.

[12]Kammer D C.Sensor placement for on orbit modal identification of large space structures[J].Journal of Guidance，Control，and Dynamics，1991，14（2）：252-259.

[13]Li D S，Li H N，Fritzen C P.The connection between effective independence and modal kinetic energy methods for sensor placement[J].Journal of Sound and Vibration，2007，305（4/5）：945-955.

[14]路楊，張曉麗.CW-PSO及其在古建筑傳感器優化配置中的應用研究[J].計算機工程與應用，2013，49（5）：268-270.

[15]林賢坤，覃柏英.微粒算法在傳感器優化配置中的應用[J].控制工程，2013，20（1）：84-92.

ZHAO Yu,PENG Zhenrui,YIN Hong

School of Mechatronics Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China

In order to achieve optimal sensor placement for bridge structural health monitoring,using less sensors gain as many as information reflect health status of bridges structural,artificial fish school algorithm is applied in an arch bridge,to solve optimal sensor placement problem for bridge with three typical behaviors of artificial fish.The results show that artificial fish school algorithm has high self-adaptive ability and precision,can achieve optimal sensor placement for bridge structural health monitoring.

artificial fish school algorithm;optimal sensor placement;bridge structural health monitoring

為了實現橋梁結構健康監測傳感器的優化配置，用盡可能少的傳感器獲取盡可能多的反映橋梁結構健康狀況的信息，將人工魚群算法應用于一座拱橋的傳感器配置中，利用人工魚的三種典型行為，解決橋梁傳感器優化配置問題。結果表明，人工魚群算法自適應能力強，收斂精度高，可以實現橋梁結構健康監測傳感器優化配置。

人工魚群算法；傳感器優化配置；橋梁結構健康監測

A

TP18

10.3778/j.issn.1002-8331.1305-0063

ZHAO Yu,PENG Zhenrui,YIN Hong.Optimal sensor placement for bridge structural health monitoring based on artificial fish school algorithm.Computer Engineering and Applications,2013,49（19）：260-264.

趙宇（1990—），女，碩士研究生，主要研究方向為智能算法橋梁結構健康監測；彭珍瑞（1972—），男，博士，教授；殷紅（1978—），女，博士研究生，副教授。E-mail：zhaoyulzjtu@163.com

2013-05-09

2013-07-22

1002-8331（2013）19-0260-05